基于网络可控性的城市轨道交通客流网络限流优化控制方法
2018-05-07曾璐,刘军,秦勇,王莉,4
曾 璐,刘 军,秦 勇,王 莉,4
(1.北京交通大学 交通运输学院,北京 100044;2.江西理工大学 应用科学学院,江西 赣州 341000;3.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044;4.北京市城市交通信息智能感知与服务工程技术研究中心,北京 100044)
近些年城市轨道交通客流量迅猛增长,尤其是早晚高峰时段客流拥挤现象十分严重,给轨道交通的运营安全提出严峻挑战。随着城市轨道交通网络一体化运营,传统的客流控制方法无法适应其大运量、线网密集、组织关系复杂等特点。从城市轨道交通客流网络可控性角度优化限流车站及策略为网络控流提供了新的视角。
由于城市轨道交通客流量的持续攀升,城市轨道交通客流控制相关问题研究引起了众多学者的关注。文献[1]以上车总人数最多和各站上车比例方差最小为目标,构建城市轨道交通系统的单线多站协同客流控制模型。文献[2-3]基于排队网络理论分析车站能力与需求匹配情况,给出单车站限流方法。在单站能力评估分析的基础上构建单线多站协同限流模型。文献[4]以网络客流需求及其分布特点为研究基础,建立以乘客延误最小化及客流需求与运能配度最大化的客流控制模型。文献[5]在考虑网络容量约束条件下,提出网络流入客流调控模型并进行求解。文献[6]针对Bus bunching问题,构建使公交车辆在行驶过程中延迟时间达到最小的数学规划模型。综上,城轨控流的研究由单个车站向单线发展,再由多线协同向网络发展的趋势。目前的研究重点主要是单线协同限流或者局部线网建立微观模型提供限流措施,从系统的角度考虑路网整体稳定性优化限流方案的研究较少。
网络可控性的研究起步较晚,其主要研究方法分为蜂拥控制、牵引控制和结构控制三类。蜂拥控制研究多基于文献[7]提出的Boid模型。文献[8-9]将牵引控制与蜂拥控制集合应用于无标度动态网络中。文献[10]研究有向复杂动态网络的能控性。文献[11]进一步提出网络可控性判据和驱动节点的匹配方法。文献[12-15]将驱动节点的概念延伸到驱动边。文献[16-17]计算出级联失效或者网络出现扰动情况下的驱动节点数量。文献[18]研究铁路列车服务网的可控性,构建改进的LB模型。目前关于网络可控性的研究多基于复杂网络的一般特性,集中于复杂拓扑特性的分析,没有对网络的优化提出具体的控制策略,并且多数还是回归到物理拓扑链接而忽略了实际网络中节点和边权等功能属性,尚无法针对具体问题提出有效的控制方法和应对策略。
本文对城市轨道交通客流网络的拓扑结构特性进行分析,在传统控制理论的基础上构建城市轨道交通客流网的可控模型,针对不可控网络运用改进的可控性判定方法计算出可控客流网所需的最小驱动节点数量。提出基于驱动节点匹配的限流车站优化方法,给出客流网可控条件下的具体限流车站集合,并结合北京城市轨道交通网络的实际客流数据对模型及方法进行验证。
1 城市轨道交通客流网络模型构建
通过对城市轨道交通网络拓扑结构特性与客流特征的分析,本文将重点探讨城市轨道交通客流网络限流优化控制方法。
首先,基于网络客流的扩展与分布,在城市轨道交通物理网的基础上加载客流,形成基于驱动节点的城市轨道交通客流网。其次,基于系统可控判定理论,提出城市轨道交通客流网可控性判定方法,对当前实际现场的限流车站集合判断是否可控。最后,基于网络结构优化图方法,建立基于驱动节点匹配的限流车站优化方法,实现对城市轨道交通客流网络限流车站的优化控制。在实际限流过程中,随着车站实施限流措施,客流量可能会出现次高峰客流。该限流优化控制方法可根据客流状态或者时间周期进行迭代计算,得到不同时间段内的限流车站集合。当客流趋于相对稳定时,限流车站也趋于固定。
1.1 城市轨道交通客流网络模型
将车站定义为点,连接两个车站的轨道定义为边,构成城市轨道交通物理网。在物理网基础上叠加客流分布与转移状态,将其扩展为轨道交通客流网。将车站定义为网络中的节点,如果两个车站之间有客流转移,则这两个车站之间存在边连接,转移的客流量为边的权重,这样构成的网络为城市轨道交通客流网。
1.2 限流车站备选集评价指标
由于客流具有强流动性,单从车站当前聚集的客流人数判断限流节点,无法实现面向全路网的有效控制。因此本文构建城市轨道交通客流网的基本统计指标,可从路网可达性、客流强度、局部连接密集性和客流换乘便捷性等角度生成限流车站备选集。
(1)度:节点度Ki定义为节点i与其他节点的连接个数。
( 1 )
式中:nij为0-1变量,表示节点i和j之间的连接关系。
城市轨道交通客流网的度值反映了网络节点的可达性。度值越大代表该车站换乘线路选择越多,换乘也越方便;反之度值越小代表该车站可达性较弱,乘客可能需要经过多次换乘才可到达目的地。
(2)节点强度:节点i和j相连接权重为wij,网络节点i强度Si定义为
( 2 )
节点强度为该节点边权重的和。城市轨道交通客流网的节点强度反映该车站的客流需求,节点强度大说明该车站的客流量大。
(3)聚集系数:反映节点在网络中的聚集程度。假设节点i和它相连接的边共有ki个,ki个节点最多有ki(ki-1)/2条边,那么ki真实存在的边数Ei与ki(ki-1)/2的比值定义为节点i的聚集系数Ci。
( 3 )
城市轨道交通客流网的聚集系数反映了车站间客流转移连接的紧密程度,聚集系数越大,说明有客流转移的车站节点与附近各个节点的连接紧密度越高。
(4)网络平均路径长度:节点i和j间的距离dij指两节点间的最短路径的边数。网络平均路径长度L定义为
( 4 )
式中:N为网络中节点的个数。
城市轨道交通客流网的平均路径长度反映了客流网中的乘客从出发地到目的地所经过的车站个数,是一个表示城市轨道交通客流网连通性的指标。
根据以上网络特性指标,构建客流网中限流车站集合备选集综合指标函数
y=α1K+α2S+α3C+α4L
( 5 )
式中:α1,α2,α3,α4为各指标参数,且α1+α2+α3+α4=1。
2 城市轨道交通客流网络可控性判定方法
2.1 城市轨道交通客流网络可控分析
轨道交通成网运营后,客流量增加,乘客换乘机会增大,客流变化规律也更加复杂。城市轨道交通客流网络是一个控制系统,外界实施的控流措施为输入,网络系统内OD客流量为状态变量。在常态或平峰情况下,城市轨道交通客流网络属于可控的范围。但在早晚高峰或大客流情况下,由于路段服务水平相对降低,客流量与区间能力不匹配,整个网络客流属于非均衡状态,即为不可控状态。这时,需要采取相应的控流措施降低路网客流聚集程度,使系统处在可控状态。
在统计时段t+Δt内,线路l任意车站i的站内人数Pi(t+Δt)可以看作其上一个统计时段的站内人数加上进出站人数之差和换入换出人数之差,其表达式为
Pi(t+Δt)=Pi(t)+Ai(t)-Di(t)+Ii(t)-Oi(t)∀t>0
( 6 )
式中:Pi(t)为t时段内i站的客流量;Ai(t)为t时段内i站的进站客流量;Di(t)为t时段内i站的出站客流量;Ii(t)为其他车站在t时段内流入i车站的客流量;Oi(t)为i车站在t时段内流出到其他车站的客流量。
客流控制主要是对进站客流量和站内客流量进行控制,虽然未从根本上减少客流需求,但是使客流需求在时间分布上予以调节,全网客流量在时间和空间分布上达到相对稳定的一个状态。减少路网客流拥挤风险,提高运营可靠性,保障系统处于最佳运输能力。
2.2 城市轨道交通客流网络可控判定方法
根据城市轨道交通客流网络拓扑结构和客流特点,构建的城市轨道交通客流网络可控模型为

( 7 )
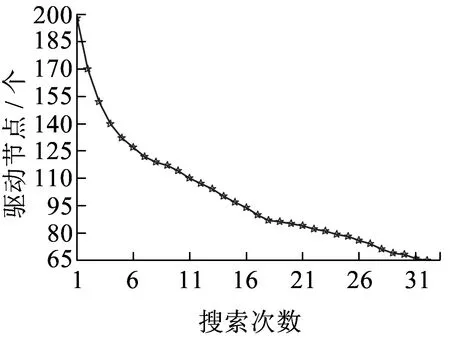
式中:aij(t)为t时段状态矩阵a的元素,j为起始车站,i为目的车站。aij(t)表示t时段从j车站到i车站的客流量的取值,Iij(t)为t时段j车站到i车站实际客流量,当Iij(t)>k时,aij=1;当Iij(t) 对文献[19]和文献[20]进行对比分析,将单个设施设备划分为4个等级,分别为A、B、C、D,它们的拥挤程度依次降低。依据北京市城市轨道交通车站拥挤风险评价标准,按照严重拥挤、拥挤、受限和畅通的评价个数情况,将车站拥挤风险等级划分为高风险、较高风险、一般风险和无风险。考虑到设备设施受限和畅通状态情况对乘客出行和车站运营影响不大,不作为划分风险等级的依据。因此整个车站的拥挤程度可由站台、通道、安检口、上行及下行楼梯以及进站口等多个调查点统计获得,具体原则见表1。 表1 车站拥挤风险总体评价表 根据车站拥挤风险总体评价结果,针对不同的级别,xi(t)分别取值为1、2、3、4;bij(t)为t时段输入矩阵b的元素,当该车站实行了限流措施,bij(t)=1,否则bij(t)=0;uj(t)为t时段第j个车站的控流强度,∀uj(t)∈[0,1]。车站控流强度表示单位时间内限制进入车站的客流量与实际客流需求量的比值,控流率越大控流强度越大。 由Kalman可控性秩判定条件,城市轨道交通客流网可控性的判定模型为 c=[baba2b…an-1b] ( 8 ) 式中:c为可控矩阵。 根据Kalman可控判定方法,当rank(c)=n时,城市轨道交通客流网为可控;当rank(c) 城市轨道交通客流网可控判定模型属于线性定常系统模型,又称为线性时不变系统,满足线性(即可叠加性)与时不变性。将客流网络实施限流控制的时间段进行细分,在细分的时间段内,客流网络的拓扑链接是不变的(即系统的参数不随时间而变化)。系统输入为实施限流的车站集合,而网络的状态(是否可控)则是由这些车站实施限流后共同作用的结果。从系统模型角度分析,本文建立客流网络可控模型中,客流网的输入为bij(t),表示是否实施限流措施,整个网络是否可控的输出也是由所有输入信号bij(t)共同决定的。因此本文所研究的客流网限流优化问题满足线性时不变性。 在网络控制中,将网络结构可控与图论相结合,从边和点匹配的方法判断网络是否可控。文献[11]提出了一种最少驱动节点ND的方法控制网络,实验结果表明驱动节点的数量主要是由网络度分布决定的。稀疏的异质型网络往往更难控制,稠密的同质型网络则需要少数的驱动节点即可控制。如图1所示,通过给定输入信号u1、u2和u3,如果系统是可控的,输入信号可以通过所有的路径到达所有的节点。 图1 可控网络原理 确定一个有向网络最少外界输入的问题则可以转化为求解该网络的最大匹配问题,如图2所示。根据左边的系统结构图,将节点与节点之间的边与方程中的状态矩阵A对应,输入信号构成输入矩阵B。在此结构系统中,当给定一个输入信号u1时,可算出方程结果是不满秩,即系统不可控。 图2 系统结构不可控 由最大匹配原则可得,匹配的点、边为红色,不匹配的点、边为绿色,如图3(a)所示。不匹配的点为驱动节点,对驱动节点给定两个输入信号u1,u2时,通过最大匹配原理得系统可控,如图3(b)所示,同理可通过上述方程计算验证。 图3 系统结构可控 本文的客流网驱动节点匹配方法是在文献[21]算法上进行改进的。如果全网的所有边都没有共享头节点或尾节点,则称全网达到最大匹配。假如没有完全匹配,驱动节点的值ND等于非匹配的节点数,对非匹配的节点给定输入信号可达所有的匹配点即可控制全网。即使选取不同的初始搜索匹配边,最终得到的最小驱动节点的个数都是固定的。对于轨道交通客流网络而言,辨识早晚高峰需要限流车站可转化为优化客流网的驱动节点,使得网络处于可控状态。 在上述算法基础上,本文针对城市轨道交通客流网络拓扑结构和客流特性,提出了基于驱动节点匹配的限流车站优化方法,具体如下: 步骤1选取某一初始匹配边Ei。若V中的所有顶点都被M匹配,则表明M为一个完全匹配,返回,说明网络当前处于可控状态;否则,以所有未匹配顶点为源点进行一次广度优先搜索,标记各个点到源点的距离。 步骤6如果当前驱动节点数量ND′>minND,删除客流量大于等于Q小于(Q+d1)的头节点,以客流量差为d1逐次迭代删除;删除进站客流量小于W人的节点,以客流量差d2进行迭代删除;直到ND′=minND,生成新的限流车站集合。 上述搜索过程是以t为一个周期,随着限流策略的实施和客流量的减少,可以重复上述过程,减少或更换限流节点,形成次高峰条件下的限流方案。 截至2015年12月26日,北京城市轨道交通共有18条运营线路(包括17条地铁线路和1条机场线),去除未开通、2号和3号航站楼的车站拥有315座车站(包括重复计算换乘站),不包括重复计算的车站为269座。以北京城市轨道交通全网为例,首先构建一个基础数据库,如图4所示。 对全网上的每一个车站按线进行编号,例如1号线:苹果园0101,古城0102,八角游乐园0103,八宝山0104,玉泉路0105,五棵松0106……。2号线:西直门0201,车公庄0202,阜城门0203……。车站编号的前两位是线路编号,后两位是这个车站所在线路的编号,见表2。 表2 北京市轨道交通路网各线路、车站编号 表2(续) 节点与节点之间的边是有方向的,方向为客流的输送方向。本案例使用2015年12月14日北京市轨道交通路网客早高峰客流数据。依据区间基础数据及客流OD数据可得到状态矩阵a为一个18 860×18 860的矩阵。 ( 9 ) 根据平峰时的OD数据对比,我们选取的阈值k为69。矩阵可转变为 (10) 矩阵b是由控流车站构成的输入矩阵,各线实际限流车站见表3。由于验证的客流数据是早高峰,所以限流车站中去除五道口、亮马桥、三元桥、金台夕照、朝阳门、复兴门、永安里、丰台科技园和动物园,因为这些站都是晚高峰实行限流车站。矩阵b即变换为一个由0和1构成的18 860×62的矩阵。 (11) 表3 2015年北京城市轨道交通限流车站 续表3 通过Kalman可控性秩判定条件计算可得,rank(c)=12 365,说明系统是不可控的。城市轨道交通网存在数量较多的换乘站点。由于存在2条甚至更多的线路通过换乘车站,根据最大匹配理论,换乘站节点周围不匹配节点较多,驱动节点数量不够,所以网络不可控。 运用3.2节提出的基于驱动节点匹配的限流车站优化方法对不可控的客流网进行优化,可得早高峰时所需的驱动节点与节点比例关系如图5所示。 图5 可控的客流网驱动节点与节点比例关系 从图5可知,驱动节点与网络节点总数的比例趋于线性分布。当驱动节点个数占节点总数25.3%,即驱动节点个数为65时,北京城市轨道交通早高峰客流网即为可控。从网络可控性角度,建议北京城市轨道交通增加采取限流车站的数量,提高其可控性,改进目前控流组织策略。 通过对城市轨道交通客流网络特性与限流车站驱动节点搜索的相关性分析得出,度阈值P取值为4,客流阈值Q取值为69,进站客流量阈值W为50,时间周期t为15 min,转移客流量差值d1取值为5,进站客流量差值d2取值为3。客流网中限流车站集合备选集综合指标函数的参数为α1=0.31,α2=0.38,α3=0.19和α4=0.12 。最小驱动节点集合搜索删除节点过程趋势如图6所示。 图6 删除驱动节点趋势 从删除驱动节点趋势图中发现整个趋势是先急后缓的,大部分车站的客流量并没有达到最小阈值,所以在前几个步骤中删除的车站数量比较多。在整个删除过程中尽量保留原有限流车站。更新的北京城市轨道交通限流车站拓扑图如图7所示。 图7 网络可控条件下北京城市轨道交通限流车站分布 图7中3个红色节点为新增加的限流车站,分别是建国门、崇文门和西直门。2个蓝色节点为删除的原有限流车站。新增的限流车站都是度为4或5的换乘站,本身客流量就比较大,车站内部结构也比较复杂。其中西直门是3条线路的换乘站,客流转移情况复杂,可在站厅内或者安检处实行限流措施。重复采用本文提出的方法,当限流措施实施4个时间周期后,在系统可控的条件下限流车站可减少2个,分别是大屯路东和天坛东门。 目前的控流方法都是经验限流,而且限流车站在同一时间段基本上固定不变。随着限流措施的实施某些车站客流量除了减少外,可能会出现次高峰状态,限流车站及限流措施的实施应该是一个动态变化的过程,因此限流车站的选取及限流时间的控制也应该是时变的。 本文基于状态空间方程和驱动节点匹配算法,从网络可控的角度研究了城市轨道交通限流优化控制方法,并结合北京轨道交通网络分析了其优化控制的特点。 (1)依据结构可控模型,构建城市轨道交通客流网络可控性判定方法,以北京城市轨道交通客流网为例验证了网络可控性理论。通过对城市轨道交通客流网络可控性的分析,结果表明在客流高峰状态下客流网是不可控的。当控流车站达到车站总数25.3%以上时,可使客流网达到可控状态。 (2)针对目前早高峰大客流网路不可控的情况,建立基于驱动节点匹配的限流车站优化方法。通过智能搜索算法识别出最小驱动节点集合,给出客流网达到可控所需的具体限流车站。 本文的可控研究方法是宏观分析全网可控状态以及驱动节点与可控性之间关系的基础理论。从大规模网络整体可控性角度出发,提出大客流条件下城市轨道交通限流车站的优化方法,规避当前研究方法多关注于单个车站或者局部区域的限流控制的缺点,更适用于运营组织关系愈加复杂的客流网络的整体优化。但本文并未涉及具体的限流措施,为了保障城市轨道交通系统的安全高效运营,在限流车站优化的基础上,如何确定限流强度和措施,实现宏观系统和微观个体的协同优化控制是未来重要的研究内容。 参考文献: [1]姜曼. 城市轨道交通单线多站协同客流控制研究[D].北京:北京交通大学, 2014:44-54 [2]XU X Y, LIU J, LI H Y, et al. Analysis of Subway Station Capacity with the Use of Queueing Theory[J]. Transportation Research Part C:Emerging Technologies, 2014,38(1): 28-43. [3]许心越. 城市轨道交通车站服务能力计算与能力适应性评估[D].北京:北京交通大学, 2015. [4]姚向明,赵鹏,乔珂,等. 城市轨道交通网络客流协同控制模型[J]. 中南大学学报, 2015,46(1): 342-350. YAO Xiangming, ZHAO Peng, QIAO Ke, et al. Modeling on Coordinated Passenger Inflow Control for Urban Rail Transit Network[J]. Journal of Central South University,2015,46(1): 342-350. [5]GUO J Y, JIA L M, QIN Y, et al. Cooperative Passenger Inflow Control in Urban Mass Transit Network with Constraint on Capacity of Station[J]. Discrete Dynamics in Nature and Society, 2015(5):1-7. [6]FELIPE D, JUAN C M, RICARDO G. How Much Can Holding and/or Limiting Boarding Improve Transit Performance?[J]. Transportation Research Part B, 2012, 46(9):1202-1217. [7]REYNOLDS C W. Flocks, Herds, and Schools: a Distributed Behavioral Model[J]. Computer Graphics, 1987,21(4):25-34. [8]WANG X F, CHEN G R. Pinning Control of Scale-free Dynamical Networks[J].Physical A: Statistical Mechanics and Its Applications,2002,310(3/4):521-531. [9]汪小帆, 苏厚胜. 复杂动态网络控制研究进展[J]. 力学进展, 2008, 38(6): 751-765. WANG Xiaofan, SU Housheng. Recent Progress in Control of Complex Dynamical Networks[J]. Advances in Mechanics, 2008, 38(6): 751-765. [10]陈关荣. 复杂动态网络环境下控制理论遇到的问题与挑战[J]. 自动化学报, 2013, 39(4): 312-321. CHEN Guanrong. Problems and Challenges in Control Theory under Complex Dynamical Network Environments[J]. Acta Automatica Sinica,2013, 39(4): 312-321. [11]LIU Y Y, SLOTINE J J, BARABSI A L. Controllability of Complex Networks[J].Nature, 2011, 473(7346):167-173. [12]YAN G, REN J, LAI Y C, et al. Controlling Complex Networks: How Much Energy Is Needed?[J]. Physical Review Letters,2012,108(21):218703. [13] NEPUSZ T, VICSEK T. Controlling Edge Dynamics in Complex Networks[J]. Nature Physics,2012,8(7):568-573. [14]FERRARINI A. Some Thoughts on the Control of Network System[J]. Network Biology, 2011,1(3/4): 186-188. [15]LOMBARDI A, HÖRNQUIST M. Controllability Analysis of Networks[J]. Physical Review E, 2007, 75(5): 56110. [16]CHEN S M, XU Y F, NIE S. Robustness of Network Controllability in Cascading Failure[J].Physical A: Statistical Mechanics and Its Applications, 2017, 471: 536-539. [17]PANG S P, HAO F. Optimizing Controllability of Edge Dynamics in Complex Networks by Perturbing Network Structure[J].Physical A: Statistical Mechanics and Its Applications,2017,470:217-227. [18]MENG X L, XIANG W L, WANG L. Controllability of Train Service Network[J].Mathematical Problems in Engineering, 2015(4):1-8. [19]北京市规划委员会. GB 50157—2013地铁设计规范[S]. 北京: 中国建筑工业出版社, 2014. [20]美国交通运输研究委员会. 公共交通通行能力和服务质量手册[M]. 2版. 杨晓光, 腾靖, 等译. 北京: 中国建筑工业出版社, 2010: 321-330. [21]HOPCROFT J E, KARP R M. An n5/2Algorithm for Maximum Matchings in Bipartite Graphs [J].SIAM Journal on Computing, 1973,2(4):225-231.
3 城市轨道交通客流网络限流车站优化方法
3.1 网络结构优化图方法
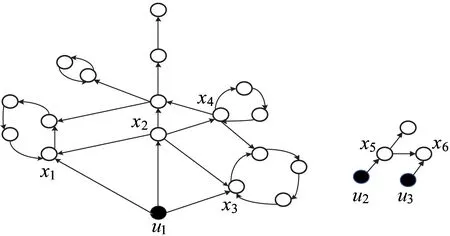

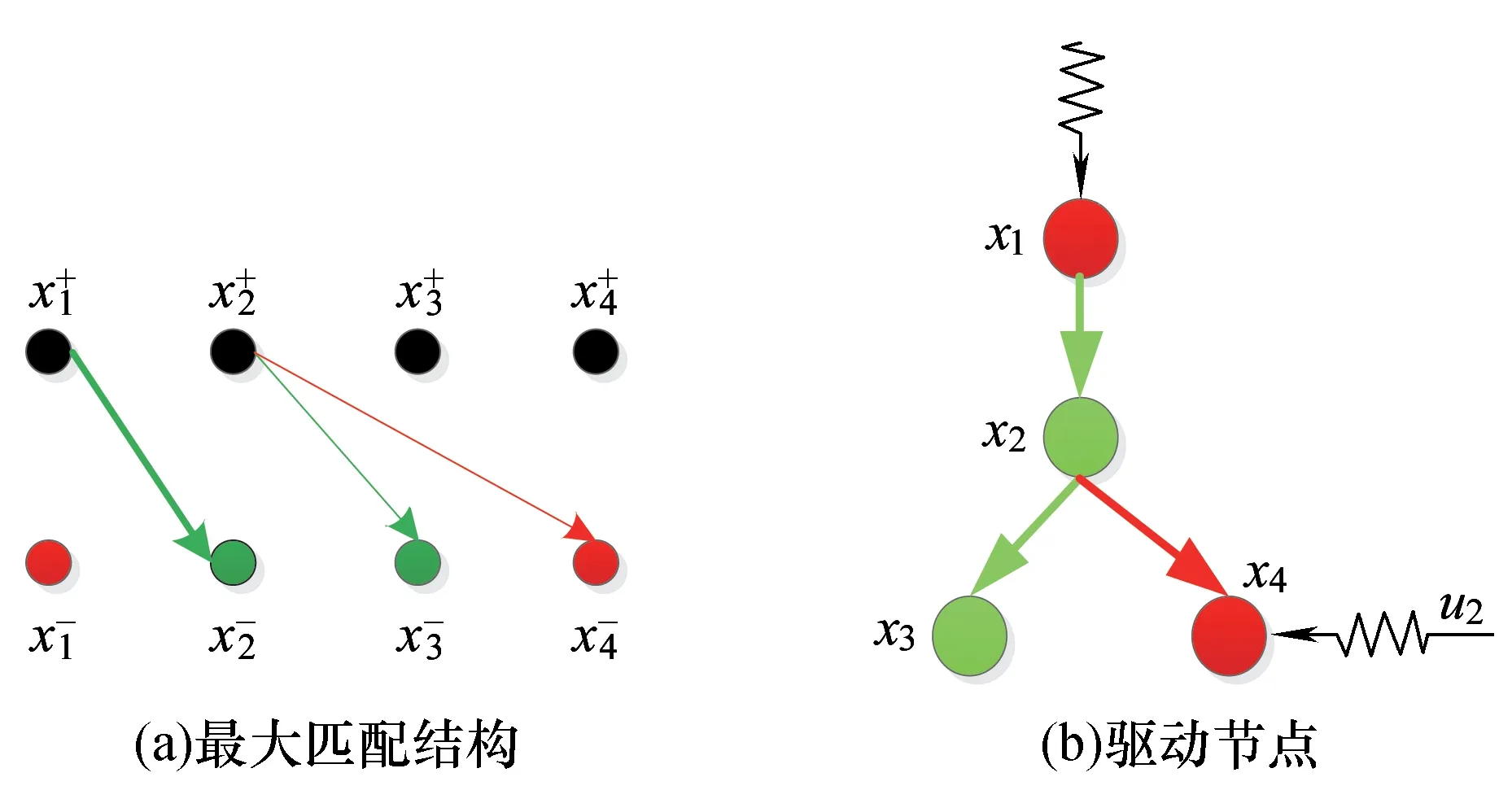
3.2 基于驱动节点匹配的限流车站优化方法

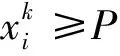

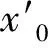

4 案例分析







5 结论
