基于粗糙集理论的列控车载设备故障分析方法

上官伟，张军政，冯 娟，蔡伯根,3，王 剑,李正交

(1.北京交通大学 电子信息工程学院，北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3.北京市电磁兼容与卫星导航工程技术研究中心，北京 100044)

近年来，我国高速铁路发展迅速，取得的成果得到了国内外专业人员的认可，高速铁路已经成为我国走向全球化的响亮名片。同时，作为国家重要的基础设施之一，高速铁路承担着大众生命财产安全的重大责任。因此，列车运行安全问题变得至关重要。科学技术水平的发展，在一定程度上提高了列车运行控制系统的稳定性及可靠性。但也使得车载设备的结构更加复杂，设备故障的发生、演化过程可能是众多内在、外部因素的共同作用，从而导致故障隐患增多且故障耦合程度增大，使得故障不易被发现和确定。因此，列控系统的故障诊断是及时定位故障、保证列车安全运行的关键前提。

故障诊断技术就是定位故障原因的过程，自有工业生产以来就已经存在，并且它是适应工程实际需要而形成和发展起来的一门综合学科。因此，该领域在国内外已经开展了大量研究，并形成了较为深厚的基础。目前可用于工业控制过程的故障诊断技术多种多样，依据理论和方法的不同，故障诊断技术主要包括：基于人工智能的方法、基于数学模型的方法和基于数据驱动的方法[1]。

基于人工智能的故障诊断研究有：文献[2]提出了基于模糊层次分析的柴油机智能故障诊断系统，利用定性和定量相结合的原则结合多Agent技术设计了远程故障诊断系统。文献[3]提出了基于小脑模型神经网络的变压器故障诊断方法，利用小脑模型神经网络具有的自动搜索最大相关性及计算速度快的优势进行仿真计算，仿真结果表明该方法可以有效提高诊断准确率和效率。文献[4]提出了一种基于专家系统的电脑网络连接故障诊断方法，通过实例验证了该专家系统具有较高的诊断效率。文献[5]提出了一种智能诊断方法用于列车转向架轴承的故障诊断，该方法主要分为故障特征提取和故障模式识别两部分，实验结果表明，在提高系统的故障诊断速度和准确性方面该方法具有明显优势。

基于数学模型的故障诊断研究有：文献[6]针对具有工程应用价值的接地网故障诊断问题，基于最小电能消耗原理建立了一种新的数学模型，该模型充分考虑接地网腐蚀严重时本身的非线性特征，仿真结果表明该模型与求解算法是可行的。文献[7]针对飞机喷气发动机，提出了一种基于多模型方法的实时故障诊断与隔离方法，设计了一种模块化和分层体系结构，能够诊断和隔离单个故障以及喷气发动机中的多个并发故障，实验结果表明该方法对于压力和温度传感器的失效以及传感器测量中的大量噪声异常值的诊断也是有效可行的。文献[8]以功率键合图和解析冗余理论为基础，针对法维莱制动系统提出一种解析冗余关系的故障诊断方法，仿真结果表明该方法是有效可行的。文献[9]针对离散控制的连续系统，建立了基于混合动态系统的分散混合诊断器，通过诊断器来协调各个分组件的信息，最终实现有效信息的提取以及故障诊断，能够诊断参数和离散故障。文献[10]提出了一种用于追踪系统模式和诊断混合动力系统的新方法，该方法基于混合自动机HA模型，诊断主要由解释事件完成，对系统的监测则主要由系统的物理参数直接决定，基于案例验证了该方法的有效性。

基于数据驱动的故障诊断方法有：文献[11]为了提高化工装备的故障诊断准确率，提出了一种基于数据驱动的故障检测和隔离方法，该方法通过引入新的特征变量，将简单的过程知识与数据驱动的诊断相结合，通过创建新的特征变量，将基于扩展特征集与原始数据集的故障诊断性能进行了比较，结果表明新属性的加入有效提高了诊断的准确性。文献[12]针对动态系统的故障诊断问题，在简化的非线性频谱模型基础上提出了一种自适应辨识算法，降低了非线性频谱数据求解的计算量，实验表明该算法的故障诊断耗时短，识别率高。文献[13]提出一种增量式数据驱动故障分类方法，以增量学习新的信息来不断完善数据库，自动完成新故障类型的识别，实例证明该方法可明显提高故障诊断的准确率。文献[14]针对电力变压器故障诊断问题的实际特点和支持矢量机方法的条件限制，提出了一种基于改进分类算法和相关矢量机的智能故障诊断方法，该方法改进现有一对一算法的最大投票策略，设计出一种全新的两层最大投票策略，仿真结果表明该方法可以明显增强样本诊断的可信度水平。

随着相关学科的发展以及故障诊断理论研究的深入，故障诊断方法趋于多样化和智能化，且多采用信息融合的方法来实现系统故障的快速高效诊断。但是由于列车运行控制系统的特点，真正适用于列控系统的方法并不多，主要有故障树、专家系统、贝叶斯网络等，但都是基于系统级别，处理基于文本数据类的故障时并不占优势，并存在故障辨识率不高、对不完备知识的处理能力差的缺点。

本文针对以上问题，首先将神经网络NN(Neural Network)应用于含噪声程度不同的列控系统车载设备BTM、TIU故障诊断中，通过对比诊断结果，发现神经网络在数据处理方面存在缺陷，降低了故障识别准确率。为了解决以上问题，进一步提出一种将粗糙集理论RST(Rough Set Theory)与神经网络结合的故障诊断方法RSTNN(Rough Set Theory and Neural Network)，即利用RST的知识约简能力，对通过数据预处理得到的最初决策表进行属性约简，剔除低关联性信息，生成最终决策表，在此基础上利用NN对故障进行分类，通过列控车载设备BTM单元、TIU单元故障诊断案例，验证了该方法在消除噪声、提高故障诊断准确率方面的有效性。

1 基于神经网络算法的车载设备故障诊断

1.1 神经网络分类算法

在众多模式识别分类算法应用中，神经网络模式识别使用较多的网络模型，通常包括两种拓扑结构：多输出型ACON(All Classes One Net)和单输出型OCON(One Class One Net)。

ACON应用最多，典型方法是：网络的每个输入节点对应于样本的一个特征属性；输出层单元采用“c中取1”编码，每个输出节点对应一个类，即输出层单元数等于模式类数；训练样本数据的期望输出为[0，…，1，…，0]，即其所属类的相应输出节点为1，其他节点为0；对于识别阶段，未知样本的类别判定为与输出值最大的节点对应的类别。

经过学习大量的样本，记录调整后的权值，使用此权值数据确定的网络对新的样本进行识别，并计算故障识别准确率和误差范围。

1.2 基于神经网络的故障诊断案例的实现

本文针对CTCS3-300T型车载设备(以下简称300T车载设备)中的TIU单元和BTM单元，利用神经网络分类算法实现故障诊断。

1.2.1 数据预处理

将案例库中的故障代码和故障种类进行编码。TIU单元故障编码过程为：故障代码分别编码为A、B、C、D、E、F、G、H、I、J、K、L、M、N，每一个故障代码对应编码的取值为0或1，1代表样本故障中存在该故障代码，故障种类编码为d。BTM单元故障编码过程为：故障代码分别编码为A、B、C、D、E、F、G、H、I、J、K、L、M、N、O、P、Q、R，取值为0或1，故障种类编码为d，具体编码情况见表1～表4。

表1 TIU单元故障代码编码

表1(续)

注：表1中*的取值为0、1、4、5、6、7、8、9、A、B中的任意值。

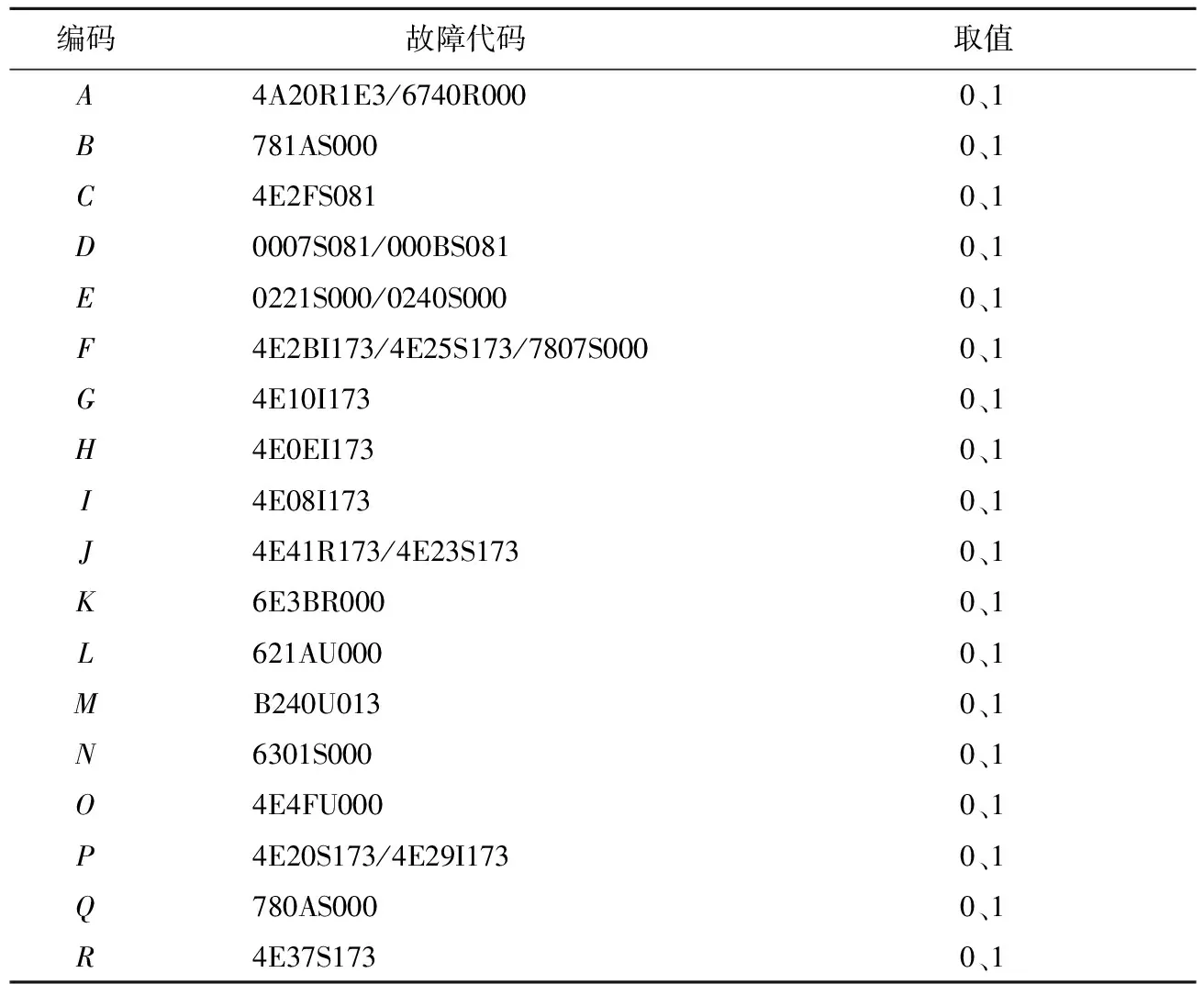
表2 BTM故障代码编码

表3 TIU故障种类编码

表4 BTM故障种类编码

注：表4中的故障种类5很少发生，忽略不计，因此BTM故障种类共5种。

1.2.2 分类规则的确定

故障分类规则由条件属性和决策属性构成的决策表确定。本文将字符编码后的故障代码和故障种类分别作为故障诊断的条件属性和决策属性，生成最初决策表，见表5、表6。

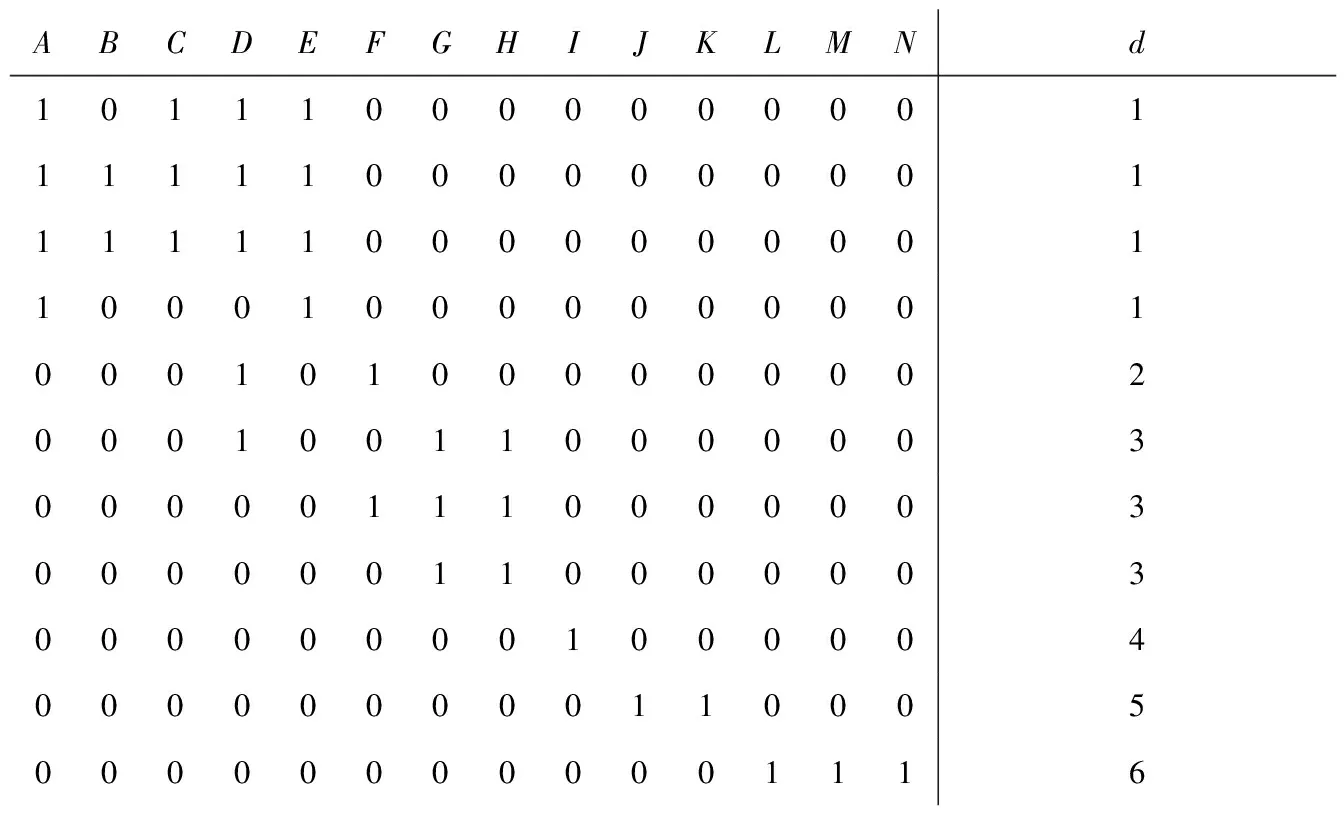
表5 TIU故障诊断决策表

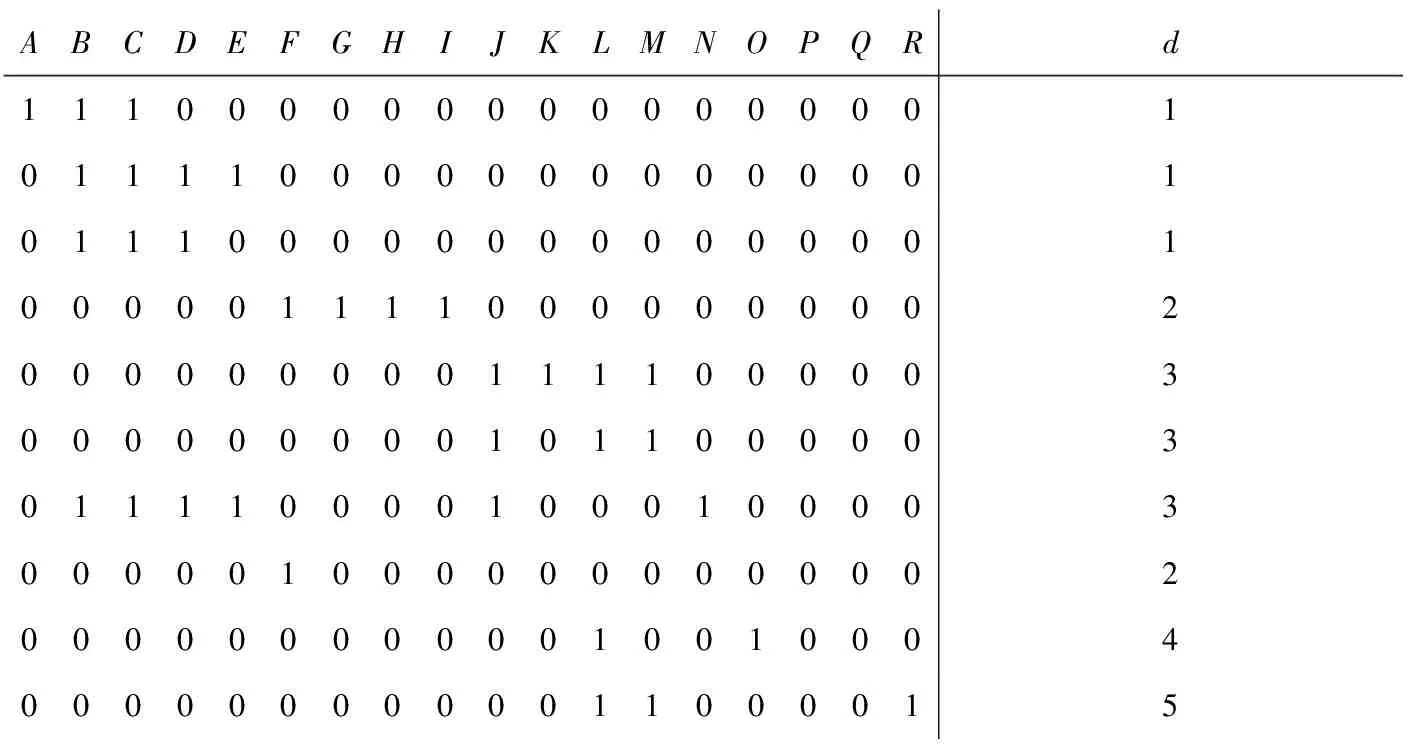
表6 BTM故障诊断决策表

1.2.3 案例仿真与结果分析

基于以上决策表确定的故障诊断规则，采用Matlab软件中的神经网络模式识别工具箱进行仿真，实现列控系统车载设备的故障诊断。

(1)网络构建

整个仿真分为训练和测试两个阶段。针对300T车载设备BTM的故障诊断，选取2015年1月至9月统计的107组BTM类故障数据作为训练样本对网络进行训练。首先，导入网络的输入输出数据。由表2可知，故障代码有18种，故障种类有5种，即网络模型的输入层单元节点数为18，输出层单元节点数为5，模型输出格式经编码后为[1,0,0,0,0]、[0,1,0,0,0]、[0,0,1,0,0]、[0,0,0,1,0]、[0,0,0,0,1]。设置输入单元节点数18个，隐含层单元数20个，输出单元节点数5个，在模式识别工具箱中选取90%、5%、5%的故障数据集分别对应训练、验证、测试部分，其中验证、测试部分是对训练部分的初步检验。然后，对样本进行多次训练。

对基于以上训练得到的网络进行相应测试。选取2015年10月至12月的72组BTM类故障作为测试样本。

对于TIU单元的故障诊断，采用2015年1月至6月统计的100组TIU类故障数据中的60组数据作为训练样本，40组数据作为测试样本，特征数为14，输出类别为5个。同样基于神经网络模式识别工具箱进行仿真。

(2)仿真结果与分析

基于上述样本数据，对网络进行100次训练与相应的测试，仿真结果如图1、图2所示。

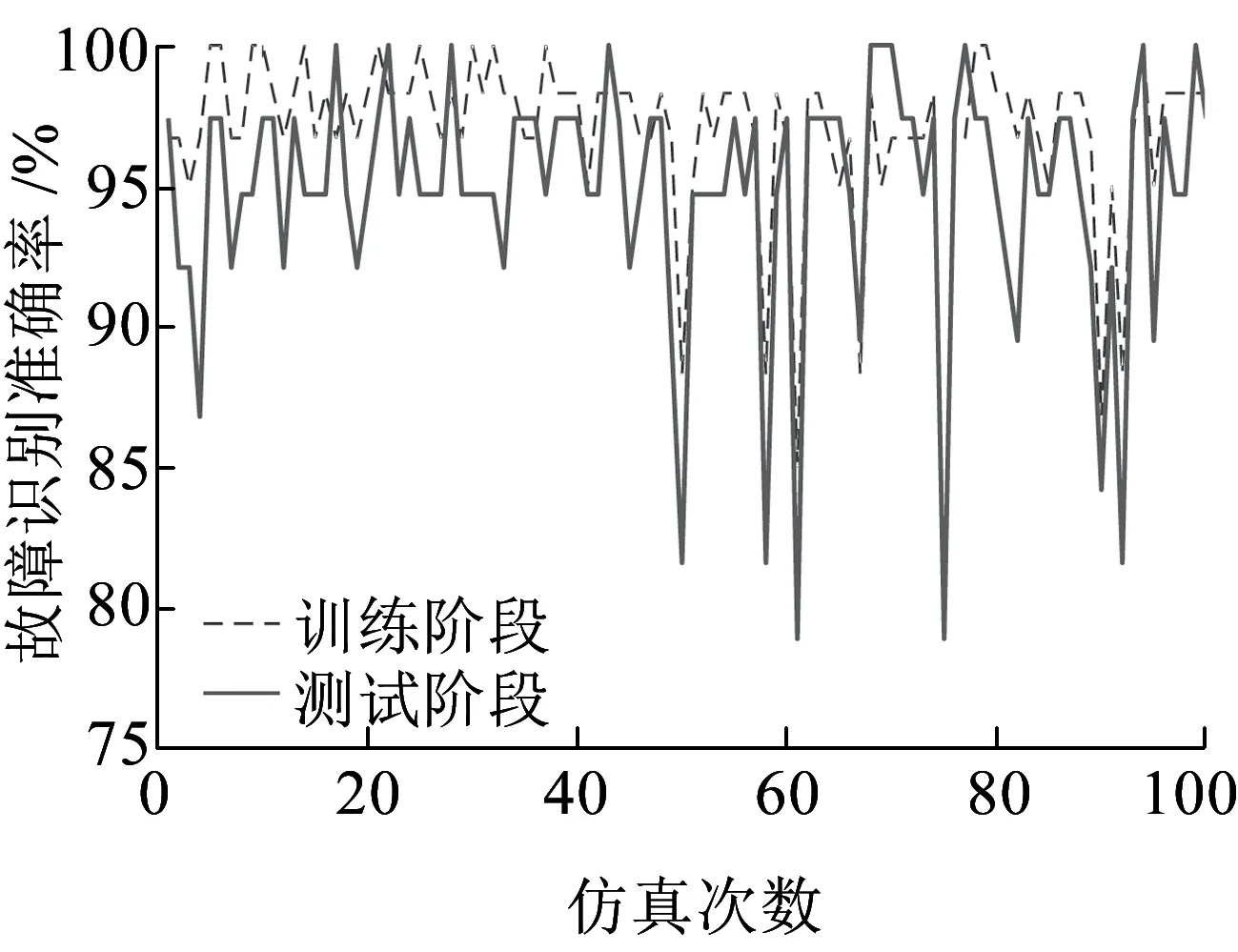
图1 TIU故障分类结果

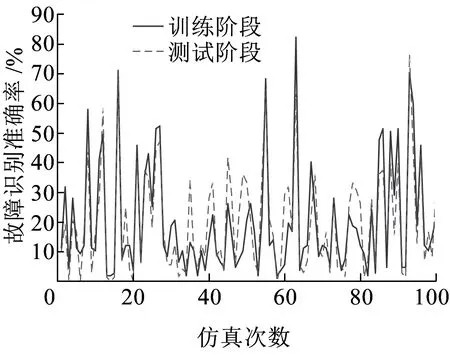
图2 BTM故障分类结果

由图1和图2可知，基于相同的规则进行仿真，神经网络对TIU故障分类效果明显优于BTM类。由于BTM类故障原始数据含噪声较大，因此故障识别准确率基本上低于50%，其平均值是：训练部分为19.89%，测试部分为36.51%。而TIU类故障的原始数据含噪声比较小，故障识别准确率基本上高于90%，训练部分和测试部分的识别准确率平均值分别为96.93%和94.84%。

由以上两种300T车载设备的故障识别率仿真结果可知，神经网络无法从低关联度的初始数据中完成重要信息的存取、消除高噪声，从而使故障辨识准确率低效不可用，仿真验证结果严重震荡且发散。因此，神经网络算法对高冗余数据进行分类时存在严重不足，为克服以上缺点，提高故障诊断能力，本文引入了粗糙集理论来改进神经网络对高噪声故障数据的分类识别能力，实现对列控系统车载设备的故障诊断。

2 基于改进型神经网络的列控车载设备故障诊断

2.1 粗糙集理论

粗糙集理论的出发点是在维持识别特性不变的情况下，通过将数据集进行预处理和属性约简，清洗其中关联度低或无用的属性，在约简的属性表中发现分类规则。作为数据挖掘常用的算法之一，粗糙集理论的优势逐步凸显，其在工程领域方面的应用也变得越来越多，但在列控系统方面的应用较少，值得进一步研究。

属性重要度的计算方法有多种，本文采用基于区分矩阵计算属性重要度的方法。记录生成的区分矩阵中每个属性出现的频率，以此作为评估属性重要度的参考指标。该方法不是简单计数，而是以加权方式求得，权重分配的大小以属性所在区分矩阵的长度而定，即当不同属性的频率相同时，包含在长度越短的区分矩阵的元素属性越重要[15]。

设知识库为K=(U,R)，其中，U为研究对象构成的集合，称为域；R为U上的一个等价关系。ind(K)定义为K中所有等价关系的族，记作

ind(K)={ind(P)|Ø≠P⊆R}

( 1 )

令P为一族等价关系，如果

ind(P)=ind(R-{P})

( 2 )

则称P为R中不必要的；否则称P为R中必要的。

设知识表达系统为S=(U,A,V,f)，|U|=n，S的区分矩阵是n×n的对称矩阵。A表示所有属性构成的集合，V为属性的取值，f为信息函数。矩阵中的每一项元素mij为

( 3 )

式中：i,j=1,2,…,n。矩阵包含的内容是属性集，表示两个对象在该属性集上的值不同。

设Q⊆P，如果Q是独立的，且ind(Q)=ind(P)，则称Q为P的约简；P的所有约简的交集称为P的核，记作core(P)，核也可能为Ø。信息系统的核等于该信息系统的区分矩阵中所有单个属性元素组成的集合。

对于一个区分矩阵Mn×n=(cij)n×n，属性α∈C的重要性计算公式为

( 4 )

其中

( 5 )

式中：i,j=1,2,…,n；|cij|表示区分矩阵中元素cij的长度(包含条件属性的个数)。

2.2 算法描述

通过粗糙集理论对神经网络技术进行改进，形成300T车载设备故障诊断步骤，即利用粗糙集理论在数据挖掘方面的属性约简和模糊不完整信息处理的特性，对应答器传输单元故障数据、列车接口单元故障数据进行清洗，去除噪声，实现属性约简与优选，最后利用NN实现对300T车载设备BTM和TIU的故障识别。基于粗糙集理论的神经网络算法RSTNN的故障诊断步骤如图3所示。

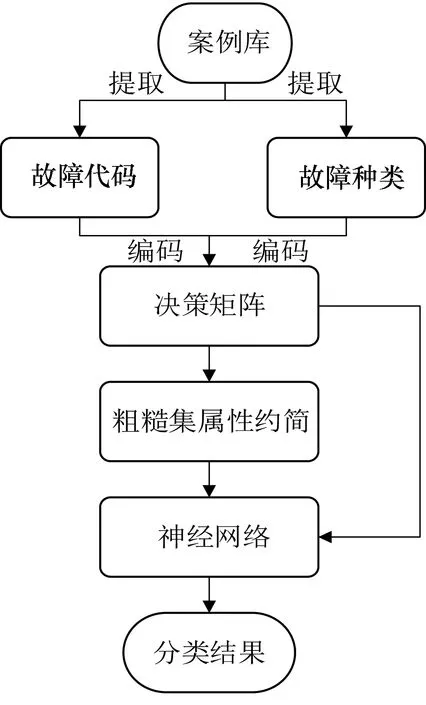
图3 故障诊断步骤

2.3 基于改进型神经网络算法的车载设备故障诊断的实现

2.3.1 基于粗糙集理论的属性约简

粗糙集属性约简的一般步骤如图4所示。由RST可知，结合300T车载设备故障案例特点，属性约简的具体步骤为：对案例库中的故障代码和故障种类分别编码，生成最初决策表；基于RST知识进行推理，求出必要属性和区分矩阵，如表7和图5所示；根据核属性及属性重要度的定义，由区分矩阵求出核属性以及重要属性，从而求出初步决策表，其中属性重要度见表8，初步决策属性见表9；基于集合间的包含关系对初步决策表进行改进，得出最终的属性约简决策表。

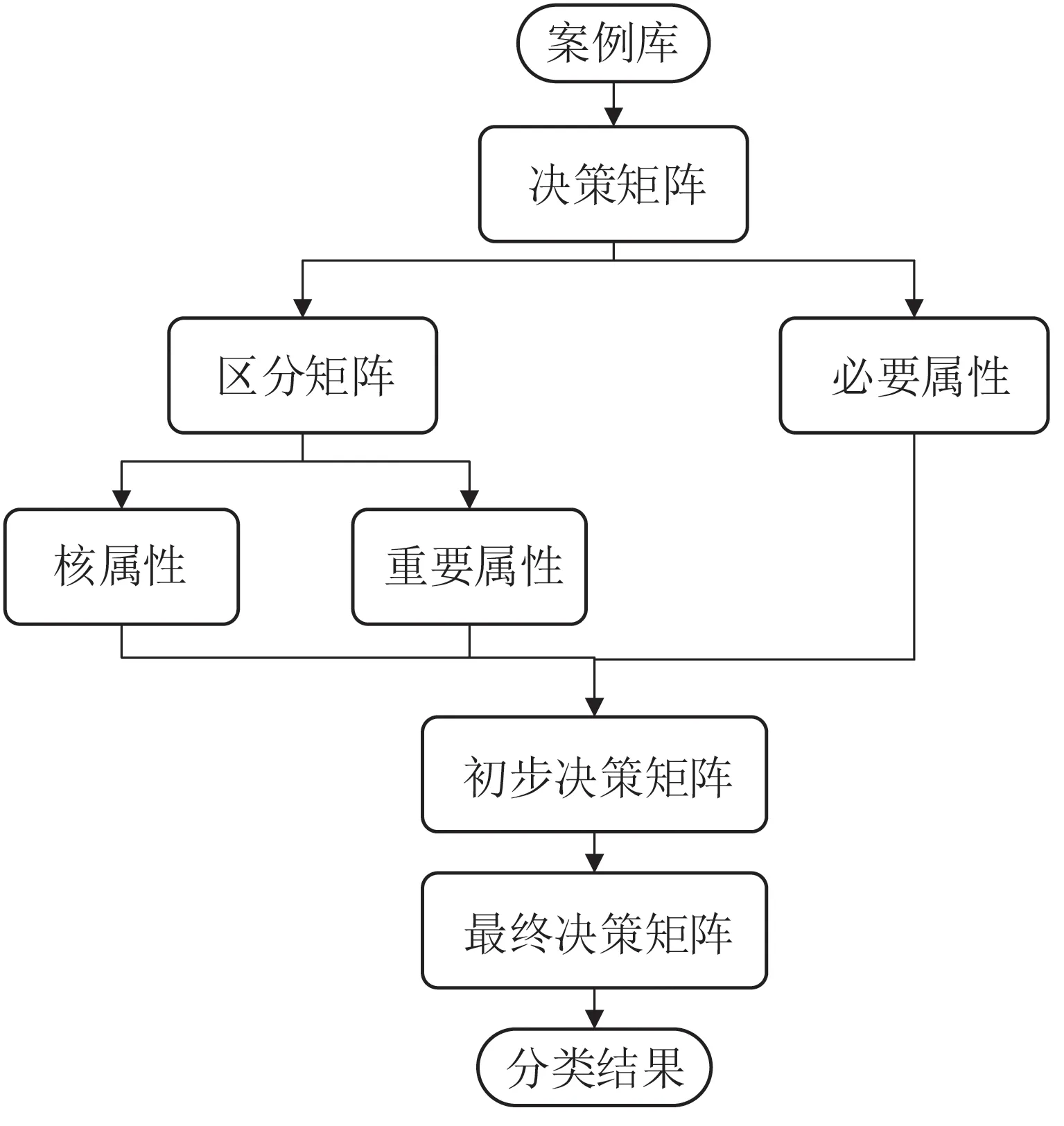
图4 粗糙集属性约简步骤

设该知识系统为S={U,R}。其中，U为{A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R}，R为d。详细操作步骤为：剔除最初决策表中的重复事件3和10；确定出必要属性、核属性、重要属性以及决策矩阵。

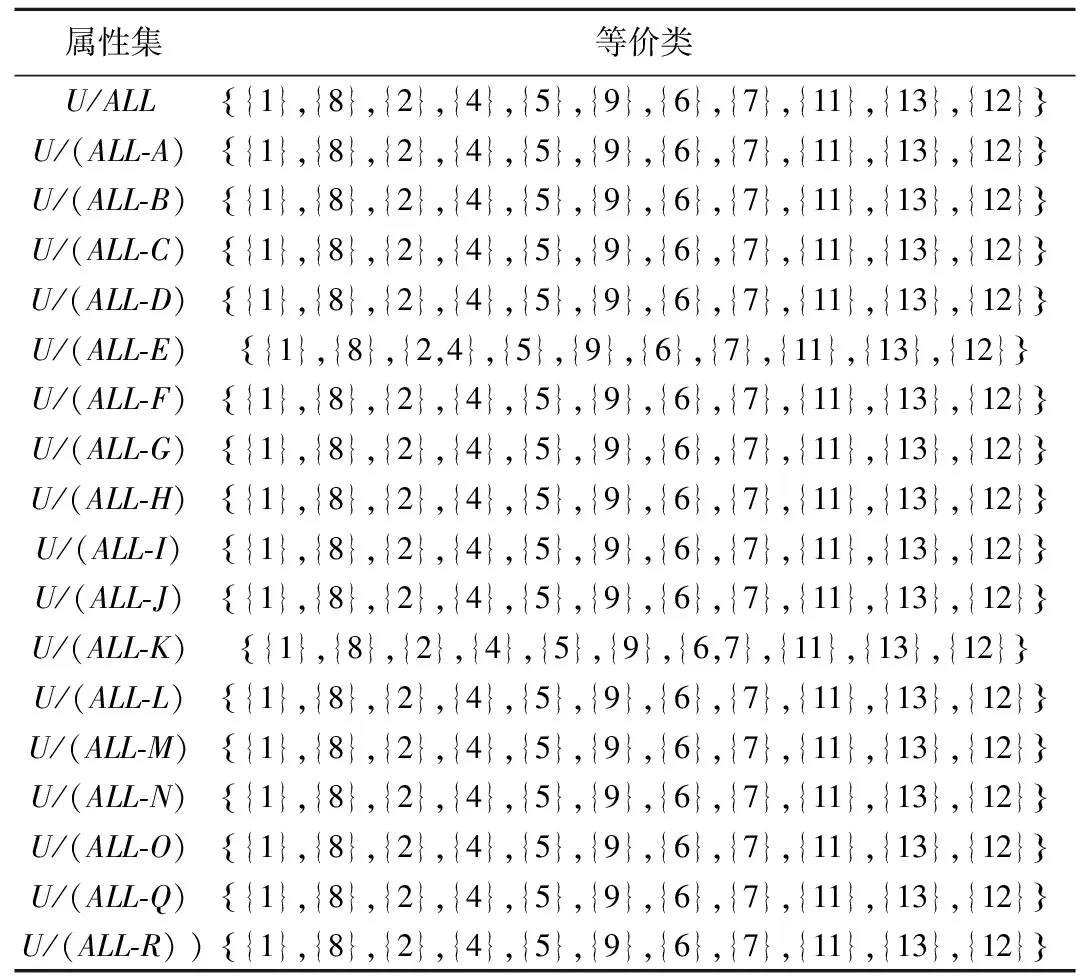
表7 必要属性判断

注：表中U/ALL为全部属性的结果集，U/(ALL-A)为剔除属性A之后的结果集。

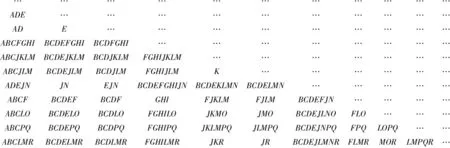
图5 区分矩阵

表8属性重要度

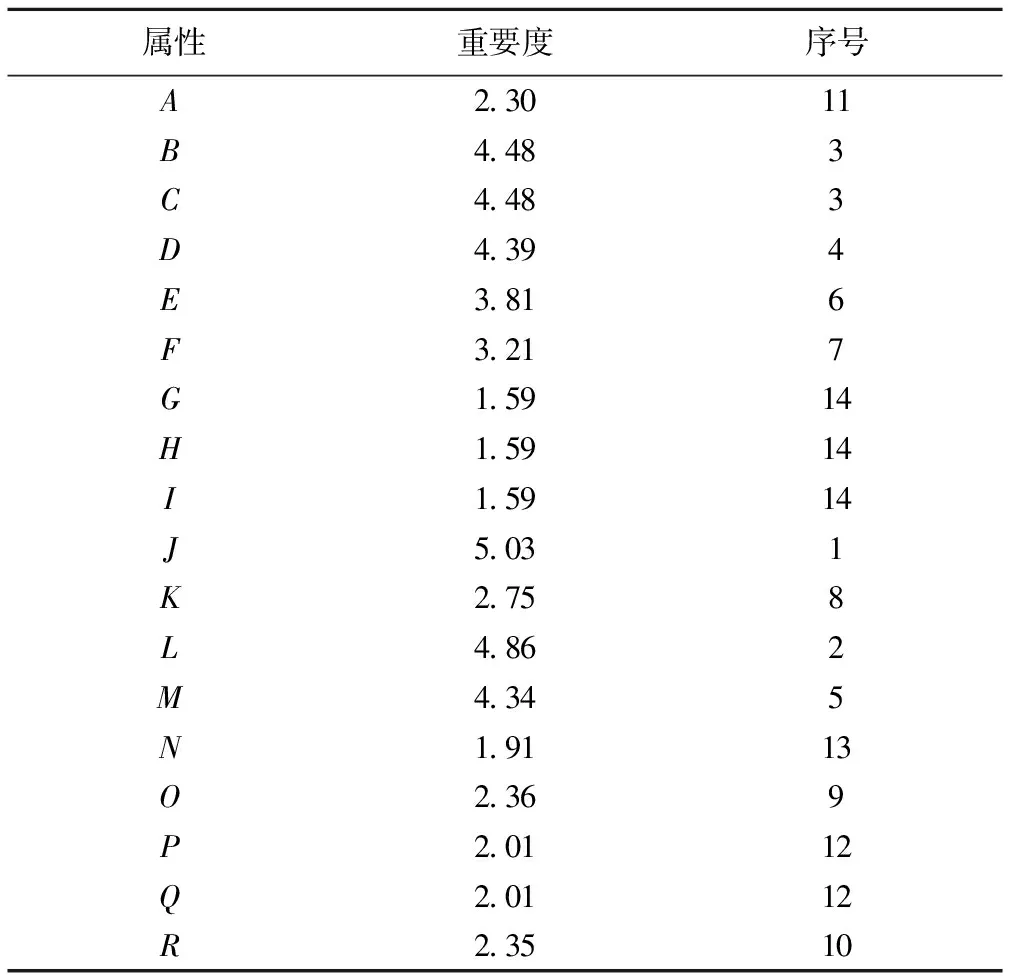
属性重要度序号A2 3011B4 483C4 483D4 394E3 816F3 217G1 5914H1 5914I1 5914J5 031K2 758L4 862M4 345N1 9113O2 369P2 0112Q2 0112R2 3510

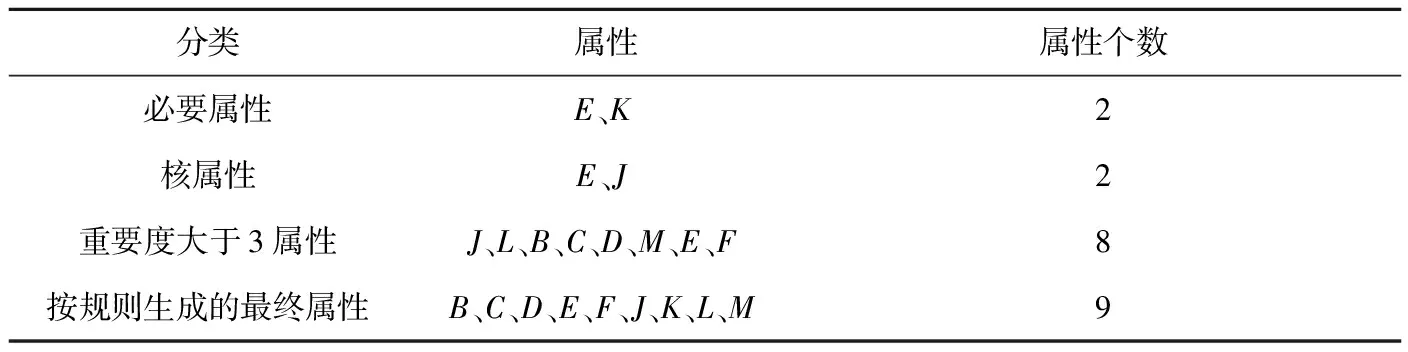
表9 初步决策属性

基于集合间的包含关系[16]，对初步决策表进行属性约简。

对于种类1，事件1、2、4对应的属性集为{B,C}、{B,C,D,E}、{B,C,D}，考虑集合间的包容关系，得出重要属性为{B,C}；种类2的重要属性为{F}；种类3的重要属性为{J}；种类4的重要属性为{L}；种类6的重要属性为{L,M}。

种类4和种类6之间的特征属性也存在包容关系，因此加入属性O提高二者的可识别度。

经过以上改进，得出最终决策表见表10。

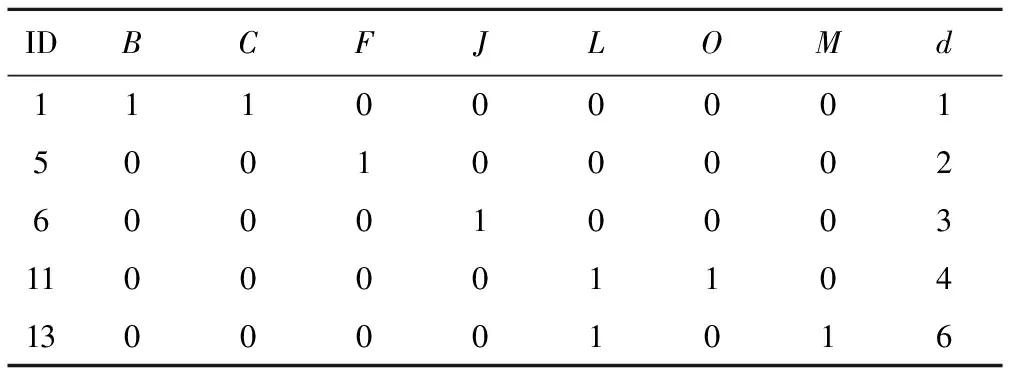
表10 BTM故障属性约简后的最终决策表

基于同样的方法对TIU故障数据进行处理，最终得出TIU故障的决策表见表11。

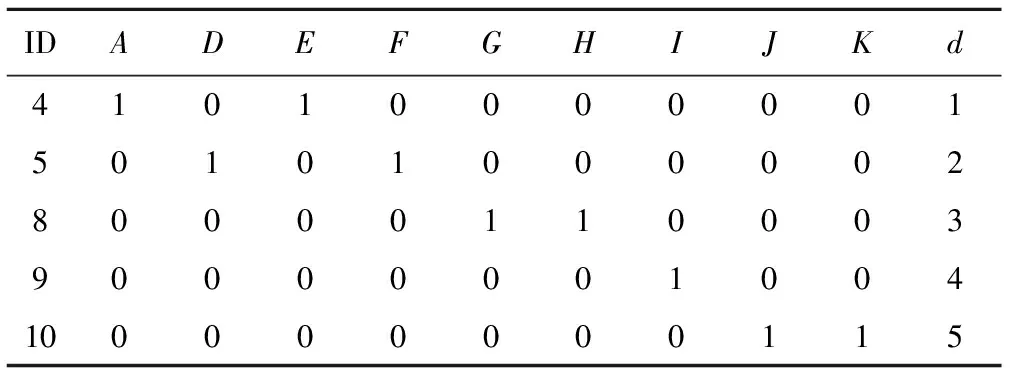
表11 TIU故障属性约简后的最终决策表

2.3.2 基于RST的NN车载设备故障诊断仿真

(1)网络构建

整个仿真分为训练和测试两个阶段。针对300T车载设备BTM的故障诊断，选取2015年1月至9月的107组统计故障数据完成网络训练。首先，导入网络的输入输出训练数据样本。经过RST对最初决策表约处理的属性个数为7，即输入节点数为7；输出层节点数即故障种类为5，对应的编码分别为[1,0,0,0,0]、[0,1,0,0,0]、[0,0,1,0,0]、[0,0,0,1,0]、[0,0,0,0,1]。设定输入单元为7个节点，隐含层的单元数和输出节点数保持不变。然后，对故障样本数据进行多次训练。

选取2015年10月至12月的72组故障数据利用以上训练得到的神经网络进行仿真测试。

针对300T车载设备TIU的故障诊断，选取2015年1月至6月统计的100组数据进行仿真，采用其中的60组数据作为训练样本，40组数据作为测试样本。

(2)仿真结果与分析

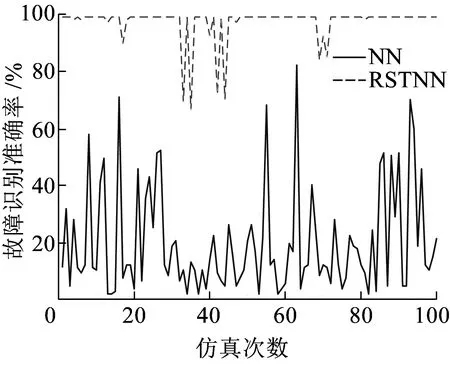
(a)BTM训练阶段仿真结果对比

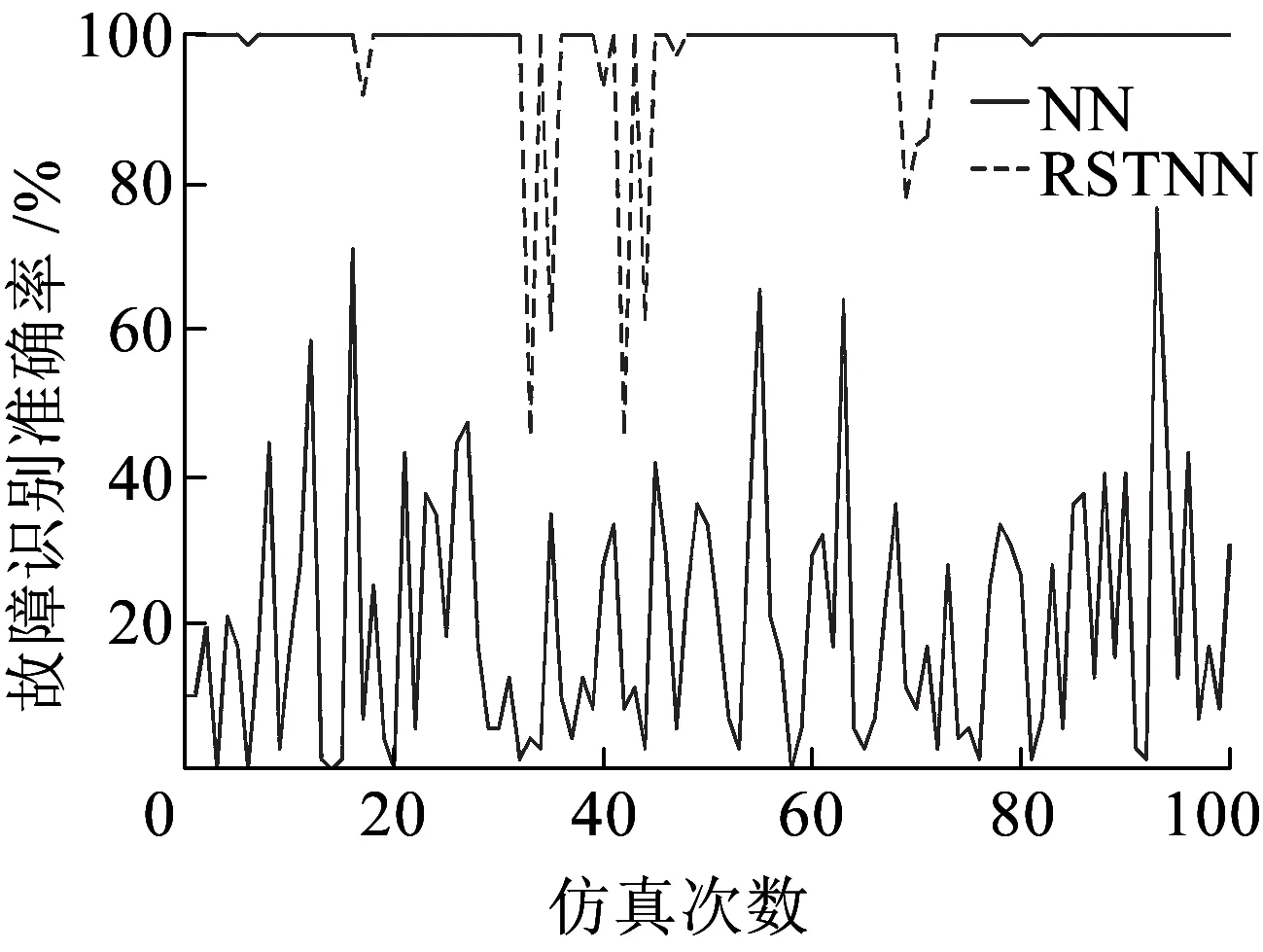
(b)BTM测试阶段仿真结果对比

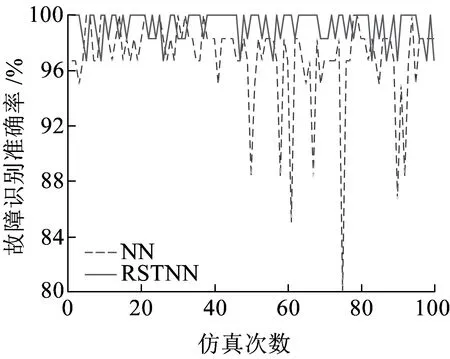
(c)TIU训练阶段仿真结果对比

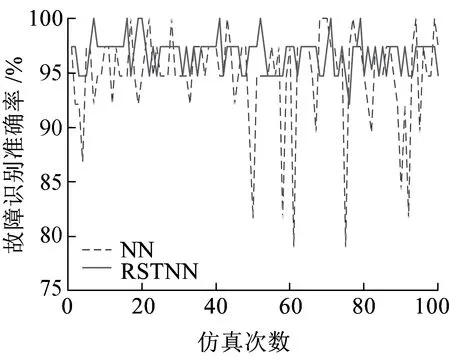
(d)TIU测试阶段仿真结果对比图5 基于RSTNN算法的BTM和TIU仿真结果

基于RSTNN算法的BTM和TIU仿真结果如图5所示。由图5(a)和图5(b)可知，通过粗糙集理论对神经网络输入层特征数据的属性进行约简后，300T车载设备BTM单元的故障识别准确率的平均值上升为训练部分93.32%、测试部分97.41%，比基于神经网络的仿真结果提高了3～5倍，表明基于粗糙集的神经网络算法在去除数据中的低关联度信息和不完整数据方面有明显的作用。由图5(c)和图5(d)可知，对于识别准确率比较高的TIU单元故障，经过粗糙集理论对原始数据进行处理后，其故障识别准确率在训练部分和测试部分较之前分别提高了2.28%和1.88%。由此可知，基于RST的NN模型既能对不精确性和低关联度的数据进行处理，还能保留原始数据的关键属性信息。综合图5可知，利用RST对NN模型改进后，仿真结果波动范围减小，并随着仿真次数的增加，网络快速趋于收敛。如图5(a)所示，训练至70次左右，网络基本处于收敛状况。

3 结束语

本文针对神经网络方法在数据高噪声背景下实现300T车载设备故障诊断过程中辨识率较低的问题，提出一种改进的神经网络模型故障诊断方法，即利用RST对属性的约简能力，对原始决策规则进行属性约简，去除噪声，从而得出新的故障诊断规则，然后采用NN算法对故障分类，并将其应用到300T车载设备的BTM单元和TIU单元，从而验证了该方法在列控系统车载设备故障诊断方面的可行性。

粗糙集理论和神经网络算法的结合可以很好地弥补神经网络算法作为分类器对数据质量依赖程度大的缺陷，从而实现两种算法的优势互补，保证诊断精度，对实现列控系统车载设备的故障诊断具有一定的理论意义和实用价值。

参考文献：

[1]LEO M S, RUSSELL E L, BRAATZ R D. Fault Detection and Diagnosis in Industrial Systems[J]. Measurement Science & Technology, 2001, 12(10):453-454.

[2]蒋苹, 何清华, 王奕. 基于模糊层次分析的柴油机智能故障诊断[J]. 中国工程机械学报, 2009, 7(1):86-91.

JIANG Ping, HE Qinghua, WANG Yi. Fuzzy AHP-based Intelligent Fault Diagnosis for Diesel Engine[J]. Chinese Journal of Construction Machinery, 2009，7(1)： 86-91.

[3]PAI N S, LAI Y C. Fault Diagnosis of Electric Power System Transformer on CMAC Neural Network Approach[C]//International Conference on Fuzzy Theory and Its Applications.New York:IEEE, 2012:158-162.

[4]KHALID R, JASSIM R. Expert Diagnosis Systems for Network Connection Problems[C]//International Conference on Artificial Intelligence, Modelling and Simulation. New York:IEEE, 2014:15-18.

[5]刘建强, 赵治博, 任刚,等. 基于小波包分解和集合经验模态分解的列车转向架轴承智能故障诊断方法[J]. 铁道学报, 2015,37(7):40-45.

LIU Jianqiang, ZHAO Zhibo, REN Gang, et al. An Intelligent Fault Diagnosis Method for Bogie Bearings of Train Based on Wavelet Packet Decomposition and EEMD[J]. Journal of the China Railway Society, 2015, 37(7):40-45.

[6]王福胜, 郭洁, 王川龙. 接地网故障诊断的数学模型[J]. 工程数学学报, 2011, 28(5):623-628.

WANG Fusheng, GUO Jie, WANG Chuanlong. Mathematical Model for the Fault Diagnosis of Grounding Grid[J]. Chinese Journal of Engineering Mathematics, 2011, 28(5):623-628.

[7]MESKIN N, NADERI E, KHORASANI K. A Multiple Model-Based Approach for Fault Diagnosis of Jet Engines[J]. IEEE Transactions on Control Systems Technology, 2012, 21(1):254-262.

[8]黄志武, 刘建刚, 刘伟荣,等. 基于解析冗余关系的法维莱制动机系统故障诊断技术[J]. 铁道学报, 2013, 35(3):29-35.

HUANG Zhiwu, LIU Jiangang, LIU Weirong, et al. Fault Diagnosis of Faiveley Braking System Based on Analytical Redundancy Relations[J]. Journal of the China Railway Society, 2013, 35(3):29-35.

[9]LOUAJRI H, SAYED-MOUCHAWEH M. Decentralized Structure for Fault Diagnosis of a Class of Hybrid Dynamic Systems[C]// Control and Automation. New York:IEEE, 2014:121-126.

[10]VENTO J, TRAVE-MASSUYES L, PUIG V, et al. An Incre mental Hybrid System Diagnoser Automaton Enhanced by Discernibility Properties[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2015, 45(5):788-804.

[11]YAMASHITA Y. Knowledge-based Attributes Generation for Data-driven Fault Diagnosis in Process Systems[J]. Computer Aided Chemical Engineering, 2012, 31(4):310-314.

[12]张家良, 曹建福, 高峰,等. 基于非线性频谱数据驱动的动态系统故障诊断方法[J]. 控制与决策, 2014,29(1):168-171.

ZHANG Jialiang, CAO Jianfu, GAO Feng, et al. Fault Diagnosis Approach of Dynamic System Based on Data Driven of Nonlinear Spectrum[J]. Control & Decision, 2014, 29(1):168-171.

[13]SANKAVARAM C, KODALI A, PATTIPATI K R, et al. Incremental Classifiers for Data-driven Fault Diagnosis Applied to Automotive Systems[J]. IEEE Access, 2015(3):407-419.

[14]吴坤, 康建设, 池阔. 基于改进多分类算法和相关矢量机的电力变压器故障诊断方法[J]. 高电压技术, 2016, 42(9):3011-3017.

WU Kun, KANG Jianshe, CHI Kuo. Fault Diagnosis Method of Power Transformers Using Improved Multi-class Classification Algo-rithm and Relevance Vector Machine[J].Journal of High Voltage Technology, 2016, 42(9):3011-3017.

[15]陈楠. 基于粗集理论的增量式属性约简研究[D]. 长春：长春理工大学, 2005.

[16]王加阳, 高灿. 改进的基于差别矩阵的属性约简算法[J]. 计算机工程, 2009, 35(3):66-67.

WANG Jiayang, GAO Can. Improved Algorithm for Attribute Reduction Based on Discernihility Matrix[J]. Computer Engineering, 2009,35(3):66-67.