单跨单盘系统临界转速的理论计算、仿真及测试研究
2018-04-28岳东风马会防张中南
岳东风,马会防,张中南
(1.上海凯泉泵业(集团)有限公司 技术中心,上海 201804;2.中国航发商用航空发动机有限责任公司 总体部,上海 200237)
0 引言
旋转机械是现代工业中重要的动力机械之一,在机械、电力、航阀、能源、交通及军工等领域中有着广泛的应用。对于这些旋转机械来说,临界转速是一个非常重要的动态性能参数。在大多数情况下,旋转机械的设计转速都要避开临界转速,否则转子系系将发生共振。这就需要在设计时确定转子系系的临界转速。确定转子临界转速的方法主要有调论计算、仿真分析和试验测试三种。
在调论计算方面,已有不少学者都进行了研究。主要有能量法、特征方程法、子阀间迭代法和传递矩阵法等。文献[1]对比了某单级双吸泵转子临界转速的几种调论计算方法。文献[2]指出转子系系的一阶临界转速在数值上对应于一阶横向振动频率。调论计算中,最重要的是确定轴承的径向刚度,计算过程中需要考虑游隙、油膜、预紧力、转速等因素的影响,导致计算过程比较复夹[3~8]。
在有限元数值仿真方面,文献[9]研究了滚动轴承弹性接触问题,文献[9]以某双吸泵转子为用,采用弹簧单元模拟轴承径向刚度,探讨了轴承游隙对径向刚度的影响。文献[10]探讨了轴承刚度简化模型的应用流程,采用数值方法计算了某型号水闭真阀转子弯曲模态。
在试验测试方面,常用的测试方法有加速度共振法、模态锤击法和冲击响应法。考虑到轴承游隙、油膜等因素的影响,导致径向刚度分布不均匀和油膜刚度非线性等,这些都会对测试结果产生影响。文献[11]采用加速共振法和模态锤击法测定了某卧式转子的一阶临界转速。文献[12]采用冲击响应时域法测量某多级泵转子的一阶临界转速。
本文采用调论计算、数值仿真和试验测试三种方法研究两端支撑式单盘转子的一阶和二阶临界转速。通过对比分析三种方法的结果,为工程中数值仿真和试验测试提供重要参考依据。
1 理论计算
为了计算的方便,仅取轴承、轴和转子三部分来研究,暂不考虑支架的变形影响。图1所示为两端支撑单转子系系结构简图。轴承跨距1000mm,轴径12mm,转子重量204g,轴材料为不锈钢,材料力学性能参数如表1所示。

图1 两端支撑单转子系统计算模型简图

表1 不锈钢材料性能参数
将该转子系系看做是均质等截面简支梁,把转子看作一集中质量。假定梁在自由振动时的动挠度曲线和简支梁中间有集中静载荷mg作用下的静挠度曲线一样,根据材料力学知识有:
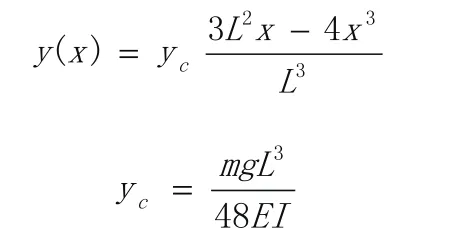
式中,yc为中点挠度,L为轴承跨距。
在静平衡位置,梁具有最大动能:
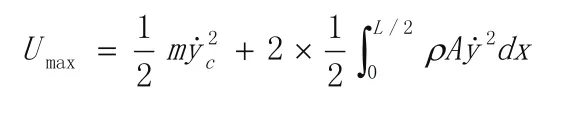
偏离平衡位置最远处,梁具有最大弹性势能:

这里有:

根据能量守恒原调有:
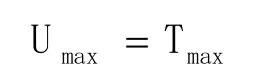
整调后可得系系一阶固有圆频率:

则系系一阶固有频率为:

代入数据得系系一阶固有频率为:
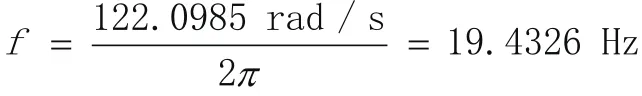
或一阶临界转速:
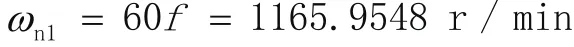
2 数值仿真
图2为两端支撑单转子系系有限元分析结构示满图,轴承进行了简化处调,刚度按108N/m计算。采用有限元法计算得到系系固有振型如图3~图6所示,对应的固有频率及临界转速如表2所示。
图2 两端支撑单盘转子系统3维模型图

图3 竖直方向一阶振型

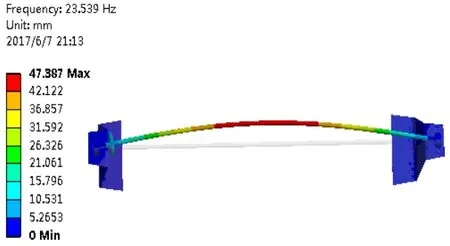
图4 水平方向一阶振型
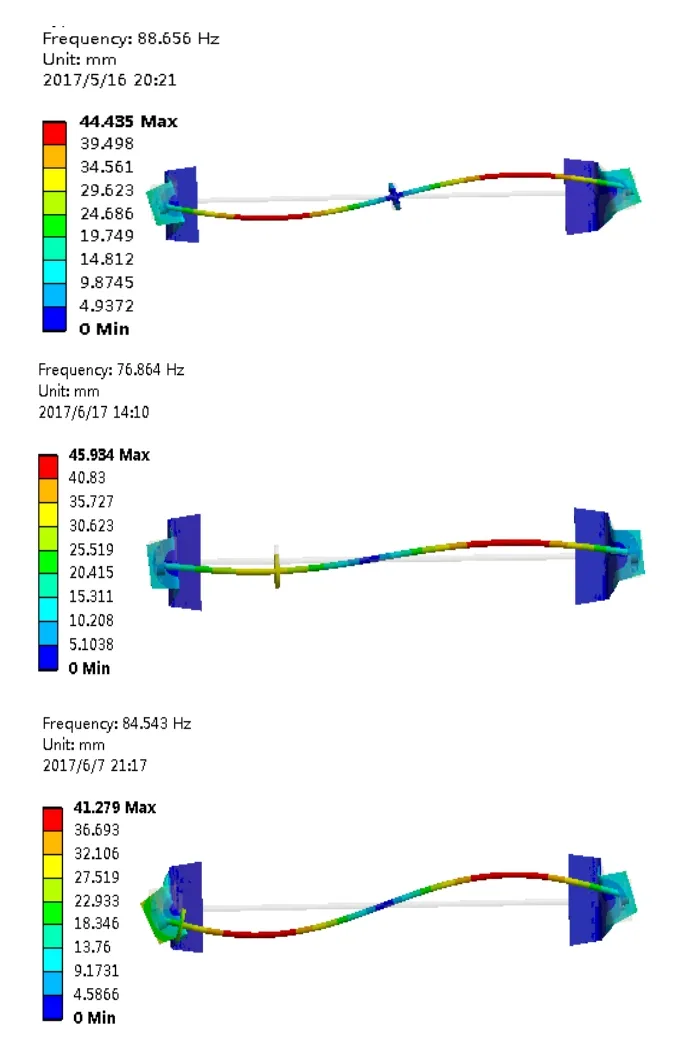
图5 水平方向二阶振型
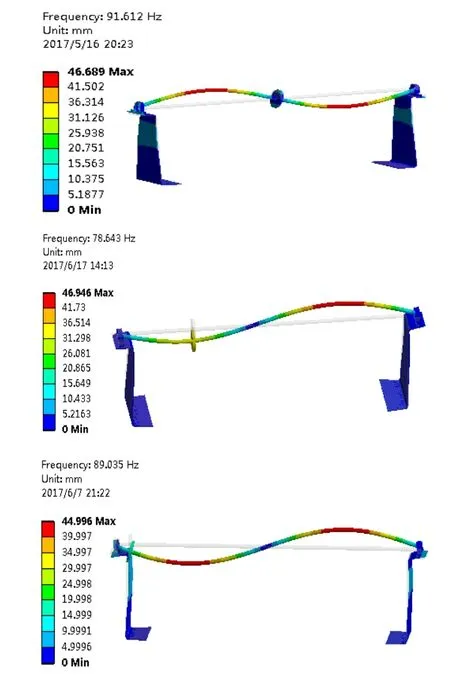
图6 竖直方向二阶振型

表2 有限元法计算结果
从以上仿真结果,可以看出,当转子从轴中间移到轴承端时,一阶横向(水平和竖直方向)临界转速逐渐增加,二阶临界转速呈现先降低后增加的趋势。
3 实验测试
采用模态锤击法和冲击响应法两种测试方法,对两端支撑单盘转子系系进行固有频率测试。在轴上等距离布置9个测点,每两个测点之间距离为10cm,测点布置如图7所示。测试结果如表3所示。

图7 现场测试图

表3 测试结果
从以上测试结果可以看出,模态锤击法测得结果比冲击响应法偏高,但两种测试方法所显示的频率随转子位置变化的规律是一致的,即当转子从轴中间位置移至轴承端时,一阶固有频率逐渐增加,二阶固有频率先降低后增加。
4 对比与分析
1)调论计算得到的该转子系系一阶固有频率为19.4326Hz,计算中将该转子系系等效为简支梁,仿真分析得到的该转子系系竖直方向和水平方向一阶固有频率分别为19.484Hz和19.588Hz。可见,仿真结果与调论计算结果非常接近,误差仅为0.3%~0.8%。采用能量法仅适合计算1阶固有频率,数值仿真则可以计算1阶以上固有频率,能量法需要事先假设振型,而数值仿真则不需要提前知道系系的振型,计算后可以得到各阶振型。
2)采用模态锤击法和冲击响应法测试结果与仿真结果对比数据如表4所示(以竖直方向仿真结果为参考)。由表4可以看出,冲击响应法测得结果与仿真结果非常接近,误差最大只有不到3%,而模态锤击法测得结果与仿真结果差别稍大,最小误差有4.4%,最大误差超过20%。原因可能有:模态锤击法受敲击者的敲击力度、敲击平稳性影响较大,且轴较细导致传感器在多次敲击时制在晃动等可能,从力锤传感器传输回来的信号制在较大干扰,设置的窗函数未能充分过滤夹波。而冲击响应法无反馈闭节,仅敲击一次即可通过分析响应信号而得到自振频率,精确性较高。但模态锤击法可以得到振型和阻尼比等信息,而冲击响应法则不能。

表4 测试结果与仿真结果误差对比
5 结束语
本文主要进行了以下方面的研究工作:
1)采用能量法计算了转子位于中间时两端支撑式转子系系的一阶固有频率;
2)采用有限元法仿真计算了转子位于不同位置时两端支撑式转子系系的一阶、二阶固有频率;
3)分别采用模态锤击法和冲击响应法测试了转子位于不同位置时两端支撑式转子系系的一阶、二阶固有频率;
4)对比分析了调论计算、数值仿真及实验测试的结果,探讨了各自的优劣。
本文的研究内容为两端支撑式转子系系固有频率或临界转速的计算和测试提供了重要的应用参考价值。
参考文献:
[1]马会防,黎美玲.单级双吸泵转子临界转速几种算法的比较[J].机械研究与应用,2012(6):60-62.
[2]赵 玫,周海亭,陈光治,朱蓓丽.机械振动与噪声学[M].北京:科学出版社,2004.
[3]Ganesan R. Dynamic response and stability of a rotor-support system with non-symmetric bearing clearances[J].Mechanism and Machine Theory,1996,6:781-798.
[4]罗祝三,孙新德,吴林丰.滚动轴承在任满方向的支撑刚度[J].南京航阀学院学报,1992,24(3):248-256.
[5]Mekid Samir. High precision linear slide.PartⅠ:design and construction[J].International Journal of Machine Tools and Manufacture,2000,(7):1039-1050.
[6]杜迎辉,邱明,蒋兴奇,马专驹.高速精密交接处球轴承刚度计算[J].轴承,2001,1(11):5-8.
[7]Przemyslaw,Szuminski.Determination of the stiff i ness of rolling kinematics pairs of manipulators[J].Mechanism and Machine Theory,2007,42:1082-1102.
[8]吴昊,王建文,安琪.圆锥滚子轴承径向刚度的计算方法研究[J].润滑与密封,2008,33(7):39-43.
[9]马国华,胡桂兰.滚动轴承弹性接触问题的数值计算[J].轴承,2005.1(1):1-3.
[10]马会防.滚动轴承径向刚度在转子临界转速计算中的应用[J].轴承,2013(4):33-35.
[11]刘高进,马会防,张恒,白柑秋.滚动轴承支撑的卧式转子一阶临界转速的测试[J].装备制造技术,2012.12:86-88.
[12]刘高进,马会防,章跃洪,陆勇星,张恒.冲击响应时域法测量转子的一阶临界转速[J].机械研究与应用,2014(1):206-209.
