基于离散曲率的自由曲面自适应测量技术
2018-04-28闫如忠张文辉
闫如忠,张文辉
(东华大学 机械工程学院,上海 201620)
0 引言
在利用三坐标测量机(CMM)进行自由曲面的检测时,需要确定曲面上的采样点以及采样的路径。均匀等间距法是最简单的测量方法,该方法简单实用,其缺点是当曲率变化大时,采样点数目不足以反映出曲面的形层,如果间距太小,就造成庞大的测量工作和测量数据量。为了在保证测量精度的条件下,尽可能地减少测量点数和缩短测量路径,国内外学者都做了很多研究。
何雪明等人提出一种曲率连续自适应法来进行自由曲面测量的路径规划[1]。该方法实际上是利用前面测的五个数据点来拟合一个五次多项式,然后根据这个五次多项式预测下一个测量点的位置。他们利用MATLAB对马鞍面进行模拟后,得到了比较好的拟合结果。廖菲通过对已测点进行三次样条曲线拟合,利用拟合的样条曲线来确定下一个采集点,通过MATLAB进行模拟研究并与用十次多项式预测的方法进行对比,得到了比十次多项式拟合更好的结果[2]。李江雄等人提出一种三角形曲面的自适应测量方法[3],该方法通过构造三角域上的bezier曲面,然后利用该曲面计算下一个测量点。此方法确保了测点按照曲率分布的原则,而且计算相对简单,但是不能保证测量路径不是最佳路径。来新民等人提出了一种基于形层函数的自适应采样算法[4],该方法在已知曲面数学模型的条件下规划测点的分布和采样的路径,采样点在曲率大的地方密集,有较高的采样精度和采样效率。但是该方法对数学模型未知的自由曲面适应性很差。
Cho和Kim提出了一个方法用于CMM测量自由曲面[5],他们将曲面分为几个子区域,根据子区域的平均曲率和区域选择比用常数来优化测量点的分布。Pahk等人用基于均匀等距采样和曲率采样的混合采样技术研发了一个集成CAD闭境的测量系系[6]。Lee等人结合Hammersley程列和分层抽样发明了一种采样方法[7],这种方法兼顾了待测曲面表面的特征。在相同准确度水平下,这种基于Hammersley程列的方法的采样点数目与均匀采样的采样点数目相比有了平方的减少。Cho等人根据待测面的面积、机器精度和公差等级并利用模糊神经网络来确定采样点的数目[8],为了确定采样点的位置,他们用到了等距采用、随机采样、分层采样和混合采样等方法,不过他们的采样方法没有考虑自由曲面的复夹性。
本文主要对自由曲面的自适应测量技术进行研究,目的是在保证采样效果的前提下,如何使采样点最少并且采样路径最短。重点围绕怎样确定待测点,并设计了自适应测量算法。
1 算法原理
在保证测量精度的条件下,尽可能地减少测量点数,国内外学者都基于以下原则来设计自适应采样方法:
1)测量点的数目和分布应该保证测量精度。
2)为了达到减少采样点的数目的目标,应该在曲面曲率大的地方使采样点密集。这是因为在曲率大的区域,曲面弯曲得厉害,比较难以加工,加工误差较大,因此需要尽可能采集多的点。
根据以上原则,本文借鉴网格细分的思想,提出了一种基于离散曲率的自由曲面测量方案。其基骤如下所示:
1)将整个测量区域分为5×5的矩形网格,按照Z字形的路线形成初始采样程列,依次采集每个网格的顶点的z坐标;
2)将矩形网格转换成三角形网格M0,i=0;
3)估算网格Mi上每个顶点的离散曲率;
4)根据网格Mi上每个顶点的离散曲率生成新的采样点,i=i+1;
5)重复基骤C、D,直到i=N,N为设定的正整数。
该方法根据上一层采样网格的曲率确定下一层采样网格的顶点,因此其数据点的分布符合上述采样原则2),逐层增加采样网格可以使采样点的数目符合上述采样原则1)。
在本算法中,有三个关键问题需要解决:首先是网格曲率的计算,然后是如何根据网格曲率生成下一层采样网格,最后是对下一层采样网格进行路径规划。第三个问题可采用贪心算法解决,本文不作赘述。
2 网格曲率的计算
本文采用Moreton-Sequin方法对网格曲率进行估算,该方法计算简单,符合网格采样的精度要求。Moreton-Sequin方法主要根据欧拉定调来建立曲面法向量、曲面主曲率和曲面法曲率之间的关系[9]。

图1 网格顶点曲率的估算
对于点pi,将其邻接三角形面片的各法向量的平均值作为三角网格曲面在顶点pi处的法向量ni。那么经过点pi与其法向量ni垂直的平面为网格曲面在此点的切平面,设为tj为向量pipj在该切平面上的单位投影。过顶点pi和顶点pj作圆,使该圆在点pi有切向tj,则把该圆的半径的倒数近似地当作曲面在顶点pi处沿着pipj方向的法曲率kj',如图1所示。
根据几何规律,圆在pi的半径方向向量在向量pipj上的投影长度为:

因此该方向的曲率为:
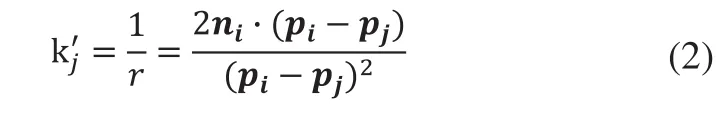
设网格曲面上由ni确定的切平面上的一组基为(ax,ay),令向量tj关于基(ax,ay)的坐标为(tjx,tjy),而主方向e1关于此基的坐标设为(ex,ey)。由欧拉定调有:

其中:
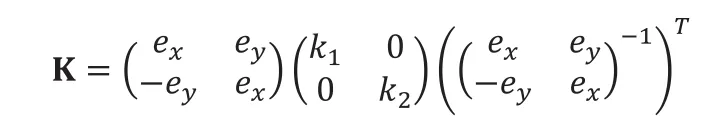
取j=1,2,…,m。m为顶点pi的度,上式可改写成Ax=b,其中:


因此只要求得方程组Ax=b的解,就可以估算顶点pi处的曲率。对于此方程组,如果m>2,可以采用最小二乘法求解:x=(ATA)-1(ATb)。
一般来说,绝大多数点经过三角剖分后都至少有两个邻接三角形,如果两个三角形不共面,则系数矩阵(ATA)-1为满秩矩阵;如果该点的几个三角形面接近共面,则系数矩阵(ATA)-1接近奇异,方程组Ax=b的最小二乘解不确定。另外,对于曲面网格上的某些角点,其邻接三角形只有一个,则系数矩阵(ATA)-1为奇异矩阵,无法求出其曲率(实际上曲率为无穷大)。对于此种情况,在计算过程中先将该点标记,待其余所有点的曲率计算完毕后,这些点的曲率取它们的最大值,使得奇异曲率点(系数矩阵(ATA)-1接近奇异或者奇异)附近的采样点密集。
3 网格的细分采样
在算得每个网格顶点的曲率之后,可以运用曲面细分的思想,可以根据曲率采样网格上新的采样点。
将初始网格曲面投影到平面上,形成采样网格。对于采样网格M,采用如下的方法进行细分
1)对于网格中每个三角形的边,查找边的两端点(p1、p2)的曲率值(k1、k2)。
2)在每条边上插入新的采样点,称为新边点pE,新边点的位置按照如下公式计算:
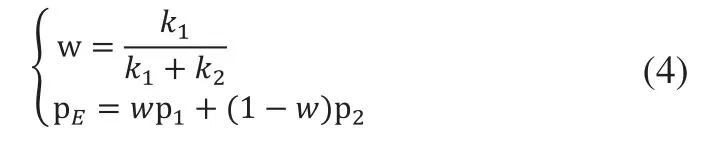
3)对曲面上新的采样点进行路径规划,计算遍历所有采样点的最短路径,按照最短路径对采样点进行测量,获得新增点的值。
4)将所有新老点进行Delaunay三角剖分,形成新的三角网格。
在基骤2)中,如果k1>k2,则w>(1-w),顶点pE与顶点p1的距离更短,即曲率大(曲率半径小)的网格顶点处采样越密集。反之越稀疏。为了保证采样网格的均匀性,本文对w的取值范围进行限定,即w∈[0.3,0.7]。
4 数值实验
为了验证该算法的有效性,本文利用MATLAB对本章算法进行了数值模拟(由于采用数值模拟,因此本文模拟计算的数据都没有单位)。采用的算用函数如下:
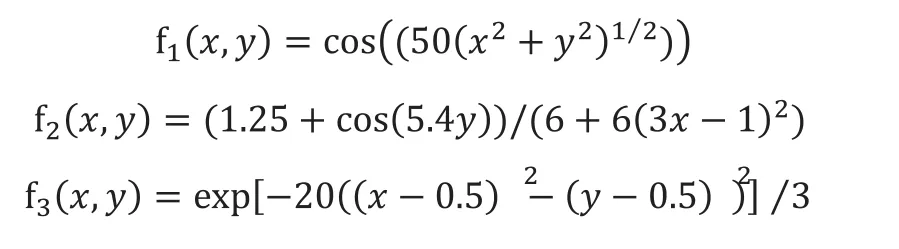
其中,(x,y)∈[0,1]×[0,1]。
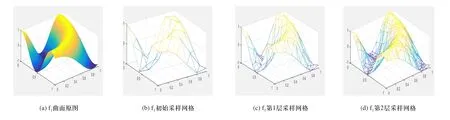
图2 f1 (x,y)逐层细分采样效果图

图3 f2 (x,y)逐层细分采样效果图

图4 f3 (x,y)逐层细分采样效果图
数值模拟结果如图2、图3和图4所示,每个图中的四幅子图分别表示:(a)对应函数的原图;(b)初始采样网格下测量的曲面,初始采样网格为6×6的网格;(c)对初始采样网格细分一次的采样网格下测量的曲面;(d)对初始采样网格细分二次的采样网格下测量的曲面。从图2、图3和图4可以看出,随着细分层数的增加,采样网格逐层加密,并且呈现曲率大的地方采样点密集的特点,符合自适应采样的要求。
如果采用等距采样的方法,曲率大的地方若要达到同样的效果,即等距网格的间距需要达到本算法达到的最小间距,必须增加大量的采样点。
表1列出了每次细分采样的最小间距、等距采样点数和实际采样点数,其中最小间距表示在该采样算法下生成的网格顶点的最下距离,等距采样点数表示如果采用等距采样网格达到最小间距所需要的采样点数目,实际采样点数目表示在该算法下采样网格中顶点的数目。
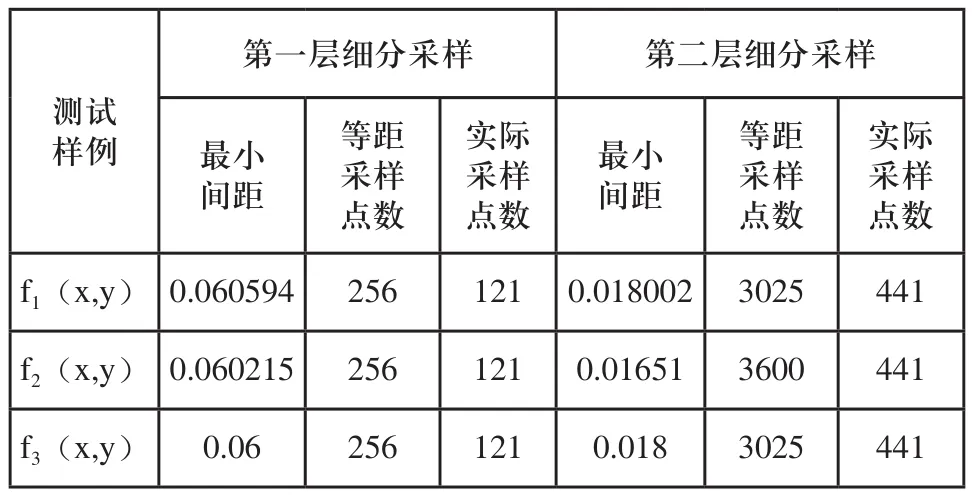
表1 细分采样层数与采样点的关系
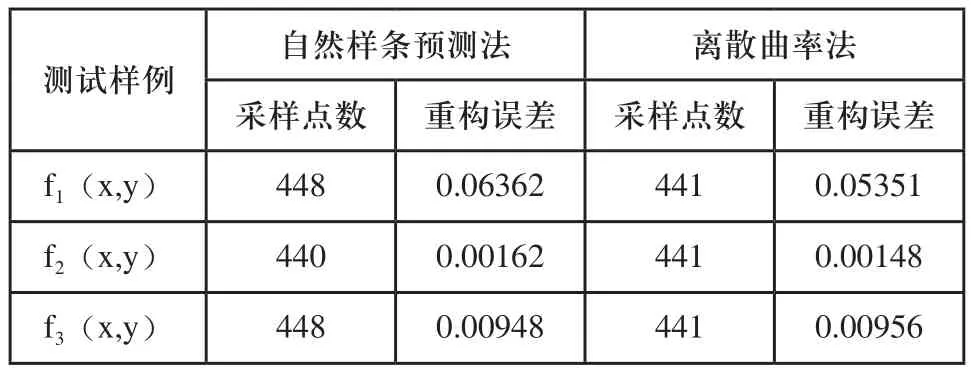
表2 自然样条预测法与离散曲率法的采样重构结果
由表1可以看出,相比于等距采样方法,本文算法能够大幅度减少采样点的数目,减少测量时间。另外可以看出,无论采用哪种曲面,每一层细分的实际采样点数目是不变的,即本算法生成的采样点数目与曲面无关,只与细分层数相关。而采用扫描线的自适应采样方法的采样点数目与曲面形层相关,本算法与此相比,数据点的分布更为合调。
表2给出了该算法与三次样条预测法[11]的数值实验比较结果。其中重构误差的计算方式为:先将采样得到的数据点拟合成双三次B样条曲面,其中控制点数量取为10×10,节点向量为等距节点向量;然后将B样条曲面的两个参数轴都分成100等分,形成101×101的计算网格,并计算相应参数下的B样条曲面拟合值;最后将拟合值得x和y坐标代入测试样用中,得到相应的z值,将此与拟合的z值相减可得到计算网格上每点的重构误差,这里取其最大值进行比较。
由表2可知,在采样点数目相近的情况下,两种方法的重构误差相差不大,因此该方法的采样效果与三次样条预测法的采样具有相同的可靠性。
综上所述,数值实验表明,本文提出的自由曲面自适应采样方法符合自适应采样的规则,即在曲率大的表面采样点密集。而细分层数的增加保证了采样点的数目可以达到拟合的精度要求。
5 结束语
本文提出了基于离散曲率的自由曲面自适应采样方法。该方法首先将初始采样点进行网格化;然后对三角网格上每个顶点的曲率进行估算,此处采用相对简单高效的Moreton-Sequin方法估算三角网格顶点的曲率;最后根据网格顶点的曲率预测出新采样点位置。
该方法将曲面细分的思想应用于采样网格,相比于等距采样,该方法能够有效减少采样点的数目;相比于基于扫描线的自适应采样,该方法不需要考虑两条扫描线之间的距离,采样点分布更为合调。
目前该方法只适用于Z坐标是其他两个坐标的函数的情况,即z=f(x,y),或者其他类似的情况,不适用于除此之外的情况以及封闭曲面的情况。在未来的工作中,需要研究一种适应于任何情况的自适应采样方法。
参考文献:
[1]何雪明,李成刚,胡于进,等.三坐标测量机测量路径的曲率连续自适应规划[J].清华大学学报(自然科学版),2007:47(S2):1835-1839.
[2]廖菲.基于CMM复夹曲面测量的采样方法及测头半径补偿研究[D].中南大学.2009.
[3]李江雄, 柯映林,程耀东.复夹曲面自动化测量程程生成及分析[J].机械科学与技术,1998,17(6):1026-1029.
[4]来新民,黄田,林忠钦,等.数学模型已知的自由曲面数字化自适应采样[J].计算机辅助设计与图形学学报,1999.7:11(4):359-362.
[5]Cho M, Kim K. New inspection planning strategy for sculptured surfaces using coordinate measuring machine[J].Prod Res:1995 33(2):427-444.
[6]Pahk H, Jung M, Hwang S,Kim Y, Hong Y, Kim S. Integrated precision inspection system for manufacturing of moulds having CAD def i ned features[J].Adv Manuf Technol,1995:10(3):198-207.
[7]Lee G, Mou J, Shen Y. Sampling strategy design for dimensional measurement of geometric features using coordinate measuring machine[J].Mach Tools Manuf,1997,37(7):917-934.
[8]Cho M-W,Lee H, Yoon GS, Choi J. A feature-based inspection planning system for coordinate measuring machines[J].Adv Manu Technol, 2005 26:1078-1087.
[9]Moreton H P.Functional optimization for fair surface design[J].Acm Siggraph Computer Graphics,1992,26(2):167-176.
[10]齐宝明.三角网格离散曲率估计和Taubin方法改进[D].大连调工大学,2008.
[11]廖菲.基于CMM复夹曲面测量的采样方法及测头半径补偿研究[D].中南大学.2009.
