XFEM及其在正交异性钢桥面板疲劳裂纹扩展中的应用
2018-04-13顾安邦杜柏松
渠 昱,曾 勇,顾安邦,杜柏松
(1.重庆交通大学 山区桥梁与隧道工程国家重点实验室培育基地,重庆 400074;2.重庆交通大学 山区桥梁结构与材料教育部工程研究中心,重庆 400074)
线弹性断裂力学的主要任务是计算裂纹扩展长度、扩展率和能量释放率。裂纹扩展计算比较困难,对于复杂结构更困难,它涉及断裂力学、材料科学和计算方法等学科。在有限元(FE)中,裂纹计算要求有限单元边界与裂纹对齐,裂纹扩展需要不断地更新网格,诸如可视化后处理技术等计算方法需要对网格演化进行大量计算,因此采用普通有限元方法(FEM)计算裂纹扩展遇到极大挑战,限制了有限元的应用。
1 扩展有限元(XFEM)
XFEM最有吸引力的是将不连续问题加入到有限元而又不要求网格与不连续函数及其导数一致,从而避免了重新划分网格。在许多情况下,避免网格重划分方法是可取的,可以减少大量的网格演化等计算[1]。XFEM是一个非常灵活的方法,其基本想法是将不连续位移场矩阵分解为2部分:uh(X)=ucont(X) +udisc(X),连续部分ucont(X)是标准有限元插值矩阵,不连续部分udisc(X)是根据局部单位分解定理[2,3]增加的部分(即富集),并将这些富集信息嵌入有限元插值。所谓富集是将额外的未知量浓缩到单元水平,这样的矩阵仍然是稀疏的,因此可以用现有的有限元分析框架处理不连续问题。
当裂尖位移场已知,基于渐进场的富集函数可以被添加到近似解空间中。对于裂纹和位错奇异的渐进场,可以作为裂尖区和位错核的富集函数,从而大大减少了在子域细化网格的工作量,XFEM已成为断裂分析最流行的方法。
这些方法在解决材料科学问题上的主要优点是对不连续现象建模简化。在传统的有限元方法中,划分网格时必须使单元的边缘/面与裂纹重合、在裂纹每一侧布置节点,才能考虑材料沿裂纹面的分离。这样的网格创建相当困难,特别是三维问题,因为网格还必须考虑到模型的其它特性,如晶界或夹杂物。在XFEM中,沿裂纹面不连续位移场的引入是通过添加基函数来创建近似解,摆脱了网格的约束。当XFEM与水平集方法LSM(level-set method)相结合,就可以在原来有限元节点上用节点值完整表达诸如裂纹的几何形状和位移场等特性。同样,相边界和其他不连续性的模拟,也可以用这种方法。特别是当几何形状演化、裂纹扩展或移动相边界,这些优点是非常重要的。
1.1 XFEM中的裂纹的描述
裂纹采用2个水平集函数描述[3-5]:
1) 描述裂纹路径Γα的水平集函数f(x),即有向距离函数:
(1)
2) 定义裂纹位置的水平集函数g(x),原点在裂尖,方向与裂纹垂直。该函数定义的坐标系见图1(b),坐标系中的r和θ定义为:
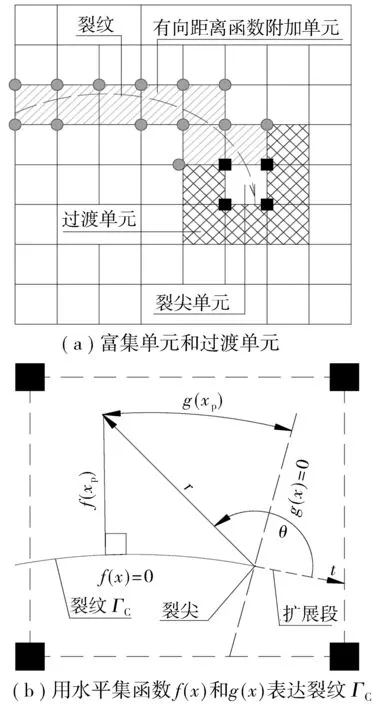
图1 富集单元、过渡单元和水平集函数Fig. 1 Enrichment unit,transition unit and horizontal set function
与一般闭合面相比,裂纹属于开放界面,2个水平集函数f(x,t)和g(x,t)分别描述裂纹面和裂尖。点x位于裂纹面上的条件是f(x,t)=0,g(x,t) > 0;位于裂尖的条件是f(x,t)=0,g(x,t)=0。裂纹问题的另一个特点是,某位置一旦成为裂纹的一部分,则一直保持为裂纹的一部分。因此裂纹扩展时,只需要更新水平集函数f(x,t)以及g(x,t) 在裂尖的位置,而f(x,t) 在裂尖后面的位置保持不变。等于0的水平集称为零水平集,用于描述裂纹面。裂尖后面的零水平集不必更新,从而避免了差分方程的麻烦。在界面的法向方向移动,水平集函数不需要随界面运动速度更新,因此,不使用Hamilton-Jacobi方程更新;反之,水平集函数随裂尖的速度运动需要更新。
水平集方法简单、有效和便于实现,XFEM与水平集相结合,功能更强大,因为这样描述裂纹、位错、晶粒边界和位相界面可以严格用节点表达,而且能利用水平集这个强大的工具跟踪这些表面的演化。
1.2 XFEM中的富集函数
在XFEM中,单元被裂纹切割有2种情况:① 被裂纹完全切割的单元称为裂纹体单元;② 含有裂尖的单元称为裂尖单元。裂纹体单元节点富集采用有向距离函数式(2),裂尖富集函数是基于裂尖场的渐进解。对于线性断裂力学,取分支函数(整体函数)为富集函数[6]:
(2)
式中:r、θ为原点定义在裂尖的局部极坐标。
1.3 XFEM中的过渡单元问题
与总体富集方法相比,T. BELYTSCHKO等[3,4]介绍的富集函数局部单位分解能减少未知数量,改进数值计算条件。
J. CHESSA等[7]认为:在富集和非富集单元之间存在过渡单元产生多余项问题,近似解空间的多余项是引起误差的根源。对于采用有向距离函数式(2)作为富集函数的过渡单元边上,富集函数为0,因此不会产生多余项。但是对于裂尖富集,XFEM的过渡单元〔图1(a)中交叉线所示〕 中只有2个节点被富集,形函数就不再满足单位分解条件[8],过渡单元会产生多余项,从而降低数值算法的收敛性。
例如:如果富集节点集I*中只有一个过渡单元,这个单元的近似解为:
(3)

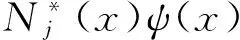
N. SUKUMAR等[8]发现,采用背脊型的富集函数,过渡单元会产生误差,从而降低数值算法的收敛性。修正的背脊型富集函数能改进其收敛效率。J. CHESSA等[7]通过进一步的研究,提出假设应变法以消除过渡单元的多余项。这个方法的缺点是需要特殊的假定应变单元,而该单元又取决于富集函数和单元类型,需要逐点构建。富集函数构造困难,且不具有通用性。
对于裂尖单元,过渡单元的多余项限制了局部单位分解精度。T. P. FRIES[9]提出了斜坡函数法来解决过渡单元多余项的影响。其主要缺点是:① 裂尖过渡单元富集节点为16个,多于XFEM的4个;② 自由度大约是XFEM的3倍;③有缺秩问题,富集矩阵的秩是16,而线性无关的条件只有14。
2 不连续伽辽金XFEM(DG-XFEM)
另一个避免过渡单元多余项的方法是利用内罚函数方法[10],使富集和不富集区域之间强制连续,称为DG-XFEM[11]。该方法比标准XFEM更精确,收敛速度得到了优化。
在基于分片区域的DG-XFEM方法中,域被分成几个不互相重叠的区域,对这些区域分别进行富集并用内罚函数强制区域之间连续。该方法的最佳特性是富集是局部的,且所有的形函数满足单位分解。为简单计,笔者只论述平面二维的情况,该方法同样适用于三维平面裂纹。
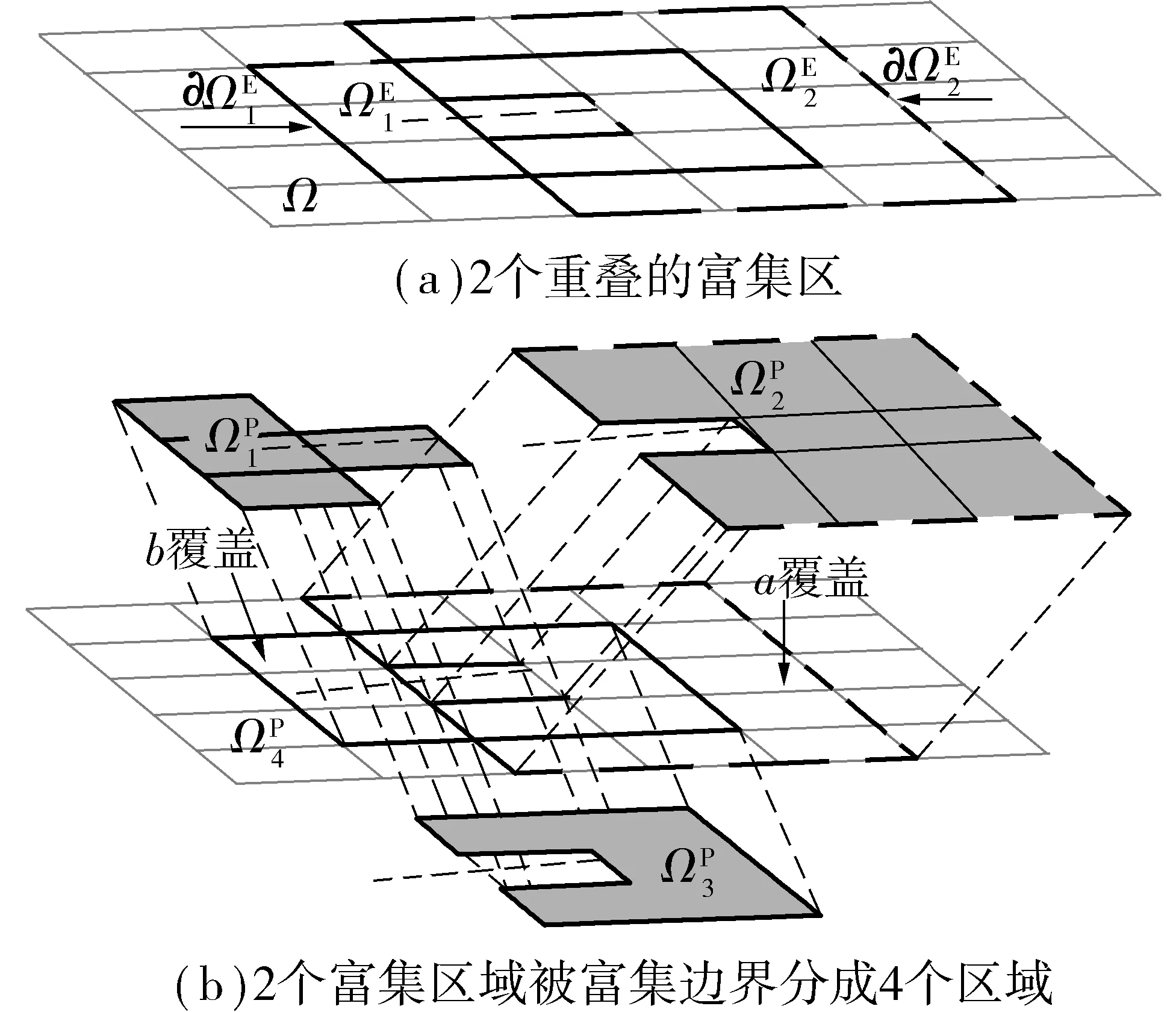
图2 富集区域划分示意Fig. 2 Enrichment region division
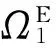
(4)

覆盖重叠之间用内罚函数强制连续。通过弱不连续变分,得到过渡单元的刚度矩阵
(KXFEM+KDG)d=fext
(5)
式中:KXFEM为每一个覆盖的标准XFEM刚度矩阵的集成;KDG为重叠覆盖部分强制连续的不连续伽辽金(DG)项,是刚度的修正项;fext为节点力。
域Ω被分成np个互相不重叠的覆盖(Ωb)P,b=1~np,b覆盖中I节点向量为:
(6)
(7)
(8)
式中:a为罚函数;因子μ=1;dT为节点自由度向量。
采用适度的内点罚函数值,方程(5)受损不明显,线性系统方程组的迭代方法解仍然有效:
(9)
(10)
(11)
(12)
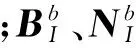
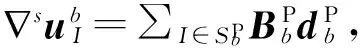
从而,可由没有富集的有限元、完全富集的XFEM和过渡单元构成求解域的离散方程(5)。
DG-XFEM验证:选择桥梁钢板Q370qE、单边拉伸的边裂纹情况对DG-XFEM进行验证。
钢板长L=5 m,宽W=1.5 m,板厚d=0.01 m。利用XFEM计算得到沿裂纹面的应力sxx和syy分布情况,并与Westergaard应力函数[12]计算的理论结果进行比较(图3)。可以看出,二者符合很好,在过渡单元没有出现数值不收敛的情况。
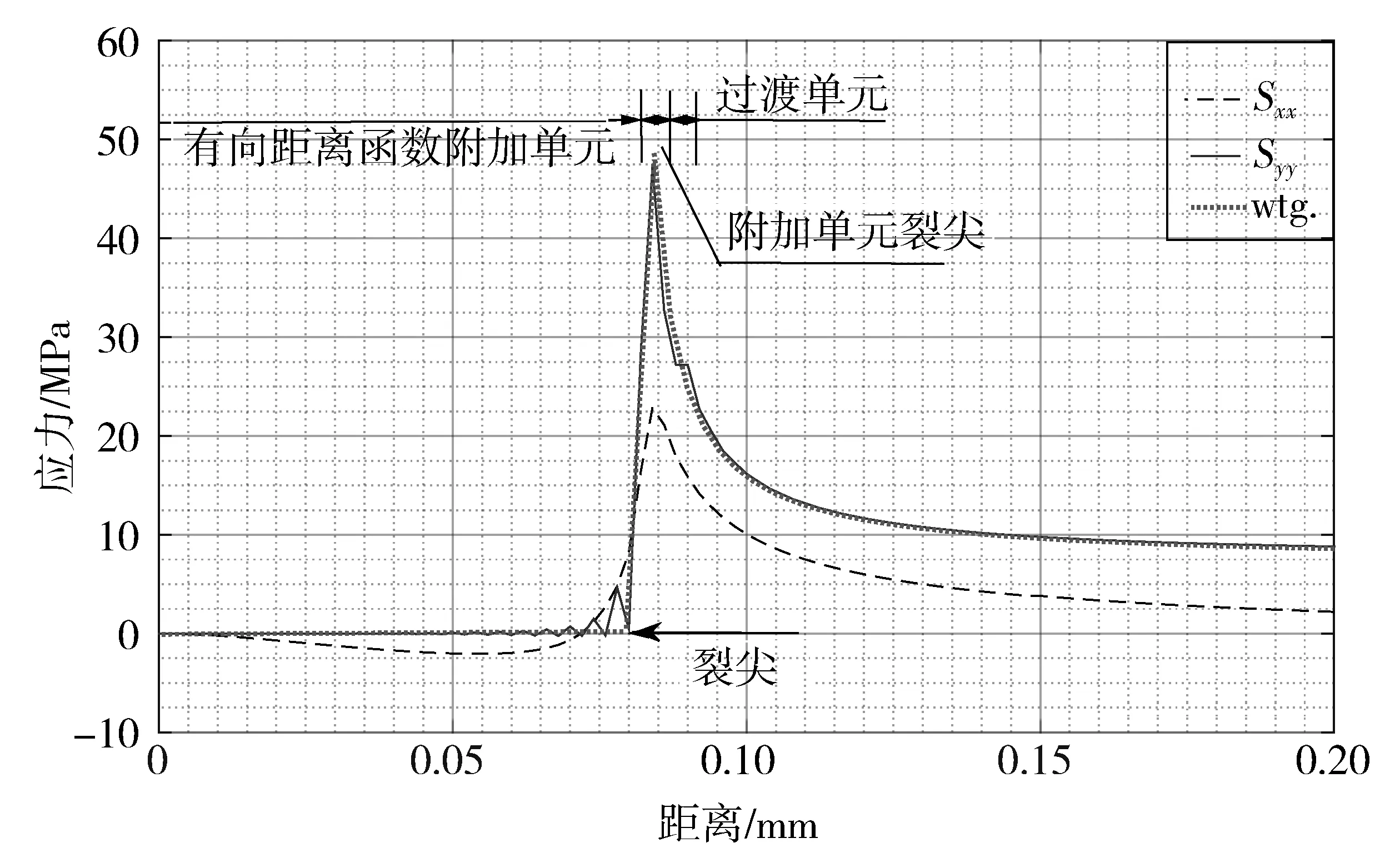
图3 钢板边裂纹计算的沿裂纹面应力分布及理论值比较Fig. 3 Comparison between the calculated crack surfaces stress distribution and theoretical values of the steel plate with side crack
3 DG-XFEM在正交异性钢桥面板疲劳裂纹扩展中的应用
3.1 模型试验
以某长江大桥为试验背景。该桥为主跨长788 m的钢箱梁悬索桥,吊索间距16 m,加劲梁为流线型扁平钢箱梁,梁高3.5 m,主桥宽27.5 m;每一节段顺桥向5个横隔板,间距2.7 m,横向共40个U肋,间距0.6 m。
在钢桥面板模型设计过程中,按弹性支撑连续梁、利用有限元对实桥整体进行了仿真模拟。根据整体分析,选择长16 m标准节段的钢箱梁,按弹性简支进行有限元分析。根据节段钢箱梁的分析结果和正交异性板各疲劳细节仅对轮载敏感的局部特性[13],按照1∶2的比例尺建立简化面板节段模型,横向包括7个闭口U肋,纵向3个横隔板,按纵向简支、横向仅限制向下的位移条件进行试验[14]。
试验的疲劳荷载是根据三峡库区的实际交通状况,按照JTG D64—2015《公路钢结构桥梁设计规范》[13],参考AASHTO规范[15]的单车模型,考虑1.15的冲击系数,按1∶2比例模型和等效应力脉换算得到轴载47.7 kN,在1 000 kN的MTS机上进行。二期恒载15 kN,汽车活载47.7 kN,均通过MTS机加载。考虑铺装效应,荷载通过分力桥施加。
在试验中,当加载2.0×106次循环时,6 # 弧形开孔出现7.5 mm长的裂纹,2.2×106、2.4×106次循环加载时裂纹分别扩展到12、21 mm,在2.6×106次终止试验时裂纹扩展到31 mm(图4)。

图4 6 # 开孔处疲劳裂纹试验照片Fig. 4 Photo of fatigue crack in right side of 6# hole
3.2 数值模型
根据试验模型的尺寸和约束条件,利用Abaqus平台创建3-D不连续有限元模型,面板节段模型见图5,划分节点383 344个,C3D8R单元190 791个,裂纹体单元采用有向距离函数富集,裂尖单元采用分支函数富集,富集单元和过渡单元的边界采用内点罚函数方法强制连续,采用DG-XFEM进行计算。
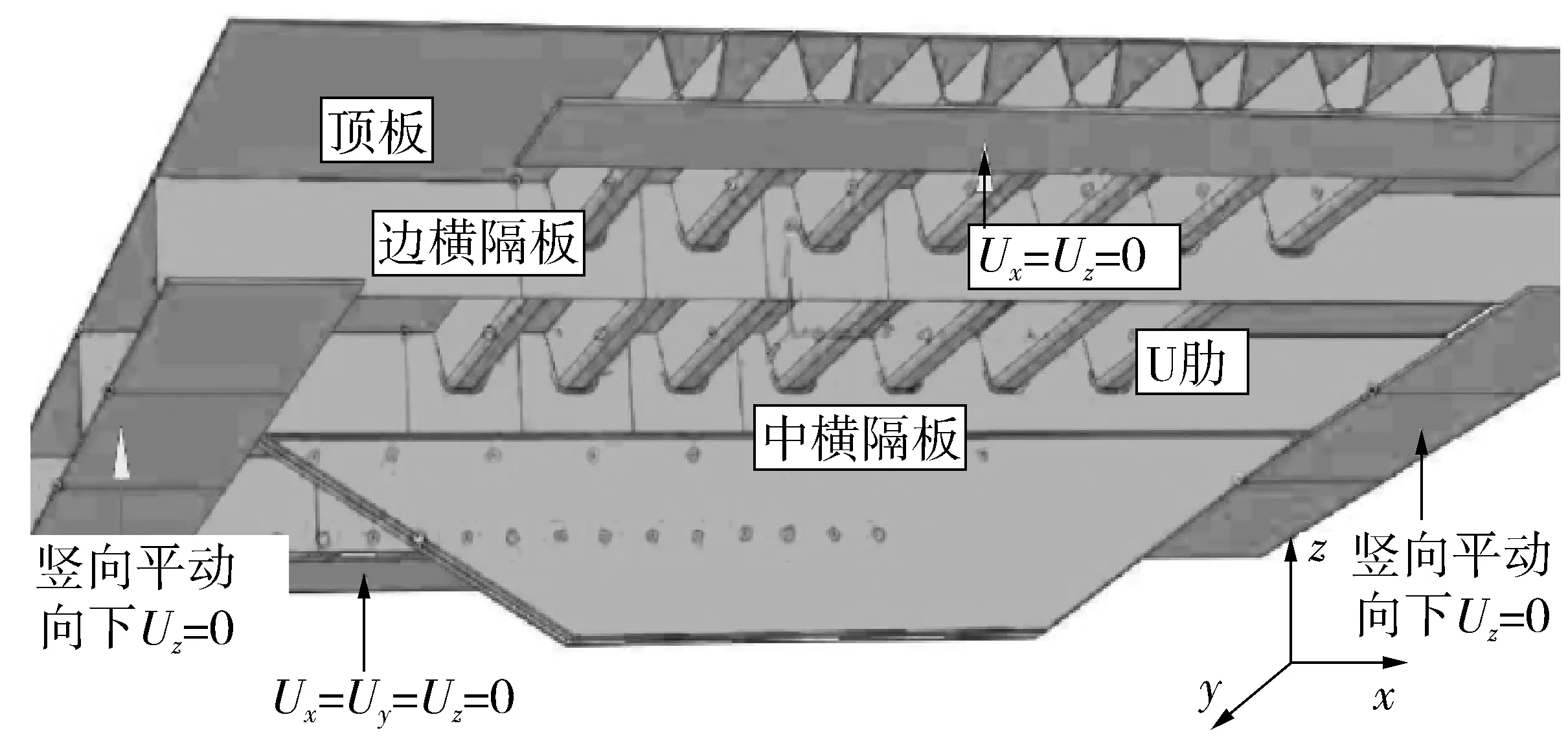
图5 钢箱梁节段面板模型Fig. 5 Segment deck model of steel box girder
在有限元分析中假定材料为理想线弹性的,14MnNbq桥梁钢板材,弹性模量E=2.1×105MPa,屈服强度σy≥370 MPa,断裂强度σb≥530 MPa,泊松比为ν=0.3,V型冲击功JV≥41 J,粘性裂纹分片连续,基于损伤演化方法进行数值分析。
损伤判据为最大主应力失效准则。正交异性钢桥面板各个疲劳细节的常幅疲劳极限不尽相同,裂纹出现在横隔板挖孔处,疲劳细节的常幅疲劳极限为70 MPa[13],超过该值即产生裂纹。
根据损伤力学原理,裂纹在开裂和扩展过程中,在裂尖及其周围的材料处于塑形状态,再应用弹性材料计算就不合适了,因而采用塑形材料参数进行数值模型设置。在模型试验中裂纹萌生和扩展采用的是应力和加载次数来体现,而在数值模拟中,加载次数不容易实现,所以采用能量原理,用法向断裂能42.2 kN/m判断裂纹是否扩展,扩展方向为切应力最大的方向。损伤稳定系数DS=5.0×10-5,用于判断裂纹是否止裂。
目前裂纹扩展研究还必须将裂纹分成微观阶段和宏观阶段2个阶段:
1) 疲劳是一种对微观结构非常敏感的现象。由于微结构的易变性,裂纹萌生阶段的长度与晶粒主尺寸相当,以张开(Ⅰ型裂纹) 和滑移(Ⅱ、Ⅲ型裂纹)相结合的形式生长,沿最大分切应力滑移系统扩展。最大分切应力逐点不同,扩展路径弯曲,因此不稳定、不规则,不能用断裂力学研究。材料的生产、制造和热处理过程的结果,使测量的损伤趋势具有相当大的不确定性[16],即使对于相同的材料也是如此。
2) 宏观裂纹扩展不受材料微结构的影响,可以用Paris定律表达。要计算裂纹扩展,首先必须确定初始裂纹长度。M.H.EL-HADDAD等[17]建议使用长裂纹应力强度因子门槛值ΔKth和虚拟裂纹长度a0表达疲劳极限σf:
(13)
式中:Y为几何形状系数,取决于裂纹的几何形态,对于穿透裂纹(长度2a)无限平板Y=1.0,其它裂纹类型,Y值可以从应力强度因子求解。
式(12)中的虚拟裂纹长度a0即为相当初始裂纹长度。相当初始裂纹是指满足Paris定律的最小宏观裂纹,是为了避免微裂纹扩展不稳定和不规则问题而提出的。工程中常根据经验假定初始裂纹长度,如金属假定1~3 mm量级,或者利用无损探伤的结果来确定。对于桥梁钢Q370qE,根据文献[18]:
ΔKth=5.556(1-0.825R)1.147
(14)
式中:R为加载应力比。
由文中试验应力比R=0.221 5,得到ΔKth=4.408 MPa·m0.5。根据式(11)得到初始裂纹长度为1.26 mm,以此作为文中裂纹扩展的相当初始裂纹长度。
根据模型试验结果,利用所建立的有限元模型进行整体分析,得到的6#孔左侧(PEL) 和右侧(PER) 周边单元主应力分布,如图6。
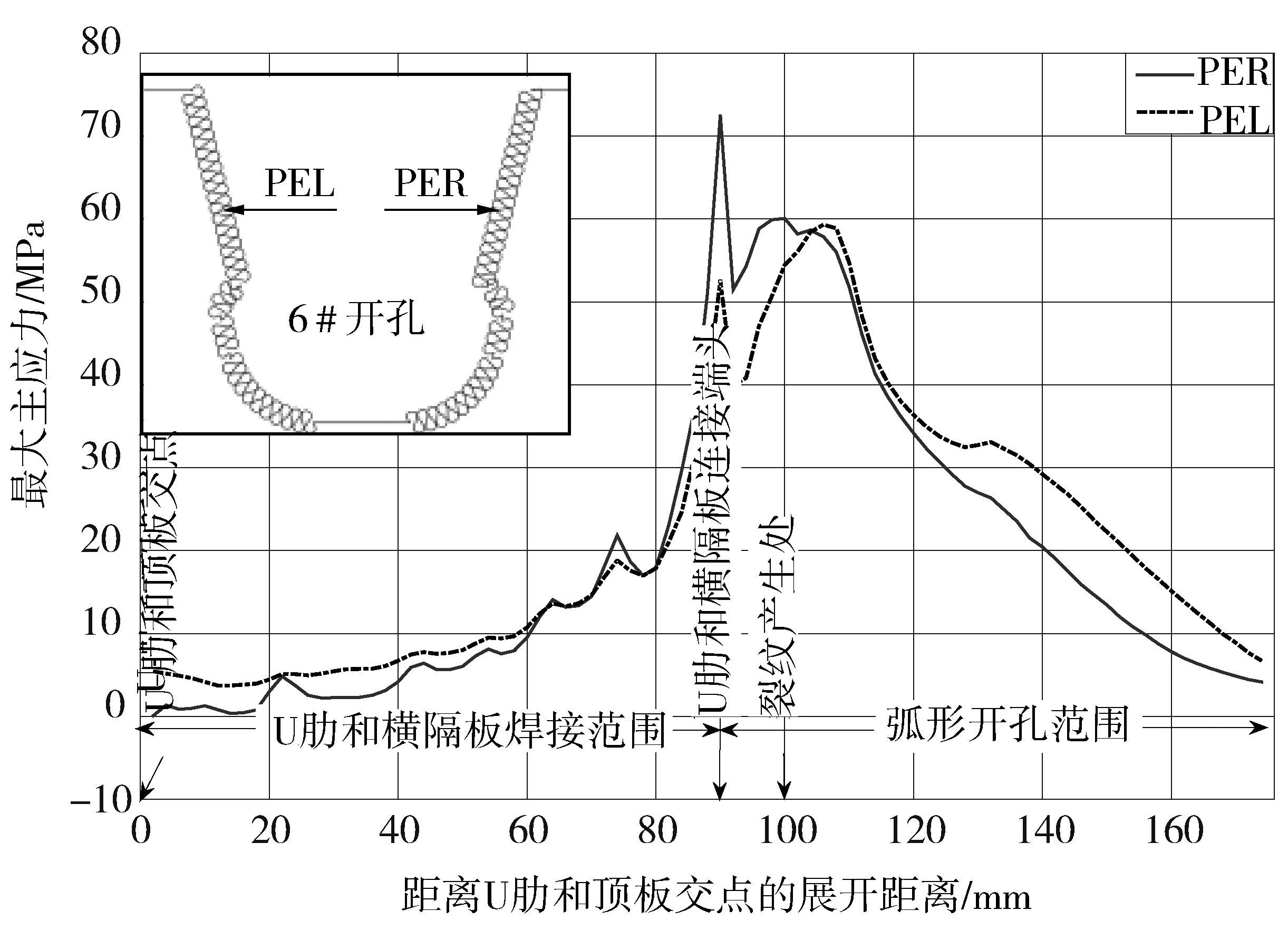
图6 横隔板6 # 开孔周边单元主应力分布Fig. 6 Principal stress distribution of perimeter elements of 6# hole at diaphragm
从图6可以看出,横隔板6 # 开孔最大主应力超过60 MPa,热点应力系数取1.3进行计算[19],主应力为78 MPa,超过该疲劳细节的常幅疲劳极限70 MPa。考虑到应力集中、焊接缺陷和焊接残余应力的影响,正交异性钢桥面板横隔板开孔区是疲劳裂纹多发区域,为对疲劳最敏感的区域。根据李传习等[19]对某扁平钢箱梁大桥裂纹统计研究,出现在横隔板开孔区域和U肋与横隔板焊接端头的裂纹占全桥裂纹总数的89.4%。
根据数值分析结果,绘制5 #、6 # 开孔之间的横隔板在没有裂纹情况下的主应力等值线,如图7。
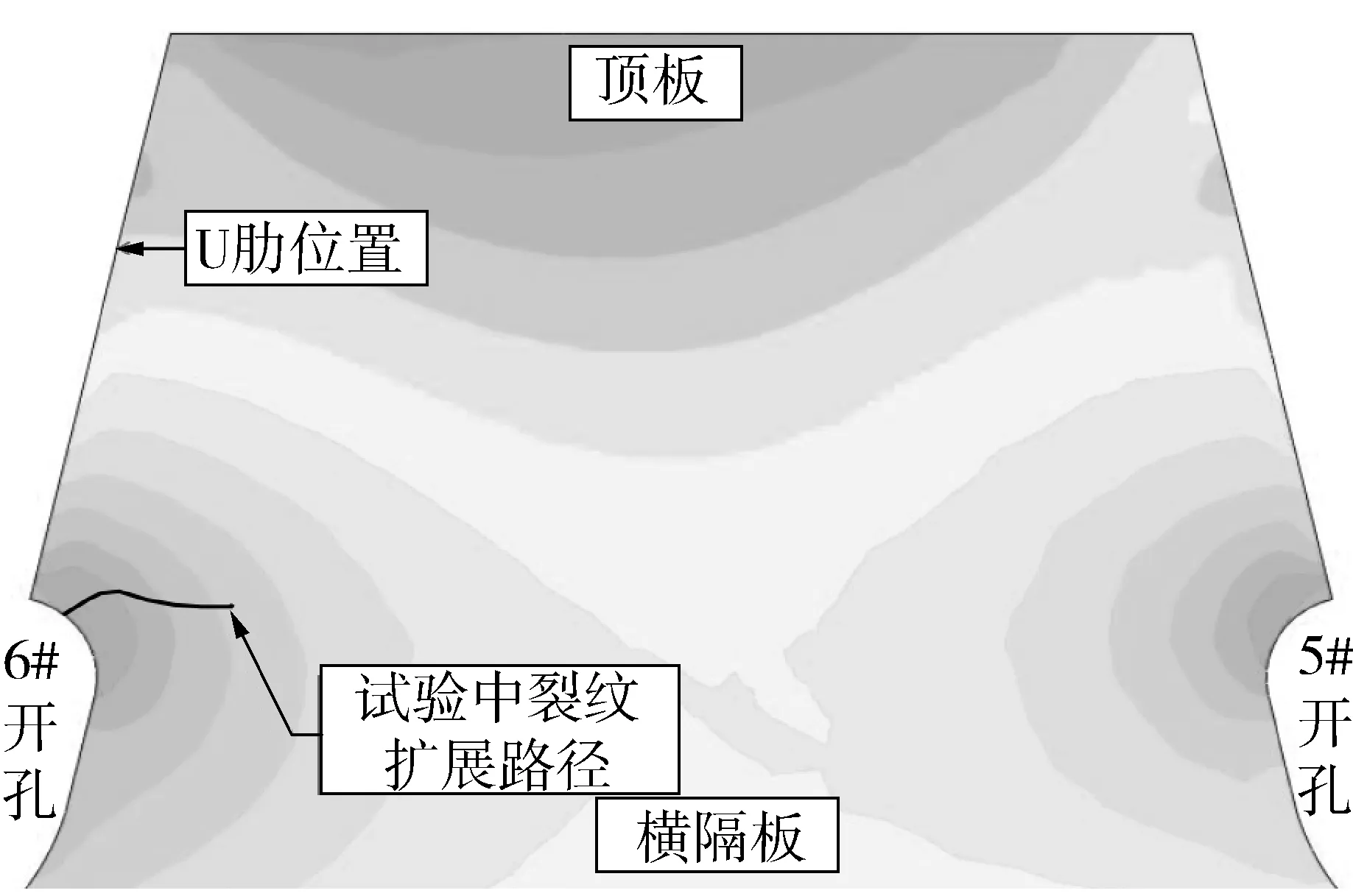
图7 横隔板5#、6#孔之间的无裂纹主应力等值线Fig. 7 Principal stress isocline between 5# and 6# holes calculated by XFEM without crack
从图7可以看出:
1) 开孔周边的应力高、裂纹产生处的应力超过该疲劳细节的常幅疲劳极限,应力梯度陡,越往两孔中间应力越低。
2) 两开孔之间的水平区域均为高应力区,裂纹在此区域产生并沿水平方向扩展,以保证裂纹尖端获取足够的能量维持扩展,随着应力强度减弱,裂纹扩展逐渐停止。
3) 裂纹在初始阶段垂直于应力等值线、沿最大主应力方向向板内扩展,这与裂纹扩展的基本理论一致。
从图4、图8可以看出,2.6×106次循环试验结束时裂纹扩展长度为31 mm(图4),计算值为32.3 mm〔图8(a)〕,二者相差很小。数值模拟中裂纹出现的位置、扩展路径和长度与试验结果符合很好。也与实桥横隔板中出现的裂纹基本一致〔图8(b)〕[20]。

图8 横隔板开孔处计算的裂纹扩展与实桥裂纹扩展比较Fig. 8 Comparison of crack growth calculated at diaphragm and that of real bridge
4 结 论
1) 利用平板单边裂纹的应力函数理论解对DG-XFEM进行验证,结果表明DG-XFEM能很好地解决过渡单元引起的数值收敛效率问题。
2) 利用XFEM得到的应力场,分析表明:弧形开孔处是高应力区,与几何不连续造成的应力集中、焊接缺陷和残余应力的作用叠加,形成疲劳裂纹的高发区域,是正交异性钢桥面板对疲劳最敏感的部位。
3) 利用DG-XFEM模拟裂纹扩展,分析表明:裂纹扩展的初始阶段与主应力等值线垂直,且沿水平方向的高应力区向板内扩展,以保证裂尖获取足够的能量维持裂纹扩展,随着应力强度减弱,裂纹扩展逐渐停止,裂纹扩展路径与试验和实桥出现的情况一致,也与裂纹扩展的基本理论一致,证明了利用DG-XFEM对正交异性钢桥面板疲劳裂纹扩展分析的有效性和合理性。
参考文献(References):
[1] RABCZUK T.Computational methods for fracture in brittle and quasi-brittle solids:State-of-the-art review and future perspectives[J].ISRNAppliedMathematics,2013,2013:1-38.
[2] ALVES M K,ROSSI R.An extension of the partition of unity finite element method[J].JournaloftheBrazilianSocietyofMechanicalSciencesandEngineering,2005,27(3):209-216.
[3] BELYTSCHKO T,GRACIE R,VENTURA G.A review of extended/generalized finite element methods for material modeling[J/OL].ModellingandSimulationinMaterialsScienceandEngineering,2009,17(4):043001.doi:10.1088/0965-0393/17/4/043001.[2017-05-12] http://iopscience.iop.org/article/10.1088/0965-0393/17/4/043001/meta.
[4] BELYTSCHKO T,MOЁS N,USUI S,et al.Arbitrary discontinuities in finite elements[J].InternationalJournalforNumericalMethodsinEngineering,2001,50(4):993-1013.
[5] MOЁS N,GRAVOUIL A,BELYTSCHKO T.Non-planar 3D crack growth by the extended finite element and level sets-Part I:Mechanical model[J].InternationalJournalforNumericalMethodsinEngineering,2002,53(11):2549-2568.
[6] ABDELAZIZ Y,HAMOUINE A.A survey of the extended finite element[J].Computers&Structures,2008,86(11):1141-1151.
[7] CHESSA J,WANG Hongwu,BELYTSCHKO T.On the construction of blending elements for local partition of unity enriched finite elements[J/OL].InternationalJournalforNumericalMethodsinEngineering,2003,57(7):1015-1038.http://onlinelibrary.wiley.com/doi/10.1002/nme.777/full.
[8] SUKUMAR N,CHOPP D L,MOЁS N,et al.Modeling holes and inclusions by level sets in the extended finite element method[J].ComputerMethodsinAppliedMechanicsandEngineering,2001,190(46):6183-6200.
[9] FRIES T P.A corrected XFEM approximation without problems in blending elements[J/OL].InternationalJournalforNumericalMethodsinEngineering,2008,75(5):503-532.http://onlinelibrary.wiley.com/doi/10.1002/nme.2259/full.
[10] ARNOLD D N.An interior penalty finite element method with discontinuous elements[J].SIAMJournalonNumericalAnalysis,1982,19(4):742-760.
[11] GRACIE R,WANG Hongwu,BELYTSCHKO T.Blending in the extended finite element method by discontinuous Galerkin and assumed strain methods[J/OL].InternationalJournalforNumericalMethodsinEngineering,2008,74(11):1645-1669.http://onlinelibrary.wiley.com/doi/10.1002/nme.2217/full.
[12] Sanford R J.Principles of Fracture Mechanics[J].Upper Saddle River Nj,2002,12:29-44.
[13] 中交规划设计研究院有限公司.公路钢结构桥梁设计规范:JTG D64—2015[S].北京:人民交通出版社股份有限公司,2015.
CCCC Highway Consultants CO.,Ltd.SpecificationforDesignofHighwaySteelBridge:JTGD64-2015[S].Beijing:China Communications Press Co.,Ltd,2015.
[14] 曾勇,渠昱,谭红梅,等.大跨悬索桥主缆-吊杆-钢箱梁一体模型疲劳试验研究[J].四川大学学报(工程科学版),2016,48(4):78-84.
ZENG Yong,QU Yu,TAN Hongmei,et al.Fatigue experimental study on integration model including main cable,hangers and box main girder of long-span suspension bridge[J].JournalofSichuanUniversity:EngineeringScienceEdition,2016,48(4):78-84.
[15] The American Association of State Highway and Transportation Officials(AASHTO).LRFDBridgeDesignSpecifications[S].4thEd.Washington,D C:AASHTO,2007.
[16] CHOWDHURY P,SEHITOGLU H.Mechanisms of fatigue crack growth-a critical digest of theoretical developments[J].Fatigue&FractureofEngineeringMaterials&Structures,2016,39(6):652-674.
[17] EL-HADDAD M H,TOPPER T H,SMITH K N.Prediction of non-propagating cracks[J].EngineeringFractureMechanics,1979,11(3):573-584.
[18] 刘艳萍,陈传尧,李建兵,等.14MnNbq焊接桥梁钢的疲劳裂纹扩展行为研究[J].工程力学,2008,25(4):209-213.
LIU Yanping,CHEN Chuanyao,LI Jianbing,et al.Fatigue crack growth behavior for the weld heat-affected zone of 14MnNBQ bridge steel[J].EngineeringMechanics,2008,25(4):209-213.
[19] NIEMI E,FRICKE W,MADDOX S J,et al.FatigueAnalysisofWeldedComponents——Designer’sGuidetotheStructuralHot-SpotStressApproach:IIW-1430-00[S].Cambridge:Woodhead Publishing Limited,2006.
[20] 李传习,李游,陈卓异,等.钢箱梁横隔板疲劳开裂原因及补强细节研究[J].中国公路学报,2017,30(3):121-131.
LI Chuanxi,LI You,CHEN Zhuoyi,et al.Fatigue cracking reason and detail dimension of reinforcement about transverse diaphragm of steel box bridge[J].ChinaJournalofHighwayandTransport,2017,30(3):121-131.
