某异形景观桥人致振动荷载取值及舒适度分析
2018-04-13张雪松陈永辉王继祥
张雪松,陈永辉,王继祥
(重庆交通大学 土木工程学院,重庆 400074)
桥梁结构振动,是伴随着外作用输入(车辆动荷载、人群动荷载、风力、地震波),结构体系变形能量和运动能量相互转换的周期性过程。汽车荷载通过冲击力系数达到了对车辆静荷载的放大作用,而冲击系数由结构固有频率决定。随着新型材料与施工工艺的使用,桥梁结构不断向着大跨、悬挑等更轻柔、阻尼更小的方向发展。对于以人群荷载为主的人行桥,其动力特性较复杂,在人行荷载作用下,会发生一定程度的振动,使人产生不舒适感。通过建立动力学数学模型,采用时域法或频域法分析人体不同部位对外界振动的响应[1]。故如何使桥体在保证强度、刚度和稳定性的同时满足舒适度要求已成为结构设计的重点、难点。
结构振动舒适度评价标准主要分为两类:计算桥体振动特性,为防止人与人行桥共振,减少行人不舒适感,避免发生危险事故,要求天桥上部结构竖向自振频率不应小于3 Hz[2];分析外部荷载激励下的振动响应,采用傅立叶级数来表示人行荷载激励[3]。
1 工程概况
1.1 工程概况及结构参数
拟建工程为悬挑式景观玻璃桥(图1),平台布置于场地陡崖边缘向外悬挑长度达70 m,采用46根拉索将桥塔与玻璃平台连接成为空间异形结构,作为旅游观光设施极具视觉冲击力。该工程为国内最大跨度悬挑景观桥,其结构自振频率较低,特殊的结构形式决定了在人行荷载激励下极易发生共振和行走舒适度较差等问题。玻璃桥主要结构为钢管、钢箱梁、铝合金挑梁、玻璃,主要结构参数见表1。

图1 成桥效果Fig. 1 Bridge effect diagram
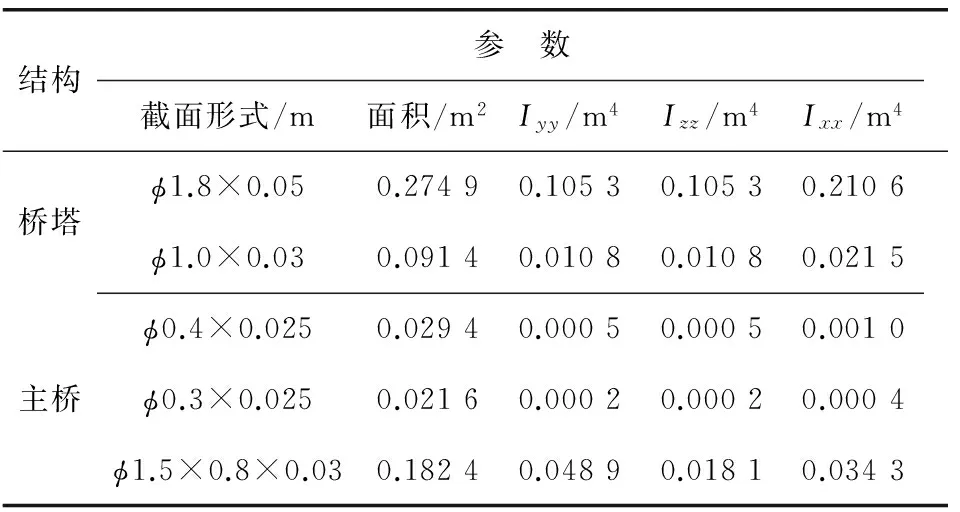
表1 主要结构参数Table 1 Main configuration parameters
1.2 桥体振动特性
新型材料及异形结构形式易引起人群舒适度较差等问题。故需要对景观桥进行人致振动分析,并评估其舒适度级别,并依此提出相应的减震措施。初步设计阶段通过改变截面或结构形式以提高全桥整体、局部刚度,从而减少活载变形、增大自振基频。从活载挠度、动力特性两个方面对比以下结构形式:
1) 原结构(主桥部分钢管采用φ0.4×0.025);
2) 主桥所有钢管均采用φ0.4×0.025;
3) 在原结构形式上,拉索直径修改为7.5 cm;
4) 所有钢管采用φ0.4×0.025,拉索直径为7.5 cm;
5) 优化后结构(在原结构主桥顶面、底面做平联)如图2,其交叉线条即为平联结构。

图2 优化后主桥效果Fig. 2 Main bridge effect diagram after optimization
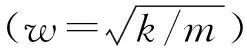
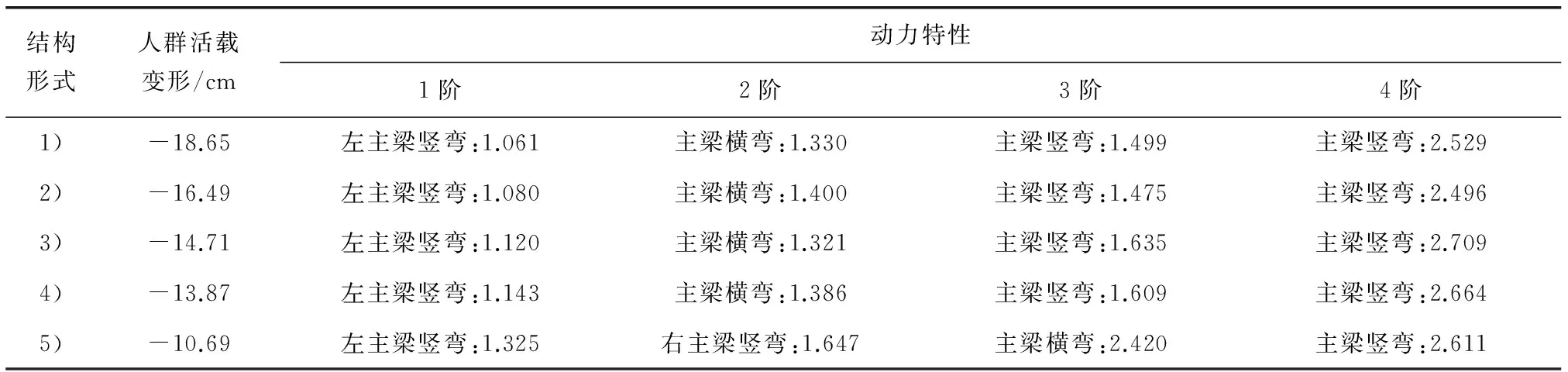
表2 不同方案结构响应汇总Table 2 Summary of structure response of different programs
笔者通过对主桥结构形式优化:顶、底面增加平联杆件使其成为“封闭箱梁”形式,增大全桥抗扭刚度,玻璃桥自振频率增幅明显,活载变形大大减小。但全桥竖向自振频率仍小于3 Hz,无法满足要求;若仍采用竖向结构基频控制大跨人行桥设计则显得较为严格。同时研究表明:在一定情况下,即使结构基频落入人群振动敏感区时,也可满足人群舒适度要求[4]。在结构响应中:振动位移、速度和加速度这3要素,加速度对人生理和心理感受影响最大,直接决定了人行走舒适度,因而建议采用振动响应加速度进行舒适度评价。加速度参数在实际工程中有广泛应用,如桥梁基础冲孔桩施工中引进地表振动加速度,以分析冲击能对振动速度的影响[5]。
人行荷载作为一种动力荷载,是人行桥振动最主要的激励来源,步行荷载动力特性是影响结构振动分析精度与振动控制效果最主要的因素。由于行人具有自主性,其在桥面上分布具有随机性,故人行荷载模拟是当前世界范围内人行桥研究的难点。国外学者已对人群荷载取值做了相应要求,由于国内人群身高、体重等特征参数与西方国家人群有较大差异,直接采用国外人群荷载取值必将引起较大误差。因此,以国人体质为基础,建立和研究人群荷载模型,具有必要性和迫切性。
2 步行力产生原理及特点
2.1 步行力产生原理
步行,按照生物力学观点就是人体在行进过程中,全身肌肉都同时参与工作。步行者在行走过程中,身体重心沿复杂的螺旋形曲线向前运动。行走时左、右两足跟之间的向距离称为步长,横向距离称为横距。于国内人群而言,成年男性每复步一般为150~160 cm[6]。
行进过程中,人体重心上下、左右摆动,产生竖向周期性荷载激励,荷载频率等同于步行荷载频率。在双腿交替行进过程中,人体重心会发生“Z”字形左右摆动,产生水平侧向动力荷载,其频率为步频的一半。任一时刻行人对景观桥的动力荷载不同,从而产生一个动态的时程力,包括竖向时程力、纵向时程力、横向时程力。由于竖向时程力对结构影响最大,笔者以该方向时程力进行分析,其余方向时程力类比于竖向时程力。
笔者将人群荷载分解为3个方向分量形式,各方向时程曲线如图3。其中:图3(a)为竖向力时程;图3(b)为横向力时程;图3(c)为纵向力时程[7]。由图3(a)可看出:竖向力时程具有两个波峰和一个波谷;在人类行进过程中,需双腿交替运动,两下肢交替运动,带动整个身体前进。

图3 单步力3方向分量的时程Fig. 3 Time history of the three direction component of a single step force
2.2 步行力特点
人行荷载不同于其他可变荷载,具有以下特点[8-9]。
2.2.1显著的周期性
人行荷载具有明显的周期性,成年人正常行走时的步频在1.6~2.4 Hz,竖向力前3阶谐波都可能激发桥梁振动;横向力步行力频率在3.2~4.8 Hz,横向力则一般只考虑1阶谐波作用。
2.2.2窄带随机过程
由于行人荷载的特殊性,其步长、频率变化程度没有其他可变荷载(如汽车荷载、地震荷载等)剧烈,步行步长、频率均是在很窄范围内随机分布。当桥上行人较多时,随着基数增大,必将导致初相位相等的人越来越多,若此时这群人的脚步频率与桥梁结构自振频率接近甚至相同时,桥梁就会产生明显振动,进而影响行人舒适度甚至结构破坏。
2.2.3人桥“互动”
行人即是结构的激振源,又是感受体。若人行桥发生振动,将严重地影响到行人的步行舒适性及安全性,部分行人会停下来依靠桥上栏杆来保持平衡,更多人群会通过调整自己步频、步长等方式来适应桥梁振动和改善自己行走舒适度,这种现象称为“集体同步”现象[10-11],这种行为反而会加剧桥梁横向振动。
3 人行荷载模型
作为人行桥振动的主要激励来源,人行荷载对人行桥振动机理研究起着至关重要作用,必须建立合理的行人脚步荷载数学模型,F.C.HARPER等[12-13]采用测力板对人行荷载测量做了研究。目前学界建立的单人脚步荷载时域数学模型有两类:确定性模型和随机性模型。确定性荷载模型相对简单,国外在人行桥动力设计中普遍采用确定性模型对结构进行评估。
3.1 单人荷载模型
人行荷载具有显著周期性,其竖向力和侧向力都可用无穷级数(傅里叶级数)的形式表达出来[14]。
竖向步行力模型如式(1):
(1)
侧向步行力模型如式(2):
(2)
式中:t为时间;W为体重;fp为步行荷载频率;αvi为第i阶竖向力动载因子;αli为第i阶侧向力动载因子;φvi为第i阶竖向力谐波相位角;φli为第i阶侧向力谐波相位角。
表3罗列了各国学者提出或经试验测得的各阶谐波动载因子。

表3 不同学者提出的单人动载因子(DLF)Table 3 Dynamic load factor(DLF) proposed by different scholars
由表3可知:竖向1阶谐波动载因子最大,对结构振动贡献最大,高阶谐波动载因子迅速减小,在满足工程要求前提下只需考虑前3阶或前4阶动载因子引起的激励荷载。
3.2 多人荷载模型
多人荷载模型相对于单人荷载模型更为复杂,随着桥上人数增多,其行走过程的随机性也逐渐增大。由于人群初相位不同,动力荷载并不能简单等同于单人动力荷载乘桥上人群总数,而要小于该值。因此不能直接使用单人荷载动载因子,依据表4不同人群密度,人群荷载动载因子α*也有区别。

表4 多人荷载类型划分Table 4 Partition of multi-person load type
3.2.1小组结伴而行
竖向脚步动荷载的一阶谐波分量很容易实现同步,假定小组人群行走完全同步,但2阶、3阶谐波引起同步的可能性很小,简化计算时其效应可忽略。人群荷载模型的动载因子与单人荷载的动载因子相同,即α*=α,小组行人步行力模型可用式(3)所采用的单人荷载模型乘以小组人数来计算。
Fp=W·α·sin(2πfp·t)·n
(3)
3.2.2低密度人群自由行走
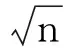
(4)
3.2.3高密度人群流动
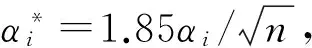
(5)
4 景观玻璃桥人致振动舒适度分析
玻璃桥采用自振频率控制设计是不现实的。故笔者采用动力响应评价方法,利用结构在人行荷载激励下的峰值加速度来对其进行舒适度评价。
动力设计基本过程为[15]:依据结构动力特性,确定敏感频率范围;人致振动响应分析,以外界激励荷载引起结构最大加速度评估舒适性级别,舒适性级别见表5。

表5 人行桥的加速度舒适性判定标准Table 5 Judging criteria of the acceleration comfort of a footbridge
4.1 人群荷载模拟
时程分析法可准确确定在外界荷载激励下结构内力、位移加速度等响应随时间的反应,其缺点主要是对计算机配置要求高,计算周期长。时程分析加载形式有固定点加载法、移动加载法,初步设计阶段采用固定荷载法计算人群激励下的最大响应。依据人群活载影响面(线)数据、振型模态,采用等效原则将压力荷载转换为节点荷载固定施加在引起最大加速度的点上。
本桥相邻两阶振型的自振频率比较接近,且前4阶模态均位于活载敏感频率范围,故激励荷载分别采用1.50、1.75、2.00、2.25、2.50、2.75、3.00、3.25、3.50 Hz,以期进行扫频分析,行人质量取为75 kg,人群密度取1人/m2。选取具有代表性的3个节点:节点1330(主桥右侧)、节点1331(主桥左侧)和节点1941(主桥最前端)进行分析,分别对比不同频率激励荷载作用下各点的竖向加速度值,如图4。
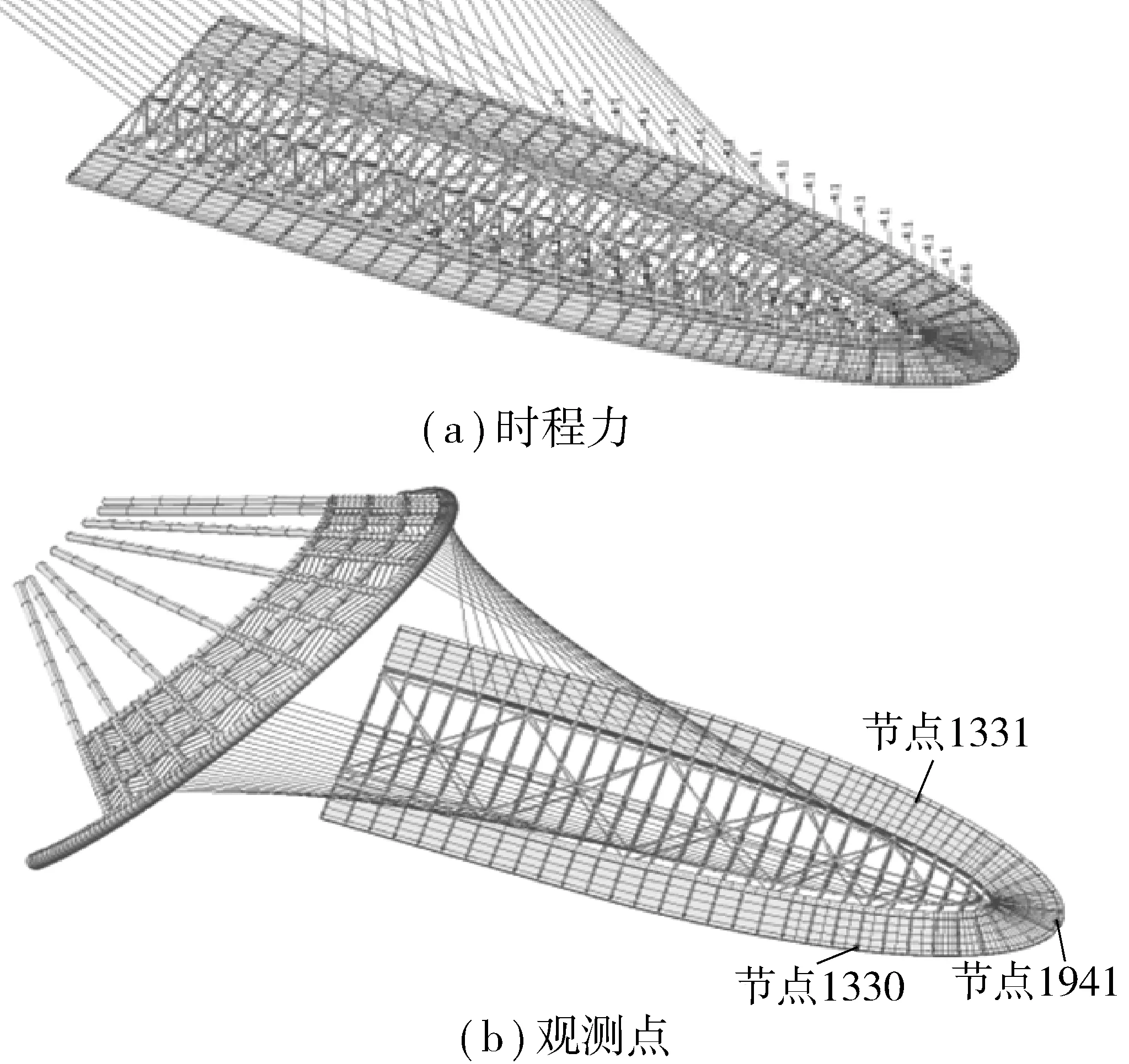
图4 时程力加载及观测点Fig. 4 Diagram of time history force loading and observation points
根据对人行荷载描述,该景观玻璃桥考虑不利工况为:高密度人群流动。
玻璃桥面宽取用3.8 m,相邻挑梁间距2.4 m,故面积为3.8×2.4=9.12 m2,相邻挑梁之间桥上近似为9人。根据表6不同频率各阶动载因子,得出式(6)的等效节点力。
(6)

表6 不同荷载频率的动载因子Table 6 Dynamic load factor of different load frequency
4.2 动力时程分析
人群激励荷载频率为1.5 Hz,人行荷载激励下选取1330、1331、1941这3个节点的竖向加速度时程,如图5。
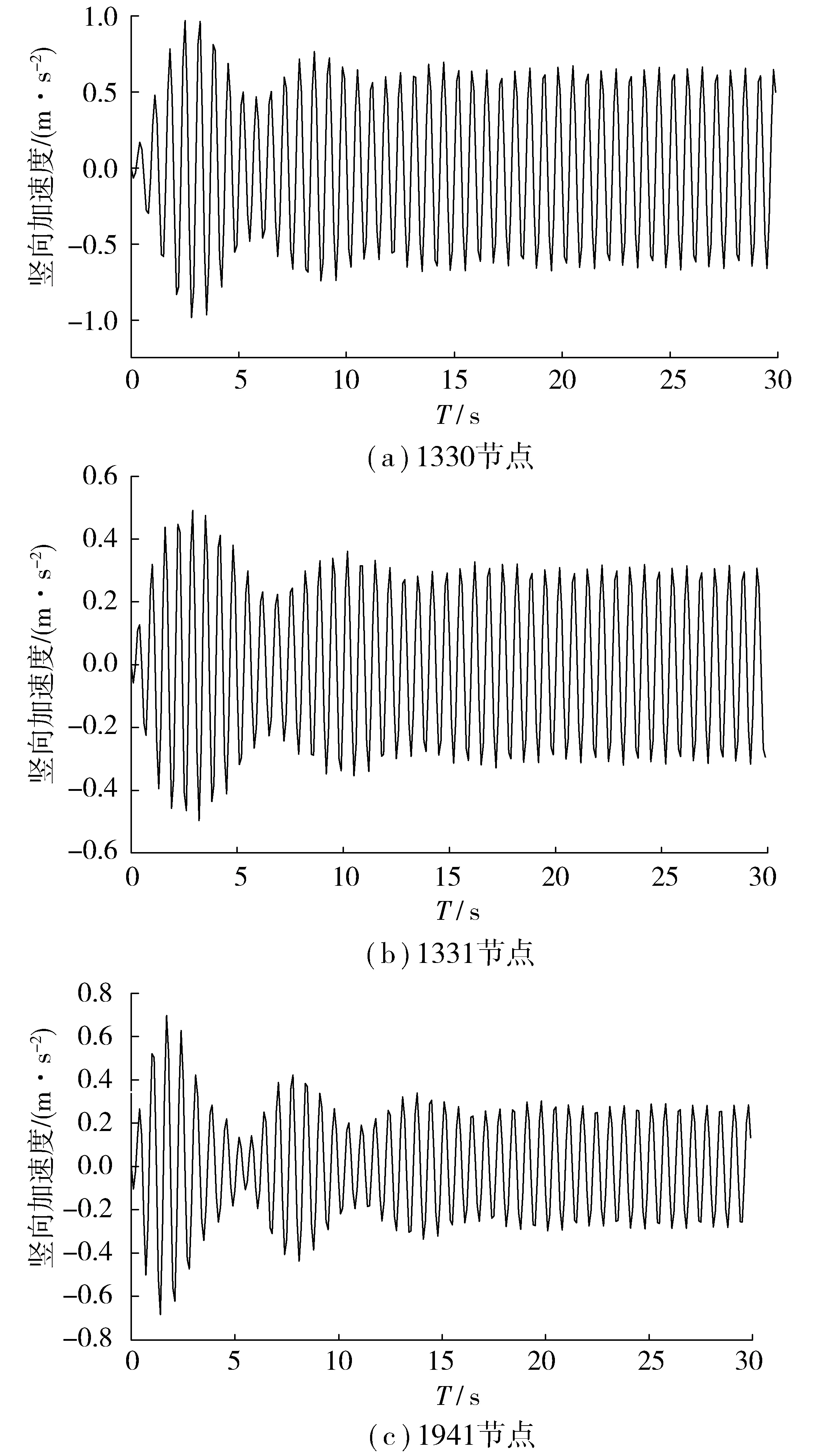
图5 节点加速度时程Fig. 5 Time history of node acceleration
限于篇幅,笔者不再一一列出其余荷载激励,对各点在不同频率下,加速度峰值进行扫频分析,具体结果见图6。

图6 观测点加速度峰值扫频分析结果Fig. 6 Sweep-frequency analysis results of acceleration peak values of observation points
5 结论及展望
使用傅立叶三角级数将脚步力等效为外界激励加载到结构上进行时程计算,对观测点进行加速度扫描分析,有如下结论:
1) 当增加截面尺寸不能显著改善结构动力响应时,通过优化部分结构形式可使得活载挠度、自振基频达到预想结果;
2) 控制结构竖向基频不应小于3 Hz过于严格,必将引起资源浪费。参阅相关文献,采用各阶动载因子参数,将脚步力荷载等效为各阶正弦函数代数和的形式。对结构进行动力响应分析,以加速度控制人群舒适度级别;
3) 基于振型模态、活载影响面(线)确定固定荷载加载点,初步设计阶段,采用定点加载法比移动荷载法效率更高,且当结构频率较低时,固定荷载法的结果相对更保守;
4) 由加速度峰值扫描分析结果,验证了外界激励等于或接近结构竖向基频时,振动幅度最大,极易发生共振;
5) 加速度峰值较大时,易引起人群不舒适感,严重时会导致桥梁毁坏,建议加装TMD阻尼器。
参考文献(References):
[1]钱凯,胡启国,李力克.基于人-车-路耦合振动系统的儿童乘坐舒适性[J].重庆交通大学学报(自然科学版),2013,32(2):351-359.
QIAN Kai,HU Qiguo,LI Like.Children ride comfort based on human-vehicle-road coupled system of vibration[J].JournalofChongqingJiaotongUniversity(NaturalScience),2013,32(2):351-359.
[2]北京市市政工程研究院.城市人行天桥与人行地道技术规范:CJJ 89—95[S].北京:中国建筑工业出版社,1996.
Beijing Municipal Engineering Research Institute.TechnicalSpecificationofUrbanPedestrianOvercrossingandUnderpass:CJJ89—95[S].Beijing:China Architecture & Building Press,1996.
[3]BACHMANN H,PRETLOVE A J,RAINER H.DynamicForcesfromRhythmicalHumanBodyMotions[M].Basel:Birkhause Verlag,1995.
[4]孙沪.异形钢拱人行桥通行舒适度及其控制研究[D].杭州:浙江工业大学,2015.
SUN Hu.TheResearchonTrafficComfortIndexandVibrationComfortControlofSpecial-shapedSteelArchFootbridge[D].Hangzhou:Zhejiang University of Technology,2015.
[5]佘艳华,苏华友,肖正学,等.桥梁桩基冲孔桩施工的微振动响应研究[J].重庆交通大学学报(自然科学版),2011,30(1):35-38.
SHE Yanhua,SU Huayou,XIAO Zhengxue,et al.Study on the vibration response to punched pile construction of bridge pile foundation[J].JournalofChongqingJiaotongUniversity(NaturalScience),2011,30(1):35-38.
[6]钱竞光,宋雅伟,叶强,等.步行动作的生物力学原理及其步态分析[J].南京体育学院学报(自然科学版),2006,5(4):1-7.
QIAN Jingguang,SONG Yawei,YE Qiang,et al.The biomechanics principle of walking and analysis on gaits[J].JournalofNanjingInstituteofPhysicalEducation(NaturalScience),2006,5(4):1-7.
[7]袁旭斌.人行桥人致振动特性研究[D].上海:同济大学,2006.
YUAN Xubin.ResearchonPedestrian-InducedVibrationofFootbridge[D].Shanghai:Tongji University,2006.
[8]刘军进,肖从真,潘宠平,等.跳跃和行走激励下的楼盖竖向振动反应分析[J].建筑结构,2008,38(11):108-110.
LIU Junjin,XIAO Congzhen,PAN Chongping,et al.Investigation on response of floor vibration under jumping and walking excitation[J].BuildingStructure,2008,38(11):108-110.
[9]陈政清.人行桥的振动与动力设计[M].北京:人民交通出版社,2009.
CHEN Zhengqing.VibrationandDynamicDesignofPedestrianBridge[M].Beijing:China Communications Press,2009.
[10]DALLARD P,FITZPATRICK A,FLINT A,et al.The London MillenniumFootbridge[J].StructuralEngineer,2001,79(171):17-33.
[11]DALLARD P,FITZPATRICK A,FLINT A,et al.London Millennium Bridge:pedestrian-induced lateral vibration[J].JournalofBridgeEngineering,2001,6(6):412-417.
[12]HARPER F C.The mechanics of walking[J].ResearchAppliedinIndustry,1962,15(1):23-28.
[13]HARPER F C,WARLOW W J,CLARKE B L.The force applied to the floor by the foot in walking[J].NationalBuildingStudies,1961,12(1):32-38.
[14]PAVIC A,REYNOLDS P.Vibration serviceability of long-span concrete building floors,part1:review of background information[J].Shock&VibrationDigest,2002,34(3):191-211.
[15]HIVOS S.GuideLineforDesignforFootbridge[R].U.S.A.:HIVOSS,2007:1-33.
