考虑延误与通行能力的交叉口信号周期优化
2018-04-13张立立张海波修伟杰李正熙
王 力,张立立,李 敏,张海波,修伟杰,李正熙
(北方工业大学 城市道路交通智能控制技术北京重点实验室,北京 100144)
目前,城市道路交叉口信号控制仍以定时控制和感应控制为主。由于受检测设备完好性的制约以及感应控制策略不适用于过饱和交通流控制的影响,定时控制成为大多数城市交通信号控制首选方法。
控制参数优化设计是定时控制的核心部分。杨锦冬等[1]以延误最小、排队车辆数最少为目标,采用YD算法求解最优信号周期;王秋平等[2]建立了以平均延误时间最短、平均停车次数最少为目标的单点交叉口信号配时优化非线性函数模型,并采用遗传算法及遗传模拟退火算法对其进行求解;沈峰等[3]和高云峰等[4]分别将延误时间、排队长度、行程时间等指标组成多目标控制,采用NSGA II(none-dominated sorted genetic algorithm II)算法进行优化;臧利林等[5]以车辆平均延误为优化目标,采用模糊逻辑进行交叉口信号控制策略设计;张本等[6]和刘权富等[7]分别将通行能力与车辆尾气排放相结合,利用遗传算法实现交叉口多目标优化;陈小红等[8]考虑了道路使用率、出行者时间效率以及环境效益之间的协调关系,并结合多目标规划模型,以通行能力最大、停车率及平均延最小为目标,建立交叉口信号配时多目标优化模型;郭旭明等[9]定义了交叉口旅行时间可靠性,并采用遗传算法进行优化。唐国磊等[10]通过建立微观交通仿真模型分析大车混入时饱和流率值和相位损失时间的变化规律,进而推求疏港道路信号控制交叉口通行能力。陈兆盟等[11]利用车头时距的方差和时间占有率作为判别参数结合周期内排队车辆的消散,出了一种结合信号控制优化的交通状态及其真实性的判别方法。
以上研究多是从评价指标(延误、停车次数、车辆排队等)或通行能力方面入手对交叉口信号控制参数进行优化,然而对交叉口信号控制分析研究应从通行能力和评价指标两方面入手,两者并重。基于此,笔者立足于单交叉口信号控制,通过分析信号周期影响下相位延误和相位通行能力梯度变化,采用相近函数为目标函数实现对信号周期的优化,能够使得周期更加适合交叉口的信号控制。
1 相位延误与通行能力关系分析
相位延误是交叉口信号控制中重要的评价指标,通过对相位延误分析可获知车辆通过交叉口时的受阻滞情况和信号控制效果。车辆在通过交叉口时产生的延误,主要取决于车辆到达率和交叉口通行能力。相位通行能力是表征相位供需的主要参数,通过相位通行能力可获知信号控制满足交通需求程度。对交叉口信号控制分析研究可从相位延误和相位通行能力之间的关系入手。
笔者以交叉口第K周期内的交通组成和信号控制为例,对无初始排队交叉口欠饱和、临界饱和和过饱和情况下的相位延误和相位通行能力之间关系进行分析。
1.1 单交叉口模型
为便于分析,笔者选取典型两相位控制单交叉口进行研究,交叉口相位分别为“东西直行”和“南北直行”,如图1。
其中相位定义如下:
1) 相位1:北直行和南直行的流量分别为q1,3(k)和q3,1(k);
2) 相位2:东直行和西直行的流量分别为q2,4(k)和q4,2(k);
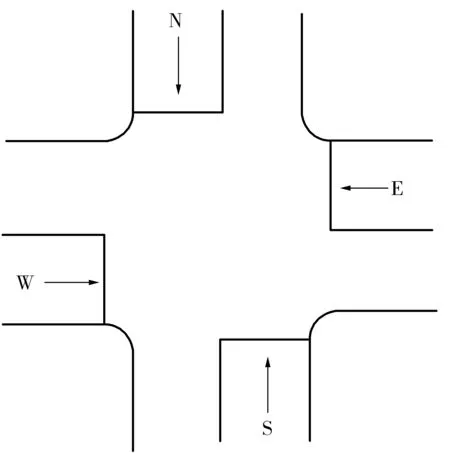
图1 交叉口相位图Fig. 1 Intersection phase
为便于简化参数分析,选择相向而行的两个行驶方向中流量较大者作为相位的关键流量qi(k),具体定义为:qi(k)=max{qi,i+2(k),qi+2,i(k)},i=1,2。
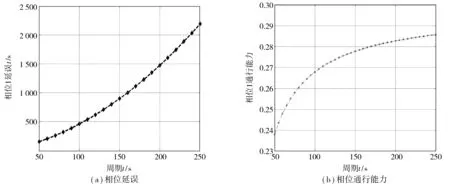
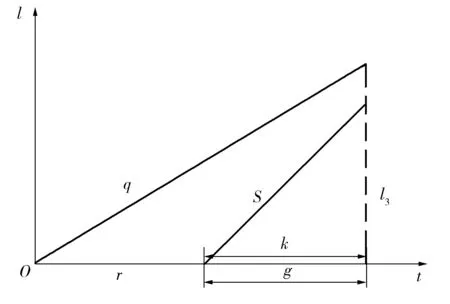
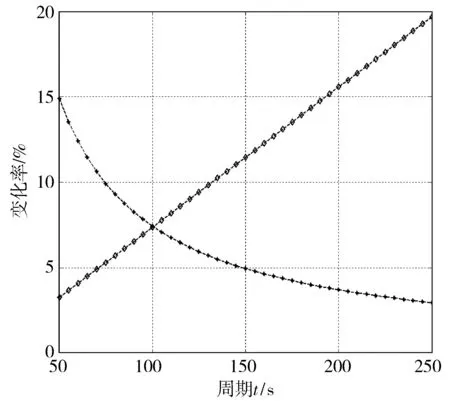
在实际交通流变化中,为避免相位关键流量qi(k)在qi,i+2(k)和qi+2,i(k)之间频繁切换,引入滞回系数h,该系数可由上游交叉口车辆放行情况确定。例如:当连续多个信号周期qi,i+2(k)+h 1.2.1欠饱和状态下相位延误与通行能力关系 欠饱和状态下相位延误与通行能力关系如图2,相位1延误如式(1): (1) 图2 欠饱和状态下排队-时间关系Fig. 2 Queuing-time graph at under saturation state 式(1)可用式(2)表述: (2) 则相位1的通行能力如式(3): (3) 由式(2)、(3)可得: (4) 在欠饱和状态下,相位延误和通行能力随周期变化如图3。相位流量[q1,q2] 一定条件下,相位1的延误和通行能力随信号周期的增大持续增加。 图3 相位延误和通行能力随周期变化Fig. 3 Phase delays and traffic capacity changing with cycle (5) 在欠饱和状态下,相位延误梯度和通行能力梯度随周期变化如图4。相位流量[q1,q2] 一定条件下,相位1延误梯度随信号周期的增大线性增大;而相位1通行能力梯度则随信号周期的增大持续减小。 图4 相位延误梯度和通行能力梯度随周期变化Fig. 4 Gradient of phase delays and gradient of traffic capacity changing with cycle 图5是相位延误梯度和通行能力梯度随周期变化。由图5可知:相位1延误梯度与通行能力梯度在信号周期变化的过程中相交于一点,这为通过梯度分析周期优化带来便利。 图5 相位延误梯度和通行能力梯度随周期变化Fig. 5 Gradient of phase delays and gradient of traffic capacity changing with cycle 1.2.2临界饱和状态下相位延误与通行能力关系 饱和状态下相位延误与通行能力关系如图6,相位1延误如式(6): (6) 由式(3)、(6)得: (7) 图6 临界饱和排队-时间关系Fig. 6 Queuing-time graph at critical saturation state 在临界饱和状态下,相位延误和通行能力随周期变化如图7。相位流量[q1,q2] 和周期一定条件下,相位1延误和通行能力为信号周期对应定值。 (8) 图7 相位延误和通行能力随周期变化Fig. 7 Phase delays and traffic capacity changing with cycle 1.2.3过饱和状态下相位延误与通行能力关系 过饱和排队与时间关系如图8。相位1延误如式(9): (9) 由式(3)、(9)得: (10) 图8 过饱和排队-时间关系Fig. 8 Queuing-time graph at over saturation state 在过饱和状态下,相位延误和通行能力随周期变化如图9。相位流量[q1,q2] 一定条件下,相位1的延误和通行能力随信号周期的增大持续增加。 (11) 在过饱和状态下,相位延误梯度和通行能力梯度随周期变化如图10。相位流量[q1,q2] 一定的条件下,相位1延误梯度随信号周期增大线性增大,而相位1通行能力梯度则随信号周期增大持续减小。 图9 相位延误和通行能力随周期变化Fig. 9 Phase delays and traffic capacity changing with cycle 图10 相位延误梯度和通行能力梯度随周期变化Fig. 10 Gradient of phase delays and gradient of traffic capacity changing with cycle 图11是相位延误梯度和通行能力梯度随周期变化。由图11可知:相位1延误梯度与通行能力梯度在信号周期变化过程中相交于一点,这与图5中显示的欠饱和状态下梯度变化趋势相同。由此可知:在各种交通状态下相位延误梯度与通行能力梯度在信号周期变化过程中都具有相同特性,基于此进行信号周期优化分析具有一定可行性。 笔者的目标是在满足信号周期最佳范围条件下,通过寻找相位延误和相位通行能力梯度变化的最短距离,得到满足相位流量需求最佳相位延误和相位通行能力组合,从而实现对信号周期的优化。 图11 相位延误梯度和通行能力梯度随周期变化Fig. 11 Gradient of phase delays and gradient of traffic capacity changing with cycle 以两相位控制单交叉口为例,其相位延误表示为:di=[d1,d2];相位通行能力表示为Ri=[R1,Ri、2]。其中:di和Ri可用式(12)、(13)表示。 (12) 约束条件为: (13) 由式(11)、(12),利用欧式距离和平方欧式距离构造函数如式(14): (14) 则有: W(d,R)= (15) 由式(15)可得目标函数,如式(16): J=minW(d,R) (16) Setp 1:利用最速梯度下降算法,分别计算相位i延误最小梯度和相位i通行能力最小梯度; Setp 2:计算arg min函数定义下的相位i延误和通行能力; Setp 3:将J=minW(d,R)设为目标函数,对函数变量进行归一化处理; Setp 4:在周期约束条件下,采用遗传算法进行优化计算。 图12 周期优化算法流程Fig. 12 Flow chart of cycle optimization algorithm 为验证文中所提算法可行性,笔者选取北京市交通学院南路和交大东路交叉口东西和南北两相位的交通数据进行仿真验证。该交叉口2个方向05:00—21:00的交通流数据如图13(每15 min采集1次,折合成小汽车当量)。 为便于与Webster算法进行对比,根据稳态理论,对上述实例交叉口建立如下基本假设: 图13 交叉口交通流量Fig. 13 Traffic flow at intersection 1) 车辆平均到达率在所取的时间段T之内稳定不变; 2) 所研究的进口断面,通行能力在相应时段内稳定不变; 3) 车辆受信号阻滞所产生的延误时间与车辆到达率的相关关系,它们在所取时段T内不变; 4) 在时间段T内,各个信号周期车辆到达率的变化是随机的,因而车辆在停车线断面受阻滞排队长度也是随机变化的。在某些信号周期内可能出现车辆的到发不平衡,产生过剩滞留车队。但经过若干周期后,过剩滞留车队将消失,即就整个时间段T而言,车辆到发始终保持平衡。 表1 信号周期优化Table 1 Signal cycle optimization 图14 流量-通行能力-延误关系Fig. 14 Flow-capacity-delay relation diagram 结合表1和图14可知:当交叉口处于欠饱和状态时,文中所提算法计算周期所产生的延误略高于Webster算法;当交叉口过饱和状态时,由于文中所有算法考虑延误和通行能力共同约束,故产生的延误要远小于Webster算法,由此知笔者所提算法计算所得信号周期能够更好的适应交通流的变化。计算所得信号周期与李峰等[14]所得结果中的最佳上限相吻合。但在交叉口处于过饱和时,由于考虑了相位延误和相位通行能力组合关系,并未考虑相位车辆排队情况,可能造成相位车辆排队增加,但由于文中重点为信号周期优化,因此将相位车辆排队影响放在后续工作中进行。 笔者从信号周期与相位延误和通行能力之间的关系入手,分析了信号周期影响下相位延误和相位通行能力随周期变化情况,进而通过分析周期影响下相位延误和相位通行能力梯度变化,利用欧式距离和平方欧式距离构建了二者的相近函数,并以此为目标函数,采用遗传算法进行求解。 通过与Webster算法计算结果进行比较,验证了文中所提算法的有效性。但笔者并未对过饱和状态下车辆排队影响进行详细分析,以及未对其他评价指标与通行能力之间的关系做详细研究,这些内容将在后续研究工作中逐步完成。 参考文献(References): [1]杨锦冬,杨东援.城市信号控制交叉口信号周期时长优化模型[J].同济大学学报(自然科学版),2001,29(7):789-794. YANG Jindong,YANG Dongyuan.Optimized signal time model in signaled intersection[J].JournalofTongjiUniversity(NaturalScience),2001,29(7):789-794. [2]王秋平,谭学龙,张生瑞.城市单点交叉口信号配时优化[J].交通运输工程学报,2006,6(2):60-64. WANG Qiuping,TAN Xuelong,ZHANG Shengrui.Signal timing optimization of urban signal-point intersection[J].JournalofTrafficandTransportationEngineering,2006,6(2):60-64. [3]沈峰,杨晓光.多目标城市道路交叉口信号配时优化算法研究[J].同济大学学报(自然科学版),2009,37(7):898-902. SHEN Feng,YANG Xiaoguang.Research on multi-object optimization algorithm of urban road traffic lights[J].JournalofTongjiUniversity(NaturalScience),2009,37(7):898-902. [4]高云峰,徐立鸿,胡华,等.交叉口定周期信号控制多目标优化方法[J].中国公路学报,2011,24(5):82-88. GAO Yunfeng,XU Lihong,HU Hua,et al.Multi-objective optimization method for fixed-time signal control at intersection[J].ChinaJournalofHighwayandTransport,2011,24(5):82-88. [5]臧利林,贾磊,林忠琴.基于模糊逻辑的交通信号控制与仿真研究[J].公路交通科技,2006,23(4):124-127. ZANG Lilin,JA Lei,LIN Zhongqin.Research of traffic signal control and simulation based on fuzzy logic[J].JournalofHighwayandTransportationResearchandDevelopment,2006,23(4):124-127. [6]张本,商蕾,高孝洪.基于遗传算法的交叉口信号配时多目标优化[J].武汉理工大学学报(交通科学与工程版),2010,34(4):845-848. ZHANG Ben,SHANG Lei,GAO Xiaohong.Traffic intersection signal-planning multi-object optimization based on genetic algorithm[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering),2010,34(4):845-848. [7]刘权富,陆百川,马庆禄,等.平面交叉口信号控制多目标优化研究[J].交通科技与经济,2014,16(1):47-50. LIU Quanfu,LU Baichuan,MA Qqinglu,et al.Traffic signal control multi-objective optimization at intersection[J].Technology&EconomyinAreasofCommunications,2014,16(1):47-50. [8]陈小红,钱大琳,石冬花.基于慢行交通的交叉口信号配时多目标优化模型[J].交通运输系统工程与信息,2011,11(2):106-111. CHEN Xiaohong,QIAN Dalin,SHI Donghua.Multi-objective optimization method of signal timing for the non-motorized transport at intersection[J].JournalofTransportationSystemsEngineeringandInformationTechnology,2011,11(2):106-111. [9]郭旭明,李瑞敏,张雄飞.基于遗传算法的交叉口信号控制可靠性优化模型研究[J].公路工程,2012,37(4):44-46. GOU Xuming,LI Ruimin,ZHANG Xiongfei.Traffic signal control reliability optimization based on genetic algorithm[J].HighwayEngineering,2012,37(4):44-46. [10]唐国磊,刘汉卿,王文渊.集装箱港区疏港道路信号控制交叉口通行能力研究[J].重庆交通大学学报(自然科学版),2016,35(4):133-136. TANG Guolei,LIU Hanqing,WANG Wenyuan.Traffic capacity of signalized intersections on collection and distribution road of container port[J].JournalofChongqingJiaotongUniversity(NaturalScience),2016,35(4):133-136. [11]陈兆盟,刘小明,吴文祥,等.结合信号控制的交通状态及其真实性判别方法[J].重庆交通大学学报(自然科学版),2016,35(6):95-100. CHEN Zhaomeng,LIU Xiaoming,WU Wenxiang,et al.Identification method of traffic state and its authenticity combined with signal control[J].JournalofChongqingJiaotongUniversity(NaturalScience),2016,35(6):95-100. [12]郝建根,侯忠生,柳向斌.基于多参数规划的单交叉口排队长度均衡控制[J].控制与决策,2013,28(4):595-599. HAO Jiangen,HOU Zhongsheng,LIU Xiangbin.Vehicle queuing length balanced-control of the signalized isolated intersection via multi-parametric programming[J].ControlandDecision,2013,28(4):595-599. [13]刘广萍,裴玉龙.信号控制下交叉口延误计算方法研究[J].中国公路学报,2005,18(1):104-108. LIU Guangping,PEI Yulong.Study of calculation method of intersection delay under signal control[J].ChinaJournalofHighwayandTransport,2005,18(1):104-108. [14]李峰,王秋平.单点信号交叉口通行能力和服务水平分析[J].城市问题,2003(2):30-33. LI Feng,WANG Qiuping.Analysis of capacity and service level of urban single signalized intersection[J].UrbanProblems,2003(2):30-33.1.2 相位延误与通行能力关系
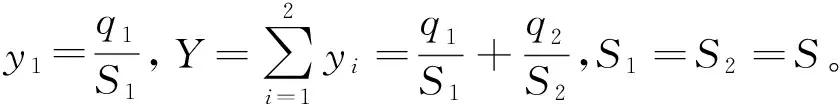

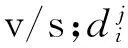
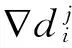
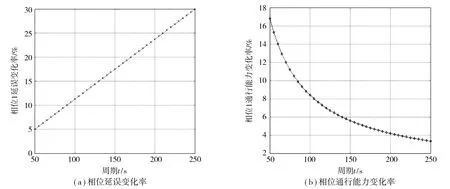

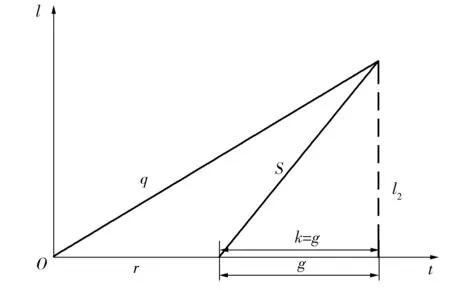
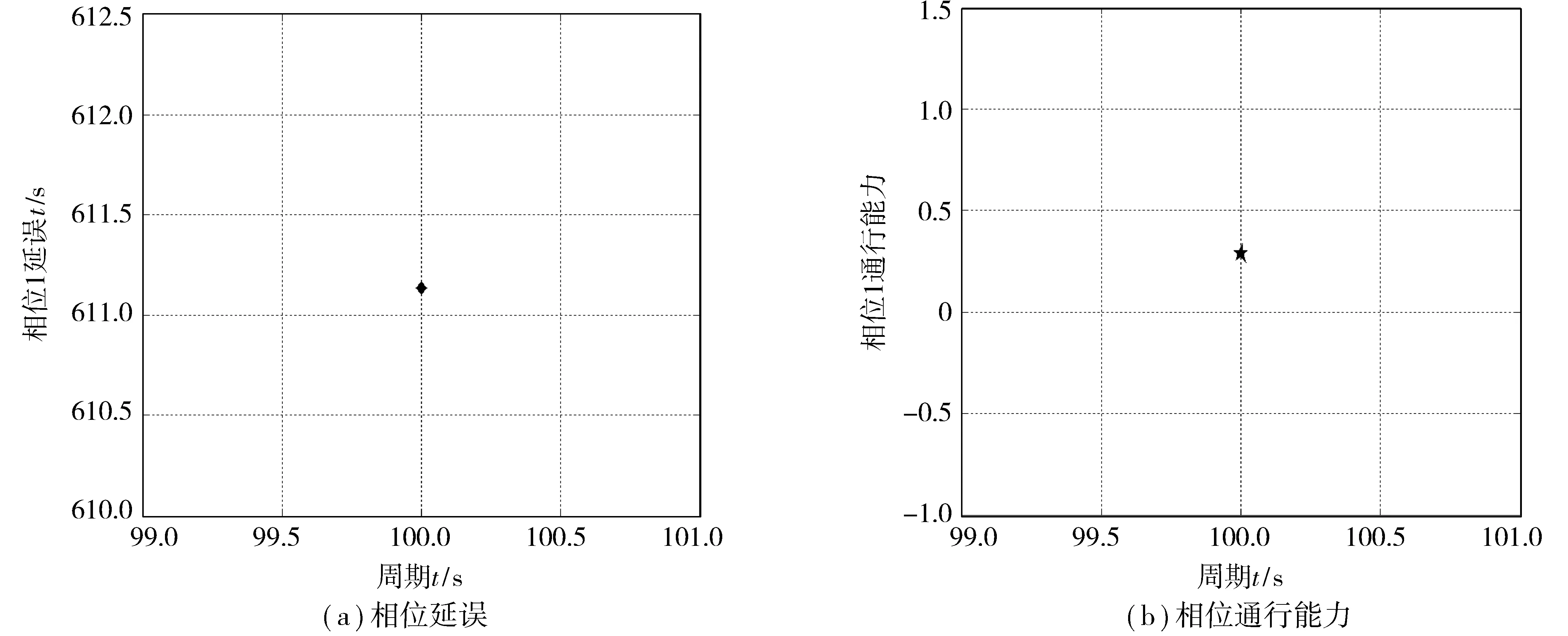


2 周期优化算法
2.1 目标函数
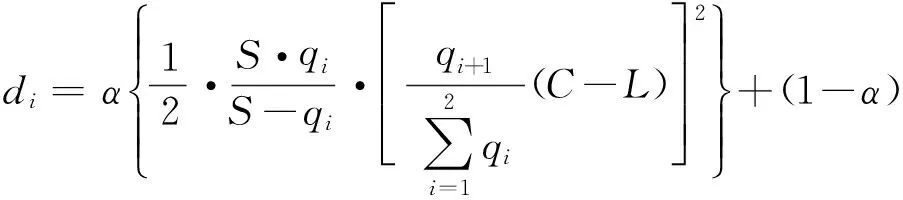
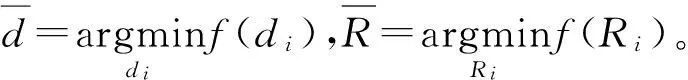
2.2 优化算法(图12)
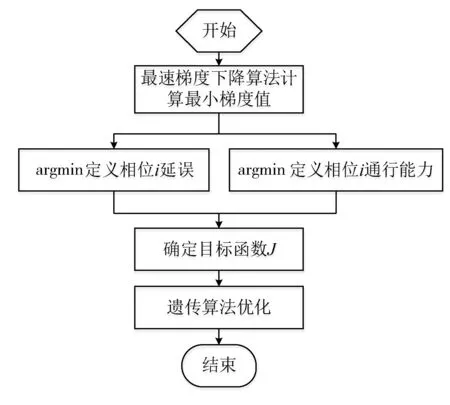
3 仿真验证
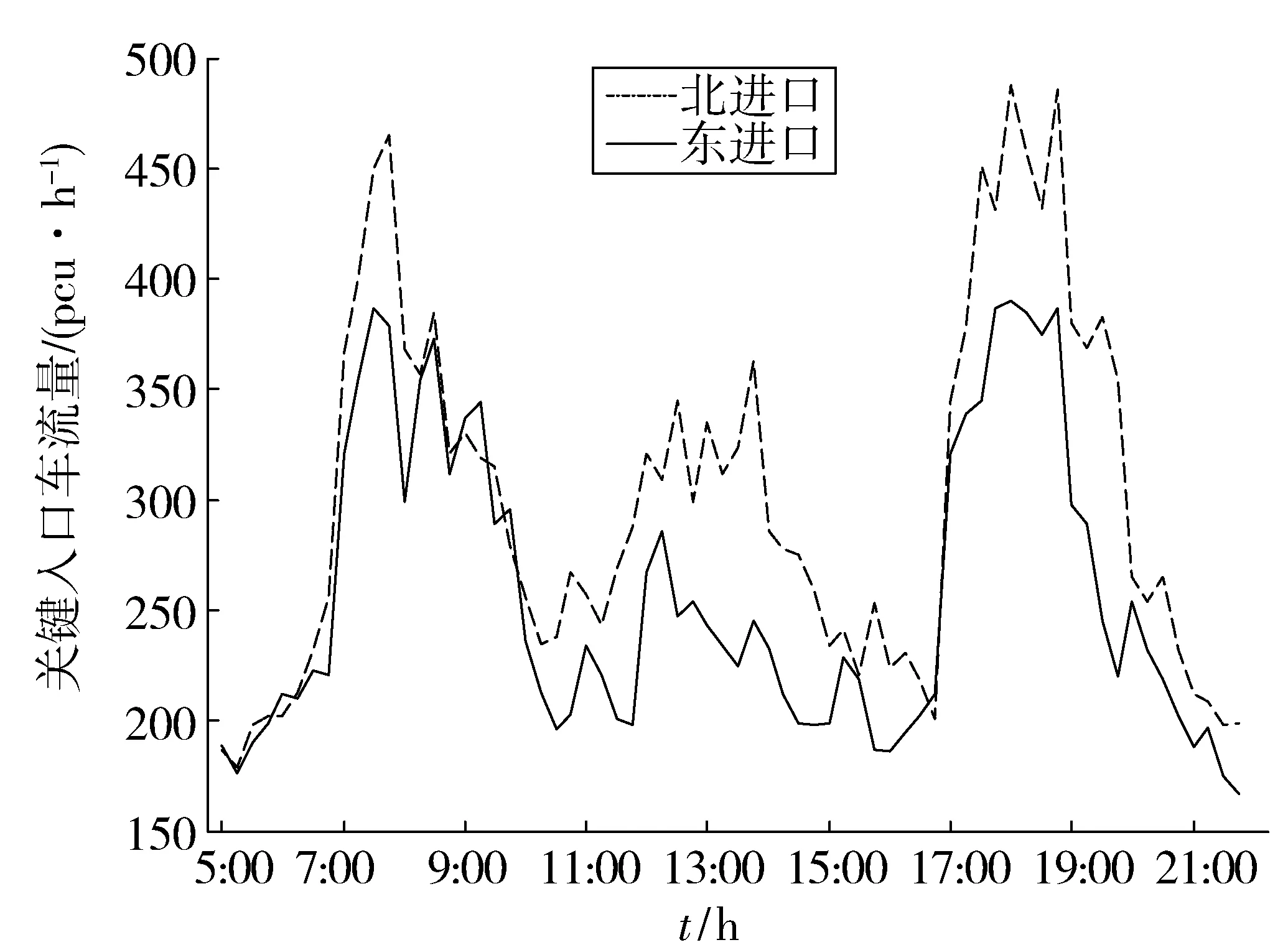

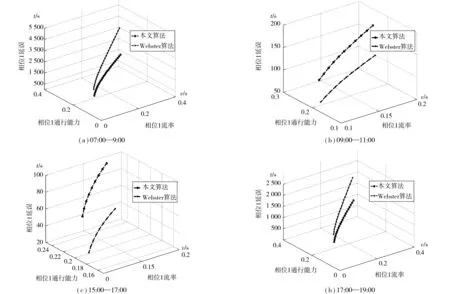
4 结 语
