地震作用下考虑土拱效应的桩间挡板土压力计算

张四平，黄亚飞，吴曙光，常　通，罗　超

(1.重庆大学 土木工程学院，重庆 400045；2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045)

0　引　言

桩板挡墙具有对桩后土体扰动小、抗滑能力大、桩位布置灵活等优点，广泛应用于建筑、交通、水利等领域中的挖(填)方工程，是一种常见的支档结构体系。桩板挡墙结构体系中，由于桩和板的刚度差异较大，对土体的约束能力不同，导致被s支护土体产生不均匀的位移。这种不均匀的相对位移使桩间土体产生了“土拱效应”[1-2]。

由于土拱效应的存在，土压力将通过拱体结构传递给相邻的桩体(即拱体的拱脚)，因此挡板只承受拱体内侧松散土体的土压力，挡板土压力大大减小[3-4]。目前桩间土拱的应用研究主要集中在桩间距和桩身受力的确定[5-10]，而关于桩间挡土构件的研究则相对较少。

在整个桩板支挡结构体系中，面积巨大的挡板占工程量的比例较大。若不考虑桩间土体的土拱效应，简单地采用传统土压力理论进行挡板结构的设计，势必造成极大的资源浪费。叶晓明[11]基于卸荷拱原理导出了柱板结构墙板上的土压力计算公式。重庆市地方标准DB 50/5029—2004《地质灾害防治工程设计规范》提出：对桩间挡板土压力采用拟化筒仓法进行计算；TB 10025—2006《铁路路基支挡结构设计规范》提出：根据桩间土的稳定状况，作用在挡板上的土压力可按全部或部分土压力计算(折减系数取0.7～0.8)。H.A.PERKO等[12]将桩间滑体简化为一个三维“筒仓”形状的楔形体，提出了一种求解桩间挡板侧向土压力的方法；梁瑶等[13]、赵晓彦等[14]假定桩间土拱形状为一等腰直角三角形，采用极限平衡法求解桩间挡板土压力。由此可见，目前对于挡板土压力的计算仍有争议。因此，基于土拱效应的挡板土压力计算理论仍需要进一步的探究。

近年来，我国地震活动趋于活跃，由于支档结构垮塌造成道路瘫痪继而影响灾区救援的悲剧时有发生。目前关于地震作用下土压力的理论研究主要集中在刚性挡土墙的领域，缺乏考虑桩间挡土拱效应影响的挡板动土压力计算研究理论。因此，无论从工程的安全性还是经济性，都需要对地震作用下桩板挡墙的土压力进行深入研究。

笔者首先对桩间土拱的几何形态做了适当的简化，然后建立了挡板土压力计算模型，尝试采用水平层分析法推导地震作用下考虑土拱效应的挡板主动土压力计算方法，并与卸荷拱法、拟化筒仓法、边坡规范算法等理论进行比较，研究挡板土压力的分布与变化情况。笔者采用控制变量来分析桩间距、土体内摩擦角、地震加速度系数等参数对挡板主动土压力的影响。

1　桩间土拱几何形态及受力特点

贾海莉等[5]认为土体自发形成土拱，必然使其最大限度地发挥效益；指出土拱的拱形及结构一定是最合理的，结构力学上称这种拱形为合理拱轴线；提出土体同时存在着直接土拱和摩擦土拱，认为土拱能否稳定存在很大程度上依赖于拱脚的承载能力。董捷[15]通过室内推桩模型实验观察到随着桩后土体推力增加，桩间土拱首先在拱脚处产生剪切破坏，这也验证了贾海莉[5]的观点。

土拱的拱形为合理拱轴线，则拱体截面的受力特点为剪力和弯矩均为0，因此土拱轴线的切向即土体单元的最大主应力方向。由于直接土拱承载能力取决于拱脚土体的剪切强度，承载能力较强；而摩擦土拱承载能力取决于拱脚与桩侧的摩阻力，承载能力较弱，所以忽略摩擦土拱效应，只考虑直接土拱效应，这样做在工程上也是偏于安全的。笔者在推导土拱的几何形态时做出如下假设：① 桩间挡板为柔性板，土拱效应可以充分发挥；② 桩后土质是均匀分布的；③ 拱后土压力是均匀分布的；④ 忽略拱体自重。则土拱问题就可以近似简化为沿桩长方向的平面应变问题。

根据“三铰拱”合理拱轴线结构力学理论，此时土拱的合理拱轴线为抛物线。笔者所在的研究团队前期通过室内推桩模型实验及小型振动台模型试验也观察到近似为抛物线形的桩间土拱形态[15-16]。因此，假定桩间土拱的形态为抛物线形，建立桩间土拱分析模型如图1，图中h为桩身横截面高度。

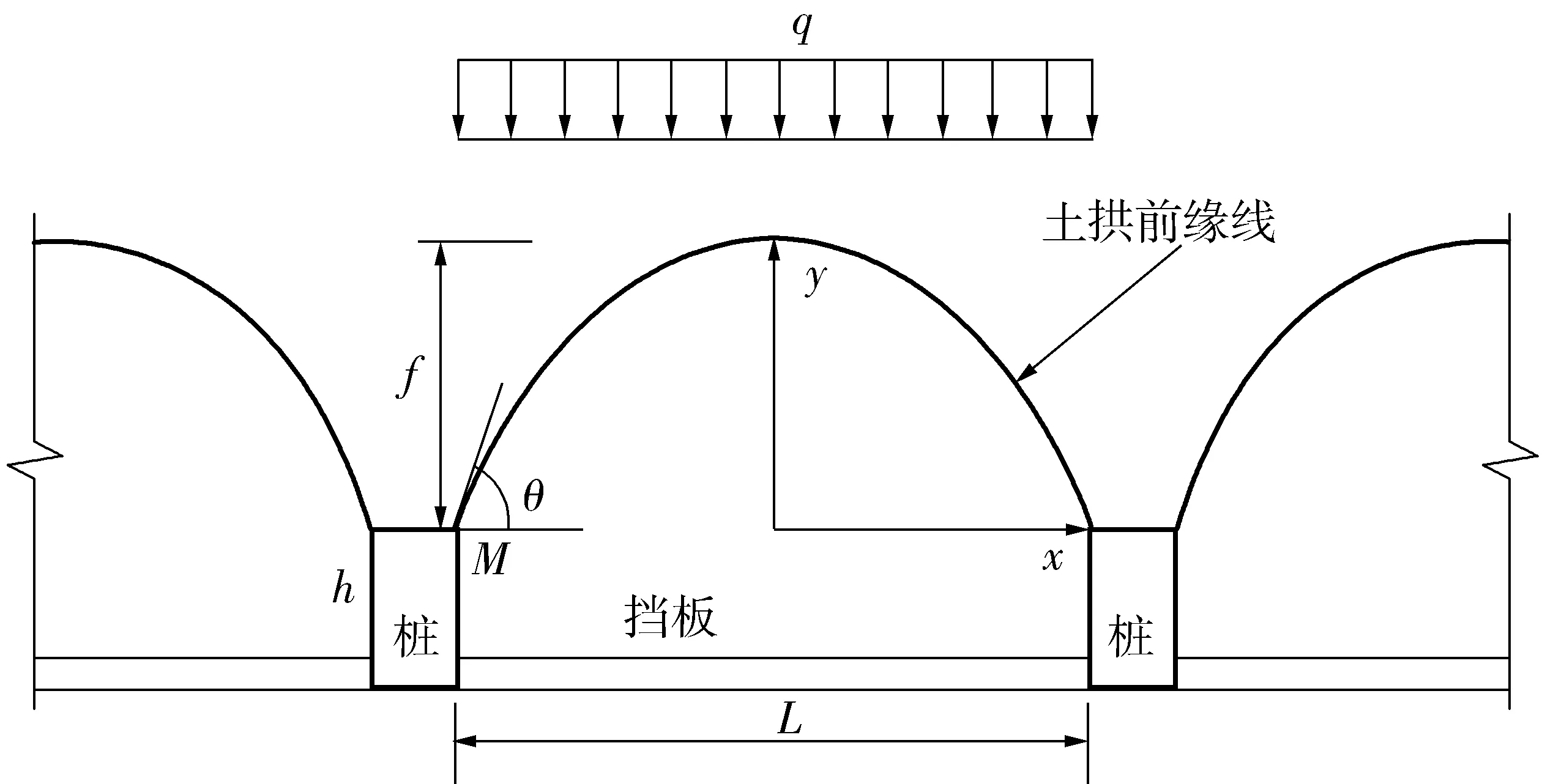
图1　桩间土拱效应分析模型Fig. 1　Analysis model of soil arching between two piles

根据设定的坐标系，可得到土拱前缘线方程

(1)

式中：f为土拱的矢高，m；L为桩间净距，m。

由于土拱前缘线是内侧屈服土体与土拱的分界线，所以M点(土拱前缘线与桩背面的交点)土体单元破裂面与x轴的夹角即抛物线的切线与x轴的夹角θ。对于M点，可认为在桩背“三角形受压区”土拱推力相互抵消〔图2(a)〕，土体与桩背面无滑移趋势。土拱的形成被认为是土体大主应力的偏转，因此有大主应力σ1垂直于桩背面，小主应力σ3平行于桩背面〔图2(b)〕。

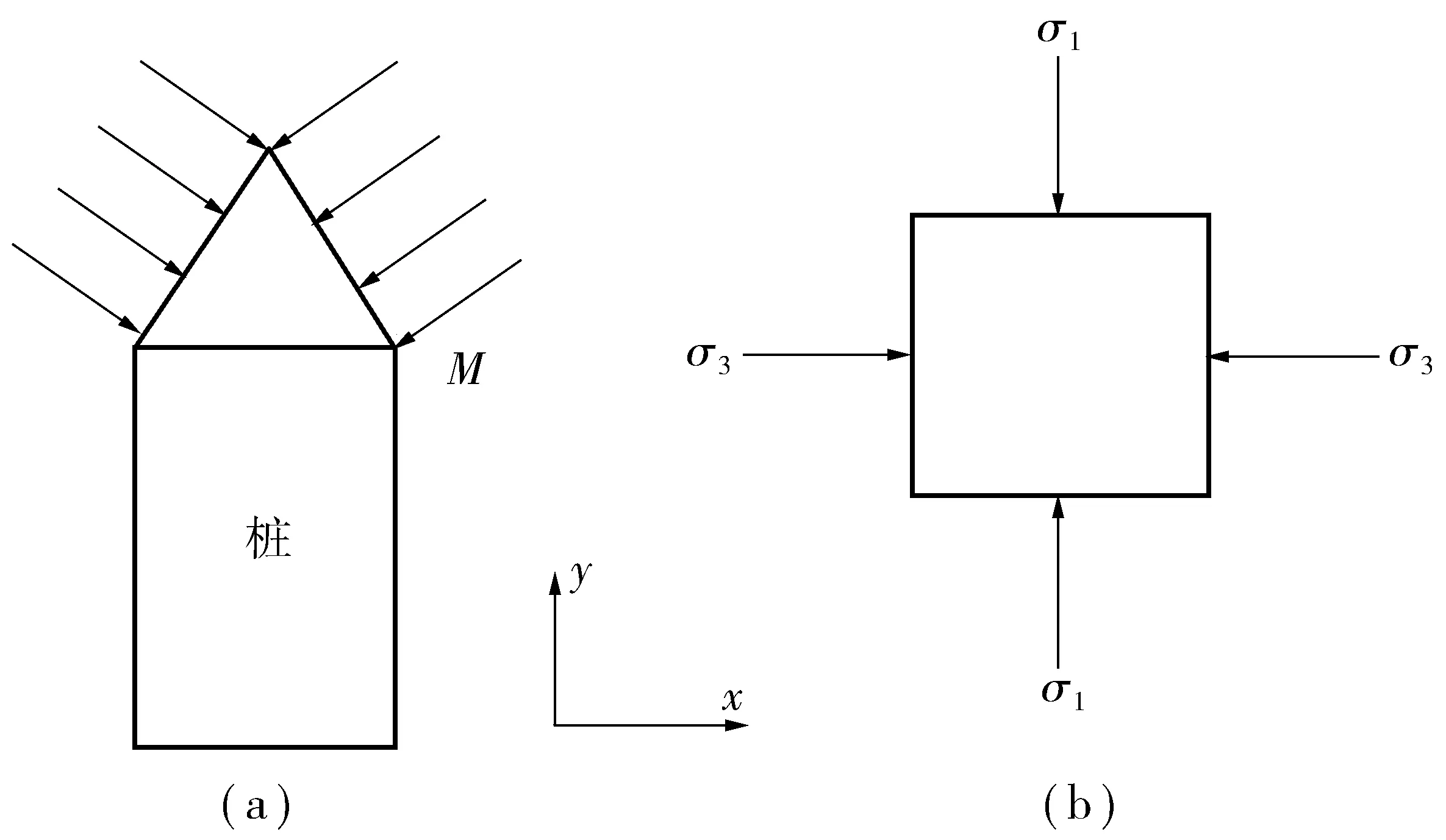
图2　桩背三角形受压区及M点的应力状态示意Fig. 2　Triangle compression zone behind pile and stress state of point M

根据Mohr-Coulomb强度理论，M点土体单元破裂面与x轴的夹角应为45°+φ/2，φ为土体内摩擦角，单位：(°)，所以θ=45°+φ/2。则有：

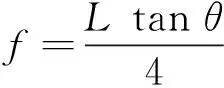
θ=45°+φ/2

因此土拱前缘线方程为

(2)

通过分析式(2)，发现在前述假设成立的条件下，桩间土拱的几何形态只与桩间净距和土体内摩擦角有关，而与拱后土压力无关。

2　地震作用下桩间挡板土压力计算

地震作用下挡墙的土压力计算是一个相当复杂的问题，可以采用的方法有拟静力法、位移法和拟动力法等，其中拟静力法由于概念清晰、计算方法较为简单、计算参数易于确定而被广泛采用，并积累了丰富的使用经验，是一种用静力学方法近似解决动力学问题的简化方法。S.OKABE和N.MONONBE等基于库伦土压力理论，考虑竖向和水平地震加速度的影响，认为在地震作用下，整个破坏楔体具有相同的加速度，采用最大地震加速度值，将地震作用简化为一个惯性力系附加在墙后滑动土体上，进而提出了计算挡土墙上的动土压力的Mononobe-Okabe公式。Mononobe-Okabe法假定墙后填土为无黏性土，取墙后土楔体进行整体受力平衡分析，只能求解土压力合力而无法得到土压力沿深度的分布情况，使得公式存在一定缺陷。笔者采用的水平层分析法是通过选取挡墙后水平土体微元建立静力平衡方程，得到墙后土压力的深度分布规律。它能很好地解决土压力分布和作用点位置的问题，是一种广泛应用于求解挡土墙土压力的方法。

2.1　挡板土压力求解方程的建立

笔者在采用水平层分析法推导地震作用下桩间挡板的土压力时，对挡板土压力分布及土体做出如下假定：① 拱体内侧屈服土体传给桩间挡板上的土压力在同一高度上均匀分布；② 忽略桩侧面与土体的摩阻力，这与前述忽略桩间摩擦土拱效应的假设一致；③ 将挡土墙后土体视为刚性，即满足拟静力法的使用条件。

基于忽略拱体自重、将土拱问题近似简化为沿桩长方向平面应变问题的假定，建立桩间挡板主动土压力计算模型，如图3(a)。在距地表某一深度z处取厚度为 dz的水平微元体薄片进行分析，如图3(b)。

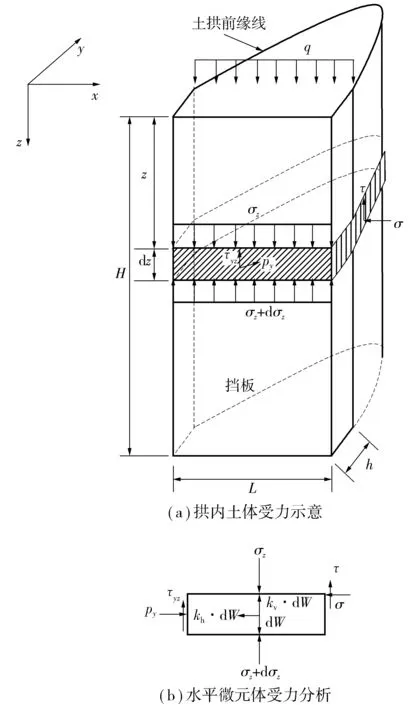
图3　桩间挡板主动土压力计算模型Fig. 3　Calculation model of active earth pressure on sheets between two piles

地震时，墙后土体受到的地震惯性力可以分解为水平和竖直2个分量，方向可正可负。作用在拱内屈服土体上的力有：土体重量dW；挡板主动土压力水平分量py和板与土体的摩擦力τyz；破裂面上剪应力τ和正应力σ；土体上、下面力σz和σz+ dσz；水平及竖向地震惯性力kh·dW、kv·dW。其中，kh、kv分别为水平向和竖直向地震加速度系数。规定各力的正方向如图3(b)。

由微元体水平向力的平衡条件可得

pL=khAγ+σL

(3)

由微元体竖向力的平衡条件可得

(4)

式(3)、(4)中：A为微元体上、下表面面积，m2；S为土拱前缘线弧长，m；γ为土体重度，kN/m3。

根据几何知识，求得

(5)

(6)

若取土体与挡板的摩擦角为δ，拱内土体侧压力系数为K，则有

τz=ptanδ

(7)

py=Kσz

(8)

考虑拱内屈服土体较为松散，可认为其黏聚力c=0，由Mohr-Coulomb破坏准则可得

τ=σtanφ

(9)

将式(7) ～ 式(9)代入式(3) 、式(4)，得

KσzL=khAγ+σL

(10)

(11)

联立式(10)、式(11)得到：

(12)

令

(13)

(14)

解微分方程(12)得

(15)

为求待定系数C，引入边界条件z=0，σz=q(q为坡顶荷载)，则

将C值代入式(15)，得

(16)

联立式(8)、式(16)，挡板不同深度处的土压力水平分量为

(17)

分析挡板土压力水平分量计算式(17)，可以发现此函数有一条渐近线

(18)

这表明挡板上的土压力水平分量py随深度增加趋于一个极值，而传统的Coulomb土压力理论和Rankine土压力理论都认为土压力沿深度线性增加，这说明考虑土拱效应的挡板土压力分布与Coulomb土压力理论和Rankine土压力理论有较大差别。

分析式(18)可以发现，土压力的极值与侧压力系数K、土体重度γ、土体内摩擦角φ、挡板与土体摩擦角δ、地震加速度系数kv、kh和桩间净距L有关，而与坡顶荷载q无关。

将py沿挡墙墙高积分得每延米挡板承受的主动土压力合力的水平分量Eah为：

(19)

2.2　土的侧压力系数K的确定

土的侧压力系数K可由挡板与土体接触处的应力状态来确定，由于成拱过程中拱内土体已经松散屈服，因此忽略墙后土体与挡板的黏结力。由Mohr-Coulomb强度理论可知，此时强度包络线为过原点的直线。用Mohr圆表示的边界点土体应力状态如图4。

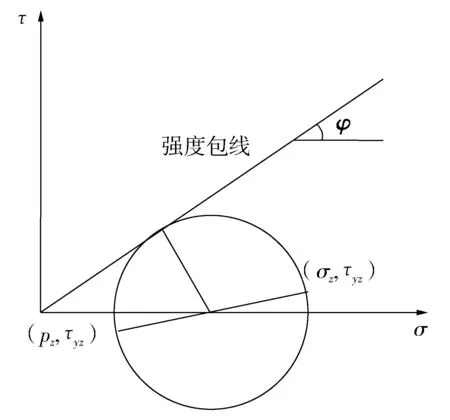
图4　用Mohr圆表示的挡板边界土体应力Fig. 4　Soil stress at the boundary of baffle described by Mohr circle

则有

(20)

将τyz=pytanδ、py=Kσz代入式(20)，可得

K24tan2δ+cos2φ-2K1+sin2φ+

cos2φ=0

(21)

式(21)为一元二次方程式，其解的判别式为

Δ=16sin2φ-tan2δcos2φ

(22)

因为δ≤φ、Δ≥0，所以式(21)一定有实数解

(23)

由于K≤ 1，所以

(24)

当桩间挡板光滑时，即δ=0，则有

(25)

即为Rankine主动土压力系数。

至此，如果给定土体参数、支护结构参数、坡顶荷载、地震加速度系数等参数，即可计算地震作用下考虑土拱效应的挡板的主动土压力。

3　挡板土压力分布及影响因素分析

土压力沿深度的分布情况和土拱效应的发挥是挡板土压力计算中的2个关键问题。以某工程为算例，将文中方法与卸荷拱法、拟化筒仓法、边坡规范法进行对比，研究土压力的分布和土拱效应的发挥情况。

3.1　挡板土压力的分布及随土体内摩擦角的变化

选取支护桩矩形截面长1.0 m、宽0.6 m，桩板挡墙支护高度H=5 m，桩间净距L=4 m。墙后土体内摩擦角φ=32°，为无黏性土，土体重度γ=18.0 kN/m3，墙背摩擦角取δ=φ/3。

3.1.1卸荷拱法

叶晓明[11]基于卸荷拱原理导出了桩间挡板土压力计算公式：

(26)

3.1.2拟化筒仓法

重庆市地方标准DB 50/5029—2004《地质灾害防治工程设计规范》将桩间支档结构、桩、土拱拟化为一个筒仓，提出了一种计算桩间支档结构土压力的方法。若偏安全地忽略挡土板厚度，则挡土板土压力按式(27)计算：

(27)

式中：α=(Lh+0.25L2)/(2h+2.414L)，k=tanφ·tan245°-φ/2。

3.1.3挡板土压力随深度和土体内摩擦角的变化

为了研究挡板土压力沿深度的分布和随土体参数的变化情况，将文中方法与卸荷拱法和拟化筒仓法进行对比。由于卸荷拱法和拟化筒仓法均无法考虑地震作用的影响，因此，暂取kv=kh=0。将文中法、卸荷拱法、拟化筒仓法、Coulomb土压力这4种土压力随深度变化曲线绘制在图5(a)中。同时，取计算点深度z=5 m，内摩擦角φ=14～50°，将各理论的计算土压力值随内摩擦角的变化关系绘制于图5(b)中。

从图5(a)可以看出，桩间土拱效应的存在可以显著减小挡板所受的土压力，土压力呈现明显的非线性分布，这一趋势与Coulomb土压力理论有明显不同；从图5(b)可以看出，随着土体内摩擦角的增大，4种方法所得土压力值均随土体内摩擦角的增大而减小，挡板土压力值趋近于Coulomb土压力，这说明土体内摩擦角较大时，土体自稳能力较强，限制了桩间土拱效应的发挥。

计算点深度和土体内摩擦角是影响土压力大小的最主要因素。综合分析图5可以推断：文中方法所得土压力与卸荷拱法和拟化筒仓法具有类似的变化趋势；在土体内摩擦角较小时，文中方法所得土压力值介于卸荷拱法和拟化筒仓法之间；随着土体内摩擦角的增大，文中方法所得土压力值略大于卸荷拱法和拟化筒仓法；对于本算例，在土体内摩擦角约大于38°时，文中方法所得土压力值略大于卸荷拱法和拟化筒仓法。

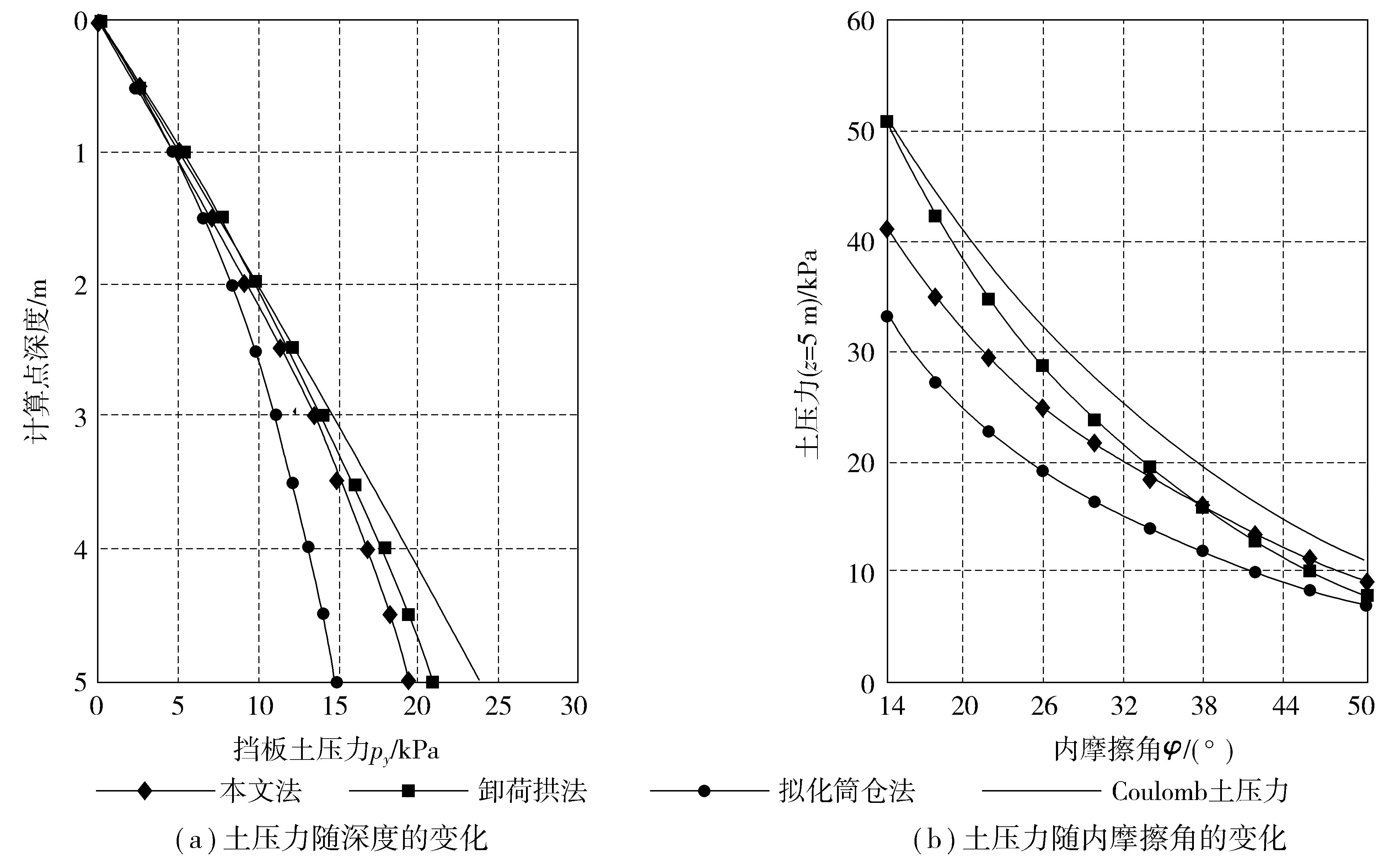
图5　挡板土压力随深度和土体内摩擦角的变化Fig. 5　Variation of earth pressure on sheets changing with depth and soil internal friction angle

3.2　地震作用和桩间距对挡板土压力的影响

3.2.1边坡规范法

GB 50330—2013《建筑边坡工程技术规范》提出，考虑地震作用时，作用于支护结构上的地震主动土压力可按式(28)计算：

(28)

考虑墙背直立、坡顶填土面水平的情况，将式(28)中Ka进行整理后得：

Ka={Kq[cos(δ+ρ)+sin(φ+δ)sin(φ-ρ)]+

2ηcosφcosρsin(φ+δ)-2[(Kqsin(φ-ρ)+

ηcosφcosρ)×〔Kqcos(δ+ρ)sin(φ+δ)+

ηcosφcosρ〕]0.5}/[cosρcos2(φ+δ)]

(29)

3.2.2桩间距对土拱效应的影响

为了研究地震作用下土拱效应对挡板土压力的影响，将文中方法与边坡规范法进行对比。取地震加速度系数kv=0、kh=0.20，查表得此时的地震角ρ=3°。取坡顶荷载q=10 kPa，分别采用文中方法、边坡规范法计算不同桩间距情况下每延米挡板承受的地震动土压力合力的水平分量Eah，计算结果如图6。

图6　地震作用和桩间距对挡板土压力的影响(q=10 kPa)Fig. 6　Effects of earthquake and pile spacing on earth pressure of sheet(q=10 kPa)

从图6可以看出，文中方法计算所得土压力显著小于边坡规范法，这是因为边坡规范法没有考虑桩间土拱效应的影响。由此可见，桩间土拱效应可以显著降低挡板承受的主动土压力。若以本算例中桩间净距2.5 m为参照，每延米主动土压力减小约16%，此时若采用传统的土压力理论设计桩间挡板势必造成较大的资源浪费。同时可以看出，桩间距小于4 m时，土拱效应较强。随着桩间净距的增加，桩间土拱效应越来越弱，挡板土压力值逐渐趋近于传统土压力算法。这与TB 10025—2006《铁路路基支挡结构设计规范》提出的考虑土拱效应时，取“抗滑桩桩中心距5～8 m、净距2～4 m”的结论类似。

另外，对于本算例，边坡规范法所得地震主动土压力放大系数约为1.11，文中方法约为1.14，两种计算方法所得地震放大系数非常接近。这说明文中方法有效地考虑了地震作用的影响。

由此可见，文中方法既能够考虑地震作用和土拱效应，又可以反映土压力随深度的变化情况，解决了现行边坡规范计算地震主动土压力时不能考虑土拱效应的缺陷。

3.2.3地震加速度系数组合对土压力的影响

保持算例中支护结构和土体力学参数不变，取q=0，使kh、kv分别在(-0.3 ～ +0.3)的范围内变化，研究不同的地震加速度系数组合对桩间挡土构件主动土压力的影响。地震作用下挡板土压力合力的水平分量Eah的增大系数与地震加速度系数kh、kv的三维关系如图7。

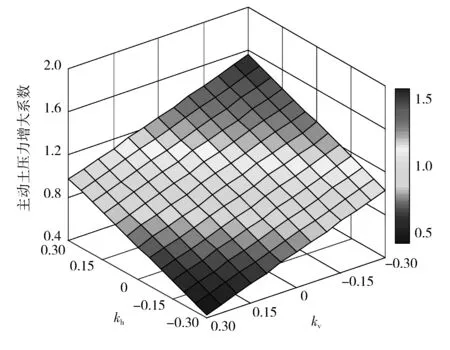
图7　土压力增大系数与地震加速度系数kh、kv的关系Fig. 7　Relationship between magnified coefficient of earth pressure and earthquake acceleration coefficient kh，kv

基于前述建立挡板主动土压力计算模型时规定的水平、竖向地震加速度正方向〔图3(b)〕，从图7可以看出，水平地震力的最不利方向朝向挡板，而竖向地震力的最不利方向竖直向下。可以理解为竖向地震起到了增大土体重度的作用；地震作用下的挡板土压力显著大于非地震作用下的土压力，并随地震加速度系数的增大而增大；土压力增大系数与地震加速度近似呈线性关系；三维曲面近似为一斜面，说明水平、竖向地震力对土压力的贡献几乎相当。

4　结　论

通过建立考虑地震作用的挡板土压力计算模型，提出了考虑土拱效应的挡板土压力计算方法。通过与卸荷拱法、拟化筒仓法、边坡规范法的对比及地震作用影响分析，得到以下结论：

1) 考虑桩间土拱效应的挡板土压力分布与传统土压力理论有明显不同，土压力沿深度呈非线性分布，大小随深度增加将趋于稳定；随着土体内摩擦角的增大，土拱效应有减弱的趋势。

2) 文中方法所得土压力与卸荷拱法和拟化筒仓法具有类似的变化趋势；在土体内摩擦角较小时，文中方法所得土压力值介于卸荷拱法和拟化筒仓法之间；随着土体内摩擦角的增大，文中方法、卸荷拱法、拟化筒仓法所得土压力值趋于一致，但文中方法值略大。

3) 文中方法既能够考虑地震作用和土拱效应，又可以反映土压力随深度的变化情况，解决了现行边坡规范计算地震主动土压力时不能考虑土拱效应的缺陷。

4) 桩间土拱效应可以显著降低挡板承受的主动土压力。桩间距小于4 m时，土拱效应较强；随着桩间净距的增加，桩间土拱效应越来越弱，挡板土压力值逐渐趋近于传统土压力算法。

5) 水平、竖向地震力会显著放大挡板土压力，两个分量对土压力的贡献几乎相当；土压力增大系数与地震加速度近似呈线性关系。

6) 笔者在建立桩间挡板土压力计算模型时将土拱效应简化为平面应变问题、采用拟静力法分析地震作用下桩间挡板的土压力。但实际上土拱效应是一个复杂的三维问题、拟静力法计算挡墙土压力存在一定的误差，因此需要通过后续的实验以确定这种简化带来的误差。

参考文献(References)：

[1] HASSIOTIS S，CHAMEAU J L，GUNARATNE M.Design method for stabilization of slopes with piles[J].JournalofGeotechnicalandGeoenvironmentalEngineering，1997，123(4)：314-323.

[2] TERZAGHI K.TheoreticalSoilMechanics[M].New York：John Wiley & Sons，1943.

[3] 黄治云，张永兴，董捷.桩板墙土拱效应及土压力传递特性试验研究[J].岩土力学，2013，34(7)：1887-1892.

HUANG Zhiyun，ZHANG Yongxing，DONG Jie.Experimental study of soil arching and transfer behavior of earth pressure about sheet-pile walls[J].RockandSoilMechanics，2013，34(7)：1887-1892.

[4] WANG Mingmin，WU Shuguang，WANG Guilin.Limit analysis method for active earth pressure on laggings between stabilizing piles[J].JournalofMountainScience，2017，14(1)：196-204.

[5] 贾海莉，王成华，李江洪.基于土拱效应的抗滑桩与护壁桩的桩间距分析[J].工程地质学报，2004，12(1)：98-103.

JIA Haili，WANG Chenghua，LI Jianghong.Analysis of pile spacing between anti-sliding piles and pertaining piles in accordance with soil arching effect[J].JournalofEngineeringGeology，2004，12(1)：98-103.

[6] 蒋良潍，黄润秋，蒋忠信.黏性土桩间土拱效应计算与桩间距分析[J].岩土力学，2006，27(3)：445-450.

JIANG Liangwei，HUANG Runqiu，JIANG Zhongxin.Analysis of soil arching effect between adjacent piles and their spacing in cohesive soils[J].RockandSoilMechanics，2006，27(3)：445-450.

[7] 杨明，姚令侃，王广军.桩间土拱效应离心模型试验及数值模拟研究[J].岩土力学，2008，29(3)：817-822.

YANG Ming，YAO Lingkan，WANG Guangjun.Study of centrifuge model tests and numerical simulation on soil arching in space of piles[J].RockandSoilMechanics，2008，29(3)：817-822.

[8] 邱子义，韩同春，豆红强，等.桩后及桩侧土拱共同作用的抗滑桩桩间距分析[J].浙江大学学报(工学版)，2016，50(3)：559-565.

QIU Ziyi，HAN Tongchun，DOU Hongqiang，et al.Analysis of spacing between anti-slide piles considering soil arch on lateral sides and back[J].JournalofZhejiangUniversity(EngineeringScience)，2016，50(3)：559-565.

[9] HE Yi，HAZARIKA H，YASUFUKU N，et al.Estimation of lateral force acting on piles to stabilize landslides[J].NaturalHazards，2015，79(3)：1981-2003.

[10] WU Junjie，LI Changdong，LIU Qingtao，et al.Optimal isosceles trapezoid cross section of laterally loaded piles based on friction soil arching[J].KSCEJournalofCivilEngineering，2017，21(7)：2655- 2664.

[11] 叶晓明.柱板结构挡土墙板上的土压力计算方法[J].地下空间，1999，19(2)：142-146.

YE Xiaoming.Calculation of soil pressure on column-panel structure type retaining wall[J].UndergroundSpace，1999，19(2)：142-146.

[12] PERKO H A，BOULDEN J J.Lateral Earth Pressure on Lagging in Soldier Pile Wall Systems[J].TheJournaloftheDeepFoundationsInstitute，2008，2(1)：46-54.

[13] 梁瑶，蒋楚生，李庆海，等.桩间复合结构土拱效应试验与受力机制研究[J].岩石力学与工程学报，2014，33(增刊2)：3825-3828.

LIANG Yao，JIANG Chusheng，LI Qinghai，et al.Analysis of stress mechanism of pile composite structure based on soil arch test[J].ChineseJournalofRockMechanicsandEngineering，2014，33(Sup2)：3825-3828.

[14] 赵晓彦，吴兵，李登峰，等.考虑桩间水平土拱效应的边坡桩间墙组合结构受力计算方法[J].岩土工程学报，2016，38(5)：811-817.

ZHAO Xiaoyan，WU Bing，LI Dengfeng，et al.Load calculation method for retaining wall between piles considering horizontal soil arching effects[J].ChineseJournalofGeotechnicalEngineering，2016，38(5)：811-817.

[15] 董捷.悬臂桩三维土拱效应及嵌固段地基反力研究[D].重庆：重庆大学，2009.

DONG Jie.StudyonThree-DimensionalSoilArchingEffectofCantileverPilesandGroundResistingForceActedonItsBuild-inZone[D].Chongqing：Chongqing University，2009.

[16] 刘力生.抗滑桩桩间土拱动力稳定性试验及土压力计算分析[D].重庆：重庆大学，2015.

LIU Lisheng.DynamicStabilityTestofSoilArchingandStudyofEarthPressureTheoryonAnti-slidePiles[D].Chongqing：Chongqing University，2015.