圆台型螺旋能量桩换热特性的模拟分析与验证
2018-04-11刘亚姣黄光勤杨小凤庄春龙
刘亚姣,黄光勤※,卢 军,杨小凤,庄春龙
圆台型螺旋能量桩换热特性的模拟分析与验证
刘亚姣1,黄光勤1※,卢 军2,杨小凤1,庄春龙1
(1. 陆军勤务学院军事设施系,重庆 401311; 2. 重庆大学城市建设与环境工程学院,重庆 400045)
为了减少地源热泵的热干扰、提高其换热效率,该文提出了一种新型“圆台型螺旋能量桩(truncated cone helix energy pile,CoHEP)”。同时为了更加准确地模拟新型圆台型螺旋能量桩的换热特性,综合考虑初始土壤温度的不均匀性和土壤上表面动态边界条件,建立了三维数值模型,分析了不同锥角下圆台型螺旋能量桩的换热特性。结果表明:圆台型螺旋能量桩沿水流方向可以分成4个换热阶段:入口阶段→热短路阶段→小温差阶段→出口阶段。圆台型螺旋能量桩的底部热干扰现象较为严重,且锥角越大,底部热干扰越明显。相反,由于顶部螺旋半径较大,热干扰效应较弱。圆台型螺旋能量桩的单位管长换热量随着锥角的增加而线性增大,当系统运行时间为12 h时,锥角从0增加到10°再增加到20°,单位管长换热量增长率分别为2.54%和3.53%。新型圆台型螺旋能量桩单位管长换热量大于传统圆柱型螺旋能量桩,20°锥角条件下的单位管长换热量比传统圆柱型螺旋能量桩高了约6.16%。通过对新型圆台型螺旋能量桩的换热特性进行探析,相对于传统圆柱型螺旋能量桩,提升了换热效率,同时为后续的推广应用和工程设计奠定了理论基础。
热泵;换热;数值模拟;螺旋能量桩
0 引 言
螺旋能量桩是一种应用于地源热泵系统的新型的地下热交换器[1]。它通常埋设在建筑物的混凝土桩基础上,与建筑结构相融合。与传统的U型和W型能量桩相比[2-4],螺旋能量桩在同一深度下具有较大的传热面积[5-7]。对于传统的螺旋能量桩,换热管缠绕在圆柱壁面上,在本文中被称为“圆柱型螺旋能量桩(CyHEP,cylinder helix energy pile)”。
目前关于圆柱型螺旋能量桩的研究主要集中在进行一定程度简化的解析解模型上。Man等[8]针对传统圆柱型螺旋能量桩提出了无限长和有限长的圆柱热源模型,并推导得出其温度场表达式,但是该模型不能分析管壁温度的变化规律。Zhang等[9]以圆柱热源模型为基础,提出了考虑不同螺距的线圈热源模型,并推导计算出了线圈热源模型解析解形式的表达式。该模型可以计算分析管壁的温度变化。Wang等[10]考虑了能量桩内外岩土热物性差异的影响,并在此基础上提出了圆柱热源模型和线圈
热源模型的解析解表达式。Li等[11]综合了圆柱热源模型和线圈热源模型,提出了考虑圆柱型螺旋能量桩复杂结构的三维解析解模型,使解析解模型更加贴合实际。通过分析可以发现,尽管解析解模型的求解计算较为便捷,但是由于各类假设条件的存在,导致与实际工况的差异较大。比如解析解模型并没有考虑螺旋管内部水的流动,只是假定了螺旋管的单位管长发热量[12-13];同时也认为土壤的初始温度是均匀一致的,这与实际情况不相符;另外,几乎所有解析解模型都没有考虑土壤上表面动态环境的影响。
除了解析解模型外,一些学者还研究了圆柱型螺旋能量桩的数值解模型。Bezyan等[14]建立了圆柱型螺旋能量桩的三维数值传热模型,并利用商业数值模拟软件FLUENT 6.3.26计算分析了不同螺距下的换热性能。但是该模型假设土壤初始温度是均匀的,并且土壤上表面边界温度为恒定值。Jalaluddin等[15]利用计算流体力学软件ANSYS FLUENT14.5对圆柱型螺旋能量桩进行三维数值模拟,并分析了其换热和沿程压降规律。Xiang等[16]针对圆柱型螺旋能量桩,通过对三维模型进行降维简化,建立了新的数值解模型,该模型包括了管内流体域的一维瞬态子模型和管外固体域的一维瞬态子模型。通过分析发现,圆柱型螺旋能量桩的三维数值解模型较为复杂,研究人员总是做出一定的简化处理,导致与实际情况有一定的偏差。例如,大多数数值解模型没有考虑土壤初始温度的不均匀性和土壤上表面的动态环境参数[17-20];还有一些研究人员把复杂的三维模型简化为一维或二维模型。
虽然与U型和W型能量桩相比,螺旋能量桩在同 一深度下具有较大的传热面积。但是仍然有相关研究发 现[21-23],由于相邻螺旋线圈之间的距离较小,传统圆柱型螺旋能量桩的热干扰作用较为剧烈,极大地限制了换热效率的提升。但是目前研究人员主要是研究传统圆柱型螺旋能量桩的数学模型,较少关注其热干扰效应和沿程换热特性。因此,为了减少热干扰、提高换热效率,本文提出了一种新型圆台型螺旋能量桩,如图1所示。圆台型螺旋能量桩作为地源热泵系统中最核心的地下换热部件,可依托建筑基础,埋设于建筑桩基内部,可较大程度节约钻孔费用,减少系统初投资。但通过对实际工程调研分析发现,由于建筑桩基数量有限,现有实际工程多采用桩基埋管辅以室外钻孔埋管才能满足负荷需求,即在室外空地钻孔埋设“圆台型螺旋能量桩”,本文所研究圆台型螺旋能量桩就是基于此背景工况开展的,需要考虑上表面动态环境参数的影响。
针对该新型圆台型螺旋能量桩,课题组在前期进行了初步的研究[24]。主要是通过建立三维解析解模型来对其热干扰和换热特性进行研究。但是存在如下几点假设:土壤初始温度均匀;土壤上表面边界条件为定值;螺旋管设定一个恒定的单位长度发热量。显然这些假设会导致与实际情况存在偏差。更重要的是,该解析解模型不能用于分析螺旋管的沿程换热特性。
在前期工作的基础上,为了更加准确地模拟新型圆台型螺旋能量桩的换热特性,本文综合考虑初始土壤温度的不均匀性和土壤上表面动态边界条件,建立了三维数值模型。并进行了相关试验,验证模型的准确性。
1 圆台型螺旋能量桩的数值解模型
该新型“圆台型螺旋能量桩(CoHEP,truncated cone helix energy pile)”的几何特点在前期成果中已做了相关介绍[24]。前期研究发现,圆台型螺旋能量桩采用上下颠倒埋设的2种方式,其单位管长换热量相差不大。同时考虑到挖孔钻井施工的可行性及安全性,采用上大下小的埋设方式,一方面便于施工开挖,另一方面可以使井壁具有一定的倾斜角度,降低了开挖过程中井壁坍塌的风险,所以本文提出的圆台型螺旋能量桩均采用上大下小的埋设方式,具体结构如图1所示,螺旋管缠绕在圆锥壁面上,且螺旋半径随着埋深的增加而线性减小,螺旋线遵循以下方程:
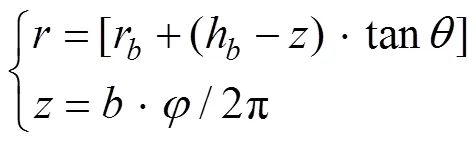
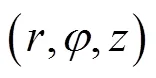
由于圆台型螺旋能量桩的几何结构复杂,实际尺寸的三维模拟计算工程量庞大,对硬件要求较高。为了提高模拟计算的效率,本文基于相似原理建立了圆台型螺旋能量桩的缩比尺寸模型。这将有助于实现圆台型螺旋能量桩的高效长期模拟。同时,还模拟计算了螺旋管沿程水温变化,进而分析其沿程换热特性。

注:hb为地表面距能量桩底面的距离,m;ht为地表面距能量桩顶面的距离,m;rt为能量桩顶面螺旋半径,m;rb为能量桩底面螺旋半径,m;b为深度方向的螺距,m;d为轴向相邻管段间的距离,m;θ为锥角,(°)。
1.1 缩比模型
本文采用相似性原理对原型尺寸模型进行缩小。由相似性原理可知,为了使原型和缩比模型的热性能相似,2个模型的相似性指标必须等于1。因此在设计缩比模型时,在原型基础上采用长度尺度系数对其进行类似换算,土壤和流体的热物理参数与原型相同。根据传热相似理论,由于缩比模型是按照同一长度尺度系数对原型进行等比例缩小,且原型和缩比模型的土壤和流体的热物性参数均相同,所以经过计算可知原型和缩比模型中的Nu、Fo和Re数是相等的。余延顺等针对地源热泵系统原型和缩比模型之间的关系进行探究,得到二者之间的时间关系是[25]:
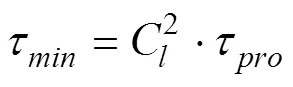
因此,通过对原型尺寸进行缩小,与原型模拟的长时间计算周期相比,可以在相对较短的时间内获得计算结果,大大减少对计算机配置的要求。通过以上分析,根据相关标准规范及工程实际确定原型尺寸[26],进而确定缩比模型相应的主要参数,如表1所示。
在本文中,模型均由软件Solidworks构建,并导入软件Workbench中划分网格。由于螺旋管周围的温度变化较大,需要更高的计算精度,管周围的网格进行了部分加密处理。同时,随着半径的增大,土壤温度变化越来越小,所以网格大小沿径向逐渐增大。同时进行网格无关性验证,针对缩比模型选取4种不同的网格尺度大小分别进行网格划分,得到4种不同的网格数量(253万、350万、397万和434万)如图2所示,从图中可以看出,当网格数量从253万逐步增大到434万时,分别模拟运行12 h后出口温度值的变化不大,说明选取的4种网格数量对计算结果的影响很小,可认为253万网格数量已经达到网格无关,因此后续模拟选取253万的网格数量进行模拟计算。

表1 原型和缩比模型的主要参数
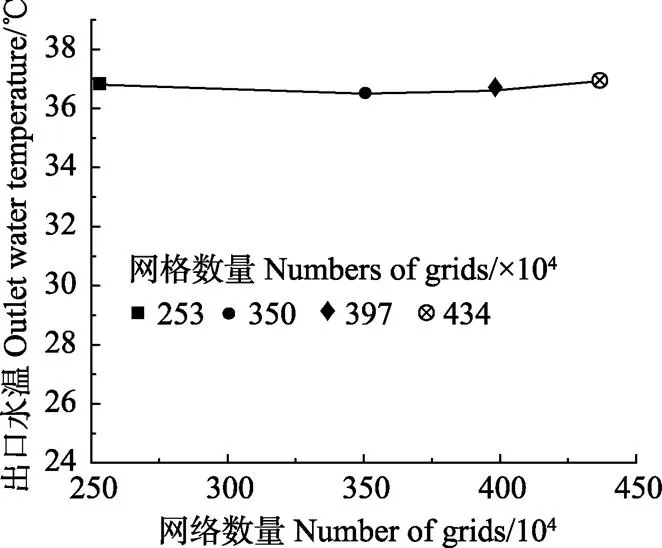
图2 网格无关性验证
模拟的主要参数如表2所示,各参数均是依据缩比试验平台测得,与验证试验一致。其中导热系数通过“球体法”测得,比热容通过“混合量测法”测得,螺旋管的相关参数由生产厂商提供[27]。

表2 数值模拟的主要参数
1.2 控制方程
对于地埋管换热器,管内流体与管壁之间属于强迫对流换热,流体处于湍流状态。本文中假设土壤为均匀各向同性的固体,同时不考虑地下水渗流的影响。
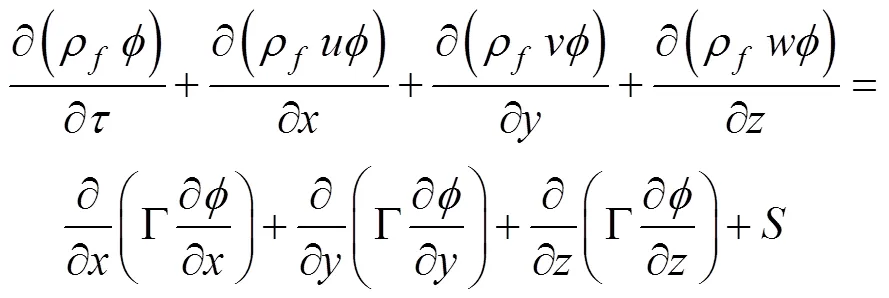
由于土壤被视为均质各向同性的固体,且不考虑地下水渗流的影响,所以土壤中只存在导热作用。土壤中的热控制方程如式(4)所示:
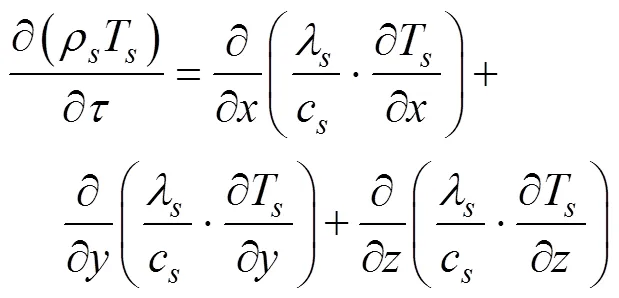
式中,ρ为土壤密度,kg/m3;c为土壤比热容,J/(kg·K);λ为土壤导热系数,W/(m·K);T为土壤温度,℃。
1.3 初始及边界条件
由于螺旋能量桩埋深较浅,通常埋设于地表以下10~20 m处,因此地埋管的传热受土壤上表面环境条件的影响较大。特别地,由于新型圆台型螺旋能量桩的顶部螺旋直径比传统的圆柱型螺旋能量桩大,靠近土壤上表面的换热管面积更大,因此,外界动态边界条件对新型圆台型螺旋能量桩的换热影响不容忽视。在开展的数值模拟验证试验中,记录了试验运行12 h (720 min)期间土壤上表面处的动态环境温度,并通过数据拟合得到土壤上表面动态环境温度的函数表达式为:
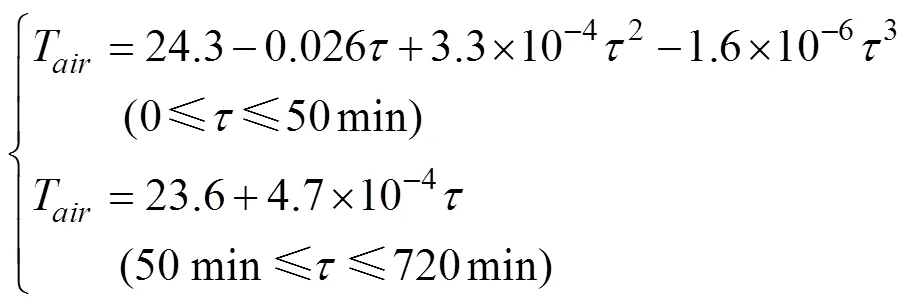
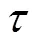
初始土壤温度受外界气温和太阳辐射的共同作用,因此地温与深度和时间存在相应的关系,严重影响着地埋管的换热性能,是理论计算中最重要的参数之一。特别是对于螺旋能量桩,由于其埋深较浅,初始土壤温度分布不均匀,考虑其深度方向的温度不均匀性将使模型更加贴合实际情况。在开展的数值模拟的验证试验中,记录了初始时刻在圆柱形土壤箱(直径1.8 m×高1.5 m)深度方向上的土壤温度分布数据,并通过拟合得到了初始时刻土壤温度的函数表达式如下:
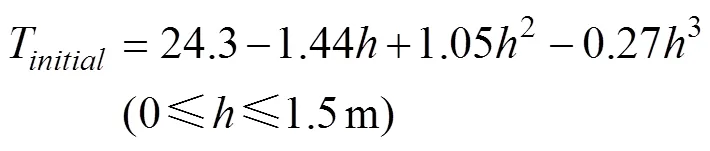
式中T为初始时刻(2017年9月21日9:08)土壤温度,℃;为地下深度,m。
根据上述拟合函数方程,利用C语言编写自定义函数程序(UDF,user defined function)对土壤上表面动态环境温度和初始土壤温度进行定义,并编译纳入数值计算模型。对于模型的其它边界条件,将圆柱形土壤模型的顶面、底面和四周定义为wall,螺旋管入口定义为Velocity-Flow-Inlet,出口定义为Pressure-Outlet,螺旋管和土壤定义为Solid,螺旋管内部定义为Fluid。
1.4 FLUENT软件设置
本文使用商用CFD模拟软件ANSYS_FLUENT进行数值模拟计算,由于螺旋管长20 m,远远大于螺旋管内径0.005 m,属于细长区域传热模型,选择3D双精度求解器进行计算。根据验证试验确定管内流体、螺旋管和土壤的热物性参数(见表2)。依据实际工程情况将埋设有圆台型螺旋能量桩的圆柱型土壤箱(见图3a)的顶面定义为传热边界,底面和四周定义为绝热边界条件以避免外界的影响。求解采用SIMPLEC算法和二阶迎风格式进行计算。
2 数值模拟的试验验证
为了验证第1节所建立数值模拟模型的准确性开展了验证试验,试验系统如图3a所示,包括埋有圆台型螺旋能量桩的圆柱形土壤箱(直径1.8 m×高1.5 m)、流量计(型号:LZB-6,量程:6~60 L/h,精度:2.5)、水泵(型号:MP-6R)、恒温水箱、热电偶(型号:K型)和数据采集仪(型号:SH-X)等。系统中的水在恒温水箱中被持续加热,然后通过水泵输送到圆台型螺旋能量桩,在能量桩中热量由热水散入到低温土壤中,数据采集仪记录出口水温并监测其变化情况。测试从2017年9月21日9:08开始,运行12 h。有关参数设定如表1和表2所示。此外,圆柱形土壤箱的外测和外部管道均包裹着保温材料,以减少外界环境的干扰[28-30]。
为了验证数值模型的准确性,将通过数值模拟计算得到的出口水温与数据采集仪记录的实际出口水温进行比较,如图3b所示。从图中可以看到,出口水温随时间逐渐升高并最终趋于稳定。模拟值与实测值吻合较好,两者之间的最大差异出现在160 min时刻,经计算差异为1.5%,在数值模拟验证的允许误差范围5%以内[31]。由以上分析可知,模拟结果与试验测试结果吻合较好,数值模拟计算的准确性得到验证。
3 结果与分析
3.1 换热能力分析
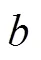

图3 数值模拟的试验验证
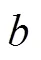
图4所示为不同锥角条件下圆台型螺旋能量桩换热能力随时间的变化曲线。图4a显示了3种锥角条件下模拟出口水温随运行时间的变化情况,可以发现出口水温随时间逐渐增大并最终达到稳定状态。相应的,图4b显示了3种锥角条件下单位管长换热量随运行时间的变化情况,结果表明,单位管长换热量随着时间的推移而逐渐减小,最终达到稳定状态。分析造成这一趋势的主要原因为:系统运行初期,管内流体与土壤的温差最大,换热较为充分,因此在系统运行初期单位管长换热量较大。然而随着系统的持续运行,能量桩的热影响范围逐渐扩大,土壤的热阻成为传热过程的主要矛盾,导致传热效率降低。经过一段时间的换热后,土壤中的热量持续积聚,管内流体与土壤的温差持续减小,导致单位管长换热量持续降低。之后当土壤温度场趋于稳定时,换热性能也逐渐稳定。
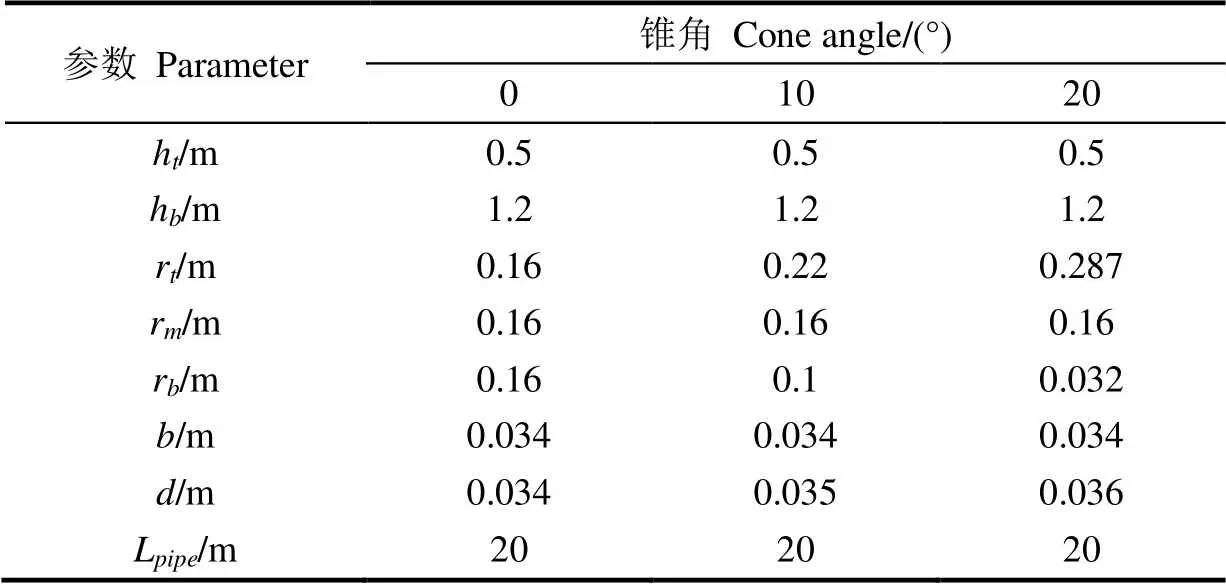
表3 不同锥角圆台型螺旋能量桩尺寸参数

图4 圆台型螺旋能量桩换热能力随时间的变化曲线
如图5所示,单位管长换热量随着锥角的增大而线性增大。当系统运行时间分别为4、8、12 h时,锥角为0°时,单位管长换热量在不同时刻分别为4.46、3.34、2.76 W/m。锥角为10°时,单位管长换热量在不同时刻分别为4.52、3.42、2.83 W/m。在20°锥角情况下,单位管长换热量在不同时刻分别为4.74、3.52、2.93 W/m。随着锥角的增大,圆台型螺旋能量桩单位管长换热量也就相应增大。当系统运行时间为12 h时,锥角从0°增加到10°再增加到20°,单位管长换热量增长率分别为2.54%和3.53%。分析可知,随着圆台型螺旋能量桩锥角的增大,其单位管长换热量也随之增加,且呈线性增长趋势。可见在一定范围内增大圆台型螺旋能量桩的锥角可增加单位管长换热量,提高其换热能力。
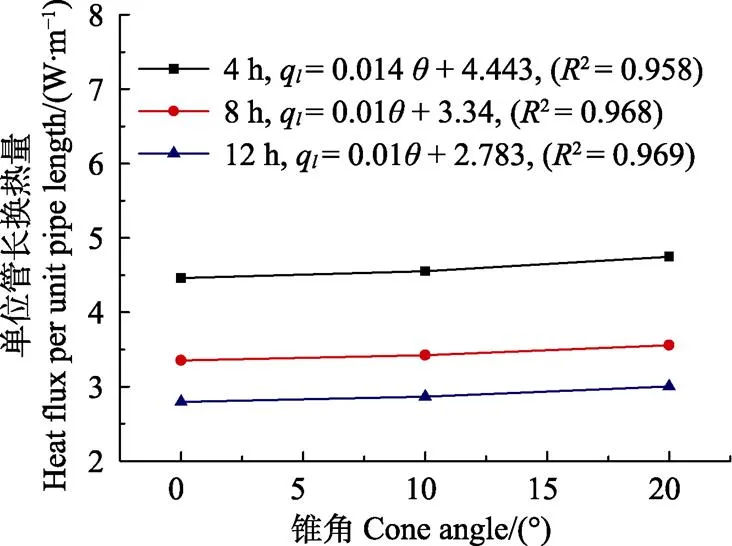
图5 单位管长换热量与锥角之间的关系
3.2 沿程换热特性分析
图6所示为不同锥角(0°、10°、20°)条件下单位管长换热量沿管长方向的变化情况。根据圆台型螺旋能量桩的几何特性,结合图6所示的沿程换热特性,可以将螺旋管沿水流方向分为4个不同且连续的换热阶段:
1)入口阶段S1(约0~2.5 m):该阶段位于螺旋能量桩的顶部,与上层的覆土区域之间接触,当高温流体经过这一阶段时,热量除了沿经向传递外,还有一部分沿轴向传入无热干扰存在的覆土区域。同时,由于圆台型能量桩顶部的螺旋半径最大,半径方向的热干扰最小,热堆积最小,所以该阶段换热能力最大。
2)热短路阶段S2(约2.5~10 m):随着流体流过入口阶段,由于土壤的热容量有限,热量积聚在土壤中无法快速散去,螺旋管之间沿轴向存在热短路现象,导致热量主要沿经向传递,所以该阶段的换热性能有所下降。
3)小温差阶段S3(约10~17.5 m):当热短路阶段结束后,管道内的流体温度持续的减小,导致流体与周围土壤间的换热温差减小,换热效率降低。同时,由于圆台型螺旋能量桩下部螺旋半径较小,由于热量的积聚,在经向和轴向均存在严重的热干扰效应。因此在该阶段换热能力进一步下降。
4)出口阶段S4(约17.5~20 m):和入口阶段相类似,该阶段的螺旋管与能量桩下部区域的土壤相接触,轴向热干扰相对较小,有一部分热量沿轴向传入能量桩下方土壤。因此在该阶段换热能力稍有提升。
从图6可以看出,在入口阶段和热短路阶段,0°锥角下螺旋管的单位管长换热量最小,20°锥角下螺旋管的单位管长换热量最大。这是因为20°锥角条件下圆台型螺旋能量桩的顶部螺旋半径最大,径向热干扰较小,换热能力较大。相反,在小温差阶段和出口阶段,0°锥角下的单位管长换热量最大,20°锥角下的单位管长换热量最小。原因在于圆台型螺旋能量桩在20°锥角条件下的底部螺旋半径最小,经向的热干扰较大,导致传热效率较低。
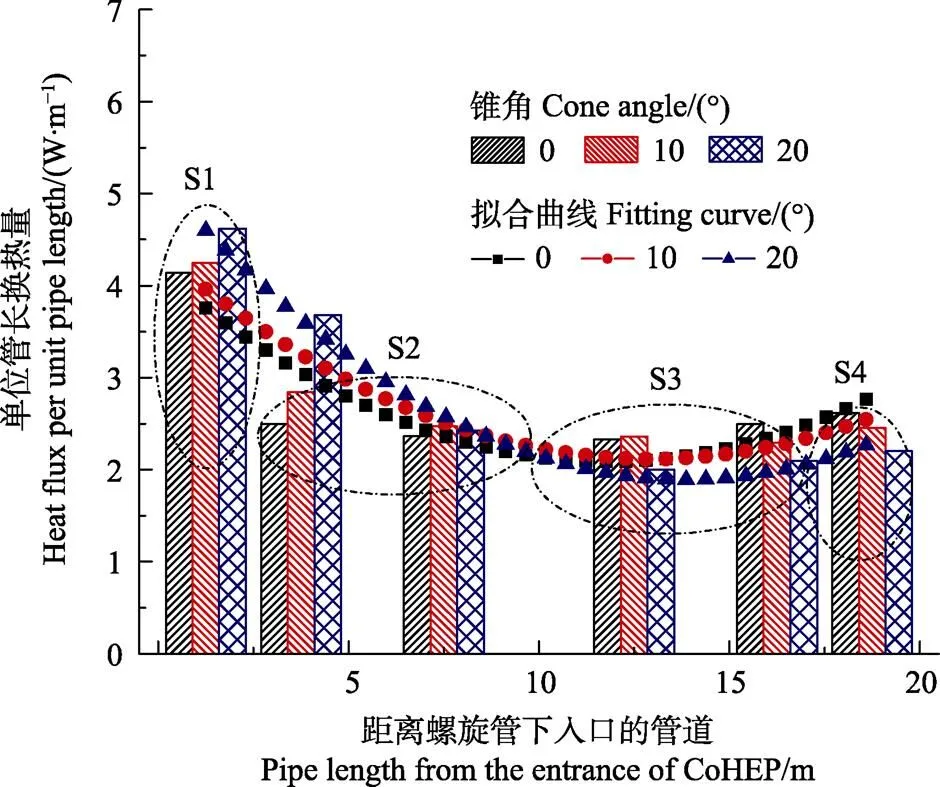
注:S1—入口阶段;S2—热短路阶段;S3—小温差阶段;S4—出口阶段。
综上所述,新型圆台型螺旋能量桩的顶部螺旋半径大于传统圆柱型螺旋能量桩,导致径向热干扰小,换热能力强。虽然圆台型螺旋能量桩底部的热干扰现象严重,换热能力低,但入口阶段和热短路阶段的流体温度(换热温差)高于后2个阶段,因此前个阶段的换热能力远远大于后个阶段的换热能力,承担了整个螺旋能量桩的主要换热量。所以整体而言,锥角越大,换热性能越优越。而且,在深度方向的螺距()相同的条件下,圆台型螺旋能量桩轴向相邻管段之间的距离()明显大于传统圆柱型螺旋能量桩,且锥角越大,越大,可以有效地减少轴向热干扰,提高换热效率。因此,新型圆台型螺旋能量桩的单位管长换热量大于传统圆柱型螺旋能量桩,且20°锥角条件下单位管长换热量最大,比0°条件下(传统圆柱型螺旋能量桩)高了6.16%。
3.3 热响应分析
图7所示为不同锥角条件下的管壁温度分布云图。从图中可以看出,与0°锥角相比,20°锥角条件下的高温流体几乎全部分布在螺旋半径较大的能量桩上部,由于上部区域的热干扰效应相对较小,同时高温流体可以直接与上方覆土区域进行热量交换,提升了能量桩整体的换热性能。相比之下,0°锥角下的高温流体流过更多的螺旋圈数,几乎到达了能量桩的中部,导致换热效果较差。
图8所示为不同锥角条件下的纵向对称面的温度分布云图。从图中可以看出,圆台型螺旋能量桩的底部热干扰现象较为严重,且锥角越大,底部热干扰越明显。这是因为圆台型螺旋能量桩底部的螺旋半径较小,由于热量的积聚,在经向和轴向都存在热短路现象。相反,由于顶部螺旋半径较大,热干扰效应较弱。另外从图中可以明显看出,随着锥角的增大,轴向相邻管段间的土壤高温区域明显减小,这是因为在相同深度方向螺距()的条件下,锥角越大,轴向相邻管段间的距离()越大,可以有效地减少轴向热干扰。

图7 管壁温度分布
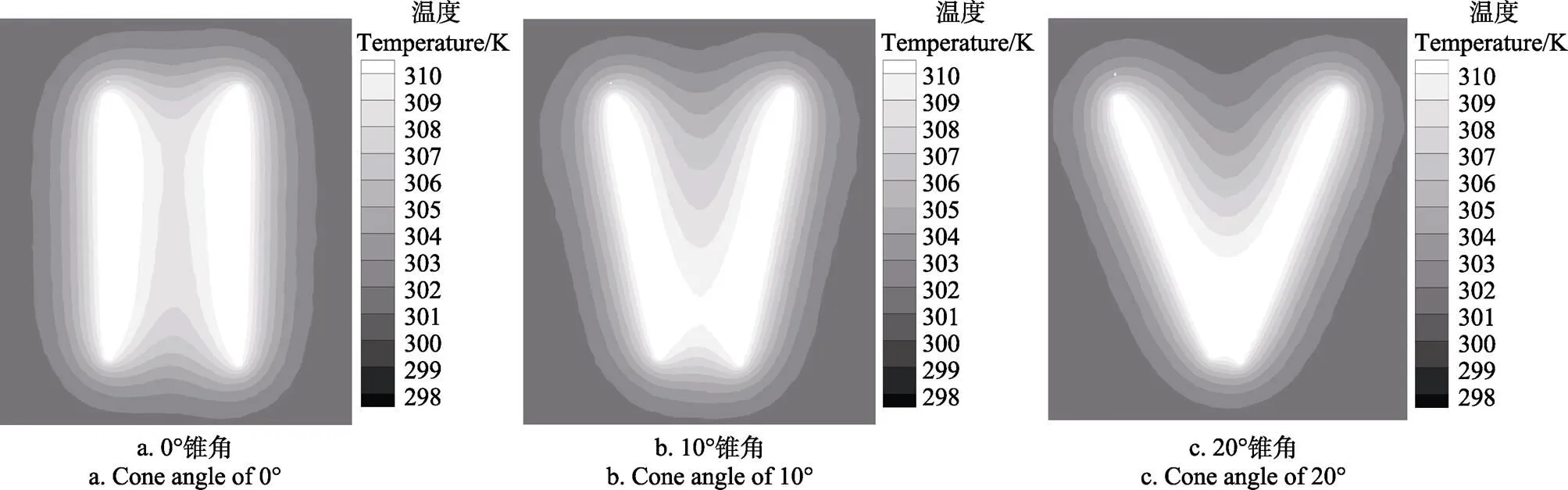
图8 纵向对称面的温度分布
4 结 论
为了减少热干扰、提高换热效率,提出了一种新型“圆台型螺旋能量桩(truncated cone helix energy pile,CoHEP)”。同时为了更加准确地模拟研究新型圆台型螺旋能量桩的换热特性,本文综合考虑初始土壤温度的不均匀性和土壤上表面动态边界条件,利用数值模拟的方法分析研究了不同锥角下圆台型螺旋能量桩的换热特性。通过分析得到如下结论:
1)圆台型螺旋能量桩沿水流方向可以分为四个换热阶段:入口阶段→热短路阶段→小温差阶段→出口阶段。入口阶段的换热能力最强,在热短路阶段和小温差阶段换热能力持续下降,出口阶段有所回升。
2)圆台型螺旋能量桩的底部热干扰现象较为严重,且锥角越大,底部热干扰越明显。相反,由于顶部螺旋半径较大,热干扰效应较弱。此外,锥角越大,在相同深度方向螺距()的条件下,轴向相邻管段间的距离()越大,轴向热干扰作用越小。
3)在相同的管长(L)、深度方向螺距()和能量桩高度(h)的情况下,增大锥角将增大能量桩顶部螺旋半径(r),导致能量桩上部热干扰作用减小,同时使更多的高温流体位于能量桩上部,和覆土区域直接接触,换热能力增大。此外,随着锥角的增大,轴向相邻管段间的距离增大,轴向热干扰作用减小。圆台型螺旋能量桩的单位管长换热量随着锥角的增大而线性增加,当系统运行时间为12 h时,锥角从0°增加到10°再增加到20°,单位管长换热量增长率分别为2.54%和3.53%。
4)新型圆台型螺旋能量桩上部的热干扰远小于传统圆柱型螺旋能量桩,且有更多的高温流体位于能量桩上部。此外,在深度方向螺距()相同的条件下,新型圆台型螺旋能量桩轴向相邻管段间的距离()明显大于传统圆柱型螺旋能量桩,可有效降低轴向热干扰。因此,新型圆台型螺旋能量桩单位管长换热量大于传统圆柱型螺旋能量桩。且20°锥角条件下的单位管长换热量比传统圆柱型螺旋能量桩高了6.16%。
[1] Hamada Yasuhiro, Saitoh Hisashi, Nakamura Makoto, et al. Field performance of an energy pile system for space heating[J]. Energy and Buildings, 2007, 39(5): 517-524.
[2] Cecinato Francesco, Loveridge Fleur A. Influences on the thermal efficiency of energy piles[J]. Energy, 2015, 82: 1021-1033.
[3] Gao Jun, Zhang Xu, Liu Jun, et al. Thermal performance and ground temperature of vertical pile-foundation heat exchangers: A case study[J]. Applied Thermal Engineering, 2008, 28 (17-18): 2295-2304.
[4] Park Hyunku, Lee Seung-Rae, Yoon Seok, et al. Evaluation of thermal response and performance of PHC energy pile: Field experiments and numerical simulation[J]. Applied Energy, 2013, 103: 12-24.
[5] Zarrella Angelo, Capozza Antonio, De Carli Michele. Analysis of short helical and double U-tube borehole heat exchangers: A simulation-based comparison[J]. Applied Energy, 2013, 112: 358-370.
[6] Zarrella Angelo, De Carli Michele. Heat transfer analysis of short helical borehole heat exchangers[J]. Applied Energy, 2013, 102: 1477-1491.
[7] Zarrella Angelo, De Carli Michele, Galgaro Antonio. Thermal performance of two types of energy foundation pile: Helical pipe and triple U-tube[J]. Applied Thermal Engineering, 2013, 61(2): 301-310.
[8] Man Yi, Yang Hongxing, Diao Nairen, et al. A new model and analytical solutions for borehole and pile ground heat exchangers[J]. International Journal of Heat and Mass Transfer, 2010, 53(13-14): 2593-2601.
[9] Zhang Wenke, Yang Hongxing, Lu Lin, et al. Investigation on heat transfer around buried coils of pile foundation heat exchangers for ground-coupled heat pump applications[J]. International Journal of Heat and Mass Transfer, 2012, 55 (21): 6023-6031.
[10] Wang Deqi, Lu Lin, Cui Ping. A novel composite-medium solution for pile geothermal heat exchangers with spiral coils[J]. International Journal of Heat and Mass Transfer, 2016, 93: 760-769.
[11] Li Min, Lai Alvin C. K. Heat-source solutions to heat conduction in anisotropic media with application to pile and borehole ground heat exchangers[J]. Applied Energy, 2012, 96: 451-458.
[12] Zhang Wenke, Yang Hongxing, Lu Lin, et al. The research on ring-coil heat transfer models of pile foundation ground heat exchangers in the case of groundwater seepage[J]. Energy and Buildings, 2014, 71: 115-128.
[13] Zhang Wenke, Yang Hongxing, Lu Lin, et al. The analysis on solid cylindrical heat source model of foundation pile ground heat exchangers with groundwater flow[J]. Energy, 2013, 55: 417-425.
[14] Bezyan Behrad, Porkhial Soheil, Mehrizi Abbasali Aboui. 3-D simulation of heat transfer rate in geothermal pile- foundation heat exchangers with spiral pipe configuration[J]. Applied Thermal Engineering, 2015, 87: 655-668.
[15] Jalaluddin, Akio Miyara. Thermal performance and pressure drop of spiral-tube ground heat exchangers for ground-source heat pump[J]. Applied Thermal Engineering, 2015, 90: 630-637.
[16] Xiang Yong, Su Hua, Gou Wenshi, et al. A new practical numerical model for the energy pile with spiral coils[J]. International Journal of Heat and Mass Transfer, 2015, 91: 777-784.
[17] Ghasemi-Fare Omid, Basu Prasenjit. A practical heat transfer model for geothermal piles[J]. Energy and Buildings, 2013, 66: 470-479.
[18] Li Huai, Nagano Katsunori, Lai Yuanxiang. A new model and solutions for a spiral heat exchanger and its experimental validation[J]. International Journal of Heat and Mass Transfer, 2012, 55(15-16): 4404-4414.
[19] Loveridge Fleur, Powrie William. Temperature response functions (G-functions) for single pile heat exchangers[J]. Energy, 2013, 57: 554-564.
[20] Loveridge Fleur, Powrie William. G-Functions for multiple interacting pile heat exchangers[J]. Energy, 2014, 64: 747-757.
[21] Park Sangwoo, Lee Dongseop, Choi Hyun-Jun, et al. Relative constructability and thermal performance of cast-in-place concrete energy pile: Coil-type GHEX (ground heat exchanger) [J]. Energy, 2015, 81: 56-66.
[22] Park Sangwoo, Sung Chihun, Jung Kyoungsik, et al. Constructability and heat exchange efficiency of large diameter cast-in-place energy piles with various configurations of heat exchange pipe[J]. Applied Thermal Engineering, 2015, 90: 1061-1071.
[23] Yang Weibo, Lu Pengfei, Chen Yongping. Laboratory investigations of the thermal performance of an energy pile with spiral coil ground heat exchanger[J]. Energy and Buildings, 2016, 128: 491-502.
[24] Huang Guangqin, Yang Xiaofeng, Liu Yajiao, et al. A novel truncated cone helix energy pile: Modelling and investigations of thermal performance[J]. Energy and Buildings, 2018, 158: 1241-1256.
[25] 余延顺,张少凡,马娟,等. 土壤耦合热泵系统模型试验台设计[J]. 南京理工大学学报(自然科学版),2010,34(5):613-617. Yu Yanshun, Zhang Shaofan, Ma Juan, et al. Design of scale-model experiment platform for ground-coupled heat pump system[J]. Journal of Nanjing University of Science and Technology (Natural Science), 2010, 34(5): 613-617. (in Chinese with English abstract)
[26] CECS 344: 2013,地源热泵系统地埋管换热器施工技术规程[S].
[27] 孔磊. 螺旋型地埋管换热器换热性能的研究[D]. 扬州:扬州大学,2015. Kong Lei. Study on Heat Transfer Performance of Helix Buried Heat Exchanger[D]. Yangzhou: Yangzhou University, 2015.
[28] Lim Kyoungbin, Lee Sanghoon, Lee Changhee. An experimental study on the thermal performance of ground heat exchanger[J]. Experimental Thermal and Fluid Science, 2007, 31(8): 985-990.
[29] Luo Jin, Rohn Joachim, Xiang Wei, et al. Experimental investigation of a borehole field by enhanced geothermal response test and numerical analysis of performance of the borehole heat exchangers[J]. Energy, 2015, 84: 473-484.
[30] Vashistha Chaitanya, Patil Anil Kumar, Kumar Manoj. Experimental investigation of heat transfer and pressure drop in a circular tube with multiple inserts[J]. Applied Thermal Engineering, 2016, 96: 117-129.
[31] William L. Oberkampf, Timothy G. Trucano. Verification and validation in computational fluid dynamics[J]. Progress in Aerospace Sciences, 2002, 38(3): 209—272.
[32] CJJ-101, 埋地聚乙烯给水管道工程技术规程[S].
Simulation analysis and verification of heat transfer characteristics of truncated cone helix energy pile
Liu Yajiao1, Huang Guangqin1※, Lu Jun2, Yang Xiaofeng1, Zhuang Chunlong1
(1.401311,; 2.400045,)
In order to reduce the thermal interference and to improve the heat transfer efficiency, a novel “truncated cone helix energy pile (CoHEP)” was proposed in this study. And in order to simulate the thermal performance of the novel CoHEP more accurately, a three-dimensional numerical model was established with consideration of the inhomogeneous initial soil temperature and the dynamic boundary condition above the soil surface. The heat transfer characteristic of the novel CoHEP of different cone angles was studied. In addition, in order to verify the accuracy of the numerical model, a verification test was conducted. The results showed that the novel CoHEP can be divided into four heat transfer stages along the flow direction: entrance stage → thermal short circuit stage → small temperature difference stage → exit stage. Among them, the heat transfer capacity of the entrance stage was the strongest, and the heat transfer capacity continued to decrease during the thermal short circuit stage and the small temperature difference stage, eventually the heat transfer capacity rebounded during the exit stage. The thermal interference at the bottom of the CoHEP was more serious, and the larger the cone angle, the more serious the thermal interference at the bottom. In contrast, the thermal interference effect was weaker at the top of the CoHEP due to the larger helix radius at the top. The heat flux per unit pipe length of the CoHEP increased linearly with the increase of cone angle. That was because with the same pipe length (L), pitch in the depth direction () and energy pile height (h), increasing the cone angle would increase the top radius (r) of the CoHEP, leading to small thermal interference in the upper part of the CoHEP. At the same time, more high-temperature fluid was located in the upper part of the CoHEP which directly contacted with the covered soil area. Thus the heat transfer capacity increased. When the system operating time was 12 h, the cone angle increased from 0°to 10°to 20°, the increasing rate of the heat flux was 2.54% and 3.53%, respectively. The thermal interference in the upper part of the novel CoHEP was much smaller than that of the traditional CyHEP, and more high-temperature fluid was located in the upper part of the energy pile which was good for heat transfer. In addition, the distance between the adjacent pipes in the axial direction () of the novel CoHEP was significantly larger than that of the traditional CyHEP under the same pitch in the depth direction (), which can effectively reduce the axial thermal interference. Thus the heat flux per unit pipe length of the novel CoHEP was greater than the traditional CyHEP. And when the cone angle was 20°, the heat flux per unit pipe length of the novel CoHEP was 6.16% higher than that of the traditional CyHEP.
heat pump system; heat transfer; numerical simulation; helix energy pile
刘亚姣,黄光勤,卢 军,杨小凤,庄春龙.圆台型螺旋能量桩换热特性的模拟分析与验证 [J]. 农业工程学报,2018,34(7):227-234. doi:10.11975/j.issn.1002-6819.2018.07.029 http://www.tcsae.org
Liu Yajiao, Huang Guangqin, Lu Jun, Yang Xiaofeng, Zhuang Chunlong. Simulation analysis and verification of heat transfer characteristics of truncated cone helix energy pile[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 227-234. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2018.07.029 http://www.tcsae.org
2017-12-05
2018-02-26
国家自然科学基金项目(51706243);国家自然科学基金项目(51478058);重庆市基础科学与前沿技术研究项目(cstc2016jcyjA0496)
刘亚姣,男,河南舞阳人,博士,主要从事建筑节能与浅层地热能利用方面的研究。Email:lyj199164@126.com
黄光勤,男,重庆人,博士、讲师,主要从事建筑节能与浅层地热能利用方面的研究。Email:hgq880818@163.com
10.11975/j.issn.1002-6819.2018.07.029
TK124
A
1002-6819(2018)-07-0227-08
