单壁碳纳米管热导率几个问题的定量描述与分析
2015-12-05蒋玲芳赵俊红
刘 煜,蒋玲芳,赵俊红
(1.河南省电力公司 电力科学研究院,河南 郑州 450052;2.中国民航飞行学院 洛阳分院,河南 洛阳 471000)
热导率(κ)是单壁碳纳米管的重要物性参数之一,该参数的研究受到广泛关注.由于实验技术的困难,通过实验获得的热导率的数据不多[1-4],且尚无一致认可的实验结果,更未能进行多个影响因素、多种条件下的实验研究.因此,理论分析和分子动力学模拟就成为热导率研究的重要手段.热导率的影响因素有温度、管长、管径、手性、缺陷等[5-10].文献[5]借助声子色散关系研究了热导率随温度的变化;文献[6]通过求解线性Boltzmann-Peierls声子输运方程,讨论了热导率与管长的关系;文献[7-10]通过分子动力学模拟分别研究了温度、管长、管径对碳纳米管热导率的影响;运用非平衡分子动力学方法,文献[11]研究了碳管中的点缺陷对热导率的影响.上述这些研究从不同侧面和不同角度丰富了人们对碳纳米管热导率的认识.
在现有文献中,关于热导率-温度关系曲线在什么条件下能够达到峰值存在几种不同的看法[1,12-13],并且这些看法都是定性分析,未给出定量的计算结果和分析论证.热导率κ会随管长L的增加而增大[9-10],但目前用来描述热导率的管长依赖性的指数关系式κ=aLα(指数α>0)[6,9,14],由于热导率κ随管长L的增加而发散,被认为是不太合理的.如果考虑二阶或高阶三声子过程,热导率随管长的增加最终应当趋于有限值[6,15],不过目前还没有可以恰当描述热导率随管长的增加最终趋于有限值的数学表达式.虽然文献[14]试图对指数关系式进行修正,但结果不很理想.声子的平均自由程l是影响热导率的主要因素之一,但通过数学关系式表达和分析平均自由程随温度和管长变化,以及平均自由程与输运方式关系的文献却极少.文献[16]发现,在极低温度(T<30K)下热导率与温度成线性关系,通过热导率的基本关系式κ=cv·v·l/3(其中,cv为单位体积比热,v为声子群速度)可建立单壁碳纳米管束的热导率与温度和声子平均自由程的函数关系,不过该函数关系只适合于估算极低温度下声子的平均自由程.
为了定量分析和讨论上述问题,作者利用文献[6,14,17-18]中给出的碳纳米管热导率和比热数据,通过拟合的方法分别建立起数学关系式,并利用这些关系式定量讨论κ随T和L的变化,研究κ-T关系曲线达到峰值应当满足的条件以及影响峰值位置的因素;提出不同于指数函数的描述热导率的管长依赖性数学表达式,利用该式描述热导率随管长的增加最终趋于有限值的情形;还定量分析声子平均自由程l随T和L的变化,探讨κ随L的增加趋于有限值的原因.
1 定量关系式的建立
根据声子气模型和晶格动力学理论,计算晶格热导率的公式为
其中:κ为热导率;cv为单位体积比热;v为声子的群速度;l为声子的平均自由程.
对于准一维的碳纳米管,式(1)中的系数1/3应当去掉[2,14,19],因此,碳纳米管的热导率可由下式计算
其中:v对温度不敏感,而cv和l则对温度非常敏感,二者都是温度的函数.
理论研究表明[4-5,7-8],热导率κ在低温段会随温度T升高而升高,在高温段随温度T升高而下降,κ-T关系曲线存在峰值.该文假设热导率κ与温度T具有如下函数关系
其中:a、b为待定参数,可通过数据拟合确定.
文献[14,17]利用分子动力学模拟得到了(5,5)单壁碳纳米管的热导率随温度和管长变化的数据.文献[6]通过求解线性Boltzmann-Peierls声子输运方程,计算了不同温度和管长条件下(10,0)单壁碳纳米管的热导率.(5,5)和(10,0)两种碳管虽然手性不同,但管径比较接近,R(5,5)=0.34nm,R(10,0)=0.39nm.考虑到直径相同时,手性角对碳管热导率影响不大,因此两种碳管的热导率数据具有一定的可比性[14].
作者利用文献[6,14,17]的数据,通过不同温度和管长条件下热导率数据的拟合,得到参数b=0.003 1.参数a是管长L的函数,对不同管长时的a值进行拟合,得到a=5.86(L/(L+94)).将参数a和b的具体形式(或数值)代入式(3),得到热导率κ与管长L和温度T的关系式为
图1为利用式(4)计算得到的温度T=300K时热导率κ随管长L变化的曲线,计算值与有关文献[14,17]的结果基本吻合,因此可以利用式(4)进行计算分析.
比热是影响热导率的重要因素之一.文献[18]讨论了单壁碳纳米管的比热性质,给出了基于声子谱的(10,10)碳管比热与温度的理论关系曲线(见图2).为了方便后面的计算分析,作者利用该曲线的数据,拟合得到比热cv随温度T变化的关系式
其中:kB为Boltzmann常数,M0为碳原子的质量.
图2给出了(10,10)单壁碳纳米管的比热cv随温度T变化的理论曲线和拟合曲线.由图2可见,拟合曲线与理论曲线基本吻合.碳管的直径对比热有一定影响[18],但影响很小,可以忽略不计,因此在后面的计算分析中可以直接使用式(5).
在式(5)中引入碳纳米管的密度值ρ,可得单位体积比热
其中:ρ可近似取为1.28×106g·m-3[20].
将式(4)、(6)代入式(2),可得声子平均自由程l与管长L和温度T的函数关系为
根据文献[9]给出的(5,5)碳纳米管的声学声子模式(包括横波、纵波和卷曲模式)的群速度进行计算,得到v≈10×103m·s-1.
2 结果和讨论
在本节里,将利用前面建立的几个数学关系式,以完整无缺陷的单个(5,5)单壁碳纳米管为例,对与热导率有关的几个问题进行讨论.
2.1 温度和管长对κ的影响
利用式(4)绘制了热导率κ与温度T和管长L的关系曲线图,如图3所示.由图3可见,管长一定时,热导率随温度升高而提高,在300~400K时达到峰值;温度继续升高时,热导率下降;温度越高,κ越小,即κ∝1/T;当温度一定时,管长L越长,热导率越大.可见式(4)可以较好地描述温度T和管长L两个因素对碳纳米管热导率的影响.
对于κ-T曲线的峰值位置,有些文献给出的数值为85~100K[7,12],有些则在300~400K[4,8,11],至今尚无定论.已有的研究表明,碳管的手性和管径会影响峰值位置:对于锯齿型碳管,峰值位置随着碳管直径的增大向低温区移动[12];对于扶手椅型碳管,峰值位置随着碳管直径的增大向高温区移动[8],导致移动的机制目前尚不十分清楚.对式(4)求κ对T的一阶偏导数并令其等于零,可求得κ出现峰值的温度为322.6K,这与文献[4,8,11]的结果接近,并且峰值位置与管长L无关.
关于κ在什么条件下达到峰值,目前尚无一致的观点.有关文献[1,12-13]均为定性分析,未用定量的计算结果来予以证明.作者利用式(7)对κ达到峰值所需满足的条件作如下计算分析.
在低温条件下,U散射被“冻结”,可以假设T=25K时的声子平均自由程l等于静态长度lst,即lst=l(T=25K).利用式(7)计算声子平均自由程l,然后利用关系式计算 U 散射长度lum.图4为不同管长L条件下U散射长度lum随温度T的变化.图4表明,在所有给定的管长条件下,U散射长度lum都随温度的升高而下降.
表1给出了不同管长和温度下声子的静态长度lst和U散射长度lum.由表1可知,lum随温度升高而下降,在T=300K和T=350K时,lum与lst最为接近,根据文献[1]的观点,峰值位置应该在T=300~350K之间,而前文给出的峰值位置的解析数值T=322.6K就处在这一温度范围内.上述定量计算结果表明,lum≈lst可以作为κ达到峰值的条件,这也证实了文献[1]的假设是有道理的,对单壁碳纳米管也同样适用.
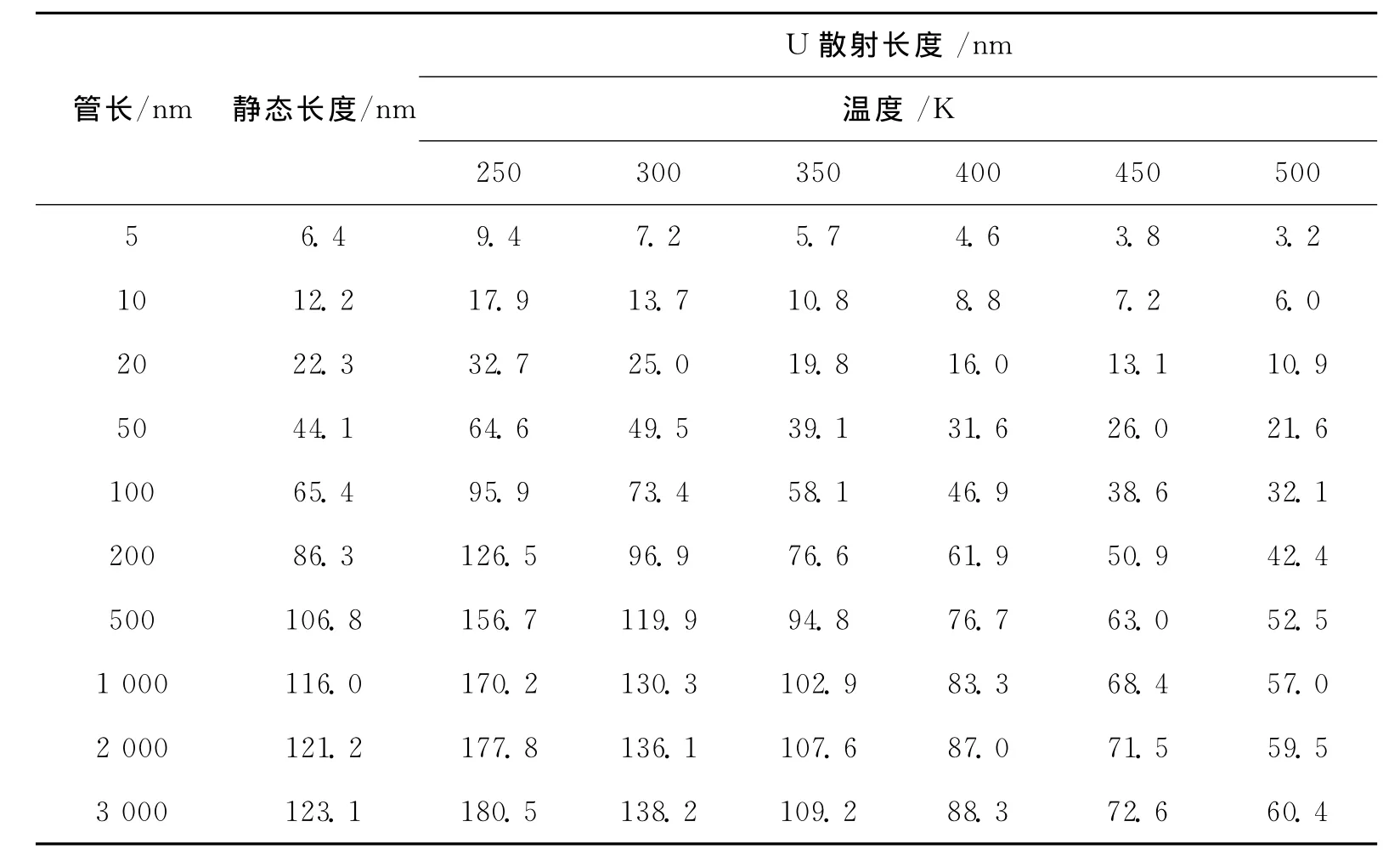
表1 不同管长和温度下声子的静态长度和U散射长度Tab.1 The static length and U scattering length of phonon at different temperatures and lengths
表2给出了峰值温度322.6K时的声子平均自由程l和U散射长度lum的数据.由表2可知,对各个管长,l约为lum的一半.因此,关于κ达到峰值的条件,还可以得到如下观点:当声子平均自由程l等于U散射长度lum的一半时,κ达到峰值.
从理论上讲,峰值位置需要严格满足的条件可由式(2)得到.对式(2)求κ对T的一阶导数,得
当κ达到峰值时,有dκ/dT=0.满足dκ/dT=0的条件为
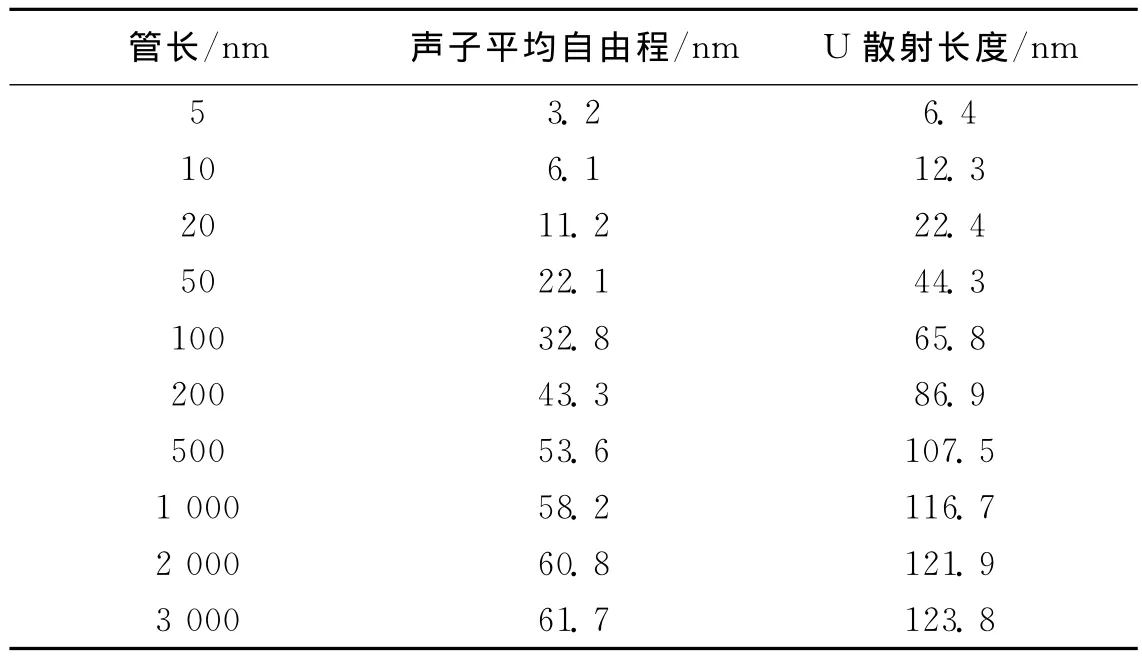
表2 峰值温度(T=322.6K)下的声子平均自由程和U散射长度Tab.2 The phonon mean free path and U scattering lengths at the peak temperature(T=322.6K)
利用式(6)~(7)计算峰值温度T0=322.6K时式(9)中的各个参数,得这些数据能满足式(11).
这一定量计算结果表明,峰值位置不仅取决于cv和l的数值大小,还与二者随温度的变化率密切相关,因此在分析κ达到峰值所需满足的条件时,必须把二者随温度的变化率考虑在内.
2.2 κ的管长依赖性及其数学表达
对于碳管热导率的管长依赖性,众多文献[6,9,14-15,21]采用理论、实验和分子动力学模拟进行了研究.结果表明,热导率随管长的增加而增大,二者具有指数关系κ∝Lα.这种指数关系造成热导率随管长的增加而发散,而这种发散的结果被认为是不合理的.如果考虑二阶或高阶三声子过程,热导率随管长的增加最终应当趋于有限值[6,15].文献[14]研究发现,指数关系式κ=κ0Lα中的指数α会随着L的增大而降低,并且通过数据拟合得出α=2.38L-0.34,因此存在关系式.这一关系式避免了发散的结果.不过,用该式描述κ随L的变化时,κ不是随L的增加而单调增大直至收敛,而是随L的增加先是增大,在L=18.93时出现极大值(可由dκ/dL=0求得),然后κ随L的增大逐渐减少,最终收敛于κ0.因此,该关系式也未能合理反映热导率随管长的增加最终趋于有限值的结果.
上述研究表明,热导率会随着管长增加而增大,但是用指数函数来描述二者的函数关系,不能恰当描述收敛的结果.部分文献采用指数函数的形式来描述κ与L的关系是因为:在热力学极限下,一维原子链的κ与L成指数关系κ=κ0Lα[14],将这一关系用于具有准1维结构的碳纳米管是很自然的.但严格来说,碳纳米管具有3维空间结构,其原子可在3维空间运动,把适用于1维结构的理论和公式用于具有3维结构的体系,容易造成不合理的结果.
作者利用式(4)计算了不同温度下热导率随管长的变化,结果见图5.由图5可见,热导率随着管长增加而增大,当管长大于100nm后,热导率随着管长增大的幅度逐渐减小,随着管长进一步增加,热导率逐渐趋于有限值.这一结果,与文献[6]在考虑二阶或高阶三声子过程后,热导率随管长的增加而增大并最终趋于有限值的结果是一致的.
将式(4)改写为
其中:κ0=5.86Te-0.0031T.求κ对L的一阶导数,得
由式(10)~(11)可知,∂κ/∂L>0,κ与L的关系曲线没有峰值.当L→∞,∂κ/∂L→0,κ→κ0.因此,将κ与L的函数关系表示成式(10)的形式,可以避免出现发散的结果,并且可以描述κ随L增加而增大,最终趋于有限值的情形,该有限值即κ0,它只与温度有关.这意味着当管长L足够大时,κ仅是温度T的函数.
2.3 声子的平均自由程及声子的输运
作者利用式(7)计算了不同温度和管长条件下的声子平均自由程l,结果见图6.由图6可见,l随温度T的升高而下降;温度T一定时,l随管长L的增加而增大.
图7a为声子平均自由程l与管长L的关系曲线,图中对角线表示l=L.由图7a可见,温度一定时,l随管长L增加而增大,当L大于100nm后,l随L增大的幅度逐步减小,并且最终趋于有限值.由图7a还可以看出,在低温(如25、100K)条件下,随着管长增加,声子平均自由程l从大于管长L转变为小于管长;当管长较短(如L=10nm)时,随着温度升高,声子平均自由程l也从大于管长L转变为小于管长.
图7b给出了不同温度下声子平均自由程l与管长L的相对长度(l/L)随L的变化情况.由图7b可见,温度一定时,管长L增加会使l/L迅速下降;管长一定时,温度越高,l/L越小.管长或温度改变会使声子平均自由程l从大于管长L(l/L>1)转变为小于管长(l/L<1).当温度较高或管长较长时,会出现l/L≪1的情形.一般来说,当声子平均自由程大于体系的尺度时,声子表现为弹道输运;当声子平均自由程与体系的尺度相当时,声子表现为弹道-扩散输运;当声子平均自由程远小于体系的尺度时,声子表现为扩散输运[14,21].因此,当温度或管长改变,使得声子平均自由程从大于管长转变为小于管长时,声子的输运方式也会随之改变.可用l与L的比值l/L作为表征声子输运方式的参数,当l/L>1时,声子表现为弹道输运;当l/L≤1时,声子的输运为弹道-扩散输运,l/L越小,扩散输运所占比重越大;当l/L≪1(或l/L→0)时,声子的输运为扩散输运.从声子输运的角度来看热导率随管长的增加最终趋于有限值的现象,可以认为:随管长L增加,声子平均自由程l趋于有限值,必然会使比值l/L→0,此时声子的输运近似为完全的扩散输运.由于声子扩散输运时热导率κ不随L变化[14],所以κ将不随管长增加而增大,而将趋于有限值.
3 结束语
(1)该文得出的定量关系式可以较好地描述温度T和管长L对热导率κ的影响,κ随L变化的关系式也可以合理地描述κ随L的增加而增大,最终趋于有限值的情形.
(2)κ-T关系曲线的峰值位置与cv和l的数值及二者随温度的变化率有关而与管长L无关;当声子平均自由程l等于U散射长度lum的一半时,κ达到峰值.
(3)温度一定时,声子平均自由程l随管长L增加而增大,但增大的幅度逐步减小,并最终趋于有限值.
(4)声子的输运方式会随温度和管长变化而变化.温度或管长改变时,声子平均自由程l从大于管长L转变为小于管长,声子的输运从弹道输运转变为弹道-扩散输运;l与L的比值l/L越小,扩散输运所占比重越大,热导率随管长增加的幅度越小;当l/L→0时,声子的输运为扩散输运,热导率不再随管长的增加而增大.
(5)该文提出的关系式和分析结果适用于完整无缺陷的单个单壁碳纳米管.
[1]Kim P,Shi L,Majumdar A,et al.Thermal transport measurements of individual multi-walled carbon nanotubes[J].Physical Review Letters,2001,87(21):215502.
[2]Yu C,Shi L,Yao Z,et al.Thermal conductance and thermopower of an individual single-wall carbon nanotube[J].Nano Letters,2005,5(9):1842-1846.
[3]Fujii M,Zhang X,Xie H Q,et al.Measuring thermal conductivity of single carbon nanotube[J].Physical Review Letters,2005,95(6):065502.
[4]Pop E,Mann D,Wang Q,et al.Thermal conductance of an individual single-wall carbon nanotube above room temperature[J].Nano Letters,2006,6(1):96-100.
[5]Gu Y F,Chen Y F.Thermal conductivity of single-walled carbon nanotubes calculated from the complete phonon dispersion relation[J].Physical Review B,2007,76(13):134110.
[6]Mingo N,Broido D A.Length dependence of carbon nanotube thermal conductivity and the“problem of long waves”[J].Nano Letters,2005,5(7):1221-1225.
[7]Berber S,Kwon Y K,Toma′nek D.Unusally high thermal conductivity of carbon nanotubes[J].Physical Review Letters,2000,84(20):4613-4616.
[8]Osman M A,Srivastava D.Temperature dependence of thermal conductivity of individual single-wall carbon nanotubes[J].Nanotechnology,2001,12:21-24.
[9]Maruyama S.A molecular dynamics simulation of heat condition in finite length SWNTs[J].Physica B,2002,323:193-195.
[10]保文星,朱长纯.碳纳米管热传导的分子动力学模拟研究[J].物理学报,2006,55(7):3552-3557.
[11]李威,冯妍卉,陈阳,等.碳纳米管中点缺陷对热导率影响的正交试验模拟分析[J].物理学报,2012,61(13):136102.
[12]Cao J X,Yan X H,Xiao Y,et al.Thermal conductivity of zigzag single-walled carbon nanotubes:role of the umklapp process[J].Physical Review B,2004,69(7):073407.
[13]彭佳,冯妍卉,李威,等.含有Stone-Wales缺陷的碳纳米管的热导率模拟[J].工程热物理学报,2010,31(11):1901-1904.
[14]侯泉文,曹炳阳,过增元.碳纳米管的热导率:从弹道到扩散输运[J].物理学报,2009,58(11):7809-7815.
[15]王照亮,梁金国,唐大伟,等.单根单壁碳纳米管导热系数随长度变化尺度效应的实验和理论[J].物理学报,2008,57(6):3391-3396.
[16]Hone J,Whitney M,Piskoti C,et al.Thermal conductivity of single-walled carbon nanotubes[J].Physical Review B,1999,59(4):2514-2516.
[17]Shiomi J,Maruyama S.A molecular dynamics simulation of diffusive-ballistic heat condition in single-walled carbon nanotubes[J].Japanese Journal of Applied Physics,2008,47(4):2005-2009.
[18]吴延昭,谢宁,刘建静,等.单壁碳纳米管声子谱及比热计算[J].物理学报,2009,58(11):7787-7791.
[19]Wang Z L,Tang D W,Li X B,et al.Length-dependent thermal conductivity of an individual single-walled carbon nanotube[J].Applied Physics Letters,2007,91:23119.
[20]Dresselhaus M S,Eklund P C.Phonons in carbon nanotubes[J].Advances in Physics,2000,49(6):705-814.
[21]Wang J,Wang J S.Carbon nanotube thermal transport:ballistic to diffusive[J].Applied Physics Letters,2006,88:111909.
