基于改进4-方程摩擦模型的输水管道水锤压力计算

王振华，马习贺，李文昊，郑旭荣，张金珠



基于改进4-方程摩擦模型的输水管道水锤压力计算

王振华1,2※，马习贺1,2，李文昊1,2，郑旭荣1，张金珠1

（1. 石河子大学水利建筑工程学院，石河子 832000； 2. 现代节水灌溉兵团重点试验室，石河子 832000）

摩擦耦合是流体与管壁之间相对运动产生粘性摩擦力而形成的边界接触耦合。在流体高频运动的范围内，摩擦耦合的特性变得相对更加复杂，将直接影响管道系统的水锤演化。为了研究在实际管道中水锤的变化情况，本文基于Zielke模型对流固耦合作用（fluid-structure interaction，FSI）4-方程模型（four-equation model，4EM）建立的4-方程摩擦模型（four-equation friction model，4EFM）结合广义不可逆热力学理论（extended irreversible thermodynamics，EIT）进行改进，建立改进4-方程摩擦模型。通过MATLAB软件利用波速调整（wave-speed adjustment，WSA）插值方法的特征线法（method of characteristics，MOC），对新疆生产建设兵团第十三师自压输水管道中的关阀水锤压力进行数值计算，结果表明改进4-方程摩擦模型的计算结果相比4-方程摩擦模型以及其他计算模型与实测值具有更好的一致性，WSA相比其他线性插值方法可以减小插值误差。该改进模型可以应用在计算机中进行长距离重力流输水过程的水锤压力计算。

水锤；摩擦；耦合；特征线法；数值计算

0 引 言

管道输水是农田灌溉中高效节约、清洁环保的灌溉输水方式。但在管道系统充放水过程中，阀门的启闭或水泵机组启停等因素会诱发输流管道系统产生水锤。水锤是一种流体的非恒定流动，液体运动中所有空间点处的运动要素（流速、压强、加速度、切应力、密度等）都随着空间位置和时间的变化而改变。水锤问题是输流管道中常发生并且较难控制的问题，严重的水锤会导致管道部件的破裂以及爆管等事故。为保证管道系统的安全运行，众多专家学者结合实际工程对水锤的防护做了大量研究，比如防护设备的选用，阀门启闭方式以及启闭历时控制等措施[1-4]。但在防护措施实施之前需要对管道水锤的大小以及防护位置进行推算，目前大多数针对水锤计算的数值模型是基于恒定流摩阻项的一维水锤方程，忽略了管壁的切应力和对流项，对水锤压力波衰减过程和波形畸变难以做出准确的计算。

Zielke模型是1968年由Zielke针对层流问题提出的非稳态摩擦模型[5]。该模型考虑了与摩擦损失成正比的瞬时管壁剪切应力，将非恒定摩阻项同加权函数和历史加速度联系起来[6]。Adamkowsky和Lewandowsky验证了Zielke模型和其他一些非稳态摩擦模型，但没有考虑固定阀门的连接耦合问题[7]。4-方程模型（four-equation model, 4EM）是一组形式简单的线性偏微分方程组，描述了流固耦合作用（fluid-structure interaction, FSI）管道的轴向振动问题[8]。Lee[9]提出了描述输流管道非线性流固耦合运动的4-方程模型，建立了描述管道和液体的控制方程，但所得的偏微分方程不完全耦合，流固互动机制的描述不完整，并且忽略了输送高脉动频率流体时压力波对动力响应的影响。张立翔等[10-11]通过Hamilton变分原理和变形体内流体运动的微分方程建立管道-流体系统，得到了一个能反映管道内部流流固耦合、弯曲运动等因素对水锤特性影响的改进4-方程模型。杨超等[12-14]以经典4-方程为基础，依据Timoshenko梁理论，从对充液直管耦合振动的建模入手，得到了非恒定流充液管道的考虑摩擦耦合和泊松耦合的非线性的轴向振动4-方程模型。陈婷[15]等基于FSI处理得到用于计算耦合水锤的改进基本连续性方程，与简化后的流体动量方程、管道运动方程及物理方程构成了改进的轴向4-方程模型，将连续性方程中的水锤波速与流速的关系定义为能够反映耦合水锤特性的管道与流体在纵横两个方向均耦合的耦合波速，解决了4-方程模型在应用特征线法求解时，基本方程的建立和特征线定义不一致的情况。但Zielke模型和4-方程模型均难以提供水锤问题的精确求解方案，Ghodhbani A等[16]结合Zielke模型和4-方程模型在考虑摩擦耦合和连接耦合下提出了可以模拟简单管道中水锤变化的4-方程摩擦模型（four-equation friction model，4EFM），但该模型未对管壁剪切应力做出定义，未在工程实际中进行验证。本文结合Axworth等[17]从广义不可逆热力学理论（extended irreversible thermodynamics，EIT）推导出的一维非恒定管流的管壁切应力替换4-方程摩擦模型原有的管壁切应力计算方程，建立改进4-方程摩擦模型。该改进4-方程摩擦模型可以准确的反映非恒定摩阻项对于水锤波的影响。通过对新疆生产建设兵团第十三师自压输水管道进行末端关阀试验，对比分析了Zielke模型、4-方程模型、4-方程摩擦模型以及改进4-方程摩擦模型对管道水锤模拟的准确性以及波速调整（wave-speed adjustment，WSA）插值方法对水锤压力模拟精度的影响。

1 改进4-方程摩擦模型及求解

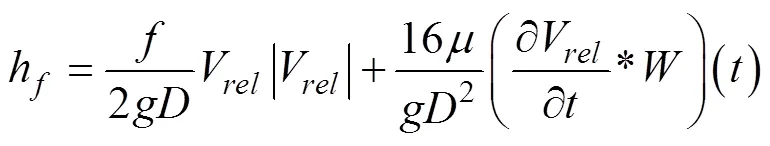
卷积关系展开式为：

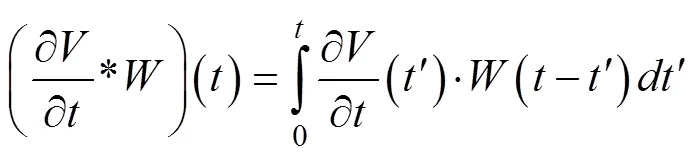
加权函数定义为：

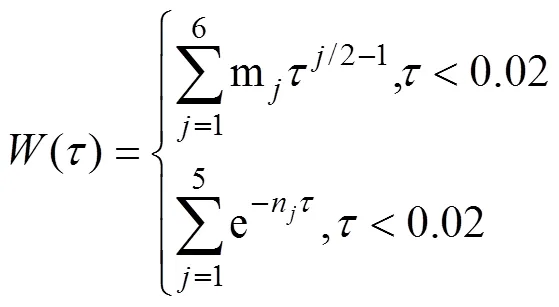
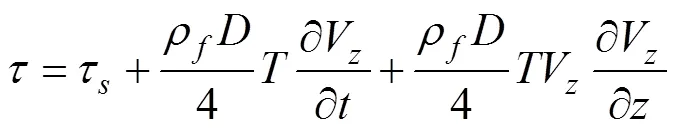
在充液满流管道系统中，所含的液体具有均匀性、各向同性和牛顿力学特性[20]，用Timoshenko理论和胡克定律对流体管道系统进行建模[21-23]，改进4EFM如下：

流体动量方程：

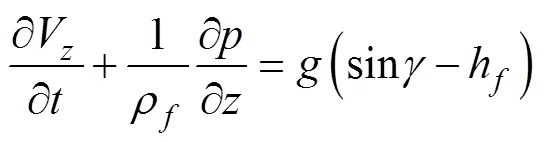
流体连续方程：

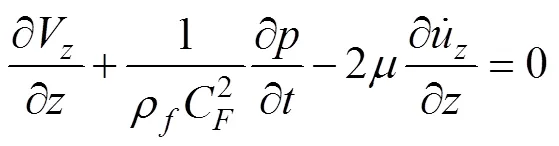
管道动力方程：

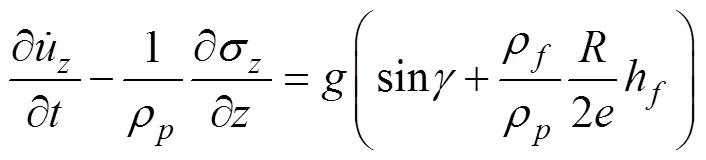
管道物理方程：

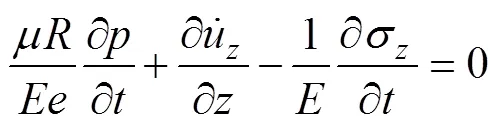
改进4EFM为双曲型偏微分方程，将式（5）～（8）耦合方程写成矩阵形式如下：

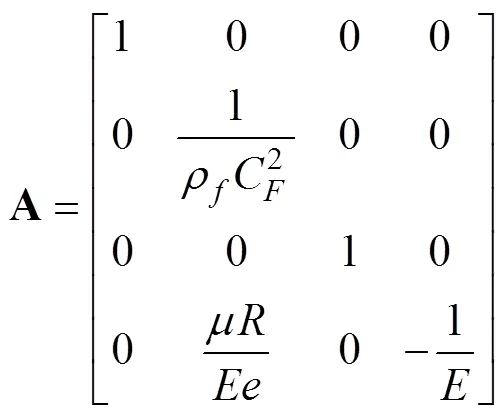
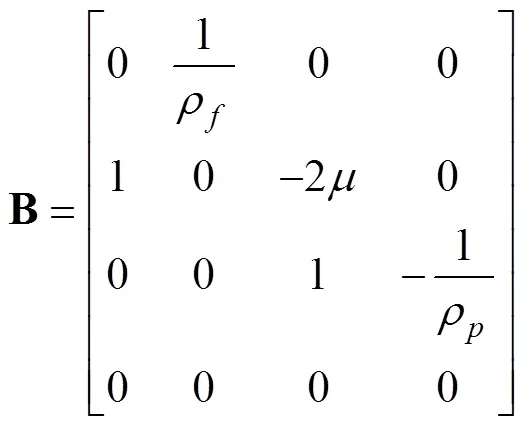
利用特征线法（method of characteristics，MOC）得到其特征方程为：

求解出相应的特征值：

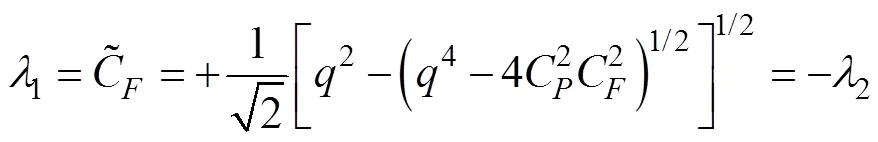
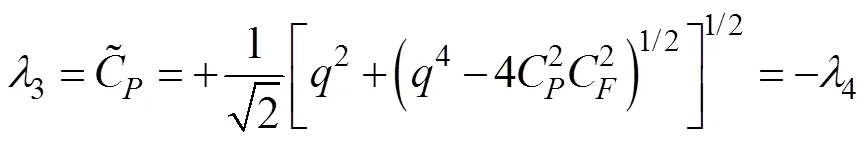
利用MOC进行瞬态数值计算[24-25]，其计算网格见图1，其中A1、A2、A3、A4为4条特征线，线上点为计算结点，p点为4条特征线交点。

为了进一步分析和验证改进4-方程摩擦模型对管道运动特性的影响，通过MOC推导以下相容性方程:

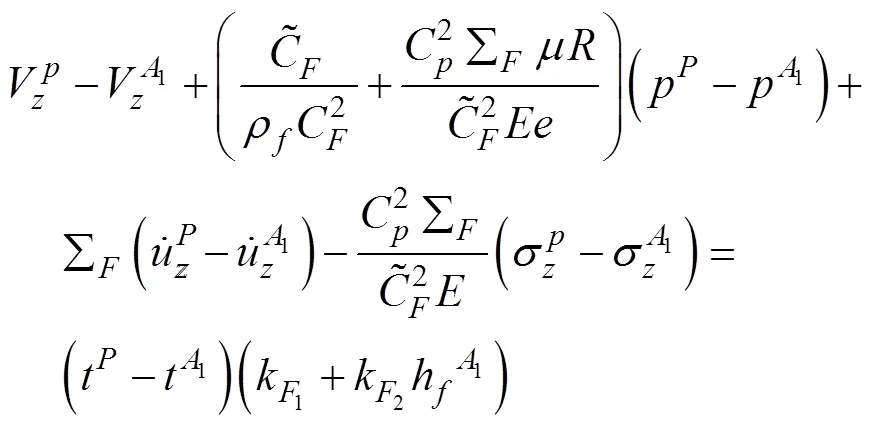
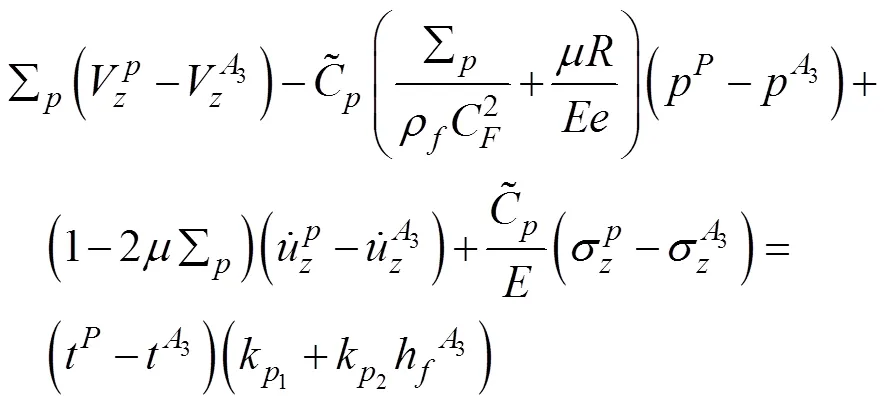
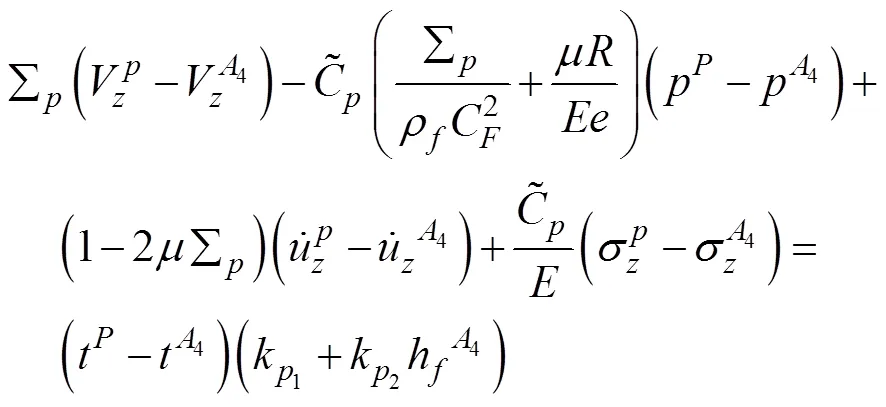
由于管道系统存在多种波，在使用特征线法计算时，需要通过插值方法来获取没有特征线通过的计算网格节点上的参数值，从而会产生插值误差。目前常用的有空间线性插值（space-line interpolation，SLI），时间线性插值（time-line interpolation，TLI）和波速调整（wave-speed adjustment，WSA）插值方法，Tijsseling[26]认为在计算水锤压力时WSA比线性插值更准确。为了便于在Matlab软件中计算，本文根据文献[27]提出以下矩阵公式：

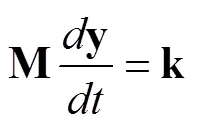
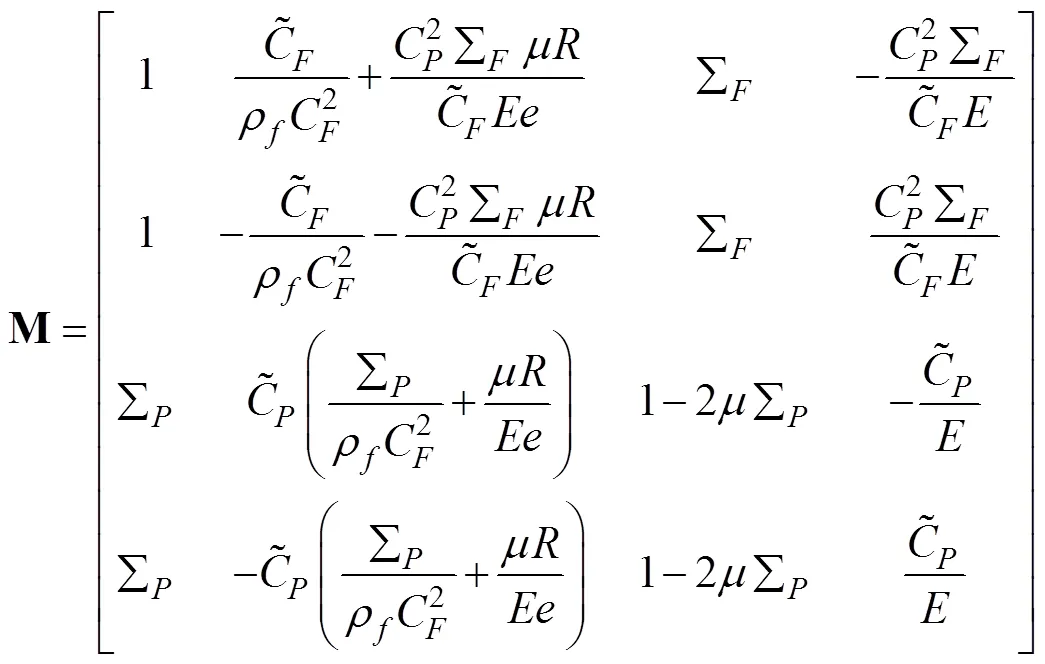
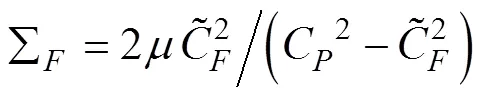
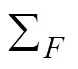
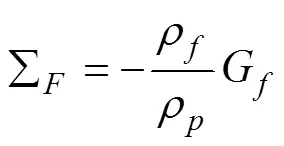
2 初始条件及边界条件

2.1 初始条件

初始条件根据稳定流计算，在瞬态流产生之前，假设输流管道系统处于平衡状态，根据式（5）～（8）推导的方程为：

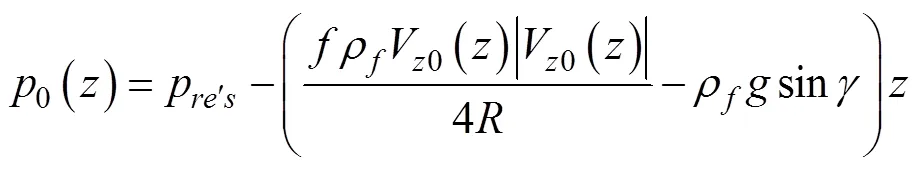
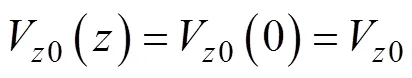
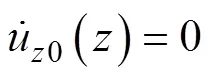
2.2 边界条件

构建如图2所示的水箱-管道-阀门简单管道系统，管道两端有水箱和阀门2个固定端。

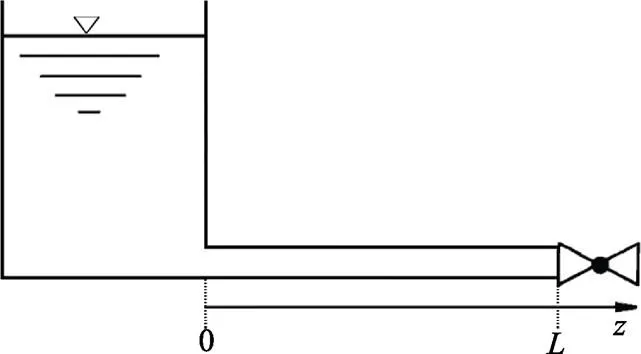
图2 水箱-管道-阀门简单管道系统

水箱压力恒定

固端约束

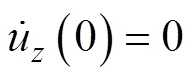
阀门处流体和管道同时运动

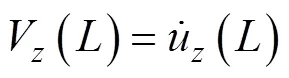
管道系统动态过程

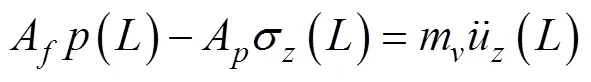
3 算例分析

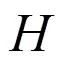
从图3可以看出各模型的水锤压力模拟计算值与实测值的初始压力均有上升趋势，水锤初始压力快速上升的原因与管道边界的变化方式有关[29]。Zielke模型计算出的初始压力升高值和实测值的第1个周期第1个压力上升值具有一致性（2=0.89），并且数据相近，相比4EM（2=0.79）、4EFM（2=0.83）和改进4EFM（2=0.85）可以较好的模拟出水锤压力的初期变化。但由于管道水锤压力波速的实测值与计算值之间的差异，Zielke模型和4EM在预测水锤变化趋势上与实测值具有较大误差，2模型分别在2 s和2.5 s时出现水锤压力衰减变化，相比实测值衰减提前1 s和0.5 s，从此出现了相位偏移，且随着时间的增大相位偏移量增大。Zielke模型在第4个周期之后出现与实测值相反的水锤压力波衰减变化情况，并且衰减速度加快，4EM计算的最大和最小水锤压力都与实测值相差较大，水锤压力振荡幅度大。4EFM（2=0.87）和改进4EFM（2=0.91）相比Zielke模型（2=0.79）和4EM（2=0.76）可以更加精确的模拟水锤发生瞬间的最大水锤压力升压值和降压值，并且能准确的描述第1个周期之后水锤压力波的畸变和衰减过程，同时改进4EFM相比4EFM的数值计算结果与实测值更具有良好的一致性，并且模拟相位偏移量不会随时间增加而逐渐增大，由此可以说明改进4EFM具有更佳的水锤压力计算效果。

图3 不同模型之间数值结果与实测值对比图

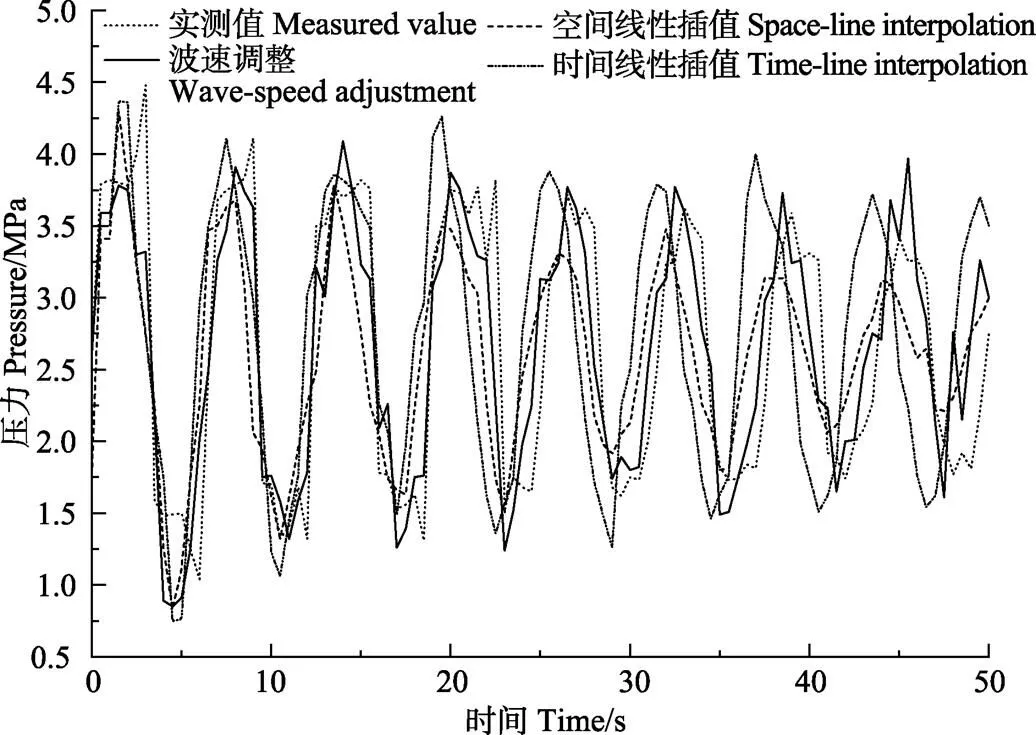
图4 不同插值方法对改进4EFM水锤压力计算的对比图

从图4计算得出，WSA、SLI和TLI的2值依次为0.83、0.79、0.76，WSA方法相比SLI和TLI对改进4EFM计算水锤压力的精度有所提升。在7.5 s时SLI和TLI插值计算的水锤压力值出现衰减，产生了相位偏移，并且相位偏移量随时间的延长而增大，TLI相比SLI所得到的水锤压力值具有更大的相位偏移以及数值振荡幅度。SLI所得水锤压力值振荡幅度较小，但其衰减速度快，水锤压力升高值远低于实测值。WSA插值计算的水锤压力和实测值具有较小的阻尼误差，出现相位偏移时间滞后，数值振荡较小，提高了改进4EFM计算水锤压力的稳定性和收敛性。

各计算模型与实测值以及使用不同插值方法的改进4EFM对水锤压力计算的定量分析如表1、表2所示。

表1 不同模型计算的水锤压力峰值相对误差分析

注：表1中1～8分别代表水锤压力波动第1～8个周期，水锤压力波动周期为前一个压力峰值到后一个压力峰值所经历的时间。下同。 Note：In Table 1~8 represents water hammer pressure fluctuation first to eighth cycle, respectively. The fluctuation period of water hammer pressure is the time of peak value of the previous pressure peak to the next pressure peak. The same bellow.

表2 改进4EFM在不同插值方法下水锤压力峰值相对误差分析

由表1可知：Zielke模型和4EM对于管道阀门处水锤压力峰值的捕捉效果不理想，Zielke模型在第1个周期相对误差高达15.63%，水锤压力峰值误差随着时间增加具有整体下降趋势，最低误差在第7个周期为1.39%。4EM在第1个周期相对误差达到8.04%，且误差随着时间增加而增大。4EFM和改进4EFM的阀门处水锤压力峰值捕捉误差都相对较小，4EFM在第3个周期水锤压力峰值误差较大，最高达到7.07%，误差多数大于3%，改进4EFM的最大误差出现在第1个周期为5.13%，并随着时间的增加误差振幅较小并无增大趋势，多数误差控制在1.5%以内，数值计算趋于稳定。

从表2可知：改进4EFM利用SLI方法计算的水锤压力峰值相对误差较大，多数在5%以上，并且具有继续增大的趋势，最高可达23.24%。TLI方法计算所得的水锤压力峰值在水锤压力波动前3周期相对误差较低，均小于3%，最低误差为0.24%，但从第4周期以后水锤压力峰值相对误差增大，并且基本高于WSA方法所计算的水锤压力峰值，WSA方法计算得的水锤压力峰值相对误差在第1周期以后都相对较小，因此WSA可以提高改进4EFM的水锤压力计算精度。

在水锤压力波传播过程中，近壁区在水锤压力波传到的同时先产生反向流动，而核心区由于流体惯性仍保持正向流动，由此在近壁区产生很大的瞬时流速梯度，进而产生较大的附加切应力和能量耗散，从而使水锤压力波的衰减速度加快[30]。Zielke模型和4EM中无法通过提高对摩阻项积分计算精度的方式妥善解决，4EFM考虑了附加摩阻项的影响，模拟精度将更加精确，而改进4EFM能够充分体现附加切应力的变化，因此能更加真实地反映管道中的水锤压力瞬变过程。

4 结 论

本文建立了改进4-方程摩擦模型（4EFM），通过MATLAB软件，使用波速调整（WSA）插值方法的特征线法（MOC）计算在关阀情况下简单管道中水锤的变化，并与实测值、Zielke模型、4EM和4EFM进行比较。结果表明：

1）在摩擦耦合以及连接耦合发生的情况下，Zielke模型和4EM都不适合计算管道水锤的变化，并且均具有严重的数值振荡和误差，2个模型相比实测值提前出现压力衰减变化，并出现相位偏移。改进4EFM和4EFM可以准确描述1个周期之后压力波的畸变和衰减过程，且模拟相位偏移量不会随时间增加而逐渐增大，契合度高。

2）改进4EFM相比4EFM在模拟效果上具有较大改善，各周期水锤压力峰值相对误差基本上小于1.5%，优于4EFM。在实际工程中，除客观试验条件影响外，改进4EFM计算的水锤压力值与试验数据具有较高的吻合度以及水锤波形、时间的契合度，能准确的捕捉长距离输水管道水锤压力的初期变化，水锤波衰减以及相位偏移等特征，可以进行长距离输水关阀水锤的模拟计算。

WSA方法相比SLI和TLI方法可以提高改进4EFM的水锤压力计算精度，提高水锤压力的预测能力。目前该改进4EFM在粘弹性管、多相流等环境下的水锤计算效果仍需要进一步的验证。

[1] 汪建平，杜燕子. 长距离有压输水工程水锤防护方案研究[J]. 供水技术，2015，9(6)：43－48.Wang Jianping, Du Yanzi .Water hammer control of long distance pressure water transmission pipeline[J].Water Technology, 2015, 9(6): 43－48. (in Chinese with English abstract)

[2] 虞之日，何丽俊，陈思良. 长距离管道有压自流输水工程末端阀门的选择[J]. 阀门，2012(2)：26－29.Yu Zhiri, He Lijun, Chen Siliang. Investigation on selection type of the outlet valve for long pipeline with gravity flow[J]. Valve, 2012(2): 26－29. (in Chinese with English abstract)

[3] 杨晓蕾，沈来新，俞锋，等. 重力流输水管道关阀水锤模拟研究[J]. 水利水电技术，2017，48(5)：95－96.Yang Xiaolei, Shen Laixin, Yu Feng, et al. Simulative study on water hammer from closing of valve of gravity flow water conveyance pipeline[J]. Water Resources and Hydropower Engineering, 2017, 48(5): 95－96. (in Chinese with English abstract)

[4] 罗浩，张健，蒋梦露，等. 长距离高落差重力流供水工程的关阀水锤[J]. 南水北调与水利科技，2016(1)：131－135.Luo Hao, Zhang Jian, Jiang Menglu, et al. Water hammer in the long-distance and high-drop water supply project of gravity flow[J]. South-to-North Water Transfers and Water Science & Technology, 2016(1):131－135. (in Chinese with English abstract)

[5] Zielke W. Frequency-dependent friction in transient pipe flow[J] .Journal of Basic Engineering, ASME , 1968, 90(1):109－115.

[6] 岑康，李长俊，廖柯熹，等. 液体管道瞬变流摩阻的计算方法[J]. 西南石油大学学报(自然科学版)，2005，27(3)：76－80. Cen Kang, Li Changjun, Liao Kexi, et al.Calculating methods of friction losses with transient flow in pipe [J].Journal of Southwest Petroleum University (Science &Technology Edition), 2005, 27(3): 76－80. (in Chinese with English abstract)

[7] Adamkowski A, Lewandowski M. Experimental Examination of Unsteady Friction Models for Transient Pipe Flow Simulation[J]. Journal of Fluids Engineering, 2006, 128(6): 1351－1363.

[8] 杨柯，李桂青. 充液管道流固耦合4-方程模型的一个解析解[J]. 水动力学研究与进展，1999(4)：493－503.Yang Ke, Li Guiqing. An Analytical Solution for Equations of Fluid-Structure Interaction in Liquid-filled Pipes[J].Journal of Hydrodynamics, 1999(4): 493－503. (in Chinese with English abstract)

[9] Lee U, Pak C H, Hong S C. The dynamics of a piping system with internal unsteady flow [J]. Journal of Sound and Vibration, 1995, 180: 297－311.

[10] 张立翔，杨柯，黄文虎. FSI效应对管道水击运动特性的影响分析[J]. 水电能源科学，2001，19(4)：43-47.Zhang Lixiang, Yang Ke, Huang Wenhu. Analysis of FSI effects on water hammer characteristics in piping flows[J]. International Journal Hydroelectric Energy, 2001, 19(4): 43－47. (in Chinese with English abstract)

[11] 张立翔，黄文虎. 输流管道非线性流固耦合振动的数学建模[J]. 水动力学研究与进展A辑，2000，15(1)：116－128. Zhang Lixiang, Huang Wenhu. Nonlinear Dynamical Modeling of Fluid-Structure Interaction of Fluid- Conveying Pipes[J]. Journal of Hydrodynamics (A), 2000, 15(1): 116－128. (in Chinese with English abstract)

[12] 杨超. 非恒定流充液管系统耦合振动特性及振动抑制[D]. 华中科技大学，2007. Yang Chao. Vibration Characteristics of Unsteady-fluid- filled Pipe System and Vibration[D]. Huazhong University of Science and Technology, 2007. (in Chinese with English abstract)

[13] 杨超，易孟林，李宝仁. 非稳定流输送管道的耦合振动[J]. 中国机械工程，2008，19(4)：406－410. Yang Chao, Yi Menglin, Li Baoren. Coupled vibration of piping system conveying unsteady flow[J]. Chinese mechanical engineering, 2008, 19(4): 406－410. (in Chinese with English abstract)

[14] 杨超，范士娟. 输液管道流固耦合振动的数值分析[J]. 振动与冲击，2009，28(6)：13－25. Yang Chao, Fan Shijuan .Numerical analysis of fluid-structure coupled vibration of fluid-conveying pipe[J]. Journal of Vibration and Shock, 2009, 28(6): 13－25. (in Chinese with English abstract)

[15] 陈婷，苏志敏，朱建兵，等. 基于FSI 的4-方程模型的改进分析[J]. 应用力学学报，2016，33(4)：565－569.Chen Ting, Su Zhimin, Zhu Jianbing, et al.Analysis and improvement of 4-equation based on FSI[J].Chinese Journal of Applied Mechanics, 2016, 33(4): 565－569. (in Chinese with English abstract)

[16] Ghodhbani A, Taïeb E H. A four-equation friction model for water hammer calculation in quasi-rigid pipelines[J]. International Journal of Pressure Vessels & Piping, 2017, 151: 54-63.

[17] Axworthy D H, Ghidaoui M S, Mcinnis D A. Extended thermodynamics derivation of energy dissipation in unsteady pipe flow[J]. Journal of Hydraulic Engineering, 2000, 126(126): 276－287.

[18] Bergant A, Tijsseling A S, Vítkovský J P, et al. Parameters affecting water-hammer wave attenuation, shape and timing—Part 1: Mathematical tools Paramètres affectant l'atténuation, la forme et le retard du coup de bélier—Partie 1: Modèles mathématiques[J]. Journal of Hydraulic Research, 2008, 46(3): 373－381.

[19] 李进平，李修树. 管道非恒定流摩阻损失研究[J]. 水利水电快报，2000(6)：7－11.Li Jinping, Li Xiushu. Research on the non-constant flow friction loss of pipeline[J]. Express Water Resources & Hydropower Information, 2000(6): 7－11. (in Chinese with English abstract)

[20] Keramat A, Tijsseling A S, Hou Q, et al. Fluid–structure interaction with pipe-wall viscoelasticity during water hammer[J]. Journal of Fluids & Structures, 2012, 28(1): 434－455.

[21] Riasi A, Nourbakhsh A, Raisee M. Energy dissipation in unsteady turbulent pipe flows caused by water hammer[J]. Computers & Fluids, 2013, 73(6): 124－133.

[22] Triki A. Water-hammer control in pressurized-pipe flow using an in-line polymeric short-section[J]. Acta Mechanica, 2016, 227(3): 777－793.

[23] Keramat A, Kolahi A G, Ahmadi A. Water hammer modelling of viscoelastic pipes with a time-dependent Poisson's ratio[J]. Journal of Fluids & Structures, 2013, 43: 164－178.

[24] Lavooij C S W, Tusseling A S. Fluid-structure interaction in liquid-filled piping systems[J]. Journal of Fluids & Structures, 1991, 5(5): 573－595.

[25] Ghidaoui M S, Zhao M, Mcinnis D A, et al. A review of water hammer theory and practice[J]. Applied Mechanics Reviews, 2005, 58(1): 49－76.

[26] Tijsseling A S. Fluid-structure interaction in case of water hammer with cavitation [J]. Thesis Technische Univ, 1993.

[27] Tijsseling A S. Exact solution of linear hyperbolic four- equation system in axial liquid-pipe vibration[J]. Journal of Fluids & Structures, 2004, 18(2): 179－196.

[28] Ghodhbani A, Hadj-Taïeb E. Numerical Coupled Modeling of Water Hammer in Quasi-rigid Thin Pipes[M]// Design and Modeling of Mechanical Systems. Springer Berlin Heidelberg, 2013.

[29] Tijsseling A S. Fluid-Structure Interaction in liquid-filled pipe systems: a Review[J]. Journal of Fluids & Structures, 1996, 10(2): 109－146.

[30] 范晓丹，刘韩生. 非恒定摩阻的TVD格式数值模拟水击衰减研究[J]. 水力发电学报，2017，36(3)：55－62. Fan Xiaodan, Liu Hansheng. Numerical simulations of water hammer attenuation due to unsteady friction using a TVD scheme[J]. Journal of Hydroelectric Engineering, 2016, 36(3): 55－62. (in Chinese with English abstract)

Calculation of water hammer pressure of flow pipeline based on modified four-equation friction model

Wang Zhenhua1,2※, Ma Xihe1,2, Li Wenhao1,2, Zheng Xurong1, Zhang Jinzhu1

(1.832000,2.832000,)

Water hammer problem is a problem that often occurs in the pipeline and is difficult to control. Friction coupling is a boundary contact coupling formed by the relative motion between the fluid and the wall of the tube to produce viscous friction. In the range of high frequency motion of the fluid, the characteristics of the friction coupling become more complex, which will directly affect the water hammer evolution of the pipeline system. At present, most numerical models of water hammer calculation are based on the constant flow friction equation of one-dimensional water hammer, ignoring the wall shear stress and convection item, and the attenuation and waveform distortion processes of water hammer pressure wave are difficult to make an accurate calculation. There are few studies on the friction coupling and connection coupling and convection term as to the pipe fluid water hammer calculation. Unsteady friction models are only validated with uncoupled formulation. Additionally, coupled models such as four-equation model (4EM), provide more accurate prediction of water hammer since fluid-structure interaction (FSI) is taken into account, but they are limited to steady-state friction formulation. In this paper, the four-equation friction model (4EFM) based on Zielke model and FSI 4EM is modified according to the one-dimensional unsteady flow shear stress on tube wall, which was derived from the extended irreversible thermodynamics (EIT) by Axworth and others, and the modified 4EFM can accurately reflect the influence of the unsteady friction term on the water hammer wave. In the self-pressure pipeline water delivery project on Hongxing Farm of Thirteenth Division, Xinjiang Production and Construction Corps, the closed valve water hammer test was performed, this model was applied to quasi rigid pipeline with axial movement valve, and the numerical calculation of closed valve water hammer in the pipeline was carried out by using the method of characteristics (MOC) with the MATLAB software. Then the accuracy of Zielke model, 4EM, 4EFM and modified 4EFM in the simulation of water hammer of the pipeline was compared and analyzed. The results show that under the friction coupling and junction coupling condition, Zielke model and 4EM are not suitable for calculating the change of pipeline water hammer, and numerical oscillation and the error are serious, in the third s two model pressure decay process, compared with measured data of early 0.5 s, phase deviation. The modified 4EFM and 4EFM can accurately describe the distortion and attenuation process of pressure wave after a cycle, the simulation deviation will not increase with time, the phase deviation is small, and the fit degree is high. The modified 4EFM has better consistency with the measured value through the comparison. The 4EFM and other calculation models have better consistency. The peak error of water hammer pressure in each cycle for the modified 4EFM is basically less than 1.5%, which is better than 4EFM with the pressure peak error of more than 3%. In practical engineering, in addition to the impact of objective conditions, water hammer pressure calculated by the modified 4EFM has high fitting degree with the tested data, as well as water hammer wave form and time, and this method can accurately capture the characteristics of the early change of pressure in long distance pipeline, the water hammer wave attenuation and the phase shift, so the modified model can be applied in water hammer calculation during long distance water transfer process of gravity flow with the computer. And the reduction of the time step of the operation can improve the simulation precision of the modified 4EFM. At present, the effect of the modified 4EFM on the calculation of water hammer in the environment of viscoelastic tube and multiphase flow still needs further verification.

water hammer; friction; coupling; method of characteristics; numerical simulation

10.11975/j.issn.1002-6819.2018.07.015

O353.1

A

1002-6819(2018)-07-0114-07

王振华，马习贺，李文昊，郑旭荣，张金珠. 基于改进4-方程摩擦模型的输水管道水锤压力计算[J]. 农业工程学报，2018，34(7)：114－120. doi：10.11975/j.issn.1002-6819.2018.07.015 http://www.tcsae.org

Wang Zhenhua, Ma Xihe, Li Wenhao, Zheng Xurong, Zhang Jinzhu. Calculation of water hammer pressure of flow pipeline based on modified four-equation friction model [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 114－120. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.07.015 http://www.tcsae.org

2017-12-05

2018-03-04

国家重点研发计划“自流灌区用水调控技术集成与应用示范”（2017YFC0403205）

王振华，男，河南扶沟人，教授，博士，博士生导师，主要从事干旱区节水灌溉理论与技术研究。Email：wzh2002027@163.com

中国农业工程学会会员：王振华（E041200608S）