嵌入地下水动力模型的井灌区机井布局耦合优化模型

贾艳辉，费良军，黄修桥，李金山，翟国亮



嵌入地下水动力模型的井灌区机井布局耦合优化模型

贾艳辉1,2，费良军1，黄修桥2※，李金山1,2，翟国亮2

（1. 西安理工大学水资源研究所，西安 710048； 2. 中国农业科学院农田灌溉研究所，新乡 453002）

为探索井灌区适宜的机井布局方法，降低井灌区提水能耗，构建了以取水费用最小为目标的机井布局优化模型并把地下水动力模型（Modflow-2000）嵌入其中，通过2模型中的公共参数进行数据交换，从而形成机井布局耦合模型。利用实测资料对模型中相关参数进行率定，最后以通辽井灌区为研究对象，采用黄金分割搜索法对灌区机井位置进行寻优。应用结果表明，利用该耦合模型可以精准模拟灌区地下水位，模拟值与观测值的相对误差绝对值的平均值为0.88%，RMSE值为0.135 3 m；与灌区目前机井布局方式相比，优化后的机井布局方式可以有效减小区域机井水位降深，单次提水灌区井群地下水位累积降深值可减少5.96 m（降深平均值减少0.134 m）；构建的耦合模型在确保模拟精度的前提下寻优速度快（单次运行时间仅需40 s）。为基于灌区地下水采补协调的机井空间布局优化提供了新的思路。

灌溉；井；耦合；优化；Modflow-2000；机井空间优化

0 引 言

《2015全国水利发展统计公报》中统计，截至2015年年底，全国已累计建成日取水大于等于20 m3的供水机电井或内径大于200 mm的灌溉机电井483.2万眼[1]。开发地下水保障了农业生产，但在地下水开发利用过程中缺乏科学规划，就会使机井装置效率低、耗能高，甚至影响地下水资源可持续高效开发利用。因此，研究机井布局方法对降低井灌区灌溉能耗及水资源可持续利用具有重要的理论与现实意义。

灌溉机井布局研究主要是机井数量，井距与空间位置的合理布设等方面。相关领域的学者对承压井和潜水井的布局做了大量研究，也取得了丰硕成果，已有研究结果大多集中于单井适宜的灌溉控制面积[2-5]、灌区合理机井数目[6-10]及适宜的井距[11-19]。与井数、井距方面的研究相比机井空间布局的研究还相对较少[20-27]，其中吴丹等[20-21]利用空间优化算法对灌区机井布局中井数、井距等进行了评价及优化计算，但该研究未考虑运行费用及水文地质条件、补给排泄条件等；张远东等[26]建立了以降深最小为目标函数的0～1整数规划管理模型，对区域地下水开采问题中的机井布局问题进行了优化，虽然考虑了运行费用及水文地址条件，但整数规划法可行域为离散集与实际井位置有差距。如何能在优化机井位置时，既考虑水文地质及地下水补给排泄条件对提水过程可以较真实的刻画，又能对机井位置进行连续的调整，是机井布局优化方面亟待解决的问题。

本文拟使用优化模型和地下水动力学模型相协调的耦合模型，充分发挥单一模型的自身优势，综合考虑研究区域具体水文地质及补给排泄条件，以灌区井群综合取水费用最小为目标，利用耦合模型对灌区机井位置进行连续寻优。并以通辽井灌区为研究对象，对该灌区（约6 km2耕地）机井空间布局进行优化。

1 数学模型构建

首先建立目标函数为模拟区综合取水费用最小的机井布局优化模型，并把地下水动力模型（Modflow-2000）嵌入到机井布局优化模型中，利用机井布局优化模型与地下水动力模拟模型之间的公共变量进行数据传递，从而得到机井布局耦合模型。模型结构如图1所示，耦合模型中的地下水动力模型部分（Modflow-2000）作为约束条件嵌入优化模型中，并通过地下水位、灌溉水量等公共参数进行数据传递。

1.1 机井布局优化模型

1）目标函数

以机井位置为决策变量，以灌区取水费用为目标函数，在灌溉制度一定时，机井提水灌溉费用与机井出水量、电价和水泵效率等有关。一般情况下，机井水位降深越小，一定灌水量的提水能耗就越小。本文对井位置进行优化时，以机井水位降深最小为目标，当机井水位累积降深达到最小时，提水费用也达到最小，反之亦然。因此，目标函数可用式（1）表达：

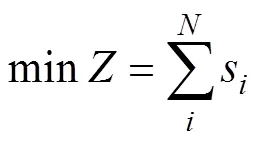
式中Z为目标函数，即灌区机井水位累积降深最小，m；N为需要累计的降深个数，即灌区机井总数；为灌区某一机井地下水位降深，m。

2）约束条件

环境约束，地下水位降深应该在合理范围：

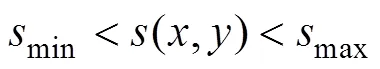
式中(,)为位置(,)的地下水降深，m；min为不发生次生盐碱化的地下水最小降深，m；max为不产生地下水超采漏斗的最大降深，m。

地下水位约束，地下水位一定在地表和隔水底板之间：

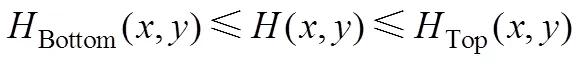
式中()Z为坐标()处的地下水位，m；()=Top()-()；Bottom()为坐标()处的潜水隔水底板高程，m；Top()为坐标()处的地面高程，m。

井位约束，按就近取水用水、方便管理的原则，灌溉井都布置在耕地边并靠近生产路：

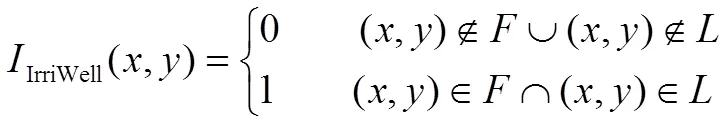
式中IrriWell(,)为灌溉机井位置约束，只有当位置(,)在耕地中并靠近路或居住区边界时才能布置机井；为耕地区域；为田间路或居住区边界的临域。

灌溉、生活用水约束，居住区生活及牲畜用水量及灌溉用水量按当地习惯给出。

水动力约束，模型中提水、补给及地下水位应符合地下水动力学规律。

1.2 地下水动力模拟模型

研究区域灌溉水源以潜水为主，含水层深度80 m左右，含水层补给源为地下水含水层上游侧向补给、降雨补给、灌溉水回补、河流侧渗补给等，排泄量主要有模拟区内居民生活及牲畜用水、灌溉提水、含水层向下游侧向补给。地下水概念模型如图2所示。

在补给及排泄量中因试验区水资源紧缺，故灌溉时不产生灌溉回水；通过查阅资料，试验区地下水补给主要依靠降雨入渗[28]，目前地表河流已经干涸，为简化模拟，不考虑河流侧渗补给量。

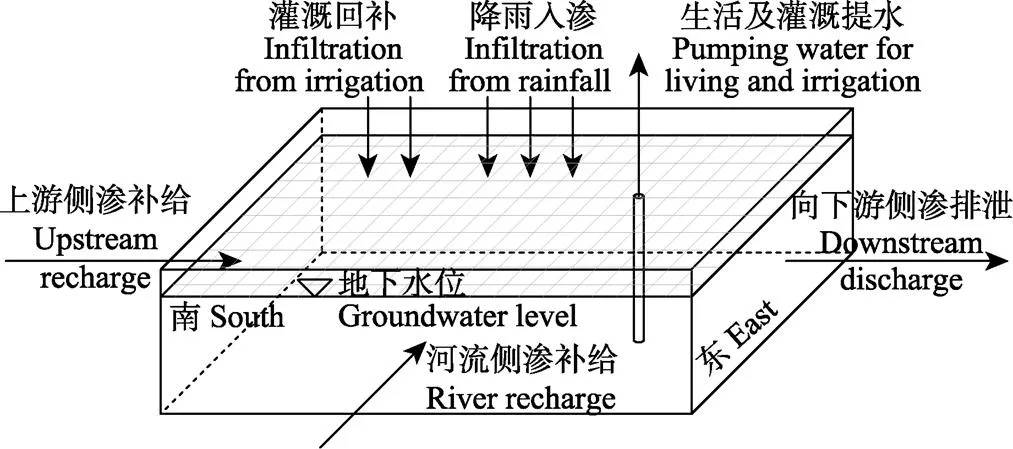
图2 地下水概念模型图

数学模型[29-30]：

式中为渗透系数，m/d；为地下水位，m。=-，为含水层厚度，m；为地下水深度，m；为源汇项，在本文中为单位体积的地下水抽水量（d-1）；为给水度（m-1）；为时间，d。

上边界条件为灌溉、降雨补给[31]

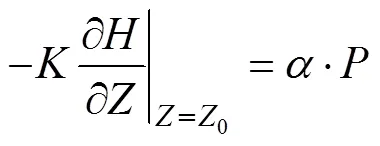
式中为坐标，为补给系数，z为模型地面，为降雨量，m/d。项目区四周边界处理为通量边界

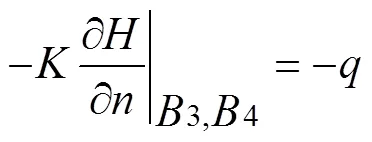
式中为边界法方向；1西边界，2为北边界，3为东边界，4为南边界；为上游来流量的分量，=0.004 14 m/d。

2 应用实例

研究区（44°05¢01.50²N，122°05¢46.21²E，东西长3.2 km，南北宽2.4 km）位于大兴安岭的东南边缘的科左中旗内，科左中旗是松辽平原向内蒙高原的过渡带。小区东西各分布1个村庄。西边村庄人口590人，生活 用水量26.6 m3/d；东边村庄人口519人，生活用水量 23.3 m3/d。东北方向临荒地，区域中耕地面积约6 km2，研究区域共有44眼灌溉机井，根据单井控制面积0.13 km2均匀布置，如图3所示。

本文拟使用耦合模型对现有44眼机井位置进行优化调整，得出小区的最优机井布设，作为灌区未来机井布局调整的参考。

2.1 Modflow-2000模型参数

分布式地下水动力模型（Modflow-2000）中，需要输入模型几何形状，水文地质参数，模拟时段信息、降雨、提水、灌溉信息和初始水位等信息。

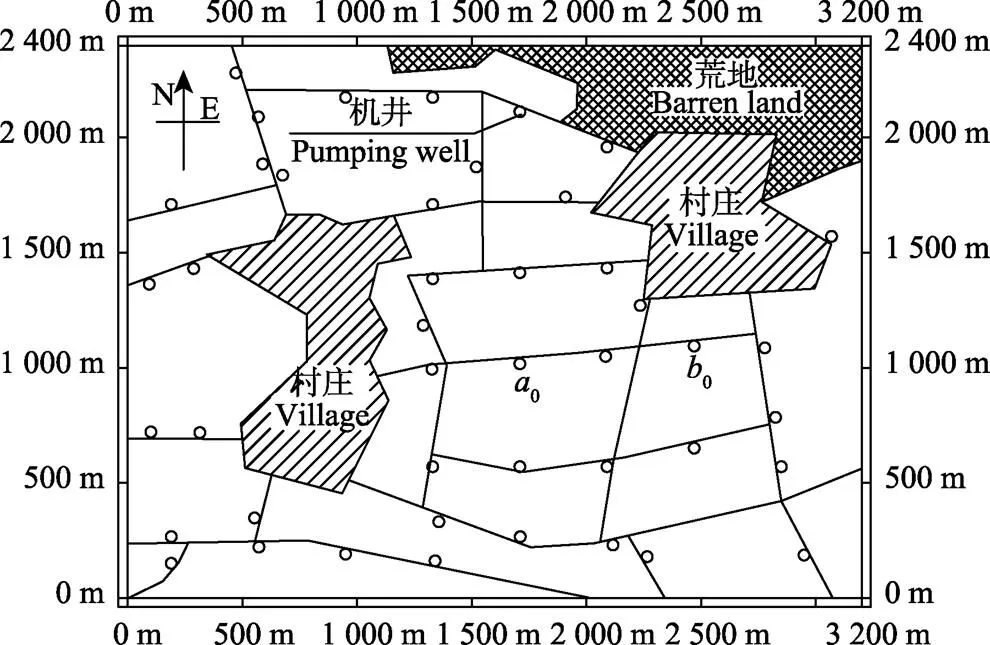
注：图中a0，b0为2.3.1节中第1井优化时的两边界

1）水文地质参数

科左中旗[32]地下水含水层主要为第四系堆积物中的浅层孔隙潜水及第三系地层中的深层承压水。含水层厚度达80~100 m以上。含水层岩性主要为松散的粉细砂，含水层透水性良好，水量丰富，区内第四系地层中的潜水埋深一般为2~10 m，上第三系地层中的承压水埋深则在100 m以上，地下水动态类型属入渗—蒸发型。区内降水对地下水补给占总补给量的70%以上，区外地下径流也补给一部分。地下水的排泄主要为垂直蒸发，人工开采和侧向径流。地下水径流为由西北向东南与地形一致，水力坡度为1.2‰左右。

地下水含水层主要为第四系堆积物中的浅层孔隙潜水。根据项目区现有机电井的运行情况，当井深达到60~80 m、水位降深在3.66~7.93 m时，单井出水量在50~ 80 m3/h以上。

模拟所需的水文地质参数包括地下水渗透系数及给水度。通过腰林毛都镇进行的抽水试验，计算得，渗透系数=4.88 m/d，=0.16。

2）应力期

模拟期时长64 a，分为192个应力期，每个应力期为4个月，并平均分为3个等长时段。在一年中1月—4月为第一应力期，只有降雨补给和生活用水；5月—8月为第二应力期，为作物生长、灌水季节，包括降雨补给、灌溉和生活用水；9月—12月为第三应力期，只有降雨补给和生活用水。

3）降雨补给量

选用李曙光等[28]应用1980—2005年的降雨资料计算的数据=0.178 3作为模型输入值。降雨量使用1951—2014年通辽气象站的降雨数据作为模型输入值。

4）灌溉定额

根据当地耕作经验及历史降雨资料，将喷灌灌溉定额按年降雨量分为5种：①降雨量≤300 mm，灌溉定额=262.5 mm（37.5 mm´7次）；②降雨量300 mm<≤350 mm，灌溉定额=225 mm；③降雨量350 mm<≤400 mm，灌溉定额=187.5 mm；④降雨量400 mm<≤450 mm，灌溉定额=150 mm；⑤降雨量≥450 mm，=112.5 mm。

2.2 模型参数检验

把抽水试验计算的水文地质参数输入到地下水动力学模型（Modflow-2000）中，采用2015年的地下水位监测数据，进行模型参数检验。模拟值与实测值分析结果（图4）表明，模拟值与观测值均匀分布在1：1线两侧（图4a）；进一步分析发现（图4b），观测井不同时段水位观测值与模拟值的变化趋势基本一致，模拟值与观测值相对误差绝对值介于0.002 4%～4.117 1%，相对误差绝对值的平均值为0.88%（=25），RMSE值为0.135 3 m，完全可以满足地下水资源优化配置的需求，说明构建的耦合模型能够反映灌区井群地下水位的实际变化趋势。

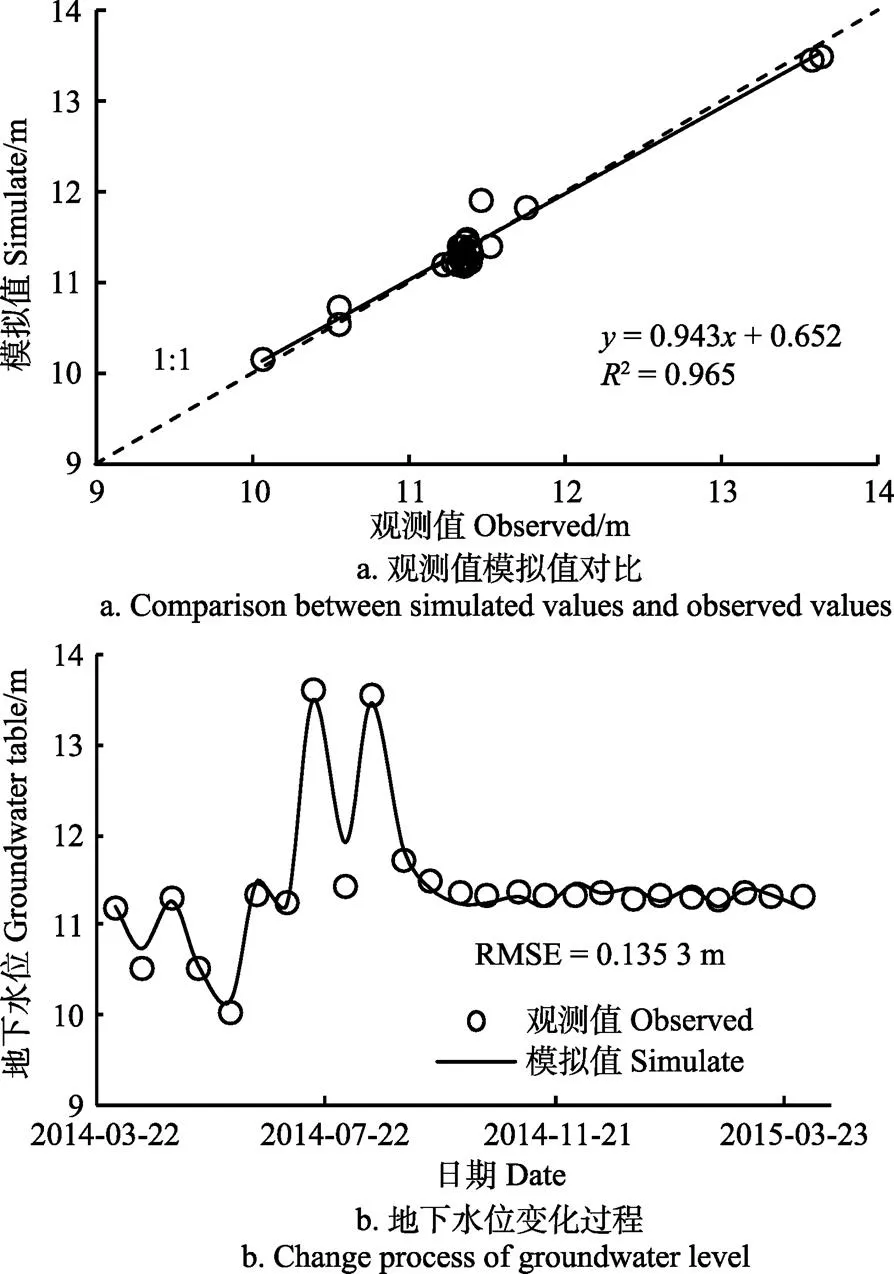
图4 地下水位模拟值与观测值对比

2.3 耦合模型优化过程

井位优化本来是在二维空间中进行优化，但目前灌溉用井为建设、管理方便，一般布置在路附近。这样单井位置优化就变为一维问题。但是由于优化模型中嵌入了分布式地下水动力学模型，不能使用数学规划方法直接计算。本文使用黄金分割法进行迭代求解。

2.3.1 优化流程

在区域内选择1井，作为待优化井，找到待优化机井沿路相邻的2机井作为迭代范围（0，0），在迭代范围内选择两黄金分割点1、1¢，分别把两点带入Modflow- 2000模型进行模拟计算，得到降深累积值1和1¢，如1<1¢，令1=0，1=1¢；否则令1=1，1=0。然后在（1，1）中重复上面的迭代过程，直到2次结果相差满足预设的精度要求为止。再选择第2口井进行寻优，以此类推直至所有井的位置都为最优时，这种机井布置形式就是研究区域的最优机井布置方式。优化流程见图5。

2.3.2 单井位置搜索过程

现对其中1井进行介绍，单井优化使用黄金分割搜索法[12]。首先找到需要优化井沿路或沿村边界的临井，把临井井位作为优化井的边界井位（西边临井位置为0，东边临井位置为0），如图3所示。在区间（0，0）中选择0.382倍00区间长度和0.618倍00区间长度的两点1，1¢。把1和1¢分别做为机井位置代入Modflow-2000模型进行计算，得到降深累积值1和1¢，如1<1¢，令1=0，1=1¢；否则令1=1，1=0。然后在（1，1）中再进行进一步迭代，直到满足寻优精度要求(|f(t)-(t¢)|<0.01)为止。详细步骤见文献[33]。

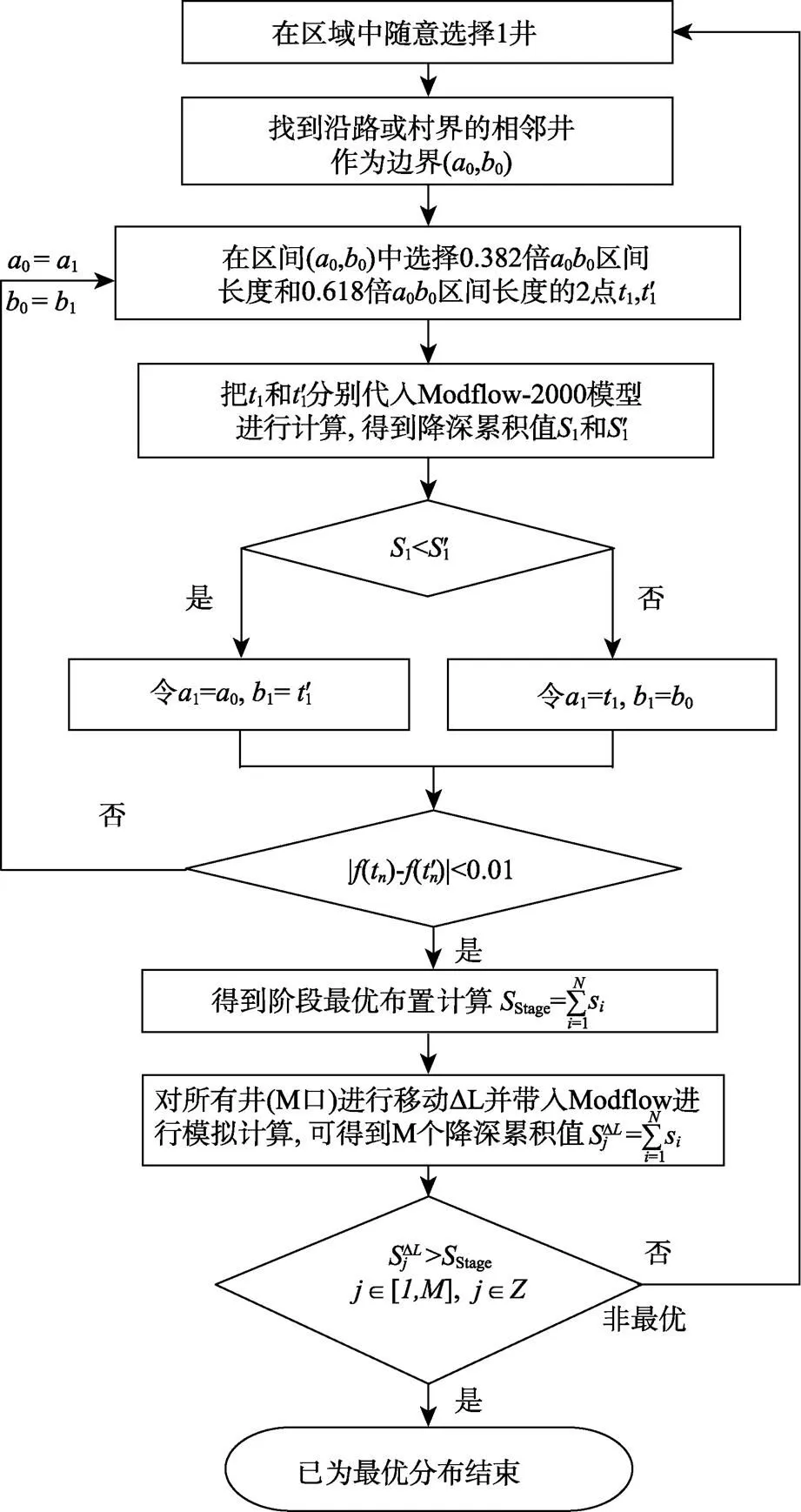
注：图中S1和S1'分别为井位t1和 t1'对应的累积降深，m；SStage为阶段最优分布对应的累积降深，m；Sj△L为第j井移动△L后得到的累积降深，m；si为各井降深，m；f(tn)为tn点的累积降深值，m。

根据上面搜索原理，使用VB编写程序，首先确定1待优化井（坐标）及优化边界井（坐标）输入到程序中，程序读入两坐标后内插两黄金分割点（1、1¢）并计算两点坐标；然后程序根据两点替换待优化井坐标并生成2个Modflow-2000井文件（t1.WEL，t1¢.WEL）、2个头文件（t1.NAM，t1¢.NAM）及两个DOS批处理文件（t1.BAT，t1¢.BAT）；接着程序调用2个批处理文件运行2次Modflow-2000，分别得到水头结果文件t1.HED，t1¢.HED；最后程序根据井位置及水头结果文件提取各机井降深并计算两降深累计值1和1¢，比较两值，如不满足精度要求则进入下一次迭代，如满足精度要求则输出结果。

Modflow-2000模型单次运行需40 s（Intel i5处理器），单井寻优平均需运行Modflow- 2000模型10次，单井时长约8 min。

灌区机井地下水位最小降深累积值为1 277.78 m，最小累积降深机井位置坐标（2 326.82，1 079.89）。第1井最优井位机井地下水位变化过程如图6所示。

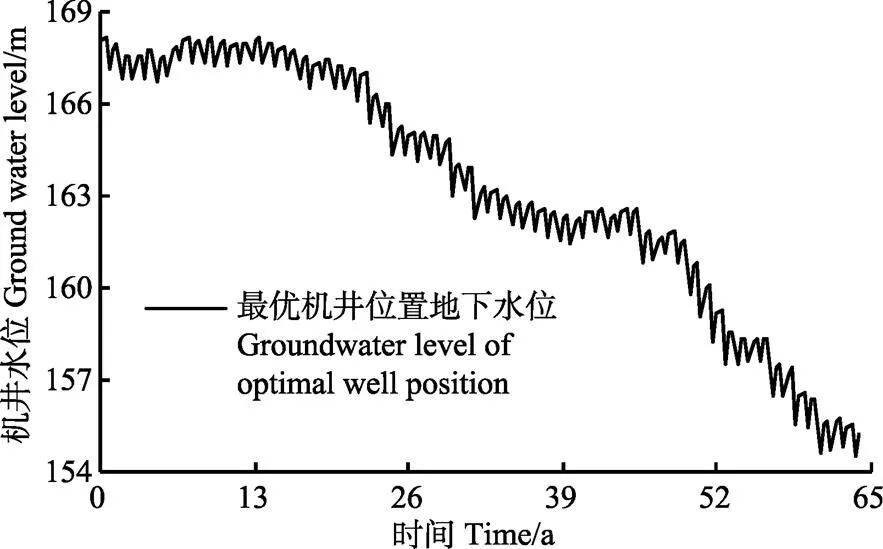
图6 最优位置机井水位变化过程

2.3.3 优化结果

上节完成了1个井1次的寻优过程，再选择1井进行同样过程的优化（同1井会被多次选择并优化），直到满足误差条件为止。经过多次运行程序，可以达到全局最优（在实际优化过程中，从四周开始，可以减少优化次数），研究区最优机井布设如图7所示。

图7 最优井位分布

最优布置与现有布置相比，单次提水研究区机井地下水位降深累积值可减少5.96 m，机井降深平均值减少0.134 m。

3 结果与分析

通过上面的对通辽井灌区实地情况的概化及地下水动力学模型的参数识别后，使用灌区64 a的气象数据，对各种井位置进行模拟并优化，得到以下优化结果：

1）从单次优化结果（图6）看，机井水位呈现波动下降趋势。地下水位在持续下降，说明研究区即使使用喷灌，灌溉定额（平水年灌溉定额=225 mm）依然偏大，如要保持该地区水资源平衡，应减少灌溉用水，使用滴灌等更节水的技术。

2）单井优化结果中，最优井位并不在相邻2井中间位置，而是在相邻2井区间的3/4处，这是由于小区东北部荒地及村庄无灌溉用井，对耕地的地下水有补给作用。

3）对比图7与图3可以看出，距村庄和荒地越近，机井分布的密度越大，距村庄和荒地越远，机井分布密度越小，说明局部的补给条件变化对附近影响较大。如区域中无补给条件的差别，本文中的机井布局优化结果将与井距法得出的结果相同。

4）从全局优化结果看，与目前井距法结果相比（图3）机井分布有较大变动，单次提水降深累积值比目前的井距法可减少5.96 m（降深平均值减少0.134 m），对小区的能耗降低有一定作用。

从图4a和图4b可看出，Modflow-2000模拟值与观测值吻合较好，可作为地下水管理有效的工具。地下水运动是一个复杂的系统，文中模型概化较简单，与真实流场有一定差距。但应用在验证耦合模型对井群布局的优化方面，也能在一定程度上说明问题。单个机井的优化过程已经做到自动寻优，但是多井寻优过程较繁琐。下一步要研究选井、确定寻优边界等算法，减轻人工 强度。

如果把模拟情景设置为基坑降水，机井沿基坑周围设置，耦合模型就可以优化基坑降水问题；如果调整提水为注水，耦合模型还可以优化地下水人工回灌井布局问题。

4 结 论

通过构建耦合模型并使用逐井迭代方法对机井位置优化问题进行探讨，得出以下结论：

1）单次优化结果发现研究区即使使用喷灌，机井水位依然呈现持续波动下降趋势，说明灌溉定额（平水年灌溉定额=225 mm）偏大，如要保持该地区水资源平衡，应减少灌溉用水，使用滴灌等更节水的技术。

2）使用机井布局优化模型与地下水动力模型（Modflow- 2000）得到的耦合模型，对井灌区机井布局进行规划与传统井距方法得到的结果相比，机井累积降深5.96 m，展示耦合模型可以起到降低能耗的效果，推荐使用此模型进行机井布局规划。

3）使用黄金分割法求解耦合模型是可行的，单井寻优平均需运行Modflow-2000模型10次。单井的寻优已做到自动运行，但多井寻优过程相对较繁琐。下一步要研究选井、确定寻优边界等算法，减轻人工强度，提高效率。

[1] 中华人民共和国水利部. 2015年全国水利发展统计公报[M]. 北京：中国水利水电出版社，2016：9.

[2] 胡艳玲，齐学斌，黄仲冬，等. 基于补排平衡法的井渠结合灌区机井数量研究[J]. 灌溉排水学报，2015，34(8)：17－21.

Hu Yanling, Qi Xuebin, Huang Zhongdong, et al. Study on amount of pump well in well-canal combined irrigated area based on the balance of supplement-exhaust[J].Journal of Irrigation and Drainage, 2015, 34(8): 17－21. (in Chinese with English abstract)

[3] 李建承. 北方大型灌区渠井结合配置模式研究[D]. 杨凌：西北农林科技大学，2015.

Li Jiancheng. Study on Northern Large Irrigation District Canal-Well Combined Configuration Mode[D]. Yangling: Northwest A&F University, 2015. (in Chinese with English abstract)

[4] 姜瑞忠，刘明明，徐建春，等. 遗传算法在苏里格气田井位优化中的应用[J]. 天然气地球科学，2014，25(10)： 1603－1609.

Jiang Ruizhong, Liu Mingming, Xu Jianchun, et al. Application of genetic algorithm for well placement optimization in Sulige Gasfield[J]. Natural Gas Geoscience, 2014, 25(10): 1603－1609. (in Chinese with English abstract)

[5] 何玲，王海艳，康银红，等. 单井控制灌溉面积计算[J]. 农业工程，2013，3(1)：54－56.

He Ling, Wang Haiyan, Kang Yinhong, et al. Calculation of single-well control area[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 3(1): 54－56. (in Chinese with English abstract)

[6] Hongbin Zhan, Jiang Cao. Analytical and semi-analytical solutions of horizontal well capture times under no-flow and constant-head boundaries[J]. Advances in Water Resources, 2000, 23(8): 835－848.

[7] 康琪. 低渗透油田低泵效抽油机井治理研究[J]. 化学工程与装备，2014(5)：85－87.

[8] 韩二涛，李明，郑华，等. 低渗透油田抽油机井系统效率现状及对策[J]. 石油化工应用，2013，32(9)：117－120.

Han Ertao, Li Ming, Zheng Hua, et al. Present situation and improved measure of pumping well system efficiency at Changqing low-permeability oilfield[J]. Petrochemical Industry Application, 2013, 32(9): 117－120. (in Chinese with English abstract)

[9] Wang K B, Ma W K, Meng X G, et al. The design of emergency rescue equipment for agricultural motor- pumped wells[J]. Applied Mechanics & Materials, 2014, 488-489: 1104－1107.

[10] Khare D, Jat M K , Ediwahyunan. Assessment of conjunctive use planning options: A case study of Sapon irrigation command area of Indonesia [J]. Journal of Hydrology, 2006, 328(3): 764－777.

[11] 刘万顺. 对灌溉井井距问题的探讨[J]. 农田水利与水土保持，1965，(9)：23－24.

[12] 段玉德. 井距计算新方法[J]. 地下水，1985，(2)：60－61.

[13] 王红雨，全达人. 井灌区规划井距的确定方法[J]. 灌溉排水，1995，(4)：41－44.

[14] 何东博，王丽娟，冀光，等. 苏里格致密砂岩气田开发井距优化[J]. 石油勘探与开发，2012，39(4)：458－464.

He Dongbo, Wang Lijuan, Ji Guang, et al. Well spacing optimization for Sulige tight sand gas field, NW China[J]. Petroleum Exploration and Development, 2012, 39(4): 458－464. (in Chinese with English abstract)

[15] 徐强，雷明信. 某地浸矿床抽注液井距研究：Visual- MODFLOW在某地浸矿山井距确定中的应用[J]. 中国矿业，2012，21(S1)：628－630.

Xu Qiang, Lei Mingxin. The research on interval between pump and affusion well of insite uranium mine[J]. China Mining Magazine, 2012, 21(S1): 628－630. (in Chinese with English abstract)

[16] 臧海洋. 沈阳城区地下水源热泵适宜性评价及应用模式研究[D]. 沈阳：沈阳建筑大学，2011.

Zang Haiyang. The Research of the Suitability and Application Pattern on Groundwater Source Heat Pump in Shenyang[D]. Shenyang: Shenyang Jianzhu University, 2011. (in Chinese with English abstract)

[17] 董艳慧. 地下水保护理论及修复技术的研究[D]. 西安：长安大学，2010.

Dong Yanhui. The Protection Theory and Recovery Technology of Groundwater[D]. Xi’an: Chang’an University, 2010. (in Chinese with English abstract)

[18] Willems C J L, Nick H M, Goense T, et al. The impact of reduction of doublet well spacing on the Net Present Value and the life time of fluvial Hot Sedimentary Aquifer doublets [J]. Geothermics, 2017, 68: 54－66.

[19] Nugrahanti A, Fathaddin M T. The impact of permeability and well spacing on well productivity in a coalbed methane reservoir[J]. International Journal of Civil Engineering & Technology, 2017, 8(11): 236－244.

[20] 吴丹，吉红霞，刘玉，等. 华北平原土地整治项目区农用机井的空间布局优化[J]. 经济地理，2015，35(6)：154－160. Wu Dan, Ji Hongxia, Liu Yu, et al. Optimizing the distribution of pumping wells for agricultural land consolidation in the North China Plain[J]. Economic Geography, 2015, 35 (6): 154－160. (in Chinese with English abstract)

[21] 吴丹. 井灌区农用机井的空间布局优化研究[D]. 西安：西安科技大学，2014.

Wu Dan. Study on the Spatial Layout Optimization of Agricultural Motor-pumped Wells in Irrigation Area[D]. Xi’an: Xi’an University of Science and Technology, 2014. (in Chinese with English abstract)

[22] 刘鑫，王素芬，郝新梅. 红崖山灌区机井空间布局适宜性评价[J]. 农业工程学报，2013，29(2)：101-109，304.

Liu Xin, Wang Sufen, Hao Xinmei. Suitability assessment on spatial layout of pumping wells in Hongyashan irrigation district[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(2): 101- 109, 304. (in Chinese with English abstract)

[23] 李彦刚，魏晓妹，蔡明科，等. 基于供需水量平衡分析的灌区机井布局模式[J]. 排灌机械工程学报，2012，30(5)，614－620.

Li Yangang, Wei Xiaomei, Cai Mingke. et al. Wells distribution layout in irrigation district based on water supply and demand balance analysis[J]. Journal of Draninage and Irrigation Machinery Engineering, 2012, 30(5): 614－620. (in Chinese with English abstract)

[24] 李彦刚. 灌区机井合理布局理论与方法研究[D]. 杨凌：西北农林科技大学，2009.

Li Yangang. Study on the Theories and Methods of Rational Layout of Pumped Wells in Irrigation District[D]. Yangling: Northwest A&F University, 2009. (in Chinese with English abstract)

[25] Hassan F H, Ibrahim N, Kit H W, et al. Incorporating genetic algorithm operators in optimization spatial layout design[C]// the International Conference. 2017: 179－183.

[26] 张远东，魏加华，邵景力，等. 0-1整数规划在水源地开采井最优布局中的应用研究[J]. 第四纪研究，2002，22(2)：141－147.

Zhang Yuandong, Wei Jiahua, Shao Jingli, et al. Study on application of 0-1 integer programming to the optimal layout of pumping wells in a well field[J]. Quaternary Sciences, 2002, 22(2): 141－147. (in Chinese with English abstract)

[27] 张嘉星，齐学斌，乔冬梅. 农业灌区机井规划布局研究进展[J]. 农学学报，2016，6(2)：96－100.

Zhang Jiaxing, Qi Xuebin, Qiao Dongmei. Research process of motor-pumped well planning layout in agricultural irrigation district[J]. Journal of Agriculture, 2016, 6 (2): 96－100. (in Chinese with English abstract)

[28] 李曙光，肇志强. 通辽市科尔沁左翼中旗地下水资源调查评价[J]. 内蒙古水利，2014，(1)：103－104.

[29] Harbaugh A W, Banta E R, Hill M C, et al. MODFLOW- 2000, the U.S. geological survey modular ground-water flow model-User guide to modularization concepts and the ground-water flow process[M]. U.S. Geological Survey, 2000.

[30] Mohammadzadeh H, Dadgar M A, Nassery H. Prediction of the effect of water supplying from Shirindare dam on the Bojnourd aquifer using MODFLOW2000[J]. Water Resources, 2017, 44(2): 216－225.

[31] Rashid H, Al-Shukri H, Mahdi H. Optimal management of groundwater pumping of the cache critical groundwater area, Arkansas[J]. Applied Water Science, 2015, 5(3): 209－219.

[32] 董文荣. 科左中旗农业灌溉效率研究[D]. 呼和浩特：内蒙古农业大学，2015.Dong Wenrong. Study on the Agricultural Irrigation Efficiency of Kezuozhongqi[D]. Hohhot: Inner Mongolia Agricultural University, 2015. (in Chinese with English abstract)

[33] 《运筹学》教材编写组. 运筹学(修订版)[M]. 北京：清华大学出版社，1990.

Coupling optimization model embedded groundwater dynamic model for distribution of pumping wells in well irrigation area

Jia Yanhui1,2, Fei Liangjun1, Huang Xiuqiao2※, Li Jinshan1,2, Zhai Guoliang2

(1.710048,; 2.453002,)

It is important to study the method of well layout to reduce the irrigation energy consumption and to promote the sustainable utilization of water resources. This paper aimed to explore the suitable layout method of well to reduce the water consumption in well-irrigation area. The optimization model of well layout was constructed with the minimum cost of water intake, in which the groundwater dynamic model (Modflow-2000) was embedded. And the data were exchanged through the common parameters of the 2 models, thus forming the coupling model of well layout. Based on the measured data, the trend of the observation value of the water level was consistent with that of the calculated value at different time after the corresponding parameters of the model were determined. And the mean value of the absolute relative error was 0.88%, and RMSE (root mean square error) value was 0.135 3 m, which could meet the accuracy requirements of the optimal allocation of groundwater resources. It showed that the model could reflect the actual change trend of groundwater level in irrigation area. Finally, taking Tongliao well-irrigation area in Inner Mongolia as the research object, the golden section search method was used to find the optimal positions of the pumping wells. The fluctuation of the water level in wells showed that the irrigation quota in the research area was too large and the irrigation water should be reduced to keep the water resource balance. The results of single well optimization were different from those of the existing well-spacing method. It was found that there were no irrigation wells in the northeastern uncultivated land and villages, and the optimal well location was not in the center position of adjacent 2 wells in the single well optimization results. From the results of global optimization, there was a great change in the distribution of wells compared with the current method of well spacing. And the cumulative value of drawdown in single water extraction could reduce by 5.96 m, and the average value of drawdown could reduce by 0.134 m, which had a certain effect on the decrease of energy consumption in the community. The groundwater movement is a complex system and the model generalization is simpler. Moreover, there is a certain gap with the real flow field. But the application of the coupling model to the optimization of the distribution of well group can also be explained to some extent. The optimization process of single well has reached automatic optimization, and the Modflow-2000 model averagely needs to be operated 10 times in single operation. Meanwhile, the time for single well is about 8 min long. But the process of multi-well optimization is cumbersome. If the model scenario is set to the foundation pit dewatering and the well is set around the foundation pit, the coupling model can optimize the dewatering of the foundation pit; if the water injection is adjusted, the coupling model can also optimize the layout of the artificial recharge well.

irrigation; wells; couplings; optimization; Modflow-2000; wells space optimization

2017-09-12

2018-02-12

国家重点研发计划课题（2017YFC0403204）；“十二五”农村领域国家科技计划课题（2014BAD12B05）；中国农业科学院创新工程协同创新行动CAAS-XTCX2016008

贾艳辉，助理研究员，博士，主要从事节水灌溉理论与技术研究。Email：jyh_5151@126.com

10.11975/j.issn.1002-6819.2018.07.013

S275.1

A

1002-6819(2018)-07-0100-07

贾艳辉，费良军，黄修桥，李金山，翟国亮. 嵌入地下水动力模型的井灌区机井布局耦合优化模型[J]. 农业工程学报，2018，34(7)：100－106. doi：10.11975/j.issn.1002-6819.2018.07.013 http://www.tcsae.org

Jia Yanhui, Fei Liangjun, Huang Xiuqiao, Li Jinshan, Zhai Guoliang. Coupling optimization model embedded groundwater dynamic model for distribution of pumping wells in well irrigation area[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 100－106. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.07.013 http://www.tcsae.org