基于应力路径试验的小麦粮堆力学特性和应力应变关系模型

蒋敏敏，陈桂香



基于应力路径试验的小麦粮堆力学特性和应力应变关系模型

蒋敏敏1,2，陈桂香1,2

（1. 河南工业大学土木建筑学院，郑州 450001；2. 粮食储运国家工程实验室，郑州 450001）

粮仓中粮堆在装卸时存在着复杂的应力路径，为了得出复杂应力路径对粮堆模量和临界状态特性的影响规律，以及粮堆应力应变关系模型，该文在侧向应力50～300 kPa下，进行了常规三轴压缩（conventional triaxial compression，CTC）、等压缩（constant mean normal stress compression，CMS）、三轴主动压缩（reduced triaxial compression，RTC）三轴应力路径试验，分析了应力路径和侧向压力对模量的影响和粮堆临界状态特性；修正岩土体三次曲线模型，建立了适于描述仓内小麦粮堆应力应变的模型，并通过应力路径试验结果和文献试验结果对模型的适用性进行验证。研究结果表明：各应力路径下初始模量、割线模量50均随着侧向应力呈幂函数增长；CTC、CMS试验的割线模量50比初始模量发生较大的降低，而RTC试验没有明显降低。在参考压力（大气压力）下，对于初始模量，CTC试验的结果最大，RTC试验的结果最小；对于割线模量50，CTC试验的结果最小，RTC试验的结果最大。CTC试验的初始模量、割线模量均随着侧向应力增长最慢，而RTC试验的结果均随着侧向应力增长最快。不同应力路径和侧向应力下，试验的破坏点均落于同一临界状态线上，小麦粮堆临界状态应力比为0.976。修正三次曲线模型反映了粮堆强度、峰度系数和峰值应变等特性，并通过8个参数进行计算；通过应力路径试验结果和文献试验结果对该模型进行了验证。研究结果可为粮仓装卸料压力、变形的计算提供更符合实际应力路径条件的参量，建立的修正三次曲线模型可用于粮堆应力和变形的数值模拟，为粮仓的设计提供参考。

应力；应变；模型；小麦粮堆；应力路径三轴试验

0 引 言

粮仓是重要的基础设施，中国各地粮仓中粮食储藏总量达2亿t，保障粮食安全是农业现代化的重要任务。中转仓、储备仓等各类粮仓在储藏周期结束后均需要进行装卸粮，此时粮仓中不同位置粮堆的竖向和侧向应力将发生复杂的变化，并会进一步作用在仓壁上，引起仓体结构的开裂、破坏、失稳等问题[1-5]。因此不同加卸载路径下粮堆的力学特性对粮仓极为重要[6-7]。

粮仓内粮堆是由粮食籽粒堆聚而成的散粒体，不少研究者对粮堆的力学特性和参数进行了研究，Moya等[8]、Afzalinia等[9]利用直剪、压缩试验，得出不同品种粮堆的单向压缩、直剪抗剪强度等性质。曾长女等[10-11]利用三轴试验，得出了小麦粮堆孔隙率、含水率对抗剪强度的影响规律。许启铿等[12]将小麦粮堆的三轴应力应变曲线分为4个阶段，得出弹性模量的变化规律。陈家豪等[13]根据三轴试验提出小麦粮堆模量的计算式，得出各阶段模量的特性。Stasiak等[14]利用声波法测得谷物、油菜籽的弹性模量，并得出了弹性模量随着压力的增长规律。程绪铎等[15-19]通过三轴等试验得出小麦、玉米、稻谷、大豆等粮堆的密度、弹性模量、体变模量，并分析了含水率、围压等因素对各力学指标的影响。蒋敏敏等[20]研究小麦粮堆直剪强度和剪胀特性，得出强度参数和剪胀角的分布范围，提出剪胀发展规律，得出最大剪缩体变、最大剪胀体变的变化范围。Nielsen[21]提出粮仓内粮堆应力应变模型对粮仓压力的计算极为重要。研究者还提出利用岩土本构理论反映粮堆的力学性质。姜勇等[22]采用了Duncan-Chang模型研究了筒仓内粮堆应力，但该模型不能反映周围压力降低的情况和剪胀性。Ayuga等[6,23]在筒仓卸料数值研究中，提出采用Drucker-Prager模型模拟粮堆力学性质。

目前在粮堆强度、模量等参量的研究，利用岩土本构模型计算粮堆的应力应变，均有相当多的研究成果。然而粮仓在装卸料等过程中，粮堆中的应力路径发生复杂变化，装粮时竖向加载，卸粮时竖向卸载，常规三轴和直剪试验难以反映粮仓中复杂应力路径的影响。现有的岩土模型是否完全适用于描述粮堆的力学特性，仍有待验证。

应力路径试验通常用来研究复杂堆载、开挖卸荷时地基和结构的应力变形[24-27]。模量是粮堆应力变形计算的关键参量，临界状态特性反映了装卸粮时破坏面力学特性。本文通过应力路径三轴试验，模拟粮仓中不同深度以及不同加卸载应力路径条件，得出各应力路径下模量规律和临界状态特性，分析粮堆强度、应力应变参数规律，修正土石料应力应变的三次曲线模型，提出适于模拟各种应力路径下粮堆应力应变关系的模型。为粮仓装卸料荷载、变形的计算提供了更符合实际应力路径条件的参量结果；应力应变模型应用于粮仓数值计算中，得出更符合实际的应力和变形规律，可为粮仓的设计计算提供理论基础。

1 材料与方法

1.1 试验材料和设备

本研究采用的试验材料为郑州产小麦，品种是郑麦113。根据散体材料三轴试验的规定[28]，试验中试样为圆柱形，直径为61.8 mm，高度为125 mm，密度为0.85 g/cm3，质量含水率为10.9%，小麦籽粒平均直径为4.5 mm。试样直径与籽粒平均直径的比值为13.7，符合三轴试验关于试样直径与颗粒直径之比不小于10的要求[28]。试验在全自动三轴仪中进行，将制成的圆柱形小麦粮堆试样放入三轴压力室中，施加侧向压力和轴向压力，侧向压力和轴向压力分别独立作用于试样上。

1.2 应力路径试验方案

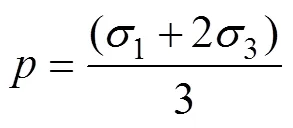
首先对粮堆试样施加各向相等的压缩应力，模拟粮仓内粮堆受到的初始周围压力，再通过独立控制轴向应力和侧向应力，实现对粮堆试样施加不同应力路径的作用。应力路径包括常规三轴压缩（conventional triaxial compression，CTC）、等压缩（constant mean normal stress compression，CMS）、三轴主动压缩（reduced triaxial compression，RTC）3种。常规三轴压缩试验中，保持侧向应力不变，增加轴向应力；等压缩试验中，降低侧向应力，同时增加轴向应力，并保持平均法向应力为常数；三轴主动压缩试验中，保持轴向应力不变，降低侧向应力。在-平面上，试验应力路径如图1所示。根据大型粮仓中粮堆的压力范围，各类应力路径试验的初始侧向应力设定为6个等级：50、100、150、200、250、300 kPa。试样剪切直至达到临界状态，即随着应变的增大，偏应力为常数（偏应力达到30%）[29]。各组试验均重复3次，因模量、强度的变异系数均小于2%，本文试验结果取3次结果的平均值。

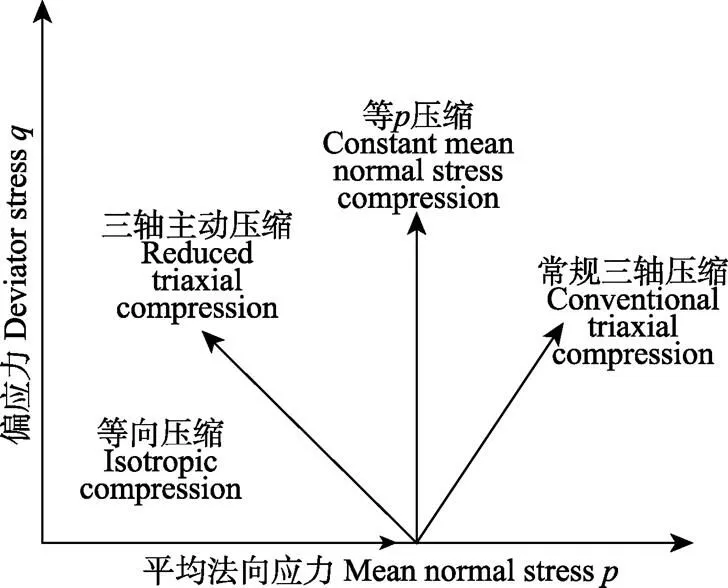
图1 小麦粮堆三轴应力路径试验示意图

2 结果与分析

2.1 模量和临界状态特性

2.1.1 模量特性

各类应力路径和不同侧向应力下小麦粮堆的应力应变曲线如图2所示。根据图2分析各试验的峰值偏应力（应力应变曲线最高值）和残余偏应力（轴向应变大于15%后的稳定值）结果，侧向应力介于50至300 kPa时，CTC试验的峰值偏应力介于98.3至400.4 kPa，残余偏应力介于92.7至373.5 kPa，CMS试验的峰值偏应力介于51.2至244.4 kPa，残余偏应力介于43至232.5 kPa，RTC试验的峰值偏应力介于23.9至136 kPa，残余偏应力介于15.2至60.8 kPa。相同侧向应力下，CTC试验的偏应力最大，RTC试验的偏应力最小；CTC试验应力应变曲线总体呈应变硬化型，RTC试验结果总体呈应变软化型[29]。CTC试验的侧向应力不变，轴向应力不断增大，侧向应力的约束能增大粮堆的刚度，粮堆表现出硬质材料的特性，因此偏应力大，材料呈应变硬化[29]。RTC试验的侧向应力不断减小，轴向应力不变，侧向的约束效应最小，粮堆表现出软质材料的特性，因此偏应力小，材料呈应变软化。

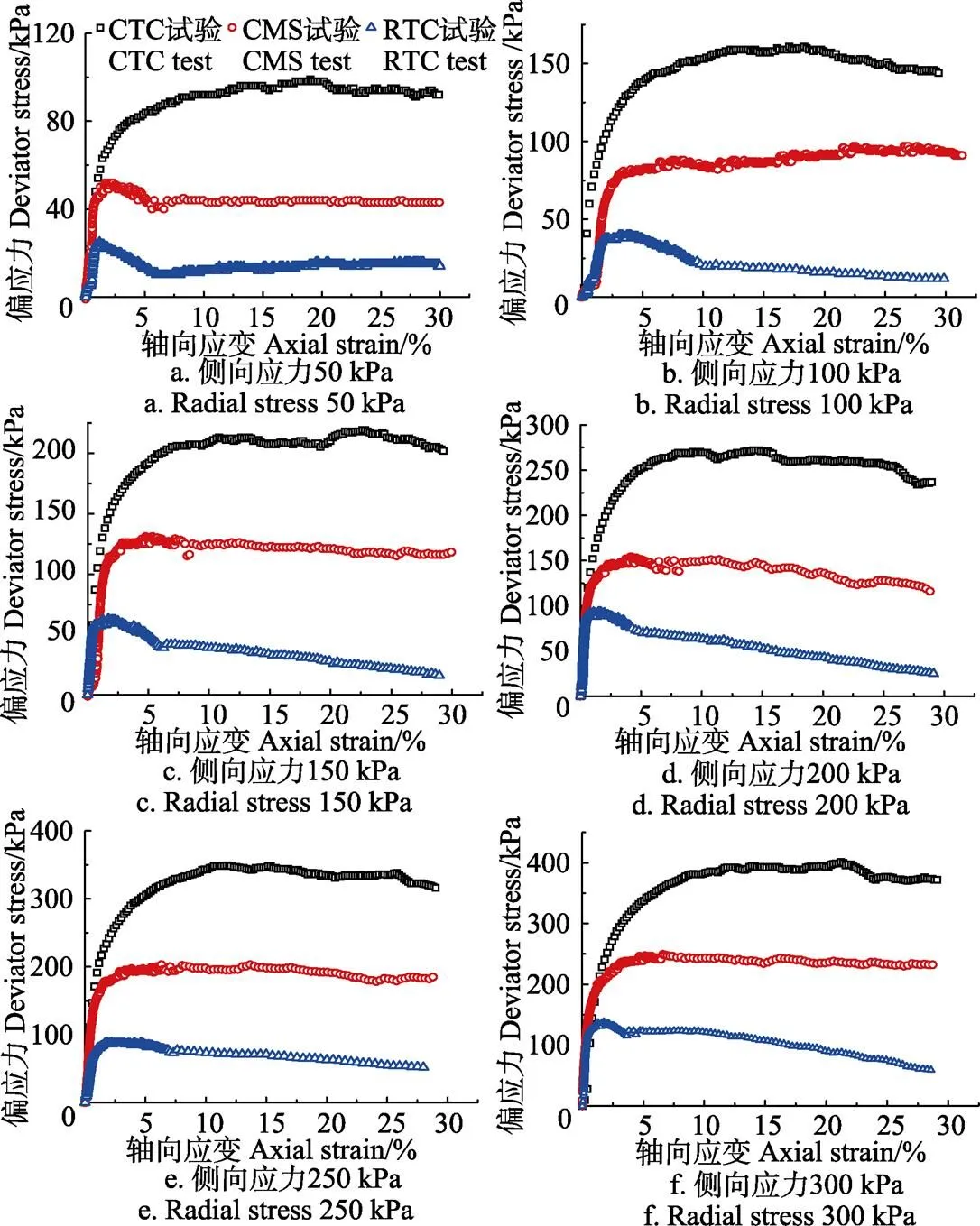
图2 不同侧向应力下小麦粮堆应力路径三轴试验的偏应力与轴向应变关系

三轴试验割线模量=/(MPa)（ε为轴向应变，%）。初始模量E表示小应变（本文取轴向应变0.05%）时的割线模量，散粒体材料在极小的应变下即会产生塑性应变，初始模量近似为粮堆应力应变曲线的弹性模量，是应力应变曲线中模量的最大值[30-31]。50表示偏应力为q/2（q为三轴剪切破坏的偏应力，kPa）时的割线模量。各参量的计算方法如图3所示。

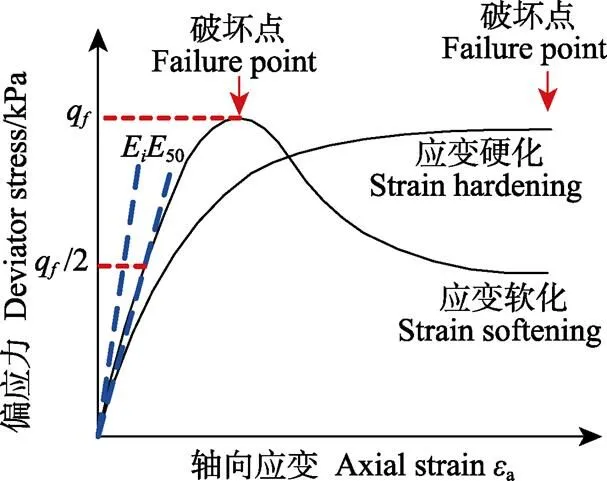
注：qf为三轴剪切破坏的偏应力，kPa，Ei为初始模量，MPa，E50为割线模量，MPa。

各侧向压力和应力路径下初始模量和割线模量的结果，如图4所示，图4纵横坐标均为对数坐标。由图4可知，侧向应力为50至300 kPa时，CTC试验的初始模量介于14.6和51.4 MPa之间，CMS试验的初始模量介于8和34.6 MPa之间，RTC试验的初始模量介于4.1和34.8 MPa之间。侧向应力越大，初始模量越大；相同侧向应力下，CTC试验的初始模量最大，RTC试验的初始模量最小。图4结果表明，在双对数坐标图中，各应力路径试验初始模量均随着侧向应力呈线性增长；即初始模量随着侧向应力呈幂函数增长，表示为：

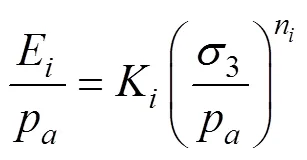
式中p为参考压力（大气压力常数），100 kPa；3为侧向应力，kPa；K和n为模型参数，其中K为参考压力下初始模量，n为双对数坐标中初始模量随着侧向应力的增长速率，是图4双对数坐标轴中直线的斜率。各应力路径试验模型参数K和n结果如表1所示。对于参数K，CTC试验最大，为240.5，RTC试验最小，为79.2，该参数是初始模量E与参考压力p的比值，表示参考压力（大气压100 kPa）下CTC试验的初始模量为24.1 MPa，RTC试验的初始模量为7.9 MPa；参考压力下CTC试验初始模量最大，RTC试验初始模量最小。对于参数n，CTC试验最小，为0.639；RTC试验最大，为1.184；即RTC试验初始模量随着侧向应力增长最快，CTC试验初始模量随着侧向应力增长最慢。

从图4试验结果可见，CTC试验和CMS试验的割线模量50比初始模量发生较大的降低，而RTC试验割线模量50与初始模量较接近。在双对数坐标图中，各应力路径下割线模量50也随着侧向应力呈线性增长；即割线模量50随着侧向应力也呈幂函数增长，表示为：

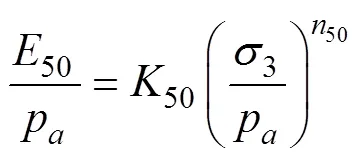
式中K50和n50为模型参数，K50反映了参考压力100 kPa下的割线模量，n50反映了在双对数坐标中割线模量随着侧向应力的增长速率。各应力路径试验模型参数K50和n50的结果见表1。对于参数K50，CTC试验最小，为77.3，RTC试验最大，为90.3，该参数是初始模量E50与参考压力pa的比值，表示参考压力（大气压100 kPa）下CTC试验的初始模量为7.7 MPa，RTC试验的初始模量为9 MPa；参考压力下CTC试验割线模量E50最小，RTC试验割线模量E50最大。对于参数n50，CTC试验最小，为0.719，RTC试验最大，为1.096；即RTC试验割线模量随着侧向应力增长最快，CTC试验割线模量随着侧向应力增长最慢。

表1 小麦粮堆模量模型参数

注：系数K为参考压力下初始模量，无量纲；系数50为参考压力下割线模量，无量纲；系数n为双对数坐标中初始模量随着侧向应力的增长速率，无量纲；系数50为双对数坐标中割线模量随着侧向应力的增长速率，无量纲。

Note: parameterKis initial modulus under reference pressure, dimensionless; parameter50is secant modulus under reference pressure, dimensionless; parameternis increasing rate of initial modulus under logarithmic scale, dimensionless; parameter50is increasing rate of secant modulus under logarithmic scale, dimensionless.

2.1.2 临界状态特性

不同应力路径和侧向应力下，剪切过程中小麦粮堆的偏应力-平均法向应力路径结果如图5所示。由图5可知，本文应力路径试验的轴线应变均达到30%，远大于破坏应变。CTC试验的应力路径沿着偏应力增量与平均法向应力增量比值D/D=3升高至最大偏应力，侧向应力300 kPa时最大偏应力为400.4 kPa；CMS试验的应力路径沿着平均法向应力增量D=0升高至最大偏应力，后随着平均法向应力的微降，偏应力略有降低，侧向应力300 kPa时最大偏应力为244.4 kPa，后略降至232.5 kPa；RTC试验的应力路径沿着D/D=-3/2升高至最大偏应力，后随着平均法向应力的降低，偏应力有较大的降低，侧向应力300 kPa时最大偏应力为136 kPa，后降至60.8 kPa。

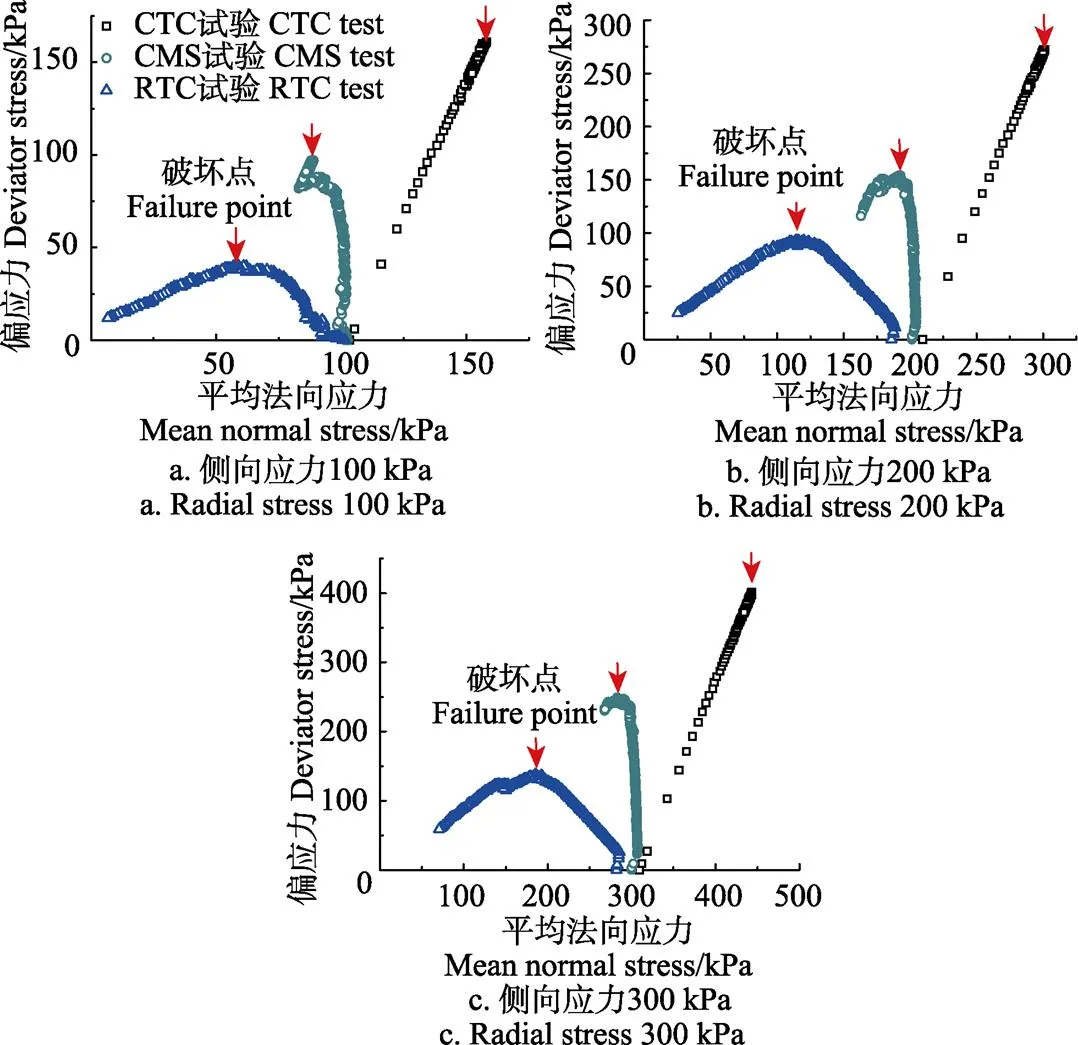
图5 剪切过程中偏应力-平均法向应力路径

各应力路径下偏应力达到峰值后均会有一定的降低，峰值偏应力后不能继续承载，为破坏点，如图5所示。在破坏点之前，偏应力不断增大，在破坏点之后，偏应力不断减小，粮堆中的偏应力不会高于破坏点；在偏应力-平均法向应力（-）平面上粮堆中的应力状态始终位于破坏点之下。

在-平面上，由图5提取不同应力路径（包含CTC、CMS和RTC）和侧向应力（50～300 kPa范围）条件下的破坏点，如图6所示。由图6可见，在不同应力路径和侧向应力条件下，破坏点均落于同一直线上，该直线为小麦粮堆的临界状态线[29]，小麦粮堆临界状态线的斜率为0.976，表明不同条件下破坏点的偏应力与平均法向应力呈正比。在各类应力路径和不同侧向应力下，小麦粮堆在-平面上应力状态均位于临界状态线以内，当达到临界状态线时试样破坏。

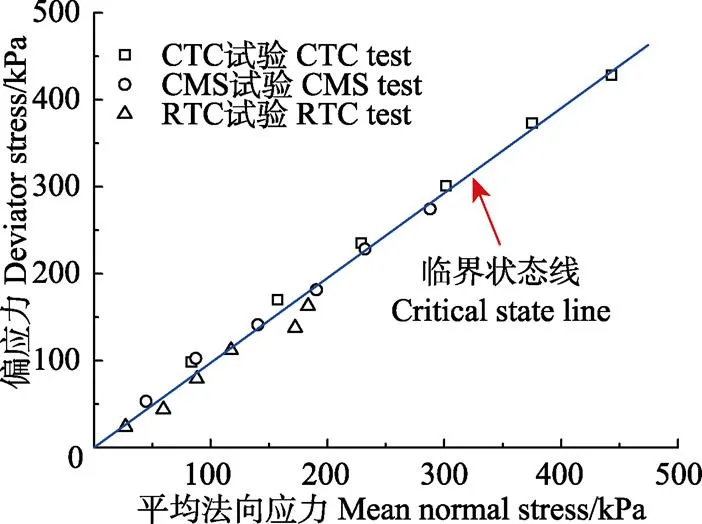
图6 q-p平面上小麦粮堆临界状态线

2.2 应力应变关系参数

2.2.1 峰值强度和残余强度

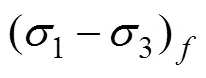
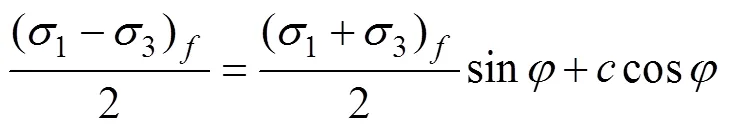
式中为表观黏聚力，kPa；为内摩擦角，（°）；下标表示峰值强度对应的结果。根据公式（3）和图7a得出小麦粮堆在不同应力路径下的表观黏聚力和内摩擦角结果如表2所示，3种应力路径表观黏聚力介于7～34.2 kPa之间，内摩擦角介于34°～47.7°之间。

图2结果显示，在较大轴向应变下，小麦粮堆偏应力趋于一个较低的稳定值，称为残余强度[29]。本文研究表明，小麦粮堆的残余强度也符合莫尔-库伦破坏准则[35]，如图7b所示，表示为：

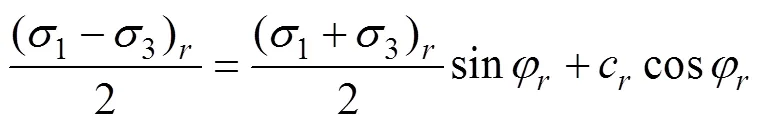
式中为残余偏应力，kPa；为相应的平均应力，kPa；cr为残余表观黏聚力，kPa；φr为残余内摩擦角，（°）；下标r表示残余强度对应的结果。根据公式（4）和图7b得出不同应力路径下小麦粮堆的残余表观黏聚力和残余内摩擦角结果如表2所示，3种应力路径残余表观黏聚力介于11.6～29.4 kPa之间，残余内摩擦角介于29.1°～44.7°之间。

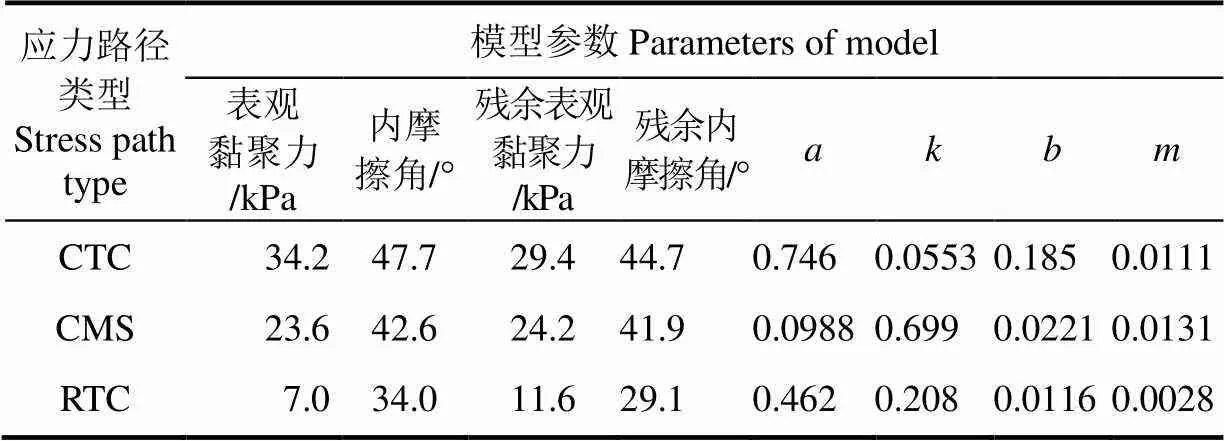
表2 小麦粮堆三次曲线模型参数

2.2.2 峰度系数

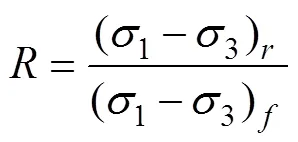
式中a和k为参数，结果如表2所示。

2.2.3 峰值轴向应变

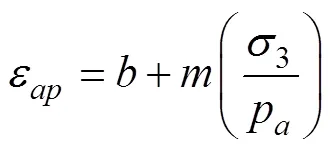
式中b和m为参数，结果如表2所示；pa为大气压力常数，100 kPa。

2.3 应力应变关系模型

2.3.1 修正三次曲线模型

由于岩土体材料的种类繁多，其应力应变特性和破坏规律也较复杂，有多种用于模拟应力应变关系的本构模型[37]。沈珠江三次曲线模型是一种能反映应变软化和塑性破坏等多重特征的模型[36]，且参数易于获取，便于在大型复杂工程中进行数值计算。该模型的应力应变关系为：

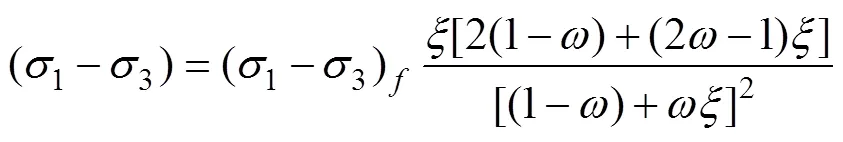
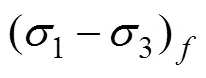
2.3.2 应力应变关系的模拟

本文进行了常规三轴压缩、等压缩和三轴主动压缩3种应力路径试验，试验侧向应力为50、100、150、200、250、300 kPa，覆盖粮堆通常的应力范围[38]。应用本文提出的修正三次曲线模型计算小麦粮堆偏应力应变结果，并与图2中试验结果进行对比，如图10a～10c所示。应用本文计算模型和参数，模拟Zhang等[39]的小麦常规三轴压缩试验结果，如图10d所示。

CTC试验和CMS试验实测值与计算值的相关系数2通常大于0.95，具有较好的相关性。RTC试验实测值与计算值的相关系数2通常大于0.8，图10c中，侧向应力较大的三轴主动压缩试验结果与模型计算结果存在一定的偏差。分析原因如下：三轴主动压缩路径下应力应变曲线的应变软化现象明显（偏应力达到峰值后下降），尤其是侧向应力为300 kPa时，偏应力在峰值后急剧降低，剪切面上颗粒错动和颗粒位置变化更难均匀地调整，受到两端端部和橡皮膜的约束，试样更不易产生均匀的变形，形成鼓胀变形，导致偏应力在轴向应变约4%（偏应力急剧下降点）后，略有上升后，再出现降低，引起模型计算结果与试验结果在峰值偏应力后产生差异[40]。

由图10可知修正三次曲线模型具有如下特点：模型计算结果总体可较好地反映粮堆不同应力路径的应力应变关系；该模型可较好地反映小麦粮堆的应变硬化和应变软化力学特性；能较准确地模拟各应力路径下粮堆的峰值强度和残余强度。

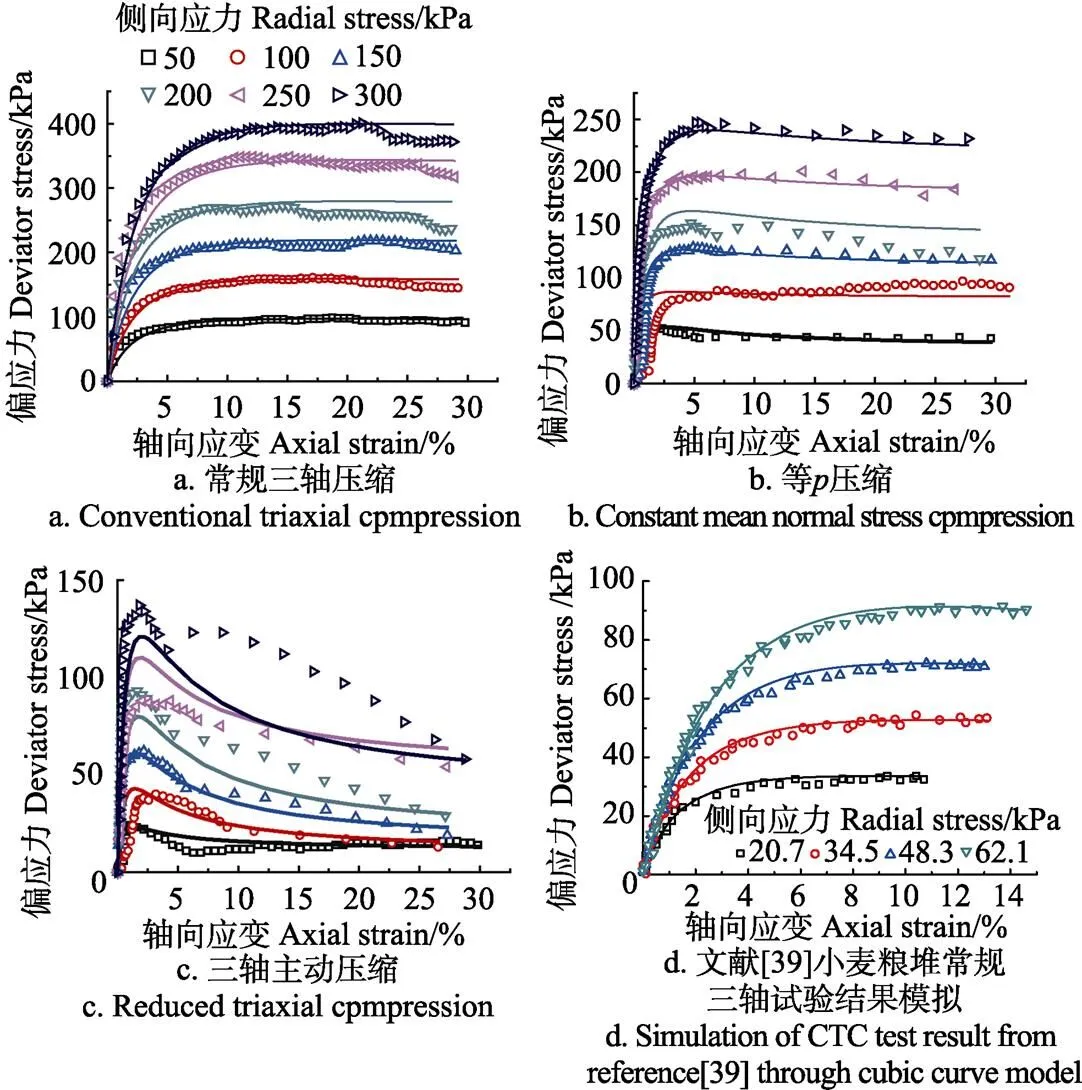
注：图中点为试验结果，线为模型计算结果。

3 结 论

本文针对粮仓装卸粮过程中存在的复杂应力路径问题，利用三轴应力路径试验，研究了不同路径、侧向应力下粮堆的模量规律和临界状态特性，建立了新的小麦粮堆应力应变关系模型，并通过应力路径三轴试验和文献试验结果，对模型进行了验证，得到以下主要结论：

1）相同侧向应力下，CTC试验的初始模量最大，RTC试验的初始模量最小。各应力路径下初始模量、割线模量50均随着侧向应力呈幂函数增长。CTC、CMS试验的割线模量50与初始模量相比发生较大的降低，而RTC试验割线模量50与初始模量相比没有明显降低。参考压力（大气压力）下，CTC试验初始模量最大，为24.1 MPa，RTC试验结果最小，为7.9 MPa；CTC试验初始模量随着侧向应力增长最慢，RTC试验结果增长最快。参考压力下CTC试验割线模量50最小，为7.7 MPa，RTC试验结果最大，为9 MPa；CTC试验割线模量随着侧向应力增长最慢，RTC试验结果增长最快。

2）不同应力路径和侧向应力条件下，粮堆三轴应力路径试验在破坏前的应力状态位于临界状态线以内；破坏点均落于同一临界状态线上。小麦粮堆临界状态线为直线，本文试验临界状态应力比为0.976。

3）修正岩土体应力应变关系的三次曲线模型，提出适用于小麦粮堆强度、峰度系数和峰值轴向应变的新计算方法，得出了适用于模拟粮仓内小麦粮堆应力应变关系的新模型。模型包括表观黏聚力、内摩擦角、残余表观黏聚力、残余内摩擦角、、、、共8个参数，并可通过三轴试验得出。

4）通过修正的三次曲线模型计算粮仓内压力范围内的应力路径结果，并与试验结果和文献试验结果进行对比，表明计算模型可模拟复杂应力路径下粮堆应变硬化和软化、强度特性、偏应力应变关系等力学特性。

[1] Dogangun A, Karaca Z. Cause of damage and failures in silo structures[J]. Journal of Performance of Constructed Facilities, ASCE, 2015, 23(2): 65－71.

[2] Song C Y, Teng J G. Buckling of circular steel silos subject to code-specified eccentric discharge pressures[J]. Engineering Structures, 2003, 25(11): 1397－1417.

[3] Rotter J M, Sadowski A J. Cylindrical shell bending theory for orthotropic shells under general axisymmetric pressure distributions[J]. Engineering Structures, 2012, 42(12): 258－265.

[4] Sadowski A J, Rotter J M. Study of buckling in steel silos under eccentric discharge flows of stored solids[J]. Journal of Engineering Mechanics, ASCE, 2010, 136(6): 769－776.

[5] Sadowski A J, Rotter J M. Buckling in eccentrically discharged silos and the assumed pressure distribution[J]. Journal of Engineering Mechanics, ASCE, 2013, 139(7): 858－867.

[6] Ayuga F, Guaita M, Aguado P J, Couto A. Discharge and the eccentricity of the hopper influence on the silo wall pressures[J]. Journal of Engineering Mechanics, ASCE, 2001, 127(10): 1067－1074.

[7] 程绪铎. 筒仓中粮食卸载动压力的研究与进展[J]. 粮食储藏，2008，37(5)：20－24. Cheng Xuduo. Research and advance of dynamic pressure in silo during discharge[J]. Grain storage, 2008, 37(5): 20－24. (in Chinese with English abstract)

[8] Moya M, Ayuga F, Guaita M, et al. Mechanical properties of granular agricultural materials [J]. Transactions of the Asae, 2002, 45(5): 1569－1577.

[9] Afzalinia S, Roberge M. Physical and mechanical properties of selected forage materials [J]. Canadian Biosystems Engineering, 2007, 49(2): 23－27.

[10] 曾长女，冯伟娜. 小麦强度特性的三轴试验研究[J]. 中国粮油学报，2015，30(5)：96－101. Zeng Changnü, Feng Weina. Strength properties of wheat in triaxial tests[J]. Journal of the Chinese Cereals and Oils Association, 2015, 30(5): 96－101. (in Chinese with English abstract)

[11] 曾长女，于航. 基于线性接触模型的小麦三轴试验细观模拟[J]. 河南工业大学学报，2015，36(2)：66－70. Zeng Changnü, Yu Hang. Meso-simulation of triaxial test of wheat based on linear contact model[J]. Journal of Henan University of Technology, 2015, 36(2): 66－70. (in Chinese with English abstract)

[12] 许启铿，陈家豪，王录民. 小麦力学参数的三轴压缩试验研究[J]. 河南工业大学学报，2015，36(5)：101－105. Xu Qikeng, Chen Jiahao, Wang Lumin. Mechanical properties of wheat in triaxial compression tests[J]. Journal of Henan University of Technology, 2015, 36(5): 101－105. (in Chinese with English abstract)

[13] 陈家豪，韩阳，任杰，等. 小麦堆压缩模量的三轴试验研究[J]. 河南工业大学学报，2016，37(1)：23－28. Chen Jiahao, Han Yang, Ren Jie, et al. Research on triaxial tests on compression modulus of wheat piles[J]. Journal of Henan University of Technology, 2016, 37(1): 23－28. (in Chinese with English abstract)

[14] Stasiak M, Molenda M, Horabik J. Determination of modulus of elasticity of cereals and rapeseeds using acoustic method [J]. Journal of Food Engineering, 2007, 82(1): 51-57.

[15] 程绪铎，高梦瑶，冯家畅，等. 预测平房仓中小麦密度分布与储藏质量的模型[J]. 中国粮油学报，2017，32(3)：96－102. Cheng Xuduo, Gao Mengyao, Feng Jiachang, et al. Model of density distribution and storage quality of wheat in a horizontal warehouse[J]. Journal of the Chinese Cereals and Oils Association, 2017, 32(3): 96－102. (in Chinese with English abstract)

[16] 冯家畅，程绪铎，杜小翠，等. 大豆堆压缩密度与体变模量研究[J]. 中国粮油学报，2016，31(12)：112－117. Feng Jiachang, Cheng Xuduo, Du Xiaocui, et al. Compressive density and bulk modulus of soybean [J]. Journal of the Chinese Cereals and Oils Association, 2016, 31(12): 112－117. (in Chinese with English abstract)

[17] 程绪铎，杜小翠，高梦瑶，等. 玉米堆压缩特性的实验研究[J]. 粮食储藏，2015，44(4)：10－15. Cheng Xuduo, Du Xiaocui, Gao Mengyao, et al. Study on compression properties of corn heap [J]. Grain Storage, 2015, 44(4): 10－15. (in Chinese with English abstract)

[18] 程绪铎，严晓婕，徐鑫. 稻谷堆的压缩密度与体变模量的测定与分析[J]. 中国粮油学报，2014，29(8)：101－105. Cheng Xuduo, Yan Xiaojie, Xu Xin. The measurement and analysis on compressive density and bulk stain modulus of paddy pile [J]. Journal of the Chinese Cereals and Oils Association, 2014, 29(8): 101－105. (in Chinese with English abstract)

[19] Cheng X, Zhang Q, Yan X, et al. Compressibility and equivalent bulk modulus of shelled corn [J]. Biosystems Engineering, 2015, 140: 91-97.

[20] 蒋敏敏，郭祝辉. 竖向压力和剪切速率对小麦直剪强度及剪胀特性的影响[J]. 农业工程学报，2017，33(6)：275－280. Jiang Minmin, Guo Zhuhui. Effects of vertical pressure and shear velocity on direct shear strength and dilatancy properties of wheat heap element [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(6): 275－280. (in Chinese with English abstract)

[21] Nielsen J. Pressures from flowing granular solid in silos[J]. Philosophical Transactions Mathematical Physical & Engineering Sciences. 1998, 356(1747): 2667－2684.

[22] 姜勇. 利用Duncan-Chang模型分析钢板仓壁静压力[J]. 青岛大学学报，2001，16(3)：28－32. Jiang Yong. Analysis of static pressures on steel silo walls by the Duncan-Chang’s nonlinear elastic model[J]. Journal of Qingdao University, 2001, 16(3): 28－32. (in Chinese with English abstract)

[23] Ayuga F, Guaita M, Aguado P J. Static and dynamic silo loads using finite element models. Journal of Agricultural Engineering Research, 2001, 127(10): 1067-1074.

[24] 何世秀，韩高升，庄心善，等. 基坑开挖卸荷土体变形的试验研究[J]. 岩土力学，2003，24(1)：17－20. He Shixiu, Han Gaosheng, Zhuang Xinshan, et al. Experimental researches on unloading deformation of clay in excavation of foundation pit [J]. Rock and Soil Mechanics, 2003, 24(1): 17－20. (in Chinese with English abstract)

[25] 应宏伟，李晶，谢新宇，等. 考虑主应力轴旋转的基坑开挖应力路径研究[J]. 岩土力学，2012，33(4)：1013－1017. Ying Hongwei, Li Jing, Xie Xinyu, et al. Research on stress path during excavation considering rotation of principal stress axis [J]. Rock and Soil Mechanics, 2012, 33(4): 1013－1017. (in Chinese with English abstract)

[26] 张文慧，王保田，张福海. 应力路径对基坑工程变形的影响[J]. 岩土力学，2004，25(6)：964－966.Zhang Wenhui, Wang Baotian, Zhang Fuhai. Influence of stress paths and consolidation stress ratios on soil’s deformation characteristics [J]. Rock and Soil Mechanics, 2004, 25(6): 964－966. (in Chinese with English abstract)

[27] 周葆春. 应力路径对重塑黏土有效抗剪强度参数的影响[J]. 华中科技大学学报，2007，35(12)：83－86. Zhou Baochun. Influence of stress path on effective shear strength parameters of reshaped clay[J]. Journal of Huazhong University of science and technology, 2007, 35(12): 83－86. (in Chinese with English abstract)

[28] GB/T 50123-1999，土工试验方法标准[S]． GB/T 50123-1999，Stand for soil test method[S].

[29] 殷宗泽．土工原理[M]．北京：中国水利水电出版社，2007．

[30] Yasuhara K, Murakami S, Song B W, et al. Postcyclic degradation of strength and stiffness for low plasticity silt [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2003, 129(8): 756-769.

[31] Lee J, Salgado R, Carraro J A H. Stiffness degradation and shear strength of silty sands [J]. Canadian Geotechnical Journal, 2004, 41(5): 831-843.

[32] 龚晓南. 软黏土地基土体抗剪强度若干问题[J]. 岩土工程学报，2011，33(10)：1596－1600. Gong Xiaonan. Some problems concerning shear strength of soil in soft clay ground [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1596－1600. (in Chinese with English abstract)

[33] 孔纲强，刘璐，刘汉龙，等. 玻璃砂透明土与标准砂土强度特性对比三轴试验[J]. 建筑材料学报，2014，17(2)：250－255. Kong Gangqiang, Liu Lu, Liu Hanlong, et al. Comparative analysis of the strength characteristics of transparent glass sand and standard sand [J]. Journal of Building Materials, 2014, 17(2): 250－255. (in Chinese with English abstract)

[34] 刘萌成，高玉峰，刘汉龙. 应力路径条件下堆石料剪切特性大型三轴试验研究[J]. 岩石力学与工程学报，2008，27(1)：176－186. Liu Mengcheng, Gao Yufeng, Liu Hanlong. Study on shear behaviors of rockfill in large-scale triaxial tests under different stress paths[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 176－186. (in Chinese with English abstract)

[35] 王顺，项伟，崔德山，等. 不同环剪方式下滑带土残余强度试验研究[J]. 岩土力学，2012，33(10)：2967－2972. Wang Shun, Xiang Wei, Cui Deshan, et al. Study of residual strength of slide zone soil under different ring-shear tests [J]. Rock and Soil Mechanics, 2012, 33(10): 2967－2972. (in Chinese with English abstract)

[36] 沈珠江. 考虑剪胀性的土和石料的非线性应力应变模式[J]. 水利水运科学研究，1986(4)：1－14. Shen Zhujiang. A nonlinear dilatant stress-strain model for soils and rock materials [J]. Hydro-Science and Engineering, 1986(4): 1－14. (in Chinese with English abstract)

[37] 王丽琴，鹿忠刚，邵生俊. 岩土体复合幂-指数非线性模型[J]. 岩石力学与工程学报，2017，36(5)：1269－1278. Wang Liqin, Lu Zhonggang, Shao Shengjun. A composite power exponential nonlinear model of rock and soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(5): 1269－1278. (in Chinese with English abstract)

[38] Cheng X, Zhang Q, Shi C, et al. Model for the prediction of grain density and pressure distribution in hopper-bottom silos [J]. Biosystems Engineering, 2017, 163: 159-166.

[39] Zhang Q, Puri V M, Manbeck H B. Determination of Elastoplastic Constitutive Parameters for Wheat En Masse[J]. Transactions of the ASAE, 1986, 29(6): 1739－1746.

[40] 陆晓平，孙明辉，陈浩锋，等. 粗粒土三轴试样端部约束影响研究[J]. 岩土工程学报，2017，39(增刊1)：236－240. Lu Xiaoping, Sun Minghui, Chen Haofeng, et al. Effects of end restraint in triaxial tests on coarse-grained soil [J]. Chinese Journal of Geotechnical Engineering, 2017, 39(S1): 236－240. (in Chinese with English abstract)

Mechanical properties and stress strain model for bulk wheat based on stress path test

Jiang Minmin1,2, Chen Guixiang1,2

(1.450001,; 2.450001,)

Total amount of stored grain in China is about 200 million tons, which is of great importance to ensure the quality and safety of grain during storage period, and to modernization of agriculture engineering. When a storage cycle is ended, grain will be discharged from bins, and then loaded in for another storage cycle. Vertical stress increases in loading process, while decreases in discharging process, and different stress path will be generated in the bulk grain, resulting in complicated pressure and frictional force on bin wall, which will cause crack, failure or even overturn of bin structures. It is vital to study stress strain relation and strength properties of bulk grain under different stress paths. Geotechnical constitutive models have been used in grain bin simulation, however, the feasibility of these models for bulk grain has not been validated. In this study, stress path triaxial test was utilized to simulate complicated load path in grain bins. Wheat purchased from grain depot in Zhengzhou City, Henan Province was used in this study. Specimen had water content of 10.9%, bulk density of 0.85 g/cm3, diameter of 61.8 mm and height of 125 mm, the average axial length of wheat kernel was 4.5 mm, and the ratio of specimen diameter to kernel axial length was 13.7, which was larger than the minimum specified ratio for triaxial test. Three types of stress paths were investigated in this study: conventional triaxial compression (CTC), constant mean normal stress compression (CMS), and reduced triaxial compression (RTC). In CTC test, radial stress was set as constant, while axial stress increased simultaneously; in CMS test, radial stress decreased, while axial stress increased simultaneously to keep mean normal stress constant; in RTC test, axial stress was set as constant, and radial stress decreased simultaneously. Stress path triaxial test procedure was as follows: After bulk wheat specimen was mounted on triaxial apparatus, isotropic stress was applied from 0 to prescribed value (50, 100, 150, 200, 250, 300 kPa); then CTC, CMS or RTC stress path was applied on specimen, and stress strain result was recorded until axial strain reached 30%. Initial modulus, secant modulus and critical state properties were determined from stress strain curve, strength and stress strain parameters were determined, and finally new model was proposed to depict stress strain relation for bulk wheat under different stress paths. Test results show that, under the same radial stress, CTC test has the largest initial modulus, and RTC test has the lowest value. Under all stress paths, initial modulus and secant modulus are found to be in a power function growth with the ascent of radial stress. In CTC test and CMS test, secant modulus is significantly lower than initial modulus; while in RTC test, secant modulus is not significantly reduced compared with initial modulus. Under reference pressure (atmospheric pressure), CTC test has the largest initial modulus of 24.1 MPa, and RTC test has the lowest value of 7.9 MPa; while initial modulus of RTC test has the largest increasing rate, CTC test has the lowest increasing rate. Under reference pressure, CTC test has the lowest secant modulus of 7.7 MPa, and RTC test has the largest value of 9 MPa; secant modulus of RTC test has the largest increasing rate, and CTC test has the lowest increasing rate. Deviator stress increased during shearing process, and specimen failed at the peak point on-(deviator stress - mean normal stress) plane. Under all stress path and radial stress situations, failure point fell on the same critical state line. Critical state line for bulk wheat has straight line form, and critical state stress ratio is 0.976. New modified cubic curve model for bulk wheat grain under different stress path conditions was proposed. In the model, strength conforms to Mohr-Coulomb failure criterion; crest reduction coefficient has linear relation with residual strength ratio; peak axial strain has linear relation with radial stress. Model parameters comprised apparent cohesion, internal friction angle, residual apparent cohesion, residual internal friction angle, parameterandfor crest reduction coefficient, and parameterandfor peak axial strain. Calculated results show that the proposed model can simulate the results of all stress paths under different confining stress levels. The model can reflect strain softening and strain hardening properties of bulk wheat; peak shear strength and residual shear strength can be determined; and the simulated stress and strain curve coincide well with the test results. The result of this paper provides more accurate parameters for grain bin load calculation considering the stress path conditions, and the new model can be used to estimate stress and deformation of bulk wheat, and to improve the designing method of grain bins.

stress; strain; models; bulk wheat; stress path triaxial test

蒋敏敏，陈桂香. 基于应力路径试验的小麦粮堆力学特性和应力应变关系模型[J]. 农业工程学报，2018，34(7)：280－287. doi：10.11975/j.issn.1002-6819.2018.07.036 http://www.tcsae.org

Jiang Minmin, Chen Guixiang. Mechanical properties and stress strain model for bulk wheat based on stress path test[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 280－287. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.07.036 http://www.tcsae.org

2017-11-06

2018-02-22

国家自然科学基金项目（51408197）；粮食公益性行业科研专项（201513001）；河南省科技攻关项目（162102210188）；河南省属高校基本科研业务费专项资金（2015RCJH16）

蒋敏敏，男，江苏盐城人，博士，副教授，主要从事粮食仓储结构研究。Email：jiangmmhaut@126.com

10.11975/j.issn.1002-6819.2018.07.036

TS210

A

1002-6819(2018)-07-0280-08