圆柱型正交各向异性圆板的自由振动分析

李秋红，刘广明，薛开，王久法，王平

(哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001)

近年来，随着科学与技术的进步，各种工程结构逐渐向着轻量化、高强度方向发展。圆柱型正交各向异性圆板结构由于其特有的几何特点和材料性能在航空航天、海洋工程和机械工程中得到了广泛的应用。由于板结构极易引起共振现象造成结构的破坏，因此，对于圆柱型正交各向异性圆板的振动分析越来越引起人们的注意。同时，深入开展圆柱型正交各向异性圆板结构的动力学特性研究具有十分重要的理论意义和工程应用价值。

Zhou等［1］利用哈密顿原理分析和研究了各向同性圆板和环板的自由振动;Viswanathan等［2］采用多项式样条函数逼近正交各向异性圆板振动的位移函数，研究了层合圆环板的自由振动;Lin等［3］采用有限元法，基于八节点等参单元分析了圆柱型正交各向异性层合圆板和环板的自由振动;Hua等［4］采用板刚度识别法试验预测了圆柱型正交各向异性圆板的振动数据。此外，还有许多学者采用满足不同边界条件的边界特征多项式［5］，基于能量原理［6-7］对该类问题进行了分析，如文献［8-9］采用正交多项式分析了弹性地基上变厚度圆柱型正交各向异性圆板和环板的自由振动;文献［10］基于参数多项式分析了圆柱型正交各向异性圆板的自由振动。综上所述，目前的研究对于圆柱型正交各向异性圆板在边界条件的处理上较为单一，大部分文献仅仅涉及复杂边界条件的简支、固支边界，而且同种求解方法面对不同的边界条件时需要重新进行公式推导。因此，这给圆柱型正交异性圆板结构的工程设计和动力学特性分析带来了不便。

近年来，Li等［11-14］提出了一种二维改进的Fourier级数方法，进行了弹性约束边界条件下矩形板结构的振动分析。通过将位移函数表示为标准的Fourier级数和辅助多项式的形式，有效地解决了位移函数在边界处的连续性。本文将上述改进级数方法扩展至圆板结构的振动分析，提出了一种改进的Fourier-Bessel级数方法。

1 圆柱型正交各向异性圆板结构的数学模型

1.1 模型的描述

在极坐标系Orθ下建立的半径为a、厚度为h的圆柱型正交各向异性薄圆板结构的数学模型如图1所示，假定材料的第一弹性主方向与极轴r方向一致，材料的第二弹性主方向与极角θ方向一致。圆板结构的边界条件利用边界上均匀分布的横向位移弹簧和扭转约束弹簧来模拟。所有的经典边界条件(固支、简支和自由)都可以通过设置弹簧的刚度为零或无穷大来获得，比如令横向位移弹簧刚度为无穷大和扭转约束弹簧刚度为零来获得简支边界条件。

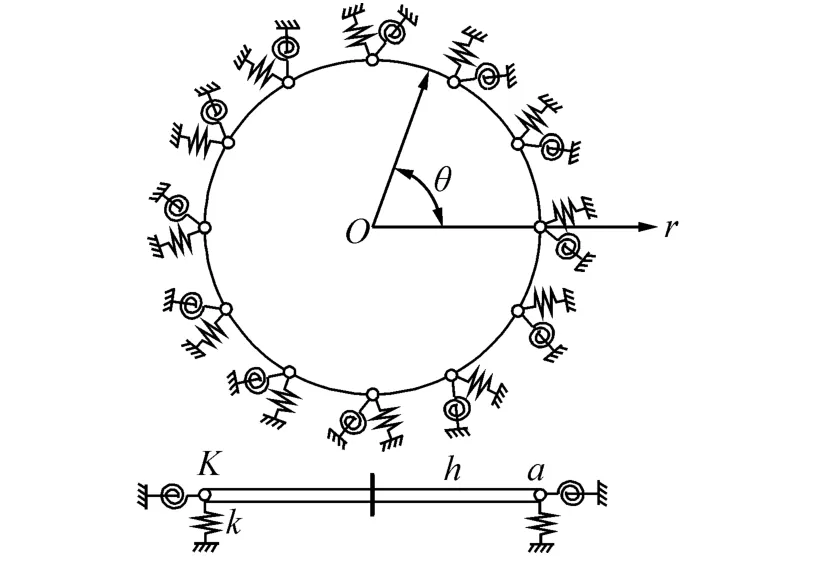
图1 圆柱型正交各向异性圆板结构的数学模型Fig.1 Mathematical model of cylindrical orthotropiccircular plates structure

根据复合材料力学理论，圆柱型正交各向异性圆板结构自由振动的微分控制方程［15］为

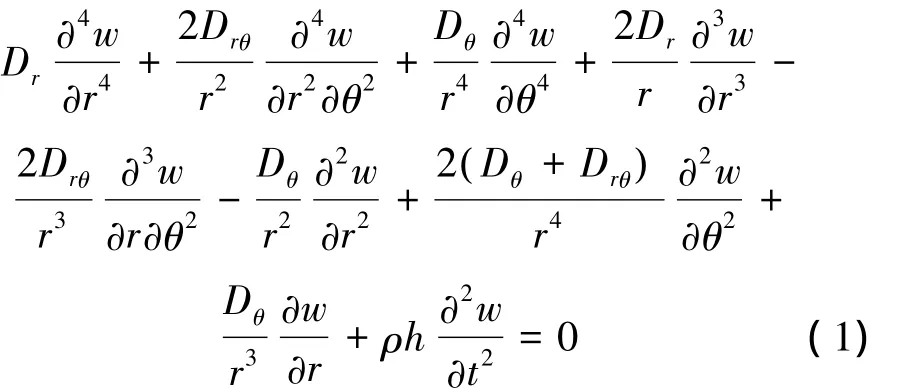
式中:ρ为圆板的密度，Dr、Dθ和 Drθ均为圆板的刚度，表达式分别为

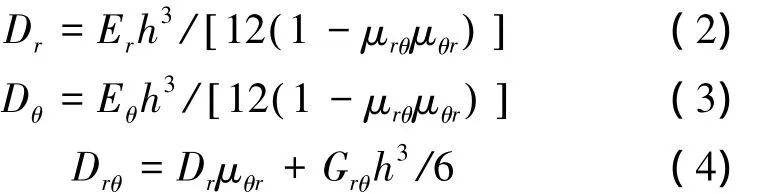
式中:Er、Eθ为圆柱型正交各向异性圆板第一、第二弹性主方向的杨氏模量;μrθ、μθr为对应弹性主方向的泊松比;Grθ为剪切弹性模量。在圆柱型正交各向异性材料中，杨氏模量与泊松比之间有如下关系:

圆柱型正交各向异性圆板结构自由振动的微分控制方程(1)为典型的变系数四阶偏微分方程，同时考虑得到板结构的边界条件，因此在方程的求解上将变得十分困难，为此本文采用能量原理中的Rayleigh-Ritz方法进行圆板结构的振动分析。

针对图1所示的圆柱型正交各向异性圆板结构，系统的总能量可以表示为

式中:U为板结构的弯曲应变能，V为边界上弹簧的总势能，T为板结构的动能，表达式分别为

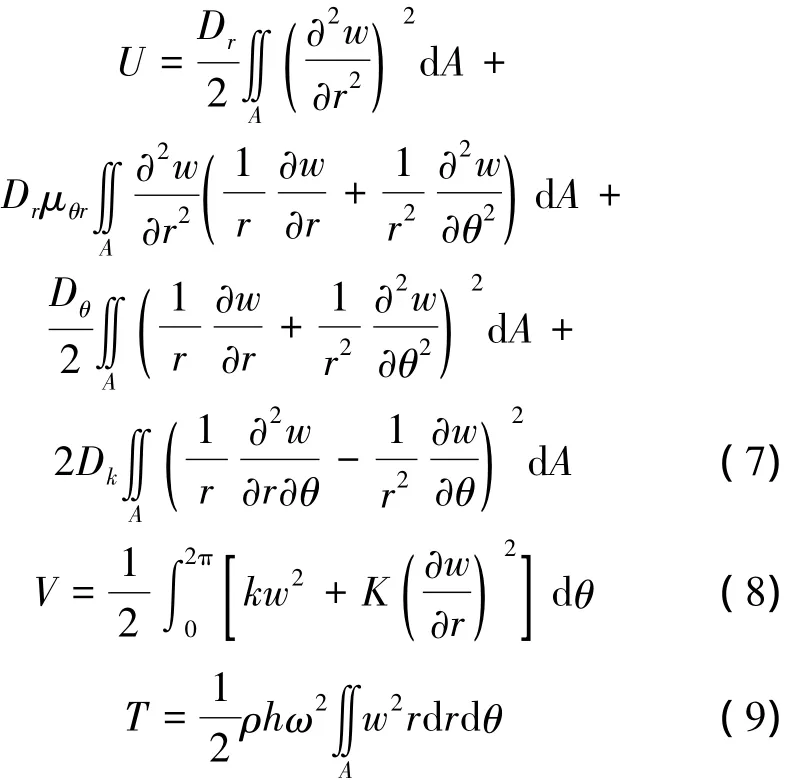
式中:k和K分别为横向位移弹簧和扭转约束弹簧的刚度系数。

1.2 位移函数的表达

在极坐标系下，将圆柱型正交各向异性圆板结构的振动位移函数表示为径向和轴向可分离的形式:

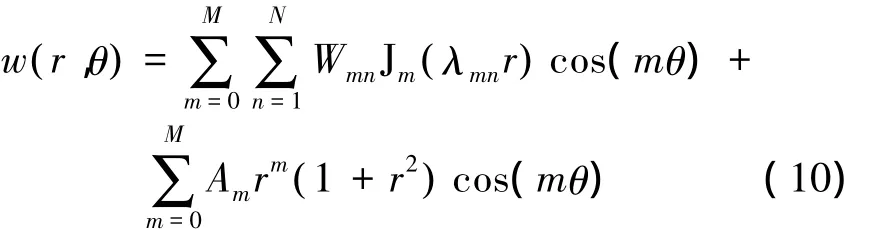
式中:Wmn、Am分别为未知的Fourier-Bessel级数和辅助多项式的系数;Jm(x)为m阶Bessel函数;λmn为Jm(x)=0的第n个正根。表达式中第2项辅助多项式函数是为了改善振动位移函数在圆板边界处的连续性、提高方法的数值收敛性问题而引入的。

1.3 模型的计算

根据Rayleigh-Ritz方法，将圆柱型正交各向异性圆板结构的振动位移函数表达式代入能量表达式(6)～(9)中，对未知的系数 Wmn、Am求极值，可以得到圆柱型正交各向异性圆板自由振动的矩阵方程:

式中:A为未知的系数向量，K=Kp+Ks为总刚度矩阵，M为总质量矩阵，表达式分别如下:

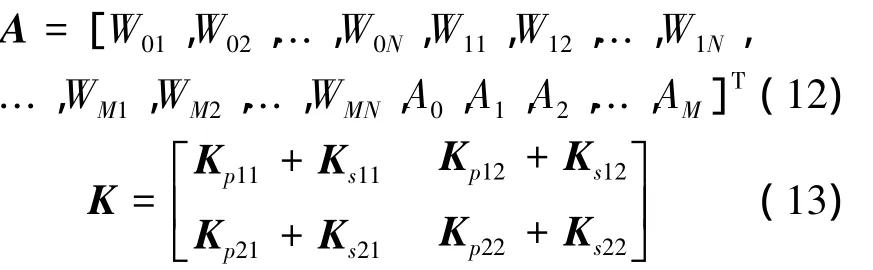
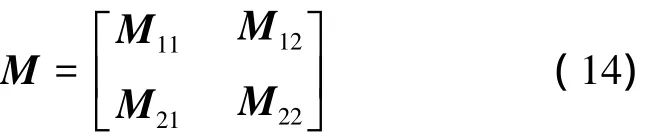
式中:Kp为由板弯曲应变能获得的刚度矩阵，Ks为由边界上弹簧总势能获得的刚度矩阵，其各矩阵的子矩阵元素表达式分别如下

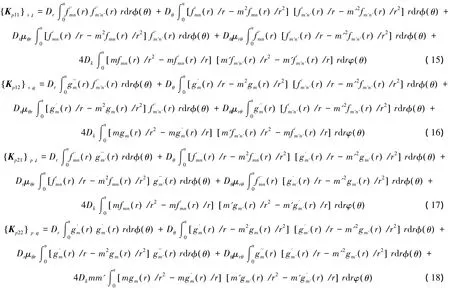
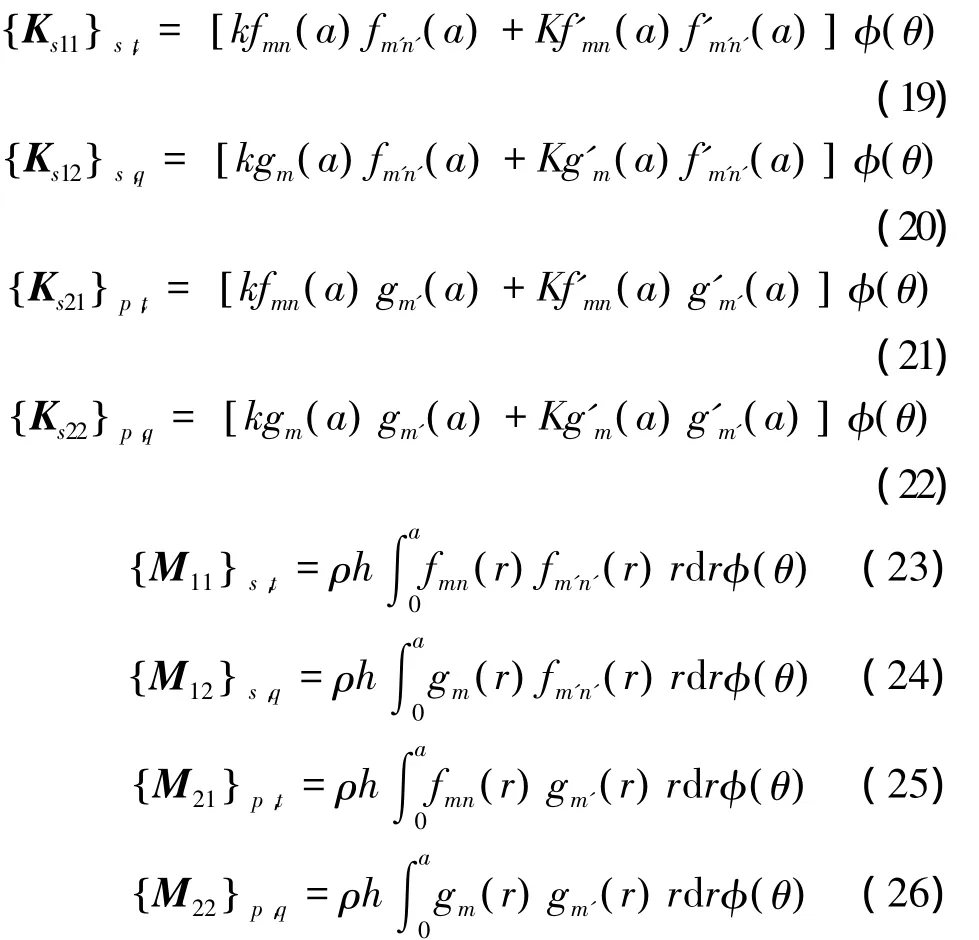
式中:fmn(r)=Jm(λmnr)，gm(r)=rm(1+r2)，其中m'=0，1，..，M，n'=1，2，..，N，s=N(M+1)，t=N(M+1)，p=M+1，q=M+1;M和N表示方法的截断数，其大小根据要求的计算精度进行取值;φ(θ)和φ(θ)的表达式分别为

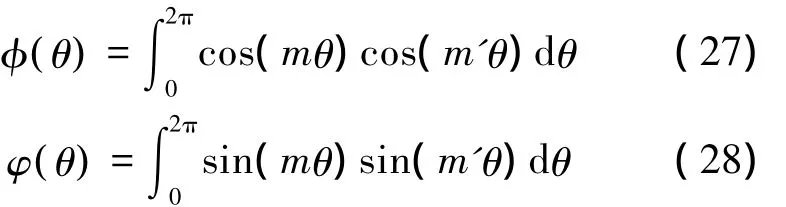
方程(11)为典型的线性齐次方程组，由于未知系数向量A不全为零，则必有方程的系数行列式为零，即

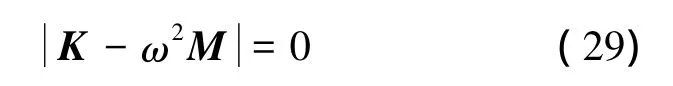
方程(29)为典型的矩阵特征值问题，通过求解矩阵特征值和特征向量，即可以得到圆板的自由振动频率和相应的未知系数向量A，将未知系数向量A代入位移函数(10)中就可以获得相应的振动频率对应的模态振型。

2 数值算例

为验证方法的正确性，进行以下数值算例研究。考虑到均匀各向同性材料圆板作为圆柱型正交各向异性圆板的特例。首先考虑各向同性圆板结构的自由振动，然后再对圆柱型正交各向异性圆板的自由振动进行分析。同时本方法建立的结构模型在对边界条件的处理上，具有很强的通用性，可以通过设置不同边界条件下弹簧的刚度系数进行数值模拟。

2.1 均匀各向同性圆板

在均匀各向同性材料时，根据前文的理论分析，有 E=Er=Eθ、μ=μrθ=μθr、G=Grθ=E/(2(1+μ))。假定圆板的结构及材料参数如下:半径a=1 m，厚度h=0.01 m，板的密度 ρ=7 800 kg/m3，弹性模量 E=206 GPa，泊松比 μ=0.3。考虑不同边界条件下，均匀各向同性圆板自由振动的前5阶固有频率，并与有限元软件Ansys仿真分析结果进行对比，如表1所示。在有限元仿真分析中为了提高数值精度，选择8节点Shell单元，划分单元4 430个、节点13 487个。为了衡量结果的数值准确性，表1中还给出了对应固有频率的相对误差。通过表1可以看到2种方法的最大相对误差不超过0.270 8%，即本文方法计算结果与有限元仿真分析结果几乎相一致。

为了进一步验证本方法获得振型的正确性，图2中分别给出了本文方法和有限元软件Ansys仿真分析获得的自由边界条件下圆板前5阶振动频率对应的模态振型。通过图2中2种方法获得的阵型图对比，清晰的表明圆板振动的节圆与节线分布形式一致，这也进一步验证了本方法的正确性。

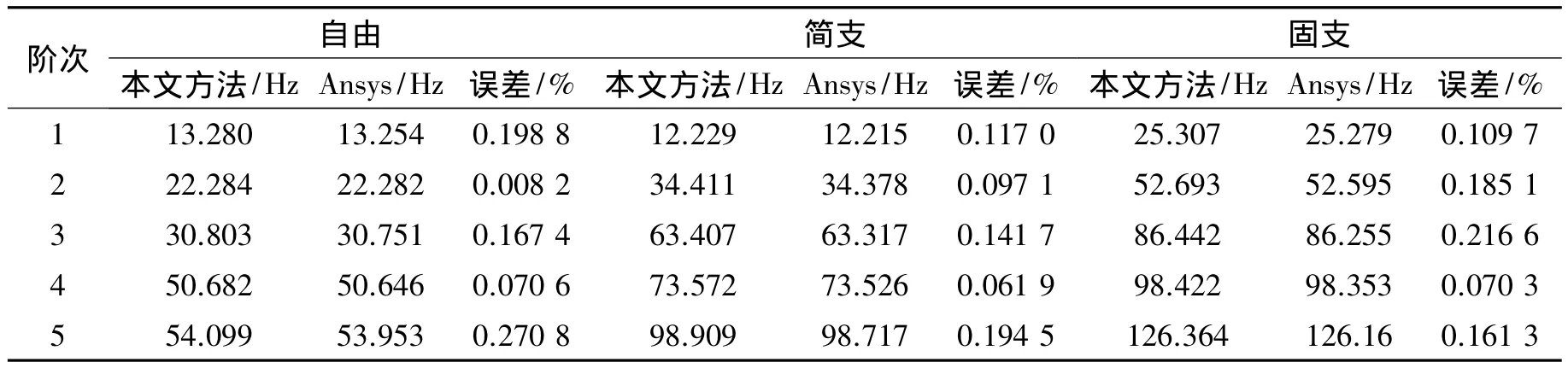
表1 不同边界条件下圆板的前5阶固有频率Table 1 The first five natural frequencies for circular plates with different boundary conditions

图2 自由边界圆板前5阶振型Fig.2 The first five mode shapes for free circular plates

2.2 圆柱型正交各向异性圆板

考虑圆柱型正交各向异性圆板的自由振动分析。为了方便与文献结果进行对比，以下数值算例按照文献［4］中设置材料模型:a=75 mm，h=1.93 mm，ρ=1 640 kg/m3，μrθ=0.3，Er=16 GPa，Eθ=10 GPa，Grθ=4 GPa。

表2中给出了周边自由时，圆柱型正交各向异性圆板自由振动的前5阶固有频率，作为对照给出了文献［4］利用板刚度识别试验和文献［10］利用能量法获得的结果，同时给出了本方法相对于文献［4］中实验结果的相对误差。通过表2可以看到3种方法获得的计算结果相差不大;本方法与文献［4］实验结果的最大相对误差不超过0.362 8%，即文献的实验结果与本方法计算结果相一致，进一步说明了本方法理论分析与试验数据的相吻合。

表3给出了本方法在周边简支及固支时，圆柱型正交各向异性圆板自由振动的前5阶固有频率，并给出了利用有限元软件Ansys仿真分析结果，同时也给出了两者的相对误差。通过表3中相对误差的分析，最大相对误差不超过0.673 0%，两者计算结果也几乎一致。阶次 1 2 3 4 5

表2 自由边界条件下圆板的前5阶固有频率Table 2 The first five natural frequencies for circular plates with free boundary conditions

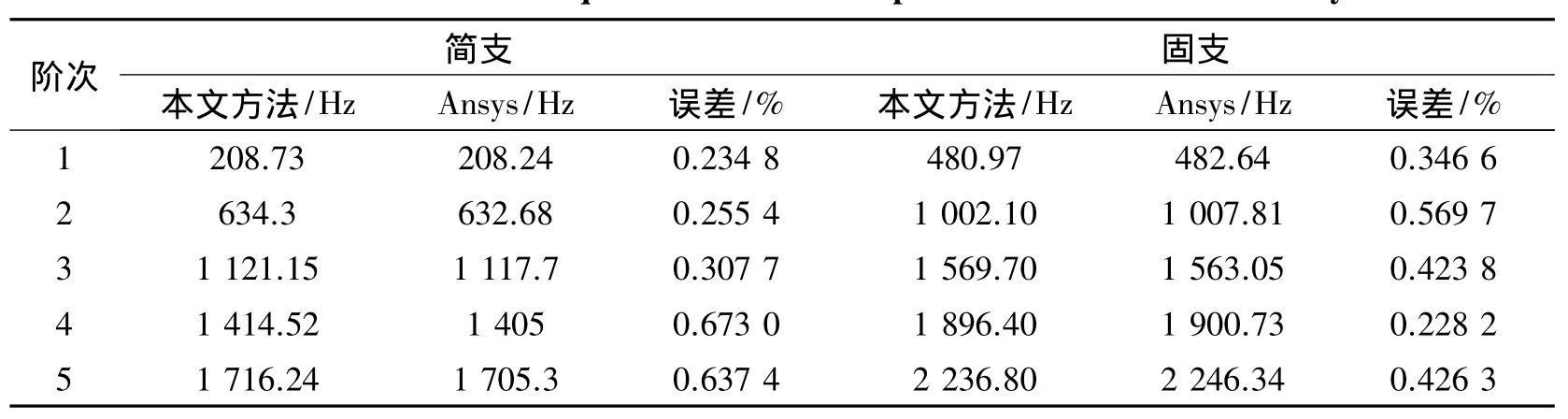
表3 不同边界条件下圆板的前5阶固有频率Table 3 The first five natural frequencies for circular plates with different boundary conditions

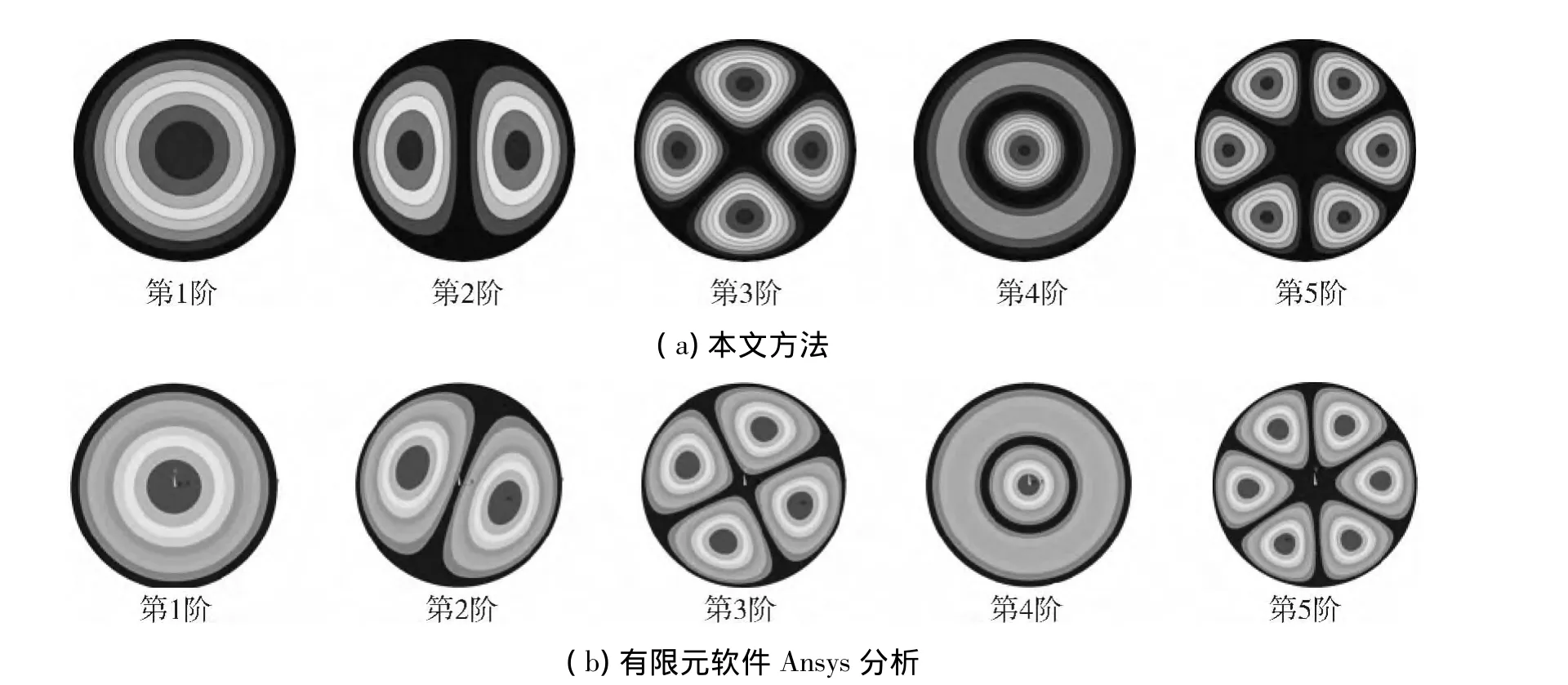
图3 简支边界圆板前5阶振型Fig.3 The first five mode shapes for simply supported circular plates

为了验证本文方法获得圆柱型正交各向异性材料圆板自由振动振型的正确性，图3给出了周边简支边界条件下，本文方法和有限元软件Ansys仿真分析的圆柱型正交各向异性圆板自由振动的前5阶振型图。通过图3可以清楚得看到两者获得的模态振型也是相一致的。

3 结束语

本文基于改进的Fourier-Bessel级数方法研究了圆柱型正交各向异性圆板在复杂边界条件下的自由振动分析。通过将圆柱型正交各向异性圆板自由振动的位移函数表示为标准的Fourier-Bessel级数和辅助多项式级数的形式，有效地提高了位移函数在边界条件的连续性。基于能量原理，利用Rayleigh-Ritz方法将变系数四阶偏微分方程的求解问题转化为矩阵特征值问题。通过矩阵特征值和特征向量的分析，获得了圆柱型正交各向异性圆板自由振动的固有频率和对应的模态振型。

同时本方法在圆板结构振动建模时，对于边界条件的处理上，采用了均匀分布的横向位移弹簧和扭转约束弹簧来模拟，通过改变不同的弹簧刚度系数实现了不同边界条件的模拟。因此本方法实现了不同边界条件下圆柱型正交各向异性圆板振动的统一数学模型。最后，通过数值算例的仿真分析，并与文献、有限元结果进行对比，证明了方法的正确性。

本文的方法也可以扩展到圆柱型正交各向异性圆环板的振动分析，并且本文对于圆柱型正交各向异性圆板结构的参数设计及结构动力学优化具有指导意义。

［1］ZHOU Z H，WONG K W，XU X S，et al.Natural vibration of circular and annular thin plates by Hamiltonian approach［J］.Journal of Sound and Vibration，2011，330(5):1005-1017.

［2］VISWANATHAN K K，SYAZWAN M S F，MOHAMAD M N，et al.Free vibration of symmetric angle-ply laminated annular circular plates［J］.International Journal of Engineering and Technology，2013，5(4):3554-3569.

［3］LIN C C，TSENG C S.Free vibration of polar orthotropic laminated circular and annular plates［J］.Journal of Sound and Vibration，1998，209(5):797-810.

［4］HUA Hongxing，SOL H，de WILDE W P.Identification of plate rigidities of a circular plate with cylindrical orthotropy using vibration data［J］.Computers and Structures，2000，77(1):83-99.

［5］KANG J H.Three-dimensional vibration analysis of thick，circular and annular plates with nonlinear thickness variation［J］.Computers and Structures，2003，81(16):1663-1675.

［6］GUPTA U S，ANSARI A H.Free vibration of polar orthotropic circular plates of variable thickness with elastically restrained edge［J］.Journal of Sound and Vibration，1998，213(3):429-445.

［7］GUPTA U S，ANSARI A H，SHARMA S.Buckling and vibration of polar orthotropic circular plate resting on Winkler foundation［J］.Journal of Sound and Vibration，2006，297(3/4/5):457-476.

［8］GUPTA A P，BHARDWAJ N.Free vibration of polar orthotropic circular plates of quadratically varying thickness resting on elastic foundation［J］.Applied Mathematical Modelling，2005，29(2):137-157.

［9］BHARDWAJ N，GUPTA A P，CHOONG K K.Asymmetric vibration of polar orthotropic annular circular plates of quadratically varying thickness with same boundary conditions［J］.Shock and Vibration，2008，15(6):599-617.

［10］KANG Wook，LEE N H，PANG Shusheng，et al.Approximate closed form solutions for free vibration of polar orthotropic circular plates［J］.Applied Acoustics，2005，66(10):1162-1179.

［11］LI W L，ZHANG Xuefeng，DU Jingtao，et al.An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports［J］.Journal of Sound and Vibration，2009，321(1-2):254-269.

［12］LI W L.Vibration analysis of rectangular plates with general elastic boundary supports［J］.Journal of Sound and Vibration，2004，273(3):619-635.

［13］DU Jingtao，LI Wen L，JIN Guoyong，et al.An analytical method for the in-plane vibration analysis of rectangular plates with elastically restrained edges［J］.Journal of Sound and Vibration，2007，306:908-927.

［14］DU Jingtao，LI Wen L，LIU Zhigang.Free vibration of two elastically coupled rectangular plates with uniform elastic boundary restraints［J］.Journal of Sound and Vibration，2009，330(4):788-804.

［15］罗祖道，李思简.各向异性材料力学［M］.上海:上海交通大学出版社，1994:201-206.

LUO Zudao，LI sijian.Mechanics of anisotropic materials［M］.Shanghai:Shanghai Jiao Tong University Press，1994:201-206.