网状可展开天线经编金属丝网的力学性能分析
2018-04-10朱日升张逸群杨东武杨癸庚
朱日升, 张逸群, 杨东武, 杨癸庚
(西安电子科技大学 电子装备结构设计教育部重点实验室,陕西 西安 710071)
鉴于火箭运载空间和能力限制,可展开性成为现代大口径星载天线的典型特征之一.网状可展开天线具有形面精度高、收纳率高、面密度小等特点,是目前大口径高精度可展开天线的研究热点.根据柔性金属丝网的支撑形式和桁架展开驱动方式的不同,网状可展开天线可分为缠绕肋、径向肋、周边桁架和构架式等几种类型[1-3].周边桁架可展开天线是目前大型高精度可展开天线的主流形式,该类型天线主要由上、下网面,金属丝网,环形桁架以及调节索组成,如图1所示.经编金属丝网被铺设在上网面,火箭发射时保持折叠收拢的状态; 卫星进入运行轨道后要求编织金属丝网能安全展开,且展开后网孔尺寸需要满足天线的工作频段要求,保证天线正常工作.

图1 周边桁架网状天线的基本组成结构
经编金属丝网被广泛应用于可展开天线[4],其编织结构、网孔形状、尺寸大小和网面各向延展性等因素直接影响天线的电性能与力学性能[5].在实际应用中,天线的工作频段(波长)往往决定了金属丝网的网孔大小,因此,在设计索网结构的初始形态时,应结合丝网的力学性能分析其对索网结构的影响,以保证天线的形面精度、结构的稳定性和网孔大小满足天线的工作要求.目前,虽然文献[6]已将经编金属丝网广泛应用于网状可展开天线,但尚未有公开文献涉及丝网的力学特性分析.而国内,文献[7-8]主要是通过丝网的拉伸实验研究其力学性能,但缺少必要的理论分析基础.文献[9]以双梳锻类结构丝网为研究对象,建立其有限元模型,并实现了静力学分析,但是缺少对模型准确性较为全面的验证.
针对上述问题,笔者以网眼式金属丝网为研究对象,建立其三维几何模型,基于丝网拉伸过程一直处于黏结接触状态的假设,采用增广的拉格朗日法推导了丝网考虑接触问题后的增量有限元求解方程,实现了丝网的力学性能分析; 最后结合丝网双向拉伸的仿真分析和实验,通过对比仿真与实验数据,验证了丝网力学性能分析方法的正确性,丝网的仿真分析结果可真实反映出实物的力学特性.
1 经编金属丝网的三维几何建模

图2 网眼式经编金属丝网
由编织工艺学可知,经编金属丝网是由多个最小重复结构单元组成的周期性结构,最小重复结构之间通过线圈在纵向的相互穿套实现连接,其结构复杂多变.根据经编线圈的结构特点,可以将线圈主干与延展线视为一个整体,如图2所示.纺织学者对经编结构几何描述的研究已有60余年,但关于其三维几何建模的研究还处于起步阶段.目前,学者一般基于文献[10-11]提出的三维线圈模型,根据特定的编织结构,定义描述线圈形状的型值点三维坐标,然后采用非均匀有理B样条(Non-Uniform Rational B-Splines,NURBS)曲线拟合得到线圈的中心线走向,最终线圈间通过连接对应的延展线型值点,可建立得到丝网的三维几何模型[12-13].
丝网在编织过程中,其单丝在经编线圈中的走向弯曲多变,为能较好地描述线圈的实际形状,文中共采用11个型值点定义成圈线圈的形状,若忽略线圈的倾斜,线圈的几何形状如图3(a)所示.其中,线圈主干主要由型值点P0~P6点所定义的曲线构成; 成圈线圈的延展线主要由P6~P10点所定义的曲线构成,起着连接上下横列线圈的作用.丝网线圈的型值点P0~P10三维坐标由线圈的理论形状确定,而针对丝网实际编织过程中线圈存在的误差和不一致性,型值点也可通过实测获得.最终由NURBS曲线拟合得到最小重复结构如图3(b)所示,丝网局部的几何模型如图3(c)所示.
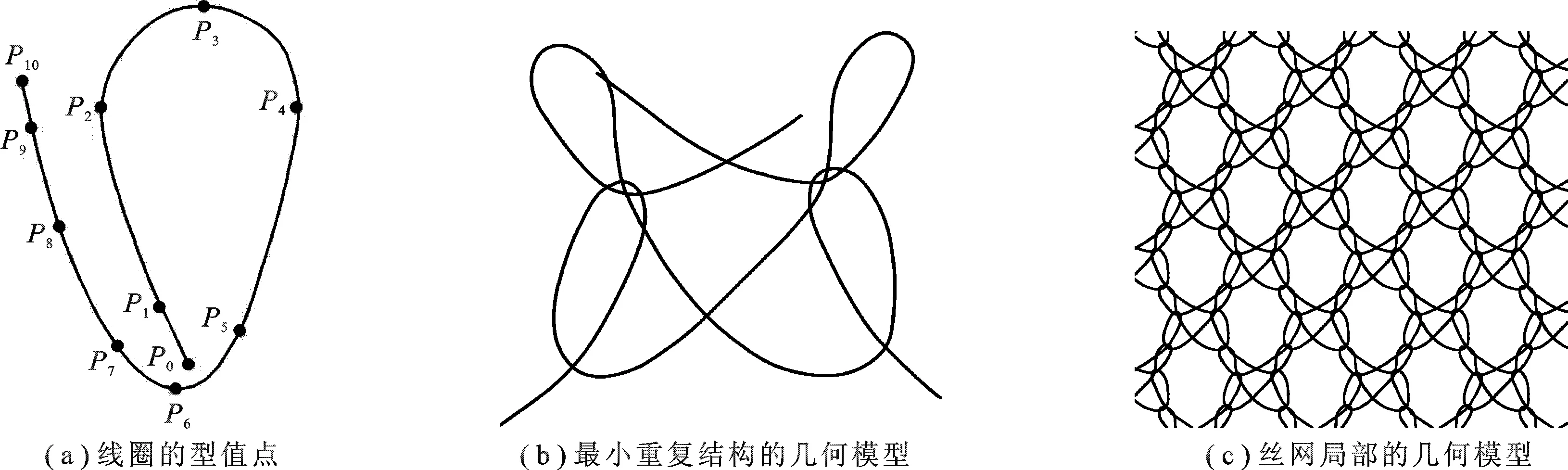
图3 网眼式经编金属丝网的几何模型
2 经编金属丝网的有限元分析
2.1 弹性体有限元方程
一般情况下,弹性体基于初始构型的当前平衡关系,其虚功方程为
(1)
其中,Pv和Ps分别为作用在弹性体上的体积力和面力,q、σ和ε分别表示弹性体的位移、应力和应变.式(1)的左端为由变形引起的内力虚功,右端项分别为体积力及面力做的虚功.进而,根据虚功原理,可得到弹性体的有限元方程为
(KL+KNL)q=R-RS,
(2)
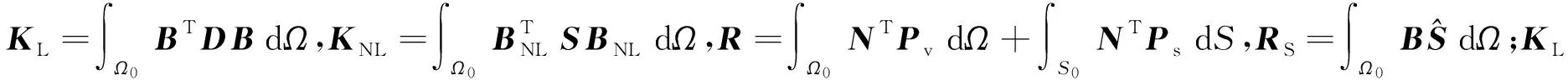
2.2 丝网单丝间的交叉接触分析
丝网内相互串套的线圈单丝以及相互交叉的延展线单丝存在着高度非线性的交叉接触问题,直接影响丝网的力学性能,因此,如何有效地简化并实现丝网的接触分析具有重要意义.通过观察丝网的双向拉伸过程可知,单丝间的滑动位移量相比于线圈的变形量是微小的,进而,为简化丝网的接触问题且保证其迭代求解的收敛性,假设拉伸过程中丝网发生接触的单丝一直处于黏结接触状态,忽略丝网在编织过程中线圈形状的不一致性,假设丝网的每个最小重复结构对应的网孔形状和大小均相同.下面以丝网任意一处单丝的交叉接触为例,如图4所示,描述含接触问题的弹性体有限元求解过程.
2.2.1黏结接触状态的约束条件
任意t时刻的黏结接触状态约束条件[14]可归结为
(7)
其中,t-ΔtξA和t-ΔtξB分别是接触体A和目标体B在(t-Δt)时刻接触点的节点坐标;tnB为目标体B上接触点的单位法向量.

图4 丝网单丝之间接触的描述
式(4)和式(6)表示黏结接触的切向摩擦力条件,且接触体间处于静摩擦状态,μτ为静摩擦系数;tqT为接触体A、目标体B上对应接触点对切向的相对滑动位移.
式(5)表示接触面上的法向接触力为压力,接触力的符号由图4沿坐标系z的正向定义.
2.2.2黏结接触状态下的接触力描述
含接触问题的弹性体在满足接触约束方程的前提下,其虚功方程可表示为
(8)
其中,右端的第3项为接触力做的虚功,即
(9)
构造势能泛函时,以增广的拉格朗日乘子法将接触约束条件引入势能泛函中,可定义其广义泛函为
Π=Πu+ΠCL+ΠCP,
(10)
其中,Πu为不包括接触约束条件的势能;ΠCL和ΠCP分别为以拉格朗日乘子法和罚函数法引入接触约束条件的附加泛函.基于黏结接触问题的约束条件,所构造的ΠCL和ΠCP可表示为
其中,N、τ1和τ2分别是图4接触面局部坐标系的法向、切向1和切向2.令δΠ=δΠu+δΠCL+δΠCP=0,则有
(13)
结合式(13)与式(8)可知,黏结接触状态下接触力与拉格朗日乘子λ、罚数α间的关系为
Fc=-λ-αP(qA-qB)-αNgc,
(14)
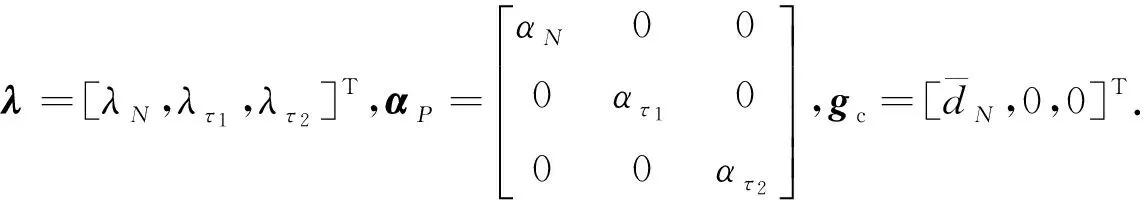
2.3 弹性体黏结接触的有限元方程
基于虚功原理,对于考虑接触问题的弹性体,其增量形式的有限元求解方程[14]为
(KL+KNL) Δq=R+Qc-RS,
(15)
其中,Δq为节点位移增量,Δq=t+Δtq-tq,tq和t+Δtq分别为t和t+Δt时刻的节点位移向量;Qc为等效节点接触力.等效节点接触力Qc可由接触力Fc表示为
(16)
其中,T为坐标转换矩阵.假设αN=ατ1=ατ2=α,则第k对接触点对的等效节点接触力(Qc)k可简化为
(17)
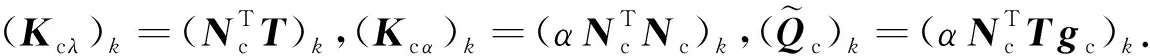
黏结接触状态的约束条件式(3)和式(4)可写成
(18)
将式(17)代入式(15),并结合约束条件式(18),基于增广拉格朗日乘子法的黏结接触状态增量形式有限元平衡方程为
(19)

式(19)属于静态接触问题,以Newmark隐式算法迭代求解,则求解的隐式算法递推公式为
(20)
3 经编金属丝网力学性能的仿真与实验对比

图5 双向拉伸的金属丝网变形示意图
为说明文中方法的正确性,对1 m×1 m方形丝网结构分别进行了双向拉伸的仿真分析和实验.由于丝网四周均受相同的载荷拉伸时,其横、纵向产生的承载力通过成圈线圈结构相互影响制约,单丝的残余预应力相比于其所受的承载力是微小的,因而仿真与实验中尚未考虑丝网的应力释放问题.
记丝网的横向平行于X轴,纵向平行于Y轴,如图5所示,丝网四周受相同载荷拉伸后,横向、纵向应变可定义为
(21)
其中,X0和Y0分别为丝网横向和纵向的初始长度,X和Y分别为丝网受双向拉伸后的横向和纵向长度.
网眼式经编金属丝网的具体参数如下: 纵密32个/(5 cm),横密25个/(5 cm),丝网单丝的材料为不锈钢丝,直径为 0.05 mm,弹性模量为 1 200 MPa,泊松比为0.3.对丝网进行双向拉伸仿真分析,仿真的横、纵向应变结果列于表1中.
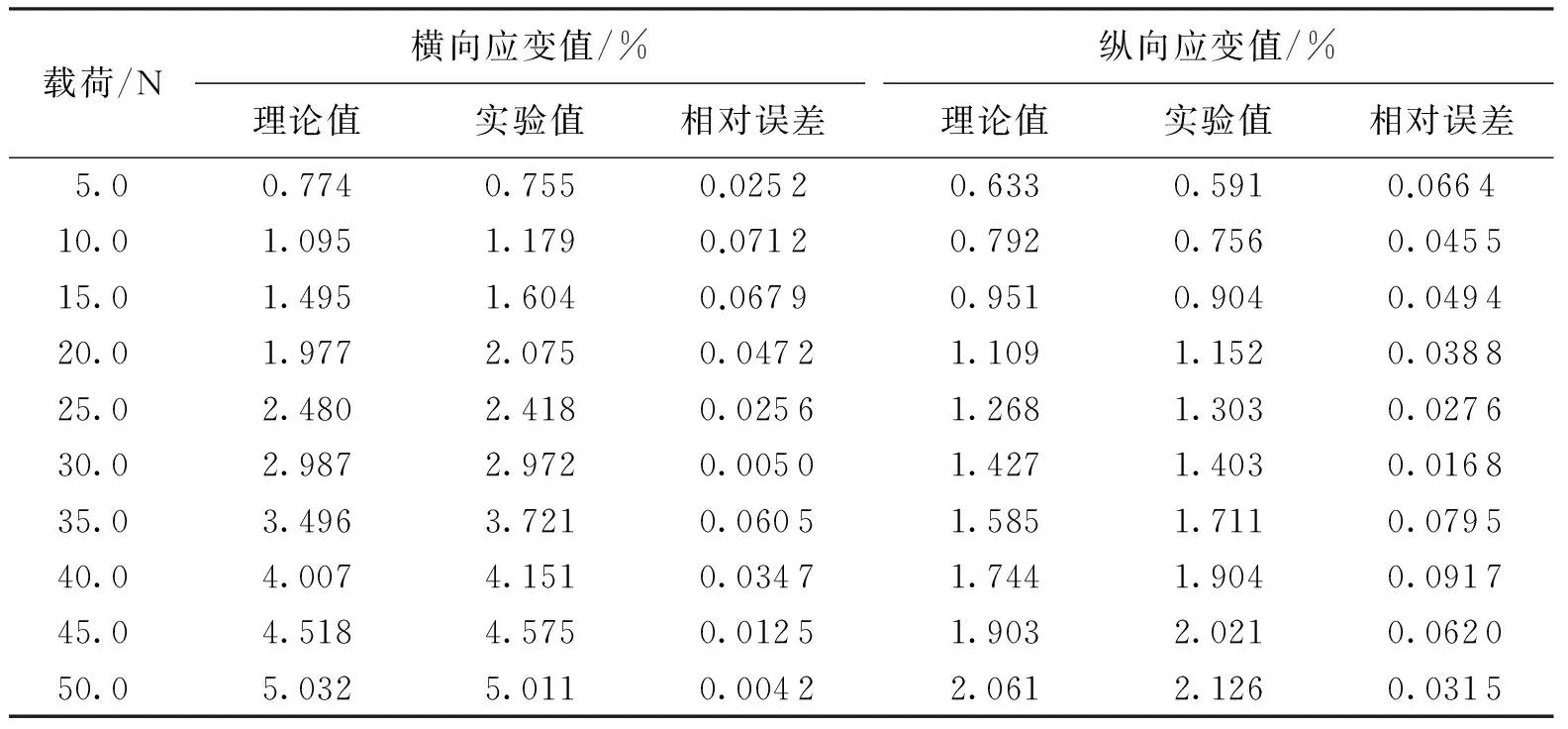
表1 丝网双向拉伸的横纵向应变值

图6 丝网的双向拉伸实验
丝网的双向拉伸实验由如图6(b)所示的四周均载受力-变形试验台实现,实验步骤如下:取 1 m× 1 m 规格的金属丝网作为实验对象,为避免丝网在拉伸过程中发生滑移,对试样夹头处进行特种胶处理.丝网四周的载荷由初始的 5 N/m 加载至 50 N/m,即每次加载均在每边平稳放置5N的砝码,载荷的加载次数计为10次.每次加完砝码待稳定后,测量横向和纵向的丝网伸长量,计算其应变值.丝网双向拉伸的横、纵向应变值列于表1中,图7为双向拉伸的丝网其仿真与实验的拉伸曲线图.

图7 双向拉伸的丝网其仿真与实验的拉伸曲线图
从表1可知,仿真与实验的横向应变值最大误差为0.071 2,平均误差为0.035 4; 纵向应变值的最大误差为 0.091 7,平均误差为 0.050 9,说明了文中丝网力学分析方法的正确性,其较真实地反映出实际结构的力学性能.而从图7可知,仿真与实验的横、纵向拉伸曲线趋势基本一致,拉伸初期曲线呈现出微弱的非线性; 随着载荷的增加,曲线段逐渐呈线性.当丝网的横、纵方向承受相同的载荷时,其横向伸长量要大于纵向伸长量,呈现出较强的各向异性特点.这是因为参与编织的金属单丝沿结构的纵向穿套成圈,横向由延展线连接,当丝网受双向拉伸时,纵向拉伸力主要由圈柱承载,横向拉伸力主要由圈弧承载,圈柱受到外力后易伸直,变形量远远小于横向圈弧的转移和伸直的变形量.因此,丝网承载相同的载荷时,其横向伸长量均大于纵向伸长量.
洙赵新河流域西靠黄河,东临南阳湖,北接梁济河流域,南与万福河和东鱼河搭界,属黄泛冲积平原,地势西高东低,流域总面积4 206 km2。其中菏泽市境内流域面积4 119 km2,流域内耕地 431万亩(28.73万 hm2)、人口450万人,粮食单产600 kg以上,棉花单产60 kg以上。含有京九铁路、兖新铁路、菏泽电厂、济菏高速、巨野煤矿等重要保护目标。
4 结 束 语
为了实现含接触问题的经编金属丝网力学分析,文中建立了丝网的三维几何模型,并基于增广拉格朗日法,将接触约束方程引入结构的势能泛函中,推导了丝网力学分析的增量有限元求解方程.通过对比丝网双向拉伸的仿真和实验数据,说明了分析方法的有效性.分析结果表明,网眼式金属丝网呈现出较强的各向异性特性,可为未来索网-金属丝网整体结构找形分析与设计、金属丝网的铺设过程提供参考.
文中求解接触问题时,一些接触参数选取主要是基于大量仿真与实验对比的总结获得.针对经编金属丝网,如何给出通用化的参数选取准则,将是下一步研究的方向之一.
参考文献:
[1] MIURA K, MIYAZAKI Y. Concept of the Tension Truss Antenna[J]. AIAA Journal, 1990, 28(6): 1098-1104.
[2]MEGURO A, SHINTATE K, USUI M, et al. In-orbit Deployment Characteristics of Large Deployable Antenna Reflector Onboard Engineering Test Satellite Ⅷ[J]. Acta Astronautica, 2009, 65(9/10): 1306-1316.
[3]DUAN B Y, YOU G Q. Optimization of Large Cable-mesh Surface Antenna with Both Deployed and Retracted States in Space[C]//Proceedings of the 2006 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Reston: AIAA, 2006: 943-950.
[4]MIURA A, TANAKA M. A Mesh Reflecting Surface with Electrical Characteristics Independent on Direction of Electric Field of Incident Wave[C]//Proceedings of the 2004 IEEE Antennas and Propagation Society Symposium. Piscataway: IEEE, 2004: 33-36.
[5]赛兴鹏, 秦庆彦. 可收展卫星天线用金属网技术研究进展[J]. 贵金属, 2011, 32(1): 82-87.
SAI Xingpeng, QIN Qingyan. Advances on the Metal Gauzes in Drawing-in and Opening-up Satellite Antenna[J]. Precious Metals, 2011, 32(1): 82-87.
[6]BASSILY S F, URIBE J. Mesh Tensioning, Retention and Management Systems for Large Deployable Reflectors: US Patent 6384800B1[P]. 2002.
[7]李楠, 蒋金华, 邵光伟, 等. 经编网格织物的性能研究[J]. 针织工业, 2016(1): 23-27.
LI Nan, JIANG Jinhua, SHAO Guangwei, et al. Performance Study of Warp Knitted Eyelet Fabric[J]. Knitting Industries, 2016(1): 23-27.
[8]李欢, 王少鹏, 黄春良, 等. 经编金属丝网状织物拉伸性能研究[J]. 针织工业, 2016(11): 22-25.
LI Huan, WANG Shaopeng, HUANG Chunliang, et al. Study of Tensile Properties of Warp Knitted Metal Mesh Fabric[J]. Knitting Industries, 2016(11): 22-25.
[9]LI T J, JIANG J, SHEN T T, et al. Analysis of Mechanical Properties of Wire Mesh for Mesh Reflectors by Fractal Mechanics[J]. International Journal of Mechanical Sciences, 2015, 92: 90-97.
[10]GOKTEPE O. Use of Non-uniform Rational B-splines for Three-dimensional Computer Simulation of Warp Knitted Structures[J]. Turk Journal Engineer Environ Science, 2001, 25(4): 369-378.
[11]GOKTEPE O, HARLOCK S C. A 3D Loop Model for Visual Simulation of Warp-knitted Structures[J]. Journal of the Textile Institute, 2002, 93(1): 11-28.
[12]XU H Y, CHEN N L, JIANG J H, et al. 3D Simulation of Warp Knitted Structures with a New Algorithm Based on NURBS[J]. Fibres and Textiles in Eastern Europe, 2015, 23(1): 57-60.
[13]JIANG G M, GU L Y, CONG H L, et al. Geometric Model for Multi-axial Warp-knitted Fabric Based on NURBS[J]. Fibres and Textiles in Eastern Europe, 2014, 105(3): 91-97.
[14]曾攀. 塑性非线性分析原理[M]. 北京: 机械工业出版社, 2015: 210-225.
