机械故障诊断的稀疏特征提取方法

贺王鹏， 孙　伟， 苏　博， 闫允一， 郭宝龙

(西安电子科技大学 空间科学与技术学院，陕西 西安 710071)

重大机械设备不仅是重要的工业制造产品，也是关键的生产资料，其使用几乎覆盖了后续更新产品的设计、制造、测试和服役保障等诸多环节．然而，这些关键设备在高温腐蚀、复杂极端、重载强度和长时间疲劳等恶劣的工作条件下运行，零部件不可避免会发生性能退化和故障失效[1]．

旋转机械关键零部件存在局部损伤故障时，其运行过程中会产生周期性冲击响应特征，且每个有用冲击特征信息并不是孤立的数据点，而是具有簇稀疏的点集合．在机械设备运行过程中，采集得到的振动信号不可避免地会受到系统噪声和环境噪声的干扰．当设备存在早期微弱故障时，故障的特征本身比较微弱，有用的故障特征信息往往被淹没在强大的背景噪声中[2]．机械故障动态信号的微弱性主要表现在两个方面:故障损伤信号特征本身非常微弱，如早期故障;有用故障特征信号被机械系统多干扰源和强噪声所淹没，导致难以识别，这使得关键设备的状态监测和故障诊断的难度不断增大[3]．因此，研究先进的故障特征提取技术，具有重要的工程意义和实用价值．

近年来工程中广泛应用的傅里叶变换和小波变换等非平稳信号处理方法，其本质都是基于内积变换原理的特征波形基函数分解．其中，基于小波的稀疏特征提取技术得到了国内外学者的广泛关注[4]．然而，对于复杂多变信号，小波变换在信号稀疏特征提取方面缺乏自适应性．针对此类信号，建立在多种基函数之上的原子分解方法(如匹配追踪和基追踪)可以取得较好的效果[5]．目前广泛应用的稀疏优化模型中，基于l1范数的凸正则化得到各个领域的青睐．然而，非凸正则化往往能够取得更好的处理效果，但是非凸正则项的引入可能会牺牲目标函数的凸性[6]．针对此问题，文献[7]提出了一种巧妙的解决思路:通过适当的约束非凸正则项(惩罚函数)，使其与凸的二次数据保真项进行平衡，可以保证目标函数整体仍然为凸．基于上述思想，一些学者在近年来构造出具体的优化模型，并取得了比凸正则化更佳的应用效果[8]．

笔者针对旋转机械的周期簇稀疏故障特征提取问题，深入研究了一种周期重叠簇稀疏(Periodic Overlapping Group Sparsity， POGS)信号优化特征提取算法[6]．旨在从含噪观测数据中提取周期簇稀疏故障特征，所研究的POGS算法构造了有效的优化目标函数，该目标函数中的正则项(惩罚函数)选用非凸惩罚函数来增强周期性特征的稀疏性，并且证明了非凸可控化参数在一定约束条件下可以保证目标函数整体为凸．引入优控极小化方法(Majorization-Minimization， MM)[9]，推导出高效的迭代收敛算法用于POGS算法优化问题的求解．将所提出的POGS算法应用于仿真信号，定量地分析了其有效性．最后将POGS算法应用于轴承故障特征提取中，进一步验证了其在稀疏故障特征提取中的优越性．

1　问题描述和非凸惩罚函数

1.1　问题描述

文中研究时域周期性簇稀疏故障特征的优化提取问题．假设观测到的含噪信号y可表示为

y=x+w,

(1)

其中，x表示具有周期簇稀疏特征的信号成分；w表示背景噪声，通常假设为高斯白噪声．需要说明的是，在通用的故障诊断降噪模型中，一般假设观测信号由有用振动成分和干扰噪声组成，而文中直接将观测信号构造为稀疏故障特征和噪声的合成信号，旨在提取出与故障直接相关的周期性稀疏特征．

1.2　非凸惩罚函数

文中选用非凸惩罚函数来增强周期性特征的稀疏性，假设非凸惩罚函数φ:R→R，满足如下特性:

(1)φ在实数范围内连续．

(2)φ在R{0}范围内二阶可微．

(3)φ在R+范围内递增且是凹的．

(4)φ是对称函数，即φ(-x)=φ(x)．

图1 绝对值凸函数与典型的非凸惩罚函数图(a=2)

(5)φ′(0+)=1(在0处的斜率为1)．

(6) ∀x≠0，存在φ″(x)≥φ″(0+)．

文中使用的非凸惩罚函数由一个标量参数灵活地实现非凸程度的调节，该标量参数标记为a>0．定义符号φ(x;a)来表示非凸惩罚函数的参数化形式．满足以上假设的典型非凸惩罚函数有对数函数型(log)、有理分式函数型(rat)及反正切函数型(arctan)，如表1所示．这几类典型的参数化非凸惩罚函数φ还具有如下特性:φ″(0+;a)= -a和φ(x;0)= |x|．绝对值凸函数和满足本节假设的典型非凸惩罚函数如图1所示．由图1中可以观察得到，反正切型(arctan)惩罚函数比其他两种惩罚函数的非凸性更强，可以更大限度的增强提取特征的稀疏性．

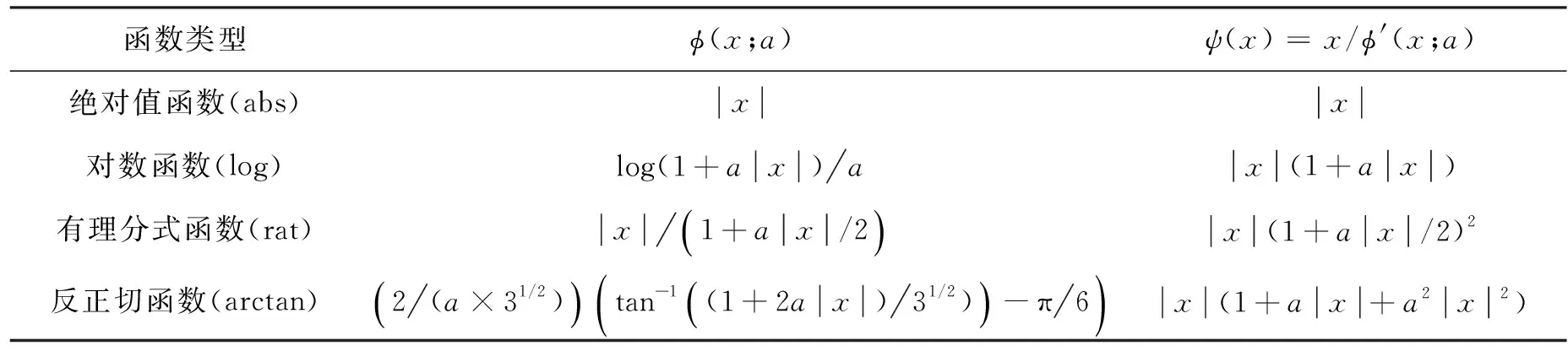
表1　绝对值凸函数与典型的非凸稀疏惩罚函数

2　周期重叠簇稀疏信号优化特征提取算法

针对旋转机械的核心零部件在发生故障时常伴随周期性非平稳冲击特征的先验知识，研究一种高效的周期重叠簇稀疏(POGS)信号优化特征提取算法．POGS算法具体包括优化问题的构造、凸函数约束条件和快速收敛算法推导．

2.1　POGS算法优化问题的构造

POGS算法构造如下的无约束优化问题:

(2)

其中，P为优化问题的目标函数；y∈RN，为观测得到的含噪信号；b为二进制的序列b= {b0，b1，…，bK-1}，bk∈ {0，1}；惩罚函数φ:R→R，满足1.2节中定义的假设条件．POGS算法优化问题在惩罚函数作用的对象中创造性地引入二进制权重序列b，实现了稀疏特征结构的灵活性刻画[6]．具体地，θ(x，b，n)是一个具有二进权重数据块的欧几里得范数(l2范数)，该数据块包含K个相邻的信号点, 可表示为

(3)

2.2　凸函数约束条件

通过调节非凸惩罚函数的非凸程度，可以保证POGS算法优化问题目标函数整体仍然为凸函数．其理论依据为:数据保真度项为凸的二次项(目标函数P中的第1项)，因此适当地约束非凸惩罚函数φ的非凸程度，可以保证目标函数P整体为凸函数．目标函数P为凸函数可以保证用迭代收敛算法求解时，所得到的结果不会受陷于局部最优解．

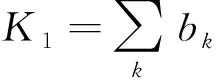
0≤a<1/(K1λ)

(4)

时，则目标函数P是严格凸的[6]．

2.3　POGS算法快速收敛求解算法

为求解POGS算法构造的优化问题，引入优控极小化方法(MM)求解所构造的目标函数，并提出了高效的迭代收敛数值算法[6]．由于可以约束所构造的优化问题为凸，所提出的迭代优化算法最终收敛于凸优化问题的全局最优解，这样可以避免非凸优化问题受困于局部最优解的难题．其中，POGS算法的正则化参数的取值，可根据噪声标准差大小进行设置[6]．为了最大化地增强提取特征的稀疏性，非凸可控化参数a在满足约束式(4)的条件下取最大值进行设置．

POGS求解算法归纳如下:

输入:y∈RN，λ，b∈{0，1}K，ε．

初始化:x=y，S={n:yn≠0}．

对n∈S，执行循环:

(2)xn=yn/(1+λrn)．

(3)S={n: |xn|>ε}．

直至收敛．

输出:x．

3　仿真信号分析

为了验证文中研究的POGS算法在周期性稀疏故障特征提取中的有效性，模拟了一组周期性冲击信号特征，并添加高斯白噪声n(t)用于模拟背景干扰噪声．仿真信号表达式为

y(t)=exp(-50t) sin(2π×50t)+n(t)．

(5)

仿真的周期性冲击信号及含噪信号波形分别如图2(a)和图2 (b)所示，其中采样频率fs= 1 000 Hz，信号长度为 2 048 个点，噪声的标准差σ= 0.33．可以观察到，在原始信号中模拟的周期性瞬态冲击分量被强大的背景噪声所淹没．为定量地分析POGS算法在提取周期稀疏特征方面的有效性，选用均方根误差(Root-Mean-Square Error，RMSE)和信噪比(Signal-to-Noise Ratio，SNR)作为评价指标．对于图2(b)中的仿真含噪信号，其均方根误差为0.328，信噪比为 -6.540 dB．

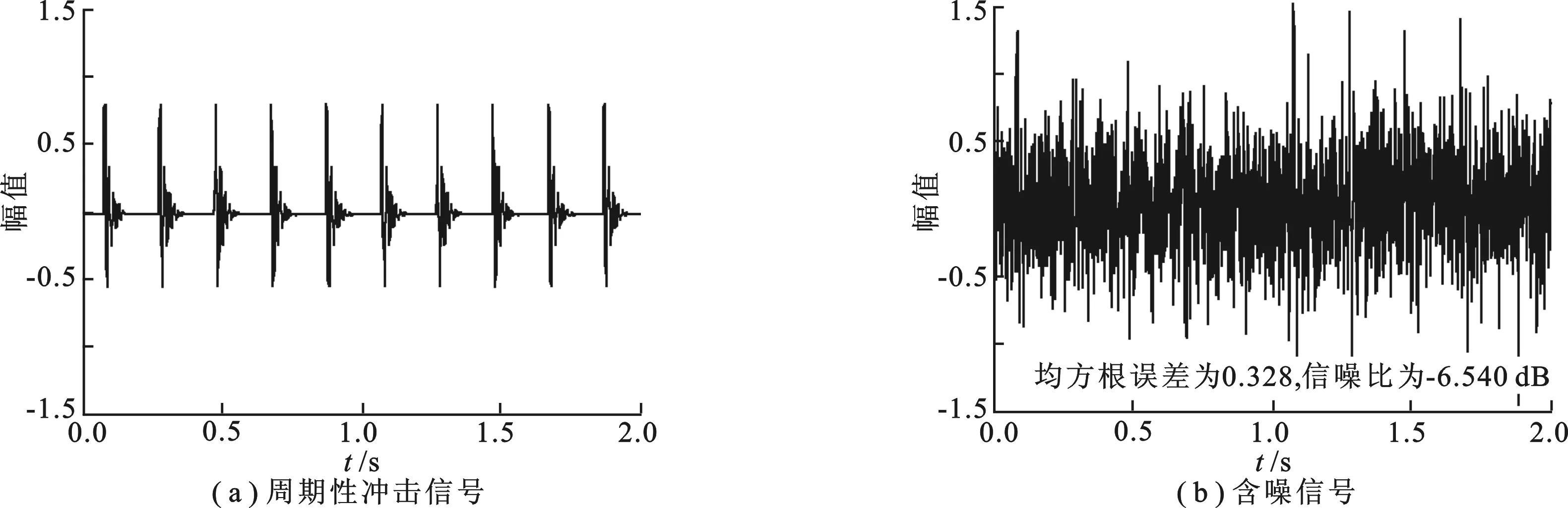
图2　仿真信号波形图

采用文中研究的POGS算法对该模拟含噪信号进行分析，其中正则化参数设置为λ= 0.152，算法迭代次数为30．POGS算法稀疏特征提取结果及优化目标函数收敛特性分别如图3(a)和图3(b)所示．在提取得到的稀疏特征波形图3(a)中，可以清晰地发现周期性冲击单元，其均方根误差为0.101，信噪比为 3.653 dB．分析结果证明了所研究的POGS算法可以准确地恢复具有周期性稀疏特征的有用信号成分，最大限度地消除了背景噪声的干扰．本例中所研究的POGS算法处理该仿真信号时运行时间仅为 0.009 s，完全满足工程中对算法实时性的要求．测试软硬件为: 联想Y40笔记本，16 GB 内存，Intel i7-5500U处理器，Matlab 2011．

图3　POGS算法稀疏特征提取结果及优化目标函数收敛图

4　实际信号验证

为验证所研究的POGS算法在机械故障特征提取中的有效性，这里将其应用于轴承故障振动信号分析中．振动信号来源于机械故障预防协会(Machinery Failure Prevention Technology Society， MFPTS)的故障模拟实验台，数据来源网址为http://www.mfpt.org/FaultData/FaultData.htm．表2中列出了测试滚动轴承的具体参数．输入轴的转频(驱动频率)为 25 Hz．由表2可以计算得到轴承内圈故障特征频率为 118.9 Hz[10]．

表2　测试滚动轴承具体参数

图4所示为采集的轴承内圈故障振动信号时域波形图，该信号的采样频率和采样长度分别为 48.828 kHz 与 9 765 点．采用文中研究的POGS稀疏优化算法对该含噪振动信号进行分析，正则化参数λ与噪声标准差大小σ成比例．本节中，针对实际测量得到的信号，背景噪声的标准差σ可表示为

σ=median(|y|)/0.674 5,

(6)

其中，median(·)为取中值函数．式(6)为文献[6]提出，并且已经在小波降噪等研究中得到了广泛的应用．利用式(6)估计得到的背景噪声标准差大小σ= 0.729，设置正则化参数λ= 0.273 4．POGS稀疏特征提取结果如图5所示，在提取得到的特征波形图中，可以清晰地发现周期性冲击单元．冲击单元间隔对应的频率与内圈故障特征频率 (118.9 Hz) 相一致．

图4 内圈故障振动信号时域图图5 POGS稀疏特征提取结果图

5　结 束 语

文中研究了机械故障信号的周期重叠簇稀疏(POGS)特征提取算法．POGS算法能够有效地从时域含噪信号中提取出具有周期簇稀疏结构的故障特征．POGS算法构造了有效的优化目标函数，该目标函数中的正则项(惩罚函数)选用非凸惩罚函数来增强周期性特征的稀疏性，并且证明了非凸可控化参数在满足一定约束条件下可以保证目标函数整体为凸．为求解POGS算法所构造的目标函数，引入优控极小化方法，推导出高效的迭代收敛数值算法，该快速求解算法最终收敛于POGS算法优化问题的全局最优解．将所提出的POGS算法应用于仿真信号，通过RMSE和SNR指标定量地分析了其有效性．最后将POGS算法应用于轴承故障特征提取中，进一步验证其在稀疏故障特征提取中的优越性．

参考文献：

[1] SMITH W A, RANDALL R B. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: a Benchmark Study[J]. Mechanical Systems and Signal Processing, 2015, 64/65: 100-131.

[2]SHAO H D, JIANG H K, ZHAO H W, et al. A Novel Deep Autoencoder Feature Learning Method for Rotating Machinery Fault Diagnosis[J]. Mechanical Systems and Signal Processing, 2017, 95: 187-204.

[3]贺王鹏, 訾艳阳, 陈彬强. 冲击特征受控极小化通用稀疏表示及其在机械故障诊断中的应用[J]. 西安交通大学学报, 2016, 50(4): 94-99.

HE Wangpeng, ZI Yanyang, CHEN Binqiang. Majorizaiton Minimization Oriented Sparse Optimization Method for Feature Extraction Technique in Machinery Fault Diagnosis[J]. Journal of Xi’an Jiaotong University, 2016, 50(4): 94-99.

[4]王勇, 冯唐智, 陈楚楚, 等. 结合自适应稀疏表示和全变分约束的图像重建[J]. 西安电子科技大学学报, 2016, 43(1): 12-18.

WANG Yong, FENG Tangzhi, CHEN Chuchu, et al. Adaptive Sparse Representation and Total Variation Constraint Based Image Reconstruction[J]. Journal of Xidian University, 2016, 43(1): 12-18.

[5]CUI L L, WU N, MA C Q, et al. Quantitative Fault Analysis of Roller Bearings Based on a Novel Matching Pursuit Method with a New Step-impulse Dictionary[J]. Mechanical Systems and Signal Processing, 2016, 68/69: 34-43.

[6]HE W P, DING Y, ZI Y Y, et al. Sparsity-based Algorithm for Detecting Faults in Rotating Machines[J]. Mechanical Systems and Signal Processing, 2016, 72/73: 46-64.

[7]NIKOLOVA M, NG M K, TAM C P. Fast Nonconvex Nonsmooth Minimization Methods for Image Restoration and Reconstruction[J]. IEEE Transactions on Image Processing, 2010, 19(12): 3073-3088.

[8]HE W P, DING Y, ZI Y Y, et al. Repetitive Transients Extraction Algorithm for Detecting Bearing Faults[J]. Mechanical Systems and Signal Processing, 2017, 84: 227-244.

[9]FIGUEIREDO M A T, BIOUCAS-DIAS J M, NOWAK R D. Majorization-minimization Algorithms for Wavelet-based Image Restoration[J]. IEEE Transactions on Image Processing, 2007, 16(12): 2980-2991.

[10]HE W P, ZI Y Y, CHEN B Q, et al. Automatic Fault Feature Extraction of Mechanical Anomaly on Induction Motor Bearing Using Ensemble Super-wavelet Transform[J]. Mechanical Systems and Signal Processing, 2015, 54: 457-480.