绳索-金属丝网组合结构力热匹配设计

李团结， 杨　丽， 李　洋， 马小飞

(1. 西安电子科技大学 机电工程学院，陕西 西安 710071;2. 中国空间技术研究院西安分院，陕西 西安 710000)

网状可展开天线[1]是上世纪末出现的一种新的可展开天线形式，由于其具有质量轻、结构简单、易于实现大口径与高增益等特点，在现有的空间在轨卫星中得到广泛的应用．这些网状可展开天线的反射面[2]是由柔性绳索与金属丝网缝制而成，在太空环境中，受剧烈温度变化影响，不同材料力热特性差异引起金属丝网与纤维绳索变形不协调，进而影响绳索丝网组合结构的预应力分布与形面精度，降低反射面电性能．因此，研究绳索丝网组合结构的力热匹配问题具有重要的意义[3-4]．

金属丝网网格细小，一般将其等效为薄膜进行处理，目前针对索膜结构[5-7]的研究主要集中在索膜结构的找形分析．文献[8]考虑索膜结构几何和材料非线性，利用动态松弛法对索杆和膜单元进行找形分析．文献[9]对倒伞式可展索膜结构的静力分析原理进行了理论推导，研究了倒伞式可展索膜结构在荷载作用下应力及位移的变化规律．文献[10]对膜结构力密度法找形的过程进行改进，引入膜面应力和索拉力作为初始条件，以节点不平衡力作为控制误差，使找形过程简洁高效．

目前已有很多对空间结构在温度载荷作用下热变形的研究．文献[11]采用子域摄动随机有限元法研究了空间结构在轨运行的热变形，考虑了结构参数受热扰动对结构热变形的影响．文献[12]通过有限元分析论证了空间反射面天线用薄膜在热载荷作用下的影响规律．文献[13]通过有限元法计算星载可展开天线太空辐射热变形，研究了基本结构参数对天线热变形的影响．文献[14]采用概率有限元法研究了材料热膨胀系数在空间温度影响下，空间可展开天线在轨运行时的热变形及其对天线形面精度的影响规律．

综上所述，为了满足我国航天事业对高精度网状天线的需求，提高网状天线在轨运行的热稳定性，文中尝试探索研究绳索丝网组合结构的力热匹配设计方法．首先，采用只承受张力的两节点杆模拟绳索，利用膜模拟金属丝网结构，建立绳索丝网组合结构力学模型；然后，分析绳索丝网组合结构热变形影响规律，并对索截面参数进行匹配设计；最后，以环形桁架网状可展开天线为算例，通过仿真验证了文中力热匹配设计方法的有效性．

1　力学模型

金属丝网网格细小，可用薄膜来等效．取单片三角形膜与索网进行分析，如图1所示．

图1 单片索网与膜单元图2 膜单元等效为杆单元

取每个索为一两节点空间杆，每个节点具有3个自由度．假定索两节点为理想的无摩擦铰节点，索材料为理想线弹性体，受力和变形满足虎克定律．将膜离散为三节点三角形单元，并进一步将三角形膜单元等价为以三角形3条边为单元的杆单元，这样原来的三角形单元就转化为沿3根杆自由伸缩的杆单元，如图2所示．3个杆单元的初始拉力可表示为[3]

(1)

其中，σx和σy为膜的应力，t为膜的厚度．

1.1　等应力膜

假设膜面各方向的应力均为σ，即等应力膜，σx=σy=σ，则式(1)变为

Ti=σLit/(2 tanβi),i=1，2，3．

(2)

设绳索材料的热胀系数为α，弹性模量为E，横截面积为Ac，膜材料的热胀系数为αm，弹性模量为Em，泊松比为μ．当环境温度变化ΔT时，绳索的张力增量 ΔF= ΔTαEAc，膜的应力变化 Δσ= ΔTEmαm/ (1-μ)，则膜的三边等效内力增量为

图3　索膜单元内力

(3)

工程上，绳索一般选用热胀系数为负的材料，即热缩冷涨，这与膜材料的热胀方向相反，如图3所示．

为保证索膜热变形协调，应保证索和膜在连接处(变形相同)张力相等，令

若L1=L2=L3=L，则β1=β2=β3=β，即三角形为等边三角形，则式(5)变为

(6)

其中，C是常数．

由式(5)和式(6)可知，由索膜热变形协调得到的索参数Ac与温度无关，但与索和膜的热胀系数及膜的几何参数有关．即当索参数为Ac时，在任一温变环境下，索的热变形量与膜的热变形量相同．

在索网结构中，索一般和两个三角形膜相连．为了保证索网结构在温变环境中热变形协调，索i的截面参数可设计为

(7)

1.2　正交各向异性膜

对于正交各向异形体，平面弹性结构内由应力组成的向量与应变组成的向量应满足下式：

(8)

其中，σx、σy和τxy分别为x、y方向应力以及xy平面内的切应力，D为平面结构的弹性矩阵，即

(9)

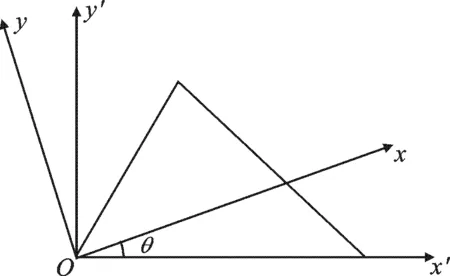
图4　平面三角形膜单元

其中，Ex、Ey、Gxy和Vxy为工程常数．

图4所示为一平面三角形膜单元，Oxy为弹性坐标系，Ox′y′为局部坐标系，两坐标系夹角为θ(逆时针为正)．

推导可以得到弹性坐标系与局部坐标系间的应力关系为

(10)

其中，c=cosθ，s=sinθ，A为变换矩阵．

对于弹性坐标系与局部坐标系下的应变，也有类似的关系[15]，即

(11)

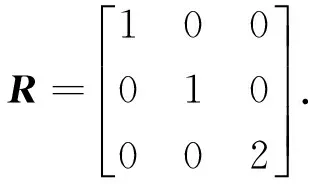
将式(10)和式(11)代入式(8)，得到

(12)

所以，局部坐标系下的正交各向异性膜的本构矩阵D′为

D′=ATDRAR-1．

(13)

在局部坐标系下，膜单元由于温度变化产生的热应力为

(14)

展开式(14)，得到

若θ=45°或135°，则

(16)

其中，Eem定义为正交各向异性膜单元的等效弹性模量．由式(1)可知，此时热应力等效到3根杆的拉力为

Ti=EemαmΔTLit/(2 tanβi),i=1，2，3．

(17)

为了保证索膜变形协调，此时索截面参数应设计为

Aci=(Eem/E) (αm/α)t(Li/(2 tanβi)),i=1，2，3．

(18)

同样，若索网三角形为等边三角形，在索网结构中，索的截面参数应设计为

Ad=(Eem/E) (αm/α)t(L/tanβ)．

(19)

为了制造方便，索可选用同一截面尺寸的绳索．因此，工程设计中，为保证绳索-金属丝网结构的热稳定性，绳索的截面尺寸应按式(7)或式(19)进行选取．若金属丝网具有正交各向异性，可采取将金属丝网弹性主轴沿与绳索局部坐标系成45°或135°的方向铺设．

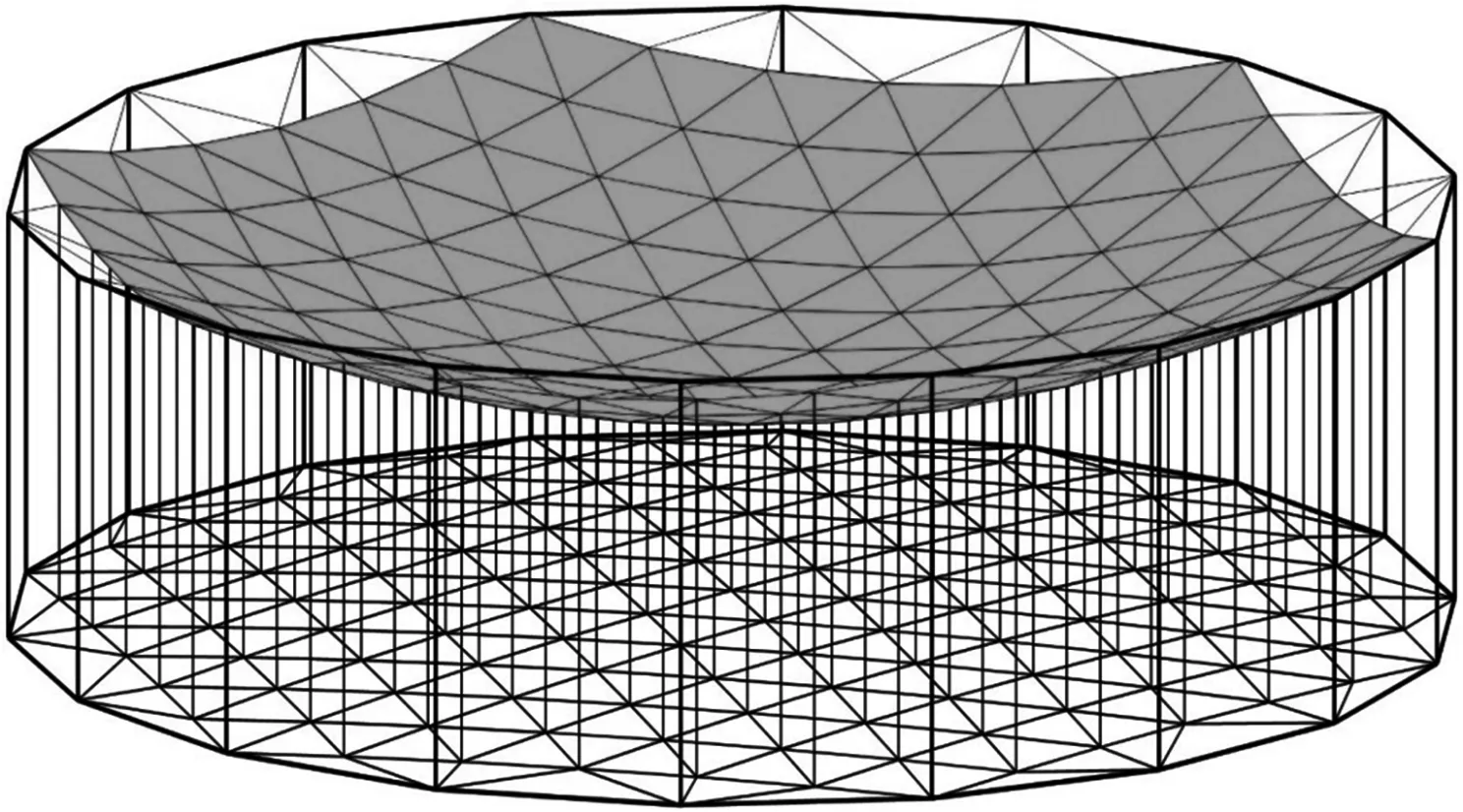
图5　环形桁架网状可展开天线

2　数值算例

如图5所示为一环形桁架网状可展开天线，由前索网、金属网面、竖向索、桁架结构以及背索网构成．天线口径为 5 m，桁架高度为 1.2 m，前网面焦距为 3 m，后网面焦距为 20 m．E= 2× 1010N/m2，α= -1× 10-6，Ac= 3.14× 10-6m2，Em= 1×1 09N/m2，αm= 1× 10-5，t= 0.1 mm，μ=0.3．

对桁架进行固定处理，设前索网索力均值为 20 N，利用平面投影法[16]对索网结构进行找形．找形后，索长度分布介于 0.417 m 到 0.446 m 之间，求得前网面索长均值L= 0.427 m，由式(7)，得到前网面索的设计横截面积Ad= 1.760× 10-5m2．天线在太空工作，最低温度低于 -100℃．在有限元软件中对天线施加低温 -100℃ 温度场进行仿真分析，前网面索取不同参数时天线热变形云图如图6所示，其中，图6(a)是前索网半径 1 mm 的热变形云图，对应的形面均方根误差为 1.284 mm; 图6(b)是力热匹配设计的索参数的热变形云图，对应的形面的均方根误差为 0.101 mm．可以看出，采用文中的力热匹配设计方法，天线在温变环境下的热稳定性得到很大的改善，形面精度的均方根误差提高了92%．

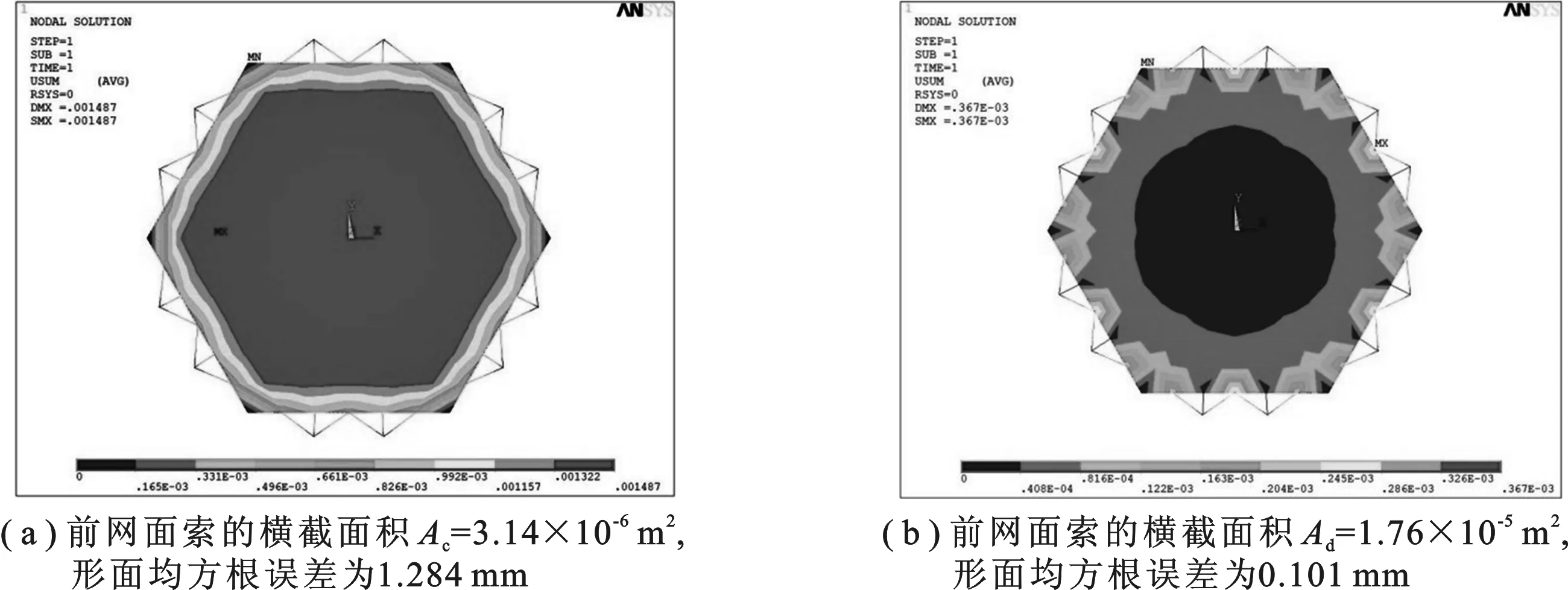
图6　天线热变形云图

3　结 束 语

文中提出了一种绳索-金属丝网组合结构力热匹配设计方法，能够保证天线在轨运行的热稳定性，得到了如下结论:

(1) 绳索-金属丝网热变形协调设计得到的绳索设计参数与温度无关，与绳索和金属丝网的热胀系数及几何参数有关．

(2) 对于正交各向异性金属丝网结构，除了绳索参数需要匹配设计，金属丝网弹性主轴应沿与绳索局部坐标系成45°或135°的方向铺设．

(3) 数值算例结果表明: 采用文中的力热匹配设计方法，天线在温变环境下的热稳定性得到很大的改善，形面精度提高了92%．

参考文献：

[1] LI T J, JIANG J, DENG H Q, et al. Form-finding Methods for Deployable Mesh Reflector Antennas[J]. Chinese Journal of Aeronautics, 2013, 26(5): 1276-1282.

[2]范叶森, 李团结, 马小飞, 等. 一种等张力空间索网结构找形方法[J]. 西安电子科技大学学报, 2015, 42(1): 49-55.

FAN Yesen, LI Tuanjie, MA Xiaofei, et al. Form-finding Method of Equal Tension Cable Networks for Space Mesh Antennas[J]. Journal of Xidian University, 2015, 42(1): 49-55.

[3]王辉, 宋燕平, 马小飞. 非对称环形天线型面稳定性的参数匹配设计方法[J]. 西安电子科技大学学报, 2017, 44(3): 122-128.

WANG Hui, SONG Yanping, MA Xiaofei. Parameter Matching Design Method to Keep Asymmetrical Astromesh Reflector Surface[J]. Journal of Xidian University, 2017, 44(3): 122-128.

[4]任榕, 解启林, 高永新, 等. 一种应用于电子封装的热匹配工艺设计[J]. 电子工艺技术, 2011, 32(3): 141-144.

REN Rong, XIE Qilin, GAO Yongxin, et al. Thermal Matching Technique Design for Electronics Packaging[J]. Electronics Process Technology, 2011, 32(3): 141-144.

[5]ANDO K, MITSUGI J, SENBOKUYA Y. Analyses of Cable-membrane Structure Combined with Deployable Truss[J]. Computers and Structures, 2000, 74(1): 21-39.

[6]DINH T D, REZAEI A, PUNURAI W, et al. A Shape Optimization Approach to Integrated Design and Nonlinear Analysis of Tensioned Fabric Membrane Structures with Boundary Cables[J]. International Journal of Solids and Structures, 2016, 83: 114-125.

[7]SAKAMOTO H, PARK K C, MIYAZAKI Y. Evaluation of Membrane Structure Designs Using Boundary Web Cables for Uniform Tensioning[J]. Acta Astronautica, 2007, 60(10/11): 846-857.

[8]BARNES M R. Form Finding and Analysis of Tension Structures by Dynamic Relaxation[J]. International Journal of Space Structures, 1999, 14(2): 89-104.

[9]殷志祥, 孙芳锦. 倒伞式可展索膜结构静力特性分析[J]. 工程力学, 2006, 23(7): 160-164.

YIN Zhixiang, SUN Fangjin. The Analysis of Static Mechanical Properties of Deployable Upside-down Umbrella Membrane Structures[J]. Engineering Mechanics, 2006, 23(7): 160-164.

[10]周树路, 叶继红. 膜结构找形方法—改进力密度法[J]. 应用力学学报, 2008, 25(3): 421-424.

ZHOU Shulu, YE Jihong. Modified Force-density Method for Form-finding of Membrane Structures[J]. Chinese Journal of Applied Mechanics, 2008, 25(3): 421-424.

[11]范立佳, 向志海, 薛明德, 等. 空间结构热变形的子域摄动随机有限元解法[J]. 清华大学学报, 2010, 50(7): 1099-1103.

FAN Lijia, XIANG Zhihai, XUE Mingde, et al. Perturbation Based Sub-domain Stochastic Finite Element Method for Analyzing Thermal Deformations of Space Structures[J]. Journal of Tsinghua University, 2010, 50(7): 1099-1103.

[12]JENKINS C H, FAISAL S M. Thermal Load Effects on Precision Membranes[J]. Journal of Spacecraft and Rockets, 2001, 38(2): 207-211.

[13]朱敏波, 曹峰云, 刘明治, 等. 星载大型可展开天线太空辐射热变形计算[J]. 西安电子科技大学学报, 2004, 31(1): 28-31.

ZHU Minbo, CAO Fengyun, LIU Mingzhi, et al. The Calculation of Thermal Radiaiton Distortion for Large Deployable Antennas in Satellites[J]. Journal of Xidian University, 2004, 31(1): 28-31.

[14]TANG Y Q, LI T J, WANG Z W. Surface Accuracy Analysis of Large Deployable Antennas[J]. Acta Astronautica, 2014, 104(1): 125-133.

[15]TING E C, SHIH C, WANG Y K. Fundamentals of a Vector Form Intrinsic Finite Element: Part Ⅰ: Basic Procedure and a Plane Frame Element[J]. Journal of Mechanics, 2004, 20(2): 113-122.

[16]DENG H Q, LI T J, WANG Z W, et al. Pretension Design of Space Mesh Reflector Antennas Based on Projection Principle[J]. Journal of Aerospace Engineering, 2015, 28(6): 04014142.