二维重力数据径向反演及应用

林宝泽　肖　锋　王明常

(吉林大学地球探测科学与技术学院，吉林长春 130000)

1　引言

地球物理的反演问题主要包含两个方面：一是地质体的几何参数反演[1,2]； 二是地质体的物性参数反演[3,4]。针对地质体的几何参数反演，建模一般分为三个方案：一是将场源表示为一系列垂直并列仅厚度未知的棱柱体[5-8]； 二是将场源表示为顶点坐标未知的多边形或多面体[9-12]； 三是将包含场源的地下空间剖分成尺寸已知而密度未知的基本矩形单元[13-15]。

径向反演是一种最早由Silva等[16]提出的场源几何参数反演方法； 贾真[17]研究了基于二维模型的重磁梯度分量径向反演算法； Vanderlei等[18,19]将径向反演方法扩展至重力异常的三维反演以及重力梯度张量的三维联合反演。

建模对反演来说至关重要，模型过于复杂会导致解的不稳定性，可以通过Tikhonov正则化方法引入约束条件解决这一问题。径向反演的优点在于将多边形顶点位置用极坐标表示，反演参数(即多边形各顶点对应的半径)具有同一量纲且反演参数相对于直角坐标系减少一半。利用Tikhonov正则化引入相关约束条件(场源几何形态等先验信息)时能取得较好的效果。

径向反演方法虽然已经发展得较为完善，但在国内关于该方法的研究和讨论几乎还是空白。此外，该方法的研究多见于模型实验，对于影响反演结果的正则化参数选取更是缺乏讨论。本文介绍了二维径向反演方法的基本原理，且在此基础上将自适应正则化因子选取引入该方法，并将该方法应用到实际资料处理，取得了较好的效果。

2　方法原理

2.1　正演方法

径向模型的中心点O(x0,z0)必须设定在场源内部，并给定径向多边形的顶点数M，将圆周平均分成M份，此时在直角坐标系下，多边形第k个顶点的坐标(xk,zk)可以表示为

(1)

式中：rk为第k个顶点对应的半径;θk为第k个顶点对应的角度(弧度,沿x轴正方向顺时针旋转为正)。模型及参数如图1所示。

图1　径向模型示意图

从图1不难推断，当顶点数M足够大时，径向模型能取得很好的近似效果。但是从式(1)来看，应用径向模型时存在以下限制：一是包含场源的区域必须是单连通域；二是从模型中心点出发的射线与场源轮廓线有且仅有一个交点。

反演过程中均匀多边形截面二维体的重力异常正演采用文献[20]给出的公式

(2)

式中：G为万有引力常数； Δρ为密度差；Rk、Rk+1分别为测点到多边形第k和k+1个顶点的距离；αk、αk+1分别为测点与第k和k+1个顶点连线与水平方向的夹角；φk为多边形第k条边与水平方向的夹角，如图2所示。

图2　多边形截面二度体正演模型示意型图[20]

2.2　约束反演

设重力异常实测数据构成的N×1维向量为d,径向多边形各顶点对应的半径构成的M×1维向量为r,由模型r得到的正演重力异常为N×1维向量g(r)。为了保证反演问题的适定性，引入约束条件后，该问题转化为求解最优化问题

minψ=‖d-g(r)‖22+μ(Φ1+Φ2)

(3)

式中

(4)

(5)

(6)

(7)

k=1,2,…,M；j=1,2,…,J

其中：ψ为总目标函数；μ为正则化因子；r0为初始模型多边形截面各顶点对应的半径构成的M×1维向量；Φ1为相对邻近性约束，其作用是使模型r的各个分量彼此趋于一致，但不能单独使用；当W为单位矩阵时，Φ2为绝对邻近性约束，作用是稳定解；当W为非单位矩阵时，Φ2为会聚方向约束，使场源物性沿着某一特定方向集中，本文中将场源质量会聚于某一方向，能起到引入与场源几何形态有关的先验信息和稳定解的作用；βj为指定的会聚方向；J表示会聚方向的总数；ε为较小的正数，与场源最小尺寸和最大尺寸之比有关。显然，相对邻近性约束与会聚方向约束是相互矛盾的，绝对邻近性约束是会聚方向约束的特殊形式。除上述约束条件外，还有不等性约束和凸性约束。不等性约束的表达式为

(8)

不等性约束的作用是限制场源的几何尺寸和保证顶点z坐标为非负。凸性约束就是要在每次迭代中满足

(9)

式中ck为中心点O到半径rk与多边形第k-1、k+1个顶点连线交点之间的距离，如图3所示。

图3　凸性约束示意图

由式(2)可以看出，g(r)是关于r的非线性函数，直接求解式(3)较困难，故采用Gauss-Newton迭代法将该非线性反演问题线性化。因此，在r0处对g(r)进行Taylor展开并取一级近似，则有

=g(r0)+JΔr

(10)

式中J为Jacobi矩阵

(11)

令r=r0+Δr,并将式(10)代入式(3)，则

ψ=‖[d-g(r0)]-JΔr‖22+μ‖B(r0+Δr)‖22+

μ‖WΔr‖22

=μ(WΔr)TWΔr+μ[B(r0+Δr)]TB(r0+Δr)+

{[d-g(r0)]-JΔr}T{[d-g(r0)]-JΔr}

(12)

对式(12)两端求导，可得

2μ(BTBΔr+BTBr0+WTWΔr)

(13)

令上式等于0，则迭代修正量Δr的表达式为

Δr=[JTJ+μ(BTB+WTW)]-1×

{JT[d-g(r0)]-μBTBr0}

(14)

2.3　自适应正则化因子选取

正则化因子是数据拟合泛函和模型约束泛函之间的折衷系数，故它的选取直接影响反演结果。在误差水平未知的情况下，常用的参数选取方法有GCV准则和L曲线准则。但是，对于非线性问题的迭代解法来说，这两种准则不太适用。反演时总是将数据拟合置于优先的地位，而在迭代过程中数据拟合泛函值越来越小，故模型约束泛函在总目标泛函中的权重也必须随之减小，即正则化因子是随着迭代过程衰减的。为了适应复杂的反演情况，正则化因子的调整过程应当与反演计算相联系。采用陈小斌[21]提出的自适应调整方案，其表达式为

(15)

式中：μi为正则化因子经验初值；k为迭代次数；φdf、φmc分别为数据拟合泛函与模型约束泛函。上述正则化因子的选取方式虽然显著加快了收敛速度，但在将数据拟合置于优先地位的情况下，迭代次数过多会导致过拟合，故本文将拟合标准差不再明显改变时对应的迭代次数作为最佳迭代次数，所以当迭代次数达到最佳迭代次数或拟合标准差达到阈值时，迭代中止。

3　岩盖模型实验

采用岩盖模型[17]分析不同约束条件对重力异常反演的影响。在有噪反演中，所有模型数据采用的噪声变化范围是原始异常幅值的±2%。

岩盖模型大致呈菌状穹窿状，伞盖部分沿剖面方向宽约1km，伞柄部分与剖面方向大致成45°向下延伸。观测剖面垂直于模型走向(走向垂直于纸面)，其中心位于伞盖中心正上方，沿剖面方向向两侧各延伸1000m，总长度为2000m，点距为20m，密度差为0.5g/cm3，径向模型参数个数为100，初始正则化因子为0.1，会聚方向由虚线表示，与剖面方向分别成0°、45°、180°，会聚因子ε=0.167。图4～图9为岩盖模型的反演结果。

对比图4与图5、图6与图7、图8与图9可见，随机噪声对反演结果的影响不大。从图4～图7可以看出，绝对邻近约束条件下的反演结果能反映模型上边界的大致范围，但是整体上反映的上边界偏深，对下边界特征则完全没有反映。对比图4与图6、图5与7可见，绝对和相对邻近联合约束下得到的反演结果比绝对邻近约束下得到的结果更光滑，但是整体形态并没有明显变化。从图8与图9可以看出，会聚约束条件下的反演结果较为准确地反映了模型的真实形态，准确的先验信息有助于得到更好的反演结果。

图4　绝对邻近约束下无噪反演结果

图5　绝对邻近约束下有噪反演结果

图6　绝对邻近约束和相对邻近约束下无噪反演结果

图7　绝对邻近约束和相对邻近约束下有噪反演结果

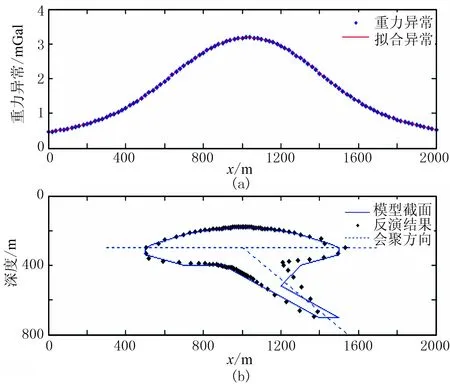
图8　会聚约束下无噪反演结果

图9　会聚约束下有噪反演结果

以上模型实验表明，在会聚方向约束条件下，径向反演方法效果最好；绝对邻近约束条件下，反演结果能大致反映模型的上边界，而下边界总是趋于弧状；相对邻近约束能让绝对邻近约束条件下得到的反演结果更加光滑；凸性约束在控制反演结果的凹凸性上能起到一定的效果。

上文已经提到自适应正则化方法虽然在一定程度上提高了数据拟合度，但是可能会造成过拟合。由于正则化因子伴随着迭代修正不断改变，但不是一味衰减而是伴随着振荡，这也就导致了拟合误差在迭代到一定次数后也会发生振荡。这种振荡可能达到多个数量级，这也就导致了反演结果出现很大的变化，这种变化的好坏是未知的，所以需要确定最优迭代次数。下面的例子仅仅是反演实验中得到的一个特例。

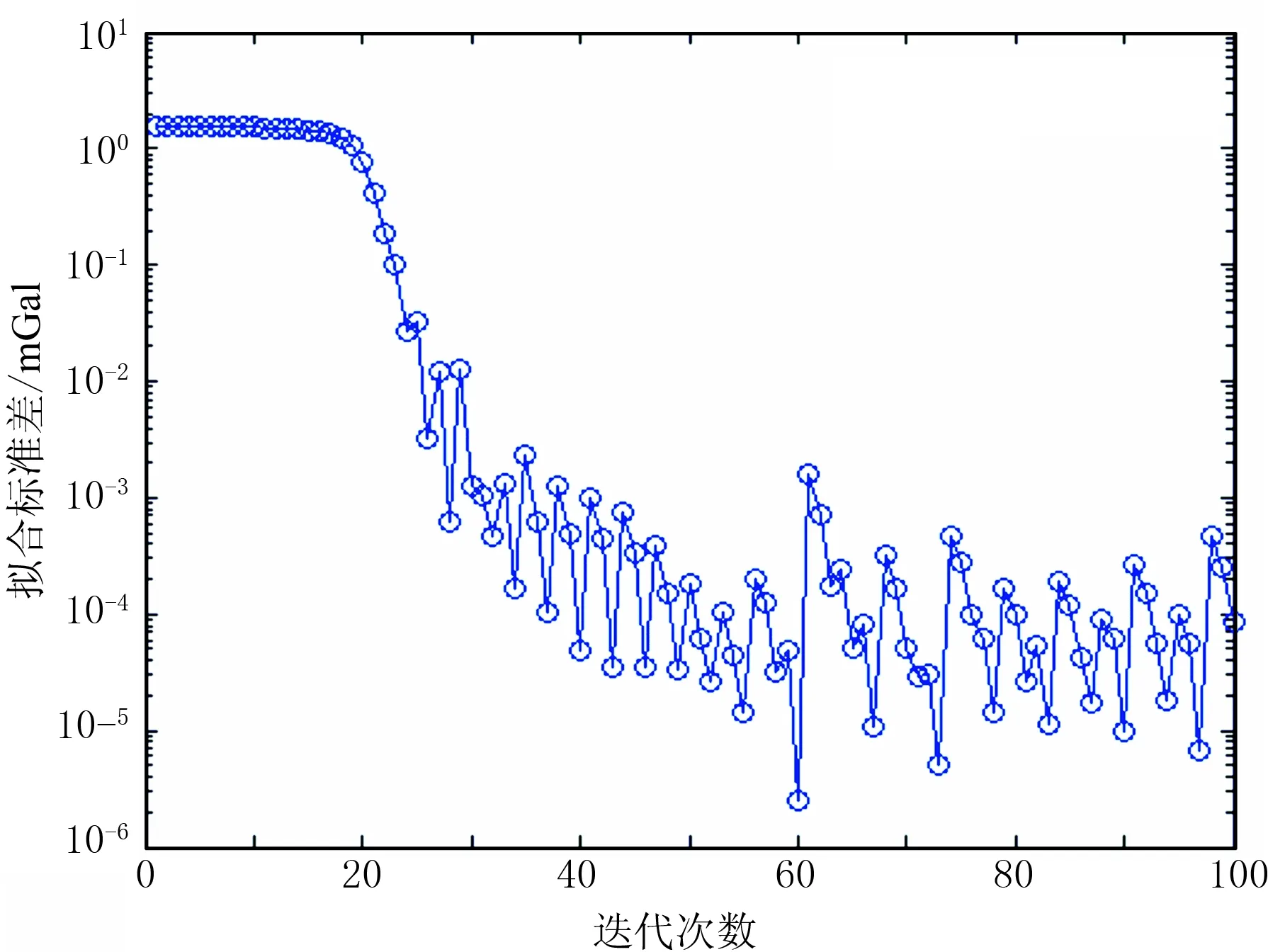
图10　重力异常拟合标准差随迭代次数变化

图11　岩盖模型迭代100次反演结果

图10和图11是绝对和相对邻近联合约束下得到的误差收敛曲线及无噪数据误差收敛曲线和反演结果。在25次迭代之后，拟合误差出现了剧烈振荡。对于迭代100次得到的结果，已经接近于会聚约束下才能得到的结果。但这仅仅是一个特例，笔者认为迭代中止原则还是遵循上文给出的最佳迭代次数原则为宜。

4　应用实例

实际资料选取的是在新墨西哥州里奥格兰德峡谷大桥(图12)上测量得到的重力数据[22]。里奥格兰德峡谷大桥长约400m，高约175m。峡谷周边地层大致可分为三种，分别为玄武岩地层，冲积沉积层，夹杂极薄湖成沉积层，其中玄武岩密度约为2.70g/cm3、沉积岩密度约为2.17g/cm3，具体情况如图12所示。

图12　奥格兰德峡谷大桥截面图

假定峡谷的周边地层的85%为玄武岩、 15%为冲积沉积物，则峡谷与围岩及空气的密度差为-2.62g/cm3。观测剖面长度为800m，点距为20m，径向模型参数个数为40，初始正则化因子为0.1，初始模型半径为25m，会聚因子ε=0.32。反演结果如图13所示。

从图13a中的异常拟合图可见，反演得到的模型正演异常很好地拟合了实测数据。从反演的场源形态看，反演结果较好地反映了场源的深度范围，顶部和左侧较好地反映了场源的边界；右侧底部与实际差异较大， 可能是由于实测异常并不是严格对称的，从而导致反演结果在底部整体向左偏移。借鉴界面反演的相关做法，计算反演多边形的半径各顶点标准差为17.1186m，说明反演结果较可靠。

图13　会聚及凸性约束下反演结果

5　结论

径向反演只能应用于单连通域，且初始模型中心必须位于场源内部。对于不太复杂的单个场源，在利用欧拉反褶积及相关成像等方法得到场源中心近似位置后，利用径向反演可以圈定场源的大致形态；如果能进一步获得关于场源分布的半定量信息，利用会聚约束能得到较好的反演结果。

正则化因子的自适应调整能提高数据拟合精度和收敛速度，但是由于实际数据的复杂性和反演的多解性，片面追求数据拟合效果可能会造成过拟合，利用最佳迭代次数选择原则虽然能解决这一问题，但不可避免地引入人为因素。

此外，由于本文采用的是Gauss-Newton迭代法，故模型初值的选择对反演结果有一定的影响。本方法的初始模型一般采用给定中心埋深的无限长水平圆柱体。在实际数据反演中，地质体中心埋深往往是利用其他方法(如欧拉反褶积、特征点法等)得到的估计值，估计值越接近真实值，最终反演结果精度也越高。采用更加合理、精度更高的计算中心埋深方法与本方法结合将是后续研究的方向。当然，如果有更多的地球物理资料并建立较无限长水平圆柱体更加复杂的初始模型，反演的精度会进一步得到提高。

[1]谷文彬,陈清礼,王余泉等.饶阳凹陷虎8北潜山重力三维松约束反演.石油地球物理勘探,2016,51(6):1219-1226.

Gu Wenbin,Chen Qingli,Wang Yuquan et al.Part-constrained 3D gravity inversion for the Hubabei buried hill in Raoyang Sag.OGP,2016,51(6):1219-1226.

[2]李婧,崔永谦,宋景明等.重力—地震联合建模正演技术在SH地区潜山勘探中的应用.石油地球物理勘探,2016,51(增刊1):152-160.

Li Jing,Cui Yongqian,Song Jingming et al.Gravity forward modeling with model built based on drilling and seismic data:an example of buried hill exploration in Area SH.OGP,2016,51(S1):152-160.

[3]耿美霞,杨庆节.应用RBF神经网络反演二维重力密度分布.石油地球物理勘探,2013,48(4):651-657.

Geng Meixia,Yang Qingjie.2-D density inversion with the RBF neural network method.OGP,2013,48(4):651-657.

[4]王浩然,陈超,杜劲松.重力梯度张量数据的三维反演方法与应用.石油地球物理勘探,2013,48(3):474-481.

Wang Haoran,Chen Chao,Du Jinsong.3-D inversion of gravity gradient tensor data and its applications.OGP,2013,48(3):474-481.

[5]Cordell L and Henderson R G.Iterative three-dimensional solution of gravity anomaly data using a digital computer.Geophysics,1968,33(4):596-601.

[6]Dyrelius D and Vogel A.Improvement of convergence in iterative gravity interpretation.Geophysical Journal of Royal Astronomical Society,1972,27(2):195-205.

[7]Pedersen L B.Interpretation of potential field data - A generalized inverse approach.Geophysical Prospecting,1977,25(2):199-230.

[8]Barbosa V C F,Silva J B C and Medeiros W E.Stable inversion of gravity anomalies of sedimentary basins with non-smooth basement reliefs and arbitrary density contrast variations.Geophysics,1999,64(3):754-764.

[9]Corbato CE.A least-squares procedure for gravity interpretation.Geophysics,1965,30(2):228-233.

[10]Al-Chalabi M.Interpretation of gravity anomalies by nonlinear optimization.Geophysical Prospecting,1972,20(1):1-16.

[11]Moraes R A V and Hansen R O.Constrained inver-sion of gravity fields for complex 3D structures.Geophysics,2001,66(2):501-510.

[12]Wildman R A and Gazonas G A.Gravitational and magnetic anomaly inversion using a tree-based geometry representation.Geophysics,2009,74(3):I23-I35.

[13]Li Y and Oldenburg D W.3-D inversion of gravity data.Geophysics,1998,63(1):109-119.

[14]Portniaguine O and Zhdanov M S.Focusing geophysical inversion images.Geophysics,1999,64(3):874-887.

[15]Silva J B C and Barbosa V C F.Interactive gravity inversion.Geophysics,2006,71(1):1-9.

[16]Silva J B C and Barbosa V C F.Generalized radial inversion of 2D potential field data.Geophysics,2004,69(6):1405-1413.

[17]贾真.均匀二度体位场正演与径向反演方法[学位论文].吉林长春:吉林大学,2009.

Jia Zhen.Forward and Radial Inverse Modeling of Potential Fields Produced by a 2D Homogeneous Source[D].Jilin University,Changchun,Jilin,2009.

[18]Vanderlei C,Oliveira J,Valeria C F et al.Source geo-metry estimation using the mass excess criterion to constrain 3-D radial inversion of gravity data.Geophysical Journal International,2011,187(2):754-772.

[19]Vanderlei C,Oliveira J,Valeria C F et al.3-D radial gravity gradient inversion.Geophysical Journal International,2013,195(2):883-902.

[20]贾真,孟令顺.均匀多边形截面二度体重力异常计算公式的改进.地球物理学进展,2009,24(2):462-467.

Jia Zhen,Meng Lingshun.Some improvements on the formula for calculating the gravity anomaly due to a

2D homogeneous polygonal source.Progress in Geophysics,2009,24(2):462-467.

[21]陈小斌.大地电磁正反演新算法研究及资料处理与解释的可视化集成系统开发[学位论文].北京:中国地

震局地质研究所,2003.

Chen Xiaobin.New Forward and Inversion Algorithms and a Visual Integrated System for MT data [D].Institute of Geology,China Earthquake Administration,Beijing,2003.

[22]Titus W J,Titus S J and Davis J R.A Bayesian approach to modeling 2D gravity data using polygons.Geophysics,2017,82(1):G1-G21.