基于平面波解构的初始波阻抗建模方法

李海山　杨午阳　雍学善

(①中国石油勘探开发研究院西北分院，甘肃兰州 730020； ②CNPC油藏描述重点实验室，甘肃兰州 730020)

1　引言

基于模型的波阻抗反演方法由于具有分辨率高、抗干扰性强等优点，在相关领域得到广泛应用[1-6]。尽管如此，这种方法的反演结果严重依赖于初始模型[7]，因此初始模型的建立至关重要。目前工业界普遍采用的初始模型建立方法是以地震解释层位作为横向控制、以断层和测井资料等作为纵向控制，根据设定的沉积模式将已知属性进行外推内插[8]，这类方法的显著缺点是需要精细的层位和断层解释成果，但在地质构造及沉积关系复杂的区域，往往得不到精细的层位和断层解释结果，且人工解释不但耗时还很容易产生解释误差[9]。

为了克服层位约束建模法的缺陷，有人提出了数据驱动的初始模型建立方法[10-18]，这类方法既不需要耗时的精细层位和断层解释，又充分利用了地震数据本身所隐含的构造和沉积信息。Schultz等[10，11]、Ronen等[12]和Hampson等[13]通过利用地质统计学、多元线性回归或人工神经网络等建立的地震属性与测井信息间的关系获得波阻抗、孔隙度、泥质含量等各种参数模型； Hale[14， 15]提出成像引导的建模方法，通过求解程函方程和混合邻近插值方程得到符合地质规律的参数模型； 刘贤红等[16]提出基于地震属性约束的初始波阻抗模型建立方法，在纵向上利用地震波形相关分析寻找最优插值点，在横向上将地震资料的振幅、波形相关系数等地震属性转换为权系数进行插值建模； Fomel[17]和Karimi等[ 18]提出基于地震数据的预测充填建模方法，该方法首先利用平面波解构法(plane-wave destruction，PWD)[19， 20]计算得到分别沿着纵测线和联络测线方向的同相轴局部斜率，然后根据同相轴局部斜率将井点的信息延拓到整个三维空间。

平面波解构最初是由Claerbout[21]在1992年提出的，由于基于平面波解构的方法具有简单快速、计算精度高、稳定可靠的优点，目前已经广泛地应用于地震资料处理、成像、解释、反演等各个方面[22-24]。本文受Fomel[17]和Karimi等[ 18]研究工作的启发，在对平面波解构进行深入研究的基础上，提出了基于平面波解构的初始波阻抗建模方法。首先利用平面波解构法计算得到地层局部斜率，接着利用平面波解构方程所隐含的道与道之间的预测关系，从井点位置开始进行波阻抗信息的延拓。考虑到直接进行计算的不适定性，在具体计算时，引入Tikhonov正则化方法提高延拓算法的稳定性及抗噪性。模型数据测试及实际资料应用证明了本文方法的有效性，利用本文方法建立的初始波阻抗模型与地震记录所反映的地质规律具有较好的一致性，克服了层位约束建模法容易产生的局部地质现象与解释层位不匹配的缺陷。

2　基于PWD的局部斜率计算原理

2.1　平面波解构算子

Claerbout于1992年提出了平面波解构的概念，其主要思想来源于描述地震数据的局部平面波模型[23]。局部平面波微分方程可表示为[19]

(1)

式中：u=u(t,x)为波场；t和x分别为时间和道间距；σ=σ(t,x)为同相轴局部斜率。在斜率为常数的情况下，式(1)的通解可表示为[19]

u(t,x)=f(t-σx)

(2)

其中f(t)代表波场。若斜率σ不依赖于时间t，可将式(2)变换到频率域，其微分方程形式为[19]

(3)

式(3)的通解为[19]

(4)

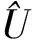
(5)

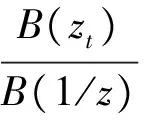
(6)

C(zt,zx)=A(zt,zx)B(1/zt)

=B(1/zt)-zxB(zt)

(7)

式中滤波器B(zt)的系数可以通过在零频率附近进行泰勒级数展开确定，其中通常采用的三点中心滤波器B3(zt)为[19]

(8)

式中的系数分别为

(9)

2.2　局部斜率计算方法

平面波解构算子是一种时空域预测误差滤波器，它通过利用相邻地震道预测当前地震道的方法估算同相轴局部斜率，其预测准则是原始地震道与预测出的地震道之间的残差能量最小。如果用C(σ)表示滤波器C(zt,zx)在时间域与地震数据u(t,x)进行二维褶积运算的算子，则局部平面波微分方程式(1)的隐式有限差分形式为

C(σ)u≈0

(10)

在最小平方意义下，局部斜率σ的估算可转化为求解最小二乘目标函数[19]

(11)

由式(9)可知最优化问题(式(11))是局部斜率σ的非线性优化问题，用高斯—牛顿法(式(11))可转化为[19]

C′(σ0)Δσu+C(σ0)u≈0

(12)

式中： Δσ为斜率增量；σ0为初始斜率；C′(σ)为C(σ)对σ的偏导数。求解式(12)后，初始斜率σ0通过加上斜率增量Δσ得到更新； 然后循环迭代求解式(12)。该方法需要数次非线性迭代获得期望的局部斜率估计，收敛速率依赖于给定的起始斜率值。为了提高计算方法对噪声的抑制能力以及计算结果的连续性，在局部斜率更新过程中，可引入预条件方法[19， 22]

εDΔσ≈0

(13)

式中：ε为常系数扰动因子；D为预条件算子。

3　基于PWD的初始波阻抗建模原理

3.1　初始波阻抗建模原理

计算得到同相轴局部斜率之后，就可以利用平面波解构滤波器通过已知道的波阻抗值预测相邻道的波阻抗值。如果采用式(9)给出的三点中心滤波器系数，则式(10)可写成矩阵方程形式

C1ux-C2ux-1≈0

(14)

式中

(15)

(16)

ux=[u(1,x)u(2,x)u(3,x)…u(T,x)]T

(17)

ux-1=[u(1,x-1)u(2,x-1)u(3,x-1)…u(T,x-1)]T

(18)

式(15)～式(18)中T为最大的时间采样点数(1≤t≤T)，系数

(19)

根据式(14)，如果由x道预测x-1道，则

(20)

如果由x道预测x+1道，则

(21)

根据式(20)和式(21)，如果利用钻井所在位置x道的波阻抗值，就可计算得到相邻的x-1道和x+1道的波阻抗值，依此类推，就可得到整个剖面的波阻抗值。如果有多口井资料，可利用如反距离加权等方式得到多口井约束的建模结果。

3.2　Tikhonov正则化

为方便表述，将式(20)和式(21)用如下的形式统一表示

Cu≈w

(22)

根据矩阵的奇异值分解理论，式(22)中的稀疏矩阵C可分解为列正交矩阵S、元素大于或等于零的对角矩阵Σ和正交矩阵V的转置的乘积，即稀疏矩阵C可表示为

(23)

其中左奇异向量st和右奇异向量vt分别为矩阵S和V的正交列向量，奇异值满足λ1≥λ2≥…≥λT。式(22)的最小二乘解可以表示为

(24)

由于稀疏矩阵C可能为病态矩阵，存在较小的接近于零的奇异值，用式(24)直接求解式(22)可能会使所求解远远偏离原始问题的真解。对于这种不适定问题的求解，需要采用有效的正则化方法。其中Tikhonov正则化法是最著名的一种[25，26]，其基本思想是将解的范数最小作为约束条件加入到原问题中，将原问题转化为在数据拟合程度和解范数最小之间达到某种平衡的问题，该问题即如下最小化问题

(25)

式中μ为正则化参数。根据矩阵C的奇异值分解，正则化参数μ对应的正则化解为

(26)

4　模型数据测试

为说明基于平面波解构的初始波阻抗建模方法的性能，下面用模型数据进行测试。图1a为利用部分Marmousi 2模型得到的二维纵波合成地震记录； 图1b为利用平面波解构法得到的局部斜率场，负值表示局部同相轴向左倾斜，正值表示局部同相轴向右倾斜(图中转换成了倾角，倾角θ与斜率σ的关系为θ=arc tanσ)。由于图1a中的地震反射同相轴相对比较平缓，图1b中大部分斜率值都接近于零，在局部位置出现了相对较大的斜率值，整体上与合成地震记录对应关系良好。

图1c为采用Jason软件建立的初始阻抗模型，建模时以由图1a解释得到的从浅到深的23个层位作为横向控制，以图中黑色曲线所示的纵波阻抗曲线作为纵向控制； 图1d为采用本文方法建立的初始波阻抗模型，建模时采用图1b所示的局部斜率场，以图中黑色曲线所示的纵波阻抗曲线作为已知的道向两边的道进行递推计算。 由图1c和图1d可见，尽管本文方法建立的初始波阻抗模型在远离已知点处准确性略有降低，但整体上与合成地震记录所反映的地质规律具有较好的一致性，且不需要像Jason软件那样费时的精细层位解释。

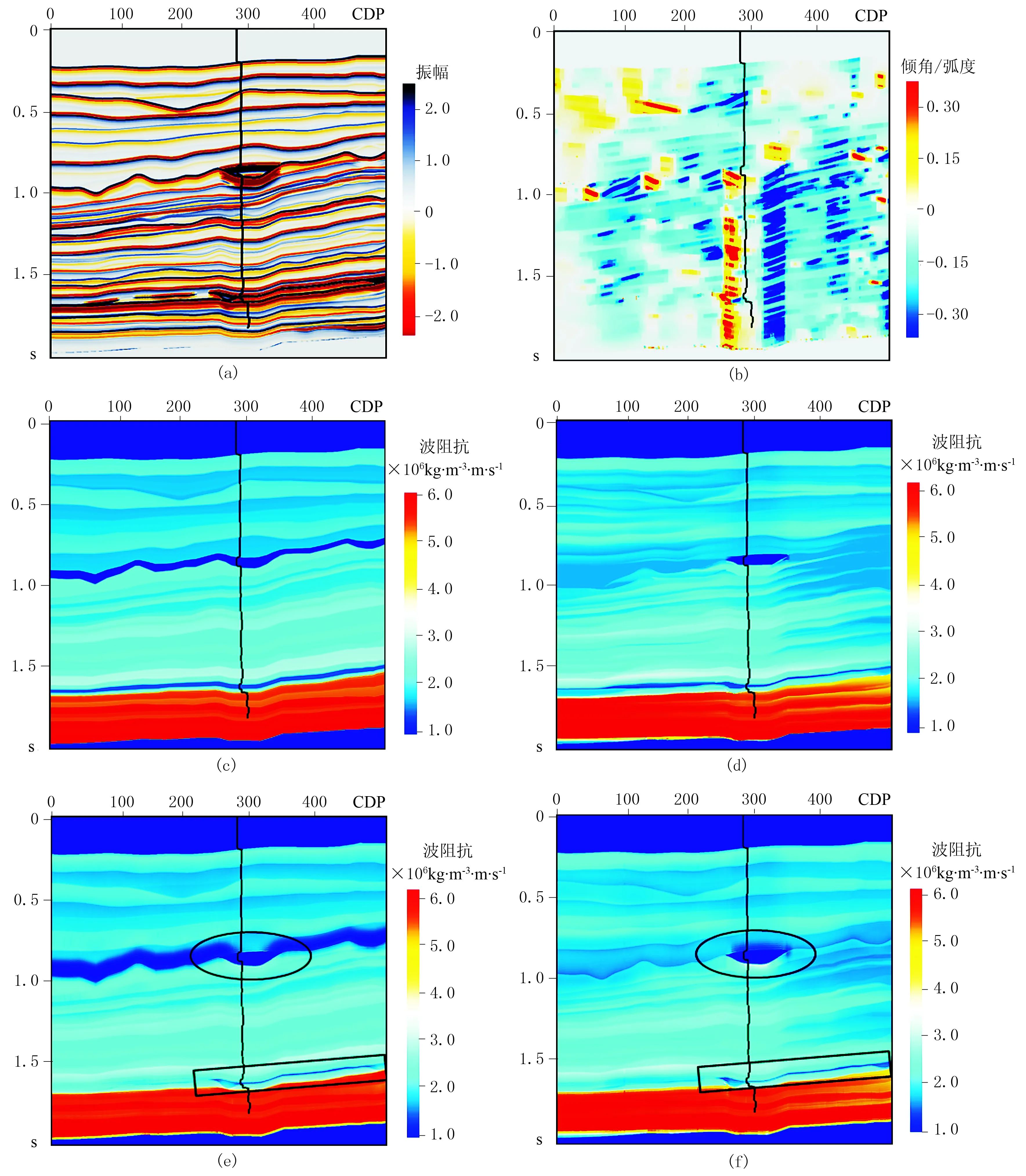
图1　模型数据测试结果比较

图1e为利用Jason软件建立的初始阻抗模型反演得到的结果；图1f为利用本文方法建立的初始波阻抗模型反演得到的结果。从反演结果可见，图中黑色椭圆内的低阻气藏及黑色矩形内的低阻油藏在两种初始模型的反演结果上都得到了准确的刻画，且本文方法反演结果在局部细节上的刻画能力优于Jason软件反演结果，这充分说明了本文方法的有效性和优越性。

5　实际资料应用

为进一步说明本文初始波阻抗建模方法的性能，将本文方法应用于实际资料的建模和反演中。图2a为M油田的叠后地震记录，在CDP314处有一口生产井，图中的黑色曲线为该井的纵波阻抗曲线；图2b为利用平面波解构法得到的局部斜率场；图2c为以图2a中红色线所示的两个解释层位作为横向控制，以井点的纵波阻抗曲线作为纵向控制，采用与层位顶、底平行的沉积模式，由Jason软件建立的初始阻抗模型；图2d为采用本文方法建立的初始波阻抗模型；图2e为利用Jason软件建立的初始阻抗模型反演得到的结果；图2f为利用本文方法建立的初始波阻抗模型反演得到的结果。

由图2c可见，由于解释层位较少，采用简单的沉积模式很难反映目的层内的真实地质规律，因此用Jason软件建立的初始波阻抗模型很容易出现穿时现象，初始模型不能客观地反映地下地质规律。而由图2d可见，本文初始波阻抗建模方法由于是沿着局部同相轴倾斜方向延拓井点的波阻抗值，能够得到与地震记录所反映的地质规律高度一致的结果。由图2e和图2f可见，尽管利用两种不同的初始模型都准确地反演出了图中黑色椭圆内的低阻气藏，但在远离井点(红色箭头所指)位置，利用Jason软件建立的初始阻抗模型反演得到的结果模型化现象严重，可靠性远地低于利用本文方法建立的初始波阻抗模型反演得到的结果。

图2　实际资料应用结果比较

6　结论

(1)本文首先利用平面波解构法计算得到地层局部斜率，接着利用平面波解构方程所隐含的道与道之间的预测关系进行波阻抗信息的空间延拓，并引入Tikhonov正则化方法来提高延拓算法的稳定性及抗噪性，实现了基于平面波解构的初始波阻抗建模方法。

(2)本文方法充分利用了地震数据中所包含的构造和沉积信息，不再像传统建模方法那样需要精细的层位及断层解释结果，直接利用地震数据和测井信息进行初始模型的建立。模型数据测试及实际资料应用证明了本文方法的有效性。

(3)本文方法建立的初始波阻抗模型与地震相变化具有较好的一致性，克服了由于地震层位解释不准确以及地层与解释层位关系复杂造成的模型偏差现象，是对层位约束建模方法的一种补充和完善，通过优化完善并推广到三维初始模型的建立，具有广阔的应用前景。

[1]Gray D,Goodway B and Chen T.Bridging the gap：Using AVO to detect changes in fundamental elastic constants.SEG Technical Program Expanded Abstracts,1999,18：852-855.

[2]Downton J E,Lines L R.Constrained three parameter AVO inversion and uncertainty analysis.SEG Technical Program Expanded Abstracts,2001,20：251-254.

[3]Russell B H,Hedlin K,Hilterman F J et al.Fluid-property discrimination with AVO：A Biot-Gassmann perspective.Geophysics,2003,68(1)：29-39.

[4]杨培杰,印兴耀,张欣.叠后地震盲反演及其应用.石油地球物理勘探,2008,43(3)：284-290.

Yang Peijie,Yin Xingyao and Zhang Xin.Poststack seismic blind inversion and application.OGP,2008,43(3)：284-290.

[5]赵小龙,吴国忱,曹丹平.多尺度地震资料稀疏贝叶斯联合反演方法.石油地球物理勘探,2016,51(6)：1156-1163.

Zhao Xiaolong,Wu Guochen,Cao Danping.A sparse Bayesian joint inversion of multi-scale seismic data.OGP,2016,51(6)：1156-1163.

[6]张丰麒,金之钧,盛秀杰等.一种稳健的弹性阻抗反演方法.石油地球物理勘探,2017,52(2)：294-303.

Zhang Fengqi,Jin Zhijun,Sheng Xiujie et al.A stable elastic impedance inversion approach.OGP,2017,52(2)：294-303.

[7]朱勇,唐斌.一种提高波阻抗反演建模精度的方法.江汉石油职工大学学报,2017,20(6)：22-26.

Zhu Yong and Tang Bin.A method of improving modeling precision of wave impedance inversion.Journal of Jianghan Petroleum University of Staff and Workers,2017,20(6)：22-26.

[8]夏洪瑞,周开明,黄桥.波阻抗反演中的一种建模方法.石油物探,2004,43(1)：30-32.

Xia Hongrui,Zhou Kaiming and Huang Qiao.Building of initial model for wave impedance inversion.GPP,2004,43(1)：30-32.

[9]王伟,郭宇宏,高静怀等.基于高精度地层倾角线性反演的地震全体积拉平方法.地球物理学报,2013,56(3)：1012-1022.

Wang Wei,Guo Yuhong,Gao Jinghuai et al.Volumetric flattening through linear inversion scheme with accurate seismic dips.Chinese Journal of Geophysics,2013,56(3)：1012-1022.

[10]Schultz P S,Ronen S,Hattori M et al.Seismic-guided estimation of log properties,part 1：A data-driven interpretation methodology.The Leading Edge,1994,13(5)：305-310.

[11]Schultz P S,Ronen S,Hattori M et al.Seismic-guided estimation of log properties,part 3：A controlled study.The Leading Edge,1994,13(7)：770-776.

[12]Ronen S,Schultz P S,Hattori M et al.Seismic-guided estimation of log properties,part 2： Using artificial neural networks for nonlinear attribute calibration.The Leading Edge,1994,13(6)：674-678.

[13]Hampson D P,Schuelke J S and Quirein J A.Use of multi-attribute transforms to predict log properties from seismic data.Geophysics,2001,66(1)：220-236.

[14]Hale D.Image-guided blended neighbor interpolation of scattered data.SEG Technical Program Expanded Abstracts, 2009,28：1127-1130.

[15]Hale D.Image-guided 3D interpolation of borehole data.SEG Technical Program Expanded Abstracts,2010,29：1266-1270.

[16]刘贤红,査树贵.地震属性约束初始波阻抗模型建立方法.中国石油学会2010年物探技术研讨会论文集,2010,374-376.

Liu Xianhong and Zha Shugui.Seismic attribute constrained initial wave impedance modeling method.Symposium on Geophysical Prospecting Techniques,Chinese Petroleum Society,2010,374-376.

[17]Fomel S.Predictive painting of 3D seismic volumes.Geophysics,2010,75(4)：A25-A30.

[18]Karimi P and Fomel S.Image guided well log interpolation using predictive painting.SEG Technical Program Expanded Abstracts,2015,34：2786-2790.

[19]Fomel S.Applications of plane-wave destruction filters：Geophysics,2002,67(6)：1946-1960.

[20]Chen Z,Fomel S and Lu W.Accelerated plane-wave destruction.Geophysics,2013,78(1)：V1-V9.

[21]Claerbout J F.Earth Soundings Analysis：Processing Versus Inversion.Blackwell Scientific Publications Inc,1992.

[22]Fomel S.Shaping regularization in geophysical estimation problems.Geophysics,2007,72(2)：R29-R36.

[23]黄建平,李振春,孔雪等.基于PWD的绕射波波场分离成像方法综述.地球物理学进展,2012,27(6)：2499-2510.

Huang Jianping,Li Zhenchun,Kong Xue et al.The review of the wave field separation method about reflection and diffraction based on the PWD.Progress in Geophysics,2012,27(6)：2499-2510.

[24]Gan S,Wang S,Chen Y et al.Deblending using a structural-oriented median filter.SEG Technical Program Expanded Abstracts,2015,34：59-64.

[25]Tikhonov A N and Arsenin V Y.Solutions of Ill-posed Problems.New York：John-Wiley & Sons, 1977.

[26]王治强,曹思远,陈红灵等.基于TV约束和Toepplitz矩阵分解的波阻抗反演.石油地球物理勘探,2017,52(6)：1193-1199.

Wang Zhiqiang,Cao Siyuan,Chen Hongling et al.Wave impedance inversion based on TV regularization and Toeplitz-sparse matrix factorization.OGP,2017,52(6)：1193-1199.