类似于VNL环的环
2018-09-19任艳丽
王 尧,杨 圳,任艳丽
(1.南京信息工程大学数学与统计学院,江苏南京 210044)
(2.南京晓庄学院信息工程学院,江苏南京 211171)
1 引言
本文所研究的环R都是有单位元1的结合环,环同态都是保持单位元不变的.设a∈R是环R中一个元素,称a是(von Neumann)正则的,如果存在b∈R,使得a=aba.如果还满足ab=ba,则称 a 为强正则的.称 a 是弱正则的,如果存在r′,r′′∈ R,使得a=ar′ar′′.称a是π-正则的(强π-正则的),如果存在b∈R和正整数n使得an=anban(an=an+1b).称a是单式正则的,如果存在一个可逆元u∈R使得a=aua.称一个环R是正则(强正则,弱正则,π-正则,强π-正则,单式正则)环,如果R中所有元素都是正则(强正则,弱正则,π-正则,强π-正则,单式正则)元.显然正则环是弱正则环.众所周知,一个环为局部环当且仅当对任意a∈R,a或1−a是可逆的.局部环是环理论中一类极其重要的环,有大量的研究.Contessa[1]拓展局部环的概念,称一个环R是VNL(Von Neumann Local)环,如果对任意a∈R,都有a或1−a是正则的.VNL环是近年来环论研究的热点之一(参见文献[2–5]).此外,Chen[6]称一个环R是几乎单式正则环,如果对任意a∈R,都有a或1−a是单式正则的;称一个环R是几乎强正则环,如果对任意a∈R,a或1−a是强正则的.
本文进一步拓展局部环的概念,在弱正则环、π-正则环、强π-正则环的基础上,分别定义和研究几乎弱正则环、几乎π-正则环、几乎强π-正则环的性质.
2 定义及相关环之间的关系
定义2.1称一个环是几乎弱正则环(几乎π-正则环,几乎强π-正则环),如果对任意a∈R,a或1−a是弱正则(π-正则,强π-正则)的.
由定义知,弱正则环是几乎弱正则环,局部环、几乎强正则环和VNL环都是几乎弱正则环.因此存在以下关系:{局部环}⊆{几乎强正则环}⊆{VNL环}⊆{几乎弱正则环}.
另一方面,VNL环和π-正则环都是几乎π-正则环,几乎强正则环和强π-正则环都是几乎强π-正则环,几乎强π-正则环是几乎π-正则环.在文献[7]中,几乎π-正则环和几乎强π-正则环被称作局部π-正则环和局部强π-正则环,其中的命题3.2.16证明:在Abel环条件下,几乎强π-正则环与几乎π-正则环是等价的.
下面的例子说明,几乎弱正则环是弱正则环概念的真推广.
例 2.2 设 Z4={,,,} 是整数环模理想 (4)的商环,它是几乎弱正则环但不是弱正则环.事实上,,,都是正则元,−是正则元,因此 Z4是几乎弱正则环.但不是弱正则的,因此Z4不是弱正则环.
称一个环R是双正则的,如果R的每个主理想都是由一个中心幂等元生成的.由文献[8]中结论,双正则环是弱正则环.下面的例子说明几乎弱正则环是VNL环概念的真推广,几乎强π-正则环是强π-正则环的真推广.
例2.3 (1)[9]设R是VNL环但不是双正则环,S是双正则环但不是VNL环,则R⊕S是几乎弱正则环,但它既不是VNL环也不是双正则环.
(2)[7]设p是任一素数,R=Zp={m/n;m,n∈Z,(n,p)=1}是Z在P处的局部化,则R是局部环,因此也是几乎强π-正则环.但因为p∈R不是R的π-正则元素,所以R不是强π-正则环.
下面的例子说明,几乎π-正则环是π-正则环与VNL环概念的真推广.
例2.4设Z4⊕ Z4. 易证 (,),(,)− (,) 都不是正则的,因此 R 不是 VNL 环.因为R是π-正则环,因此也是几乎π-正则环.
例2.5令R=R1×R2,其中R1是π-正则环但不是VNL环,R2是VNL环但不是π-正则环.显然R既不是π-正则环也不是VNL环.但R是几乎π正则环.
证 因为对任意的(a,b)∈R,其中a∈R1,b∈R2,由R2是VNL环,则b或1−b是正则的.如果b正则的,则b是π-正则的,所以(a,b)是π-正则元素.如果1−b正则的,则1−b是π-正则的,所以(1−a,1−b)是π-正则元素.所以(a,b)或(1−a,1−b)是π-正则的.所以R是几乎π-正则环,但显然R既不是π-正则环也不是VNL环.
下面举例说明几乎强π-正则环是局部环和强π-正则环的真推广.
例2.6 R=Z4×Z4是强π-正则环,因此也是几乎强π-正则环.但(0,1)2=(0,1)不是平凡的幂等元,所以R不是局部环.
例2.7令R=C×D,其中C是强π-正则环但不是几乎强正则环,D是几乎强正则环但不是强π-正则环.显然R既不是强π-正则环也不是几乎强正则环.但R是几乎强π-正则环.证明类似例2.5.
下面的例子说明几乎π-正则环是几乎强π-正则环的真推广.
例 2.8 设 Z6={,,,,,} 是整数环模理想 (6) 的商环, 它是正则环. 由文献[4,定理2.3]知R是正则环当且仅当Mn(R)是VNL环,对于n≥2.因此M2(Z6)是VNL环.因此也是几乎π-正则环.经过计算可以验证,在M2(Z6)中,矩阵和都不是强π-正则的.因此M2(Z6)不是几乎强π-正则环.
综上,得到相关环的如下关系图.

命题2.9对任意的交换环R,以下命题等价:
(1)R是VNL环;
(2)R是几乎强正则环;
(3)R是几乎弱正则环.
证 显然.
命题2.10(1)几乎弱正则环R的中心C(R)是VNL环;
(2)几乎π-正则环R的中心C(R)是几乎强π-正则环.
证 (1)对任意x∈C(R),x或1−x是R中弱正则元,如果x在R中弱正则,则存在r′,r′′∈ R 使得 x=xr′xr′′=x2r′r′′∈ x2R. 由文献 [9]命题 12,可以推出 x=x(xky)x,其中y∈R,k≥1.而且,对任意r∈R,

即xky∈C(R).所以x是C(R)中正则元.同理,如果1−x是R中弱正则元,可以推出1−x也是C(R)中正则元.所以R的中心C(R)是VNL环.
(2)证明见文献[7]命题3.2.17.
一个环R称为Abel环,如果R中幂等元都是中心幂等元.文献[7]的命题3.2.12和文献[10]的推论3证明:如果R是几乎π-正则环(几乎强π-正则环),则对任意e=e2∈R,eRe也是几乎π-正则环(几乎强π-正则环).
命题2.11如果R是Abel几乎弱正则环,则对任意e=e2∈R,eRe也是几乎弱正则环.
证 对于a∈eRe,存在r∈R使得a=ere,于是有ea=ae=eae=a.因为R是几乎弱正则环,所以a或1−a是R中弱正则元.若a是弱正则的,则存在b′,b′′∈R,使得a=ab′ab′′=(ae)b′(eae2)b′′=a(eb′e)a(eb′′e),其中 eb′e,eb′′e ∈ eRe,所以 a 在 eRe 中弱正则.若 1− a 在 R 中弱正则,则存在 c′,c′′∈ R 使得 1− a=(1− a)c′(1− a)c′′. 由此可得e− a=e(1 − a)e=e(1 − a)c′(1 − a)c′′e=(e− a)ec′e(e− a)ec′′e,其中 ec′e,ec′′e ∈ eRe. 所以1−a在eRe中弱正则.这证明了eRe是几乎弱正则环.
引理2.12设A=diag{a1,a2,···,an}是主对角线元素为ai,其余位置都是0的n×n阶矩阵.在Mn(R)中,A=diag{a1,a2,···,an}弱正则当且仅当a1,···,an都在R 中弱正则.
定理2.13 设R是一个环,以下命题等价:
(1)R是弱正则环;
(2)对于每一自然数n,Mn(R)是几乎弱正则环.
证 (1)⇒(2).由文献[11]引理1.1,R是弱正则环可以得到Mn(R)是弱正则环,因此也是几乎弱正则环.
(2)⇒(1).对任意a∈R,取A=diag{a,1−a,1,···,1}∈Mn(R),In是Mn(R)中单位矩阵.从而In−A=diag{1−a,a,0,···,0}因为Mn(R)是几乎弱正则环,所以A或In−A在Mn(R)中是弱正则的.由引理2.12知无论A或In−A是弱正则的,均可以得到a在R中弱正则.因此R是弱正则环.
命题2.14(1)单环都是几乎弱正则环;
(2)如果环R的每个右理想都是由幂等元生成的,则R是几乎弱正则环.
证 由文献[8,命题4.7]知单环是弱正则环;如果环R的每个右理想都是由幂等元生成的,则R是弱正则环.因此,它们都是几乎弱正则环.
文献[12]中称一个环R是ELT环,如果R中每个本质左理想都是理想.
命题2.15设R是ELT环,以下命题等价:
(1)R是几乎弱正则环;
(2)R是VNL环.
证 (2)⇒(1)显然成立.
(1)⇒ (2).构造这样一个本质左理想I=(a〉⊕PLi,其中(a〉是R中由a生成的主左理想,Li是R中所有不含a的左理想.由R是ELT环知I是R的理想.因为R是几乎弱正则环,对任意a∈R,有a或1−a弱正则.如果a是弱正则的,则存在x′,x′′∈ R 使得 a=ax′ax′′∈ aRaR ⊆ aI. 于是存在 b ∈ R,l∈ Pli使得 a=a(ba+l),a−aba=(1−ab)a∈ (a〉.另一方面,a−aba=al∈ PLi,而(a〉TPLi=0,这推出a=aba,所以a在R中是正则的.如果1−a是弱正则的,类似可证1−a是正则的.综上,R是VNL环.
引理2.16[8]对于一个约化环R以及a∈R,有
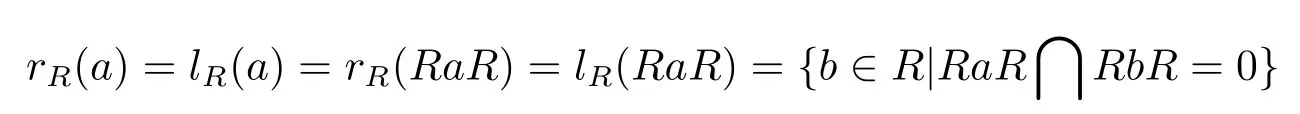
是R的一个理想I,且ITRaR=0,其中lR(a),rR(a)分别表示环R中a的左、右零化子集合.
定义2.17称一个环是几乎双正则环,如果对任意x∈R,RxR或R(1−x)R是由中心幂等元生成的.
命题2.18设R是约化环,则以下命题等价:
(1)R是几乎弱正则环;
(2)R是几乎双正则环.
证 (2)⇒ (1).对于a∈R,RaR或R(1−a)R是由中心幂等元生成的.如果RaR是由中心幂等元生成的,则存在一个中心幂等元e∈R使得RaR=(e),从而aR=aRe⊆aR(RaR)=(aR)2⊆aR,因此a在R中是弱正则的.如果R(1−a)R是由中心幂等元生成的,同理可以得到1−a在R中是弱正则的.
(1)⇒(2).对于a∈R,由假设知a或1−a是弱正则的.如果a在R中弱正则,记rR(a)=B,由引理2.16知B=rR(a)=rR(RaR)=lR(RaR)且BTRaR=0.因为a是弱正则的,所以存在b∈RaR使得a=ab,因此有a−ab=0,a(1−b)=0,1−b∈rR(a),因此RaR+B=R.又因为BTRaR=0,从而有RaR⊕B=R.由文献[13]引理4知,RaR是由中心幂等元生成的.如果1−a在R中弱正则,同理可得R(1−a)R是由中心幂等元生成的.
命题2.19约化的几乎强π-正则环是VNL环.
证 任取x∈R,因为R是几乎强π-正则环,则x或1−x是强π-正则的.假定x是强π-正则的,则存在z∈R和正整数n使得xn=xn+1z,xz=zx.设e=xnzn.因为xn=xn+1z=xn+2z2=···=x2nzn=xnznxn.因此e2=e,x与1−e可交换,
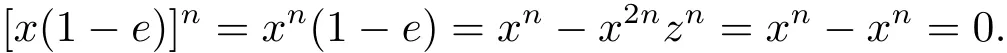
又因为R是约化环,从而有
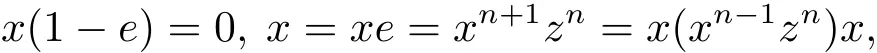
即x是正则的.假定1−x是强π-正则的,类似可得1−x也是正则的.所以R是VNL环.
命题2.20设环T=S+K,其中S是T的子环,K是T的幂零理想,则T是几乎强π-正则环当且仅当S是几乎强π-正则环.
证 假定Kn=0,对于特定的n≥1.
(⇐=)任取t∈T,t=s+x其中s∈S,x∈K.因为S是几乎强π-正则的,有s或1−s是强π-正则的.如果s是强π-正则的,则存在k≥1使得skS=sk+1S=···,因此存在s0∈S使得sk=snk+1s0.于是有tk=(s+x)k=sk+x0=snk+1s0+x0tnk+1=(s+x)nk+1=snk+1+x1,其中x0,x1∈K.这样,tk−tnk+1s0=x0−x1s0∈K.因为Kn=0,(tk−tnk+1s0)n=0,从而得到tnk∈tnk+1T,所以t在T中是强π-正则的.如果1−s是强π-正则的,同理可证1−t是强π-正则的.所以T是几乎强π-正则环.
(=⇒)任取s∈S.因为T是几乎强π-正则的,有s或1−s在T中是强π-正则的.如果s是强π-正则的,则存在k≥ 1使得skT=sk+1T= ···,因此存在t∈T,sk=snk+1t.令t=a+x,其中a∈S,x∈K.这样就有sk−snk+1a=snk+1x∈K,Kn=0,(sk−snk+1a)n=0,从而有snk∈snk+1S,所以s在S中是强π-正则的.如果1−s在T中是强π-正则的,同理可证1−s在S中也是强π-正则的,即S是几乎强π-正则环.
文献[12]中称环R的右理想I为广义弱理想(GW理想),如果对任意a∈I,存在一个正整数n,使得Ran⊆I.
命题2.21设环R中的极大右理想都是GW理想,则以下命题等价:
(1)R是几乎强正则环;
(2)R是几乎弱正则环.
证 (1)⇒(2)由定义可得.
(2)⇒(1).因为R是几乎弱正则环,对于任意a∈R,有a或1−a弱正则.如果a是弱正则的,则存在s,t∈R使得a=asat.假设r(a)+aR≠R且M 是R中包含r(a)+aR的极大右理想,则由a(1−sat)=0知1−sat∈r(a)⊆M.如果sat/∈M,则有M+satR=R,且存在x∈M,r∈R使得x+satr=1.因为M 是GW理想且atrs∈M,故存在一个正整数n使得s(atrs)n∈M,于是有(1−x)n+1=(satr)n+1=s(atrs)natr∈M.又因为x∈M,从而有1∈M,这与M≠R矛盾.因此必有sat∈M,从而得到1∈M,此为矛盾.所以假定不成立,有r(a)+aR=R,因此a在R中是强正则的.如果1−a在R中是弱正则的,利用上述方法可以得到1−a在R中是强正则的.综上,R是几乎强正则环.
3 更多的例子
命题3.1几乎弱正则环(几乎π-正则环,几乎强π-正则环)的同态像还是几乎弱正则环(几乎π-正则环,几乎强π-正则环).
证 设R是几乎弱正则环,σ:R→ R′是一个环同态.对任意a∈R,有a或1−a是弱正则的. 如果 a是弱正则的,则存在 r′,r′′∈ R 使得 a=ar′ar′′. 于是有σ(a)= σ(ar′ar′′)= σ(a)σ(r′)σ(a)σ(r′′),所以 σ(a) 是 R′中弱正则元. 同理可证,如果 1 − a是R中弱正则元,则1−σ(a)是R′中弱正则元.因此R′也是几乎弱正则环.对于几乎π-正则环与几乎强π-正则环的情况,类似可证.
定理3.2(1)一族环的直积∏{Rα:α∈I}是几乎弱正则环当且仅当存在α0∈I使得Rα0是几乎弱正则环,其余α∈I−α0,Rα均为弱正则环.
(2)一族环的直积∏{Rα:α∈I}是几乎π-正则环当且仅当存在α0∈I使得Rα0是几乎π-正则环,其余α∈I−α0,Rα均为π-正则环.
(3)一族环的直积∏{Rα:α∈I}是几乎强π-正则环当且仅当存在α0∈I使得Rα0是几乎强π-正则环,其余α∈I−α0,Rα均为强π-正则环.
证 (1)充分性.显然成立.
必要性.假定∏{Rα:α∈I}是几乎弱正则环.因为Rα是∏Rα的同态像,由命题2.1知每个Rα都是几乎弱正则环.任取一α0∈I,记∏{Rα:α∈I}=Rα0×S,其中S=∏{Rα:α∈I−α0}.如果Rα0与S都不是弱正则环,则存在非弱正则元r∈Rα0,s∈S.取a=(r,IS−s),则在∏{Rα:α∈I}中,a或1−a都不是弱正则的,得到矛盾.因此,Rα0或S必有之一是弱正则的.如果S是弱正则的,则定理得证.如果S是几乎弱正则环,则重复以上讨论,可得结论.
(2)和(3)的证明与(1)类似.
推论3.3如果R=S×T是几乎弱正则环(几乎π-正则环,几乎强π-正则环),则S和T一个是几乎弱正则环(几乎π-正则环,几乎强π-正则环),另一个是弱正则环(π-正则环,强π-正则环).
两个几乎弱正则环的直积未必是几乎弱正则环.由例2.2,Z4是几乎弱正则环,但Z4×Z4不是几乎弱正则环.这是因为,取 a=(,),1 − a=(,),则在 Z4× Z4中,a 或者 1 − a 都不是弱正则的.
设D 是环C的一个子环,且1c∈D,则
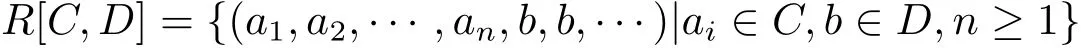
在普通的加法和乘法定义下构成一个环.
定理3.4下面两个命题等价:
(1)R[C,D]是几乎弱正则环(几乎π-正则环,几乎强π-正则环);
(2)C是弱正则环(π-正则环,强π-正则环)且D 是几乎弱正则环(几乎π-正则环,几乎强π-正则环).
证 (1)⇒ (2).设 ϕ :R[C,D]→ D,ϕ(a1,a2,···,an,b,b,···)=b.易见 ϕ 是一个环同态.由命题3.1知D是几乎弱正则环.假定C不是弱正则环,则存在x∈C不是弱正则元.取 a=(x,1−x,1,1,···)∈ R[C,D],有 1−a=(1−x,x,0,0,···).由于 R[C,D]是几乎弱正则环,则a或1−a在R[C,D]中是弱正则的.如果a是弱正则的,则x∈C是弱正则的,矛盾.若1−a是弱正则的,则也有x∈C是弱正则的,矛盾.所以假设不成立,C是弱正则环.
(2)⇒ (1).对任意 (a1,a2,···,an,b,b,···)∈ R[C,D],其中 ai∈ C,b∈ D.因为 C 是弱正则环,所以存在使因为D 是几乎弱正则环,则b或1−b是D中弱正则元.如果 b是弱正则元,则存在 y′,y′′∈ D 使得 b=by′by′′.因此有

这表明(a1,a2,···,an,b,b,···)是R[C,D]中弱正则元.如果1−b是D 中弱正则元.同理可证1−(a1,a2,···,an,b,b,···)是R[C,D]中弱正则元.综上知R[C,D]是一个几乎弱正则环.
对于几乎π-正则环和几乎强π-正则环的情况,类似可以证明.
设R是一个环,RVR是一个双模,且V是一个一般环(未必有1).称环I(R;V)=R⊕V是环R关于V的理想扩张,其中加法是通常的加法,乘法运算定义为(r,v)(s,w)=(rs,rw+vs+vw).
命题3.5如果环R关于V的理想扩张S=I(R;V)是几乎弱正则环(几乎π-正则环,几乎强π-正则环),则R是几乎弱正则环(几乎π-正则环,几乎强π-正则环).
证 因为S=I(R;V)是几乎弱正则环,所以对任意(r,v)∈I(R;V),(r,v)或(1,0)−(r,v) 是弱正则的. 若 (r,v) 是弱正则元,则存在 (x′,y′),(x′′,y′′) ∈ I(R;V) 使得 (r,v)=(r,v)(x′,y′)(r,v)(x′′,y′′). 这推出 r=rx′rx′′,r 在 R 中是弱正则的. 若 (1,0)− (r,v) 是弱正则的, 则存在 (x′,y′),(x′′,y′′) ∈ I(R;V) 使得 (1 − r,−v)=(1 − r,−v)(x′,y′)(1 −r,−v)(x′′,y′′),于是有 1 − r=(1− r)x′(1− r)x′′. 所以 1− r 在 R 中是弱正则的. 综上知 R是几乎弱正则环.
命题3.5的逆命题不成立.例如,环R=Z4是几乎弱正则环,取V=Z4,则S=I(Z4;Z4) 不是几乎弱正则环. 这是因为在 I(Z4;Z4) 中,(,) 不是弱正则的,(,) − (,)也不是弱正则的. 假设 (,) 是弱正则的,则存在 (x′,y′),(x′′,y′′) ∈ I(Z4;Z4) 使得 (,)=于是有这不可能. 所以假设不成立. 另一方面, 对于假设存在使得则有要满足等式成立,则需取此时矛盾. 因此(,)− (,) 也不是弱正则的. 所以 S=I(Z4;Z4) 不是几乎弱正则环.几乎 π -正则环,几乎强π-正则环的情况类似可以证明.
命题3.6(1)如果R是弱正则环,S是局部环,设RMS是一个双模,则是几乎弱正则环.
(2)如果R是π-正则环(强π-正则环),S是局部环,则是π-正则环(强π-正则环).
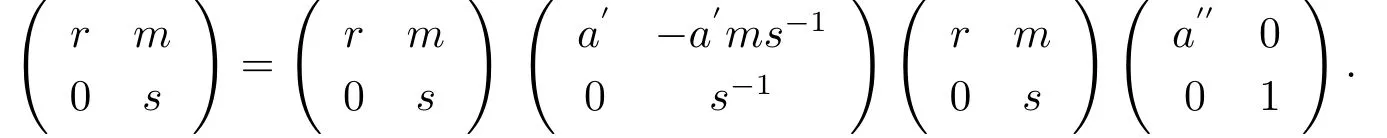
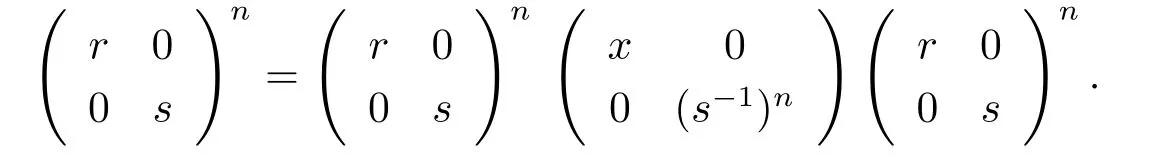
R是强π-正则环的情况类似可证.
命题3.7几乎弱正则环(几乎π-正则环,几乎强π-正则环)的直极限仍是几乎弱正则环(几乎π-正则环,几乎强π-正则环).
证 设{Rα,ϕαβ|α,β∈I}是几乎弱正则环上的直系统,R为Rα的直极限,ηα:Rα→R,α∈I是环单同态,其中Im(ηα)表示单同态ηα的像.下证R 是几乎弱正则的.任取r∈R,存在α∈I,使得r∈Imηα,即存在rα∈Rα,使得ηα(rα)=r,同时有ηα(1Rα−rα)=1R−r.由于Rα是几乎弱正则环,所以rα或1Rα−rα弱正则.如果rα是弱正则的,则存在使得从而有其中即r在R中是弱正则的.同理,如果1Rα−rα是弱正则的,可以得到1R−r在R中是弱正则的.综上知R是几乎弱正则环.
几乎π-正则环,几乎强π-正则环的情况类似可以证明.
