基于深度展开ISTA网络的混合源定位方法

苏晓龙 户盼鹤 刘天鹏 彭勃 程耘 刘振

（国防科技大学电子科学学院，湖南长沙 410073）

1 引言

辐射源定位在无源雷达中发挥着越来越重要的作用［1-2］，在无源雷达探测中［3-4］，空间中辐射源按照与接收阵列的距离可以将分为远场源和近场源［5］，远场源的位置需要由波达方向（Direction of Arrival，DOA）进行描述，而近场源的位置需要由DOA 和距离参数进行描述［6］。随着阵列参数估计技术的发展，嵌套阵列受到了越来越多的关注。嵌套阵列是一种非均匀阵列［7-8］，文献［9］采用嵌套对称阵列实现远场和近场混合源进行定位，相比于均匀线阵，该方法在阵元个数相同的情况下增大了阵列孔径，能够提高混合源的参数估计精度［10］，但是该方法需要计算四阶累积量，运算量较大。文献［11］在嵌套对称阵列下利用卷积神经网络实现近场源定位，相较于传统的模型驱动类方法，该方法不需要对协方差矩阵进行特征值分解，能够减少计算复杂度，但是该方法为“黑箱模型”，网络的参数不具备可解释性，导致泛化能力较差。

近年来，由于深度展开网络同时具有模型驱动类方法和数据驱动类方法的优势，因此受到了国内外学者广泛关注［12-13］。深度展开网络是将迭代压缩感知算法的迭代步骤级联为神经网络层，并利用深度学习的方法对网络进行训练［14-15］。相比于传统深度神经网络的参数，深度展开网络的参数具备可解释性，网络的泛化能力得到提升［16］。文献［17］将迭代收缩阈值算法（Iterative Shrinkage Thresholding Algorithm，ISTA）展开为网络级联形式，实现对远场源DOA 估计。相较于传统的基于机器学习的数据驱动类方法，该方法的网络参数具备可解释性，使得泛化能力得到提高［18-19］，但该方法不能实现近场和远场混合源识别和定位。

针对上述问题，本文提出了一种基于深度展开ISTA 网络的混合源定位方法，该方法通过混合源协方差矩阵差分方法和子空间差分方法分别得到近场源差分向量和远场源协方差向量，并通过深度展开ISTA 网络输出的空间谱对混合源的参数进行估计。

2 混合源数学模型

如图1 所示，对空间中的近场（Near-Field，NF）源进行定位需要对波达方向θNF和距离rNF进行估计，对空间中的远场（Far-Field，FF）源进行定位需要对波达方向θFF进行估计。嵌套对称阵列包括M个阵元，实心点表示第1 级子阵，阵元间距为d，包含M/2个阵元，其阵元位置为：

图1 嵌套对称阵列下近场和远场混合源定位示意图Fig.1 Geometry of nested array with mixed near-field and farfield sources

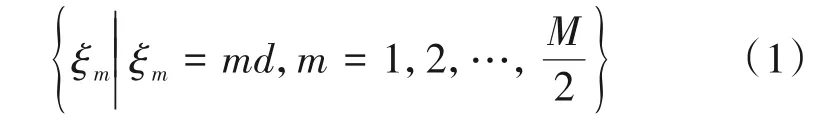
空心点表示第2级子阵，阵元间距为（M/2+1）d，包含M/2个阵元，其阵元位置为：

第m个阵元在第n个快拍的接收信号为：

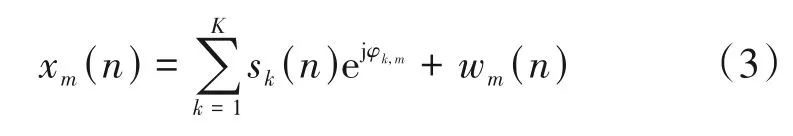
其中m=1，2，…，M，n=1，2，…，N，M表示阵元数，N表示快拍数，sk(n)表示第k个混合源发射信号，wm(n)高斯白噪声，φk，m表示第k个混合源在m个阵元相对于第1 个阵元的时延。对于近场源，φk，m表示为：

其中k=1，2，…，K1，K1表示近场源的个数，rk，m表示第k个近场源与第m个阵元的距离，rk表示第k个近场源的距离，λ表示载波的波长。将rk，m在d/rk进行二阶泰勒展开，近场源的接收信号可以近似表示为：

其中ηk=-2π sinθk/λ，ϕk=π cos2θk/λrk。对于远场源，φk，m表示为：

其中k=1，2，…，K2，K2表示远场源的个数，远场源的接收信号表示为：

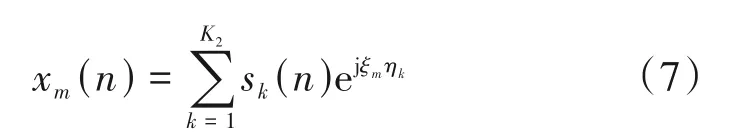
将式（5）和式（7）代入（3），混合源接收信号为：

3 近场源定位方法

由于近场源协方差矩阵符合Hermitian 矩阵形式，远场源协方差矩阵符合Hermitian 和Toeplitz 矩阵形式，本节将混合源协方差矩阵进行差分得到近场源差分向量，利用近场源深度展开ISTA网络得到近场源空间谱，通过空间谱的峰值可以实现近场源的DOA和距离估计。

3.1 近场源差分向量

嵌套阵列下近场和远场混合源接收数据协方差矩阵可以表示为：

其中(·)T表示转置运算，J表示反对角单位矩阵。由式（9）和式（12），近场源差分矩阵可以表示为：

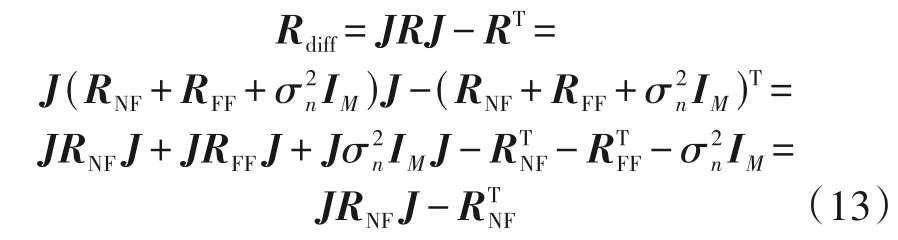
由于近场源协方差矩阵具有以下性质：

因此，差分矩阵中只包含近场源信息，式（13）可以表示为：

将近场源差分矩阵向量化，得到近场源差分向量：

k=1，2，…，K1，⊙表示Khatri-Rao 积，⊗表示Kronecker 积。可以看出，嵌套阵列经过Kronecker 积可以形成虚拟阵元，形成更大的阵列孔径，进而可以提高参数估计精度。

此外，差分向量ydiff的过完备形式可以表示为：

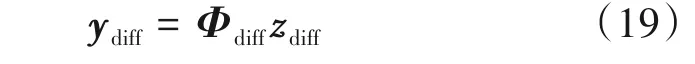
其中分块冗余字典Φdiff可以表示为：

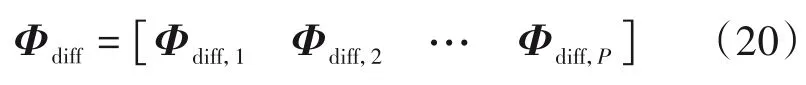
第p块可以表示为：

zdiff表示PQ维向量，当(θp，rq)对应近 场源位 置(θk，rk)时，zdiff的第（p-1）×Q+q个元素为1，其余元素为0。将差分向量的实部和虚部重构为：

其中ℜ(·)表示取实部运算，ℑ(·)表示取虚部运算，由于zdiff的元素为实数，因此上式可以表示为：

3.2 近场源深度展开ISTA网络

近场源深度展开ISTA 网络的结构如图2 所示，网络的层数为L，该网络是将ISTA 算法的迭代步骤级联为神经网络层，其中网络的初始化参数为ISTA算法的参数。

图2 近场源深度展开ISTA网络结构示意图Fig.2 Deep unfolded ISTA network for near-field sources

将diff输入深度展开网络，通过网络的输出可以得到近场源的空间谱。对近场源空间谱进行谱峰搜索，由谱峰所对应的位置即可确定近场源的DOA 估计值和距离估计值，k=1，2，…，K1。近场源深度展开ISTA网络第1层的输出为：

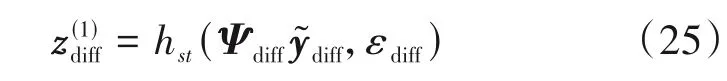
第l层的输出为：

其中l=2，3，…，L，Ψdiff表示PQ×2M2维矩阵，Πdiff表示PQ×PQ维矩阵，εdiff表示近场源软门限函数的阈值，hst(·，ε)表示软门限函数：

其中β表示软门限函数的输入向量，sgn(·)表示符号函数，*表示Hadamard 积，|·|表示绝对值，ε表示阈值。近场源深度展开ISTA 网络的初始化参数如下：

其中αdiff=0.9/δdiff，δdiff表示的最大特征值，IPQ表示PQ维单位矩阵。

在训练近场源深度展开ISTA网络过程中，使用随机梯度下降（Stochastic gradient descent，SGD）优化器对网络参数Ψdiff、Πdiff和εdiff进行更新，损失函数为：

其中t=1，2，…，T，T表示训练样本个数，μdiff表示正则化参数表示2-范数的平方，‖ · ‖1表示1-范数。可以看出损失函数与重构误差和稀疏度有关，在训练过程中不需要使用标签。

4 远场源定位方法

在近场源DOA 和距离参数估计的基础上，本节通过子空间差分得到远场源协方差向量，利用远场源深度展开ISTA网络得到远场源空间谱，通过空间谱的峰值可以实现远场源的DOA估计。

4.1 远场源协方差向量

由混合源M-(K1+K2)个小特征值Δ可以计算得到混合源的噪声功率估计值：

此外，第k个近场源功率的估计值可以表示为：

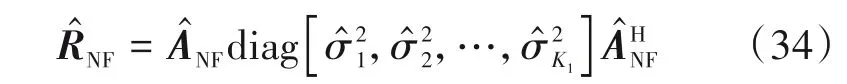
将远场源协方差矩阵的估计值向量化得到远场源协方差向量：

远场源协方差向量的过完备形式可以表示为：

其中冗余字典ΦFF可以表示为：

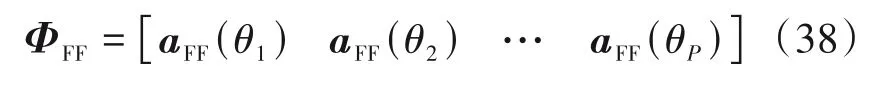
zFF表示P× 1 维向量，当θp对应远场源的DOA 时，zFF的第p个元素为1，其余元素为0。将远场源协方差向量的实部和虚部重构为：

4.2 远场源深度展开ISTA网络

远场源深度展开ISTA 网络的结构如图3 所示，网络的层数为L，将输入深度展开网络，通过网络的输出可以得到远场源的空间谱。对远场源空间谱进行谱峰搜索，由谱峰所对应的位置即可确定远场源的DOA估计值，k=1，2，…，K2。

图3 远场源深度展开网络结构示意图Fig.3 Deep unfolded ISTA network for far-field sources

远场源深度展开ISTA网络第1层的输出为：

第l层的输出为：

其中l=2，3，…，L，ΨFF表示P×2M2维矩阵，ΠFF表示P×P维矩阵，εFF表示远场源软门限函数的阈值，远场源深度展开ISTA网络的初始化参数如下：

其中αFF=0.9/δFF，δFF表示的最大特征值，IP表示P维单位矩阵。

在远场源深度展开ISTA 网络训练过程中使用SGD 优化器对网络参数ΨFF、ΠFF和εFF进行更新，损失函数定义为：

其中t=1，2，…，T，T表示训练样本个数，μFF表示正则化参数。可以看出损失函数与重构误差和稀疏度有关，在训练过程中不需要使用标签。

混合源定位网络如图4 所示，利用协方差矩阵差分方法和子空间差分方法从混合源接收信号中分离出近场源差分向量和远场源协方差向量，通过近场源深度展开ISTA 网络和远场源深度展开ISTA 网络分别对近场源定位和远场源定位。在使用网络对混合源定位之前，需要构建近场源深度展开ISTA 网络和远场源深度展开ISTA 网络，并对其进行训练。在网络训练完成后，通过将混合源协方差矩阵R进行差分得到近场源差分向量，将其输入至近场源深度展开ISTA网络，网络的输出为近场源空间谱，通过空间谱的峰值可以实现近场源的DOA 和距离估计。此外，利用近场源的DOA和距离估计值，通过子空间差分得到远场源协方差向量，将其输入至远场源深度展开ISTA 网络，网络的输出为远场源空间谱，通过空间谱的峰值可以实现远场源的DOA估计。

图4 混合源定位网络Fig.4 Network of mixed source localization

混合源定位流程如图5 所示，利用混合源接收信号得到混合源协方差矩阵，通过协方差矩阵差分得到近场源差分向量，将其输入至近场源深度展开ISTA 网络，得到近场源空间谱，通过空间谱的峰值对近场源的DOA 和距离进行估计。此外，通过对混合源协方差矩阵进行特征值分解，得到混合源特征值和信号子空间，通过子空间差分得到远场源协方差向量，将其输入至远场源深度展开ISTA 网络，得到远场源空间谱，通过空间谱的峰值对远场源的DOA进行估计。

图5 混合源定位流程图Fig.5 Flow chart of the mixed source localization

5 仿真实验

嵌套阵列的近场区域为［0.62（D3/λ）1/2，2D2/λ］，可以看出近场区域与阵列的孔径D和波长λ有关。在仿真实验中，嵌套阵列的阵元个数M设置为8，阵元间距d设置为0.1 m，则阵列孔径D为（M/2）（M/2+1）d=2 m，混合信源的载频设置为300 MHz，则波长为1 m。因此嵌套阵列的近场区域为［1.8 m，8 m］。

对于近场源深度展开ISTA网络，网络的层数设置为30，以1°和0.1 m为间隔分别对DOA[-60°，60°]和距离［1.8 m，8 m］进行均匀采样产生7623个训练样本，epoch和mini-batch设置为100和32；对于远场源深度展开ISTA 网络，网络的层数设置为30，以1°为间隔对DOA 在[-60°，60°]进行均匀采样产生121个训练样本，epoch和mini-batch设置为50和16。

5.1 混合源定位结果

混合源中包含两个近场源和一个远场源，其中近场源设置为（50°，2 m）和（-30°，3.5 m），远场源的设置为（-30°），可以看出近场源位于阵列的近场区域，图6（a）为利用近场源深度展开ISTA 网络获得的近场源空间谱，图6（b）为利用远场源深度展开ISTA 网络获得的远场源空间谱，可以看出谱峰对应近场源和远场源设定值，表明本文构建的深度展开ISTA网络能够实现混合源进行识别和定位。

图6 混合源空间谱Fig.6 Spatial spectrum of mixed sources

5.2 网络泛化能力

下面以近场源深度展开ISTA网络为例，在验证近场源离格DOA 估计的泛化能力时，近场源的距离设置为2λ，产生3组测试样本集，第1组测试样本集的DOA设置为-59.99°，-58.99°，…，-0.99°，0.01°，1.01°，…，59.01°，第2 组测试样本集的DOA 设置为-59.90°，-58.90°，…，-0.90°，0.10°，1.10°，…，59.10°，第3 组测试样本集的DOA 设置为-59.70°，-58.70°，…，-0.70°，0.30°，1.30°，…，59.30°，共计360 个测试样本。在验证近场源离格距离估计的泛化能力时，近场源的DOA 设置为30°，产生2 组测试样本集，第1 组测试样本集的距离设置为1.81 m，1.91 m，…，8.01 m，第2 组测试样本集的距离设置为1.83 m，1.93 m，…，8.03 m，共计126 个测试样本。图7（a）和7（b）分别为近场源DOA 和距离估计结果，图8（a）和8（b）分别为近场源DOA 和距离估计误差，可以看出网络能够将离网DOA 和距离估计到相邻的网格中，表明对DOA 和距离估计具有泛化能力。

图7 近场源估计结果Fig.7 Estimates of near-field sources

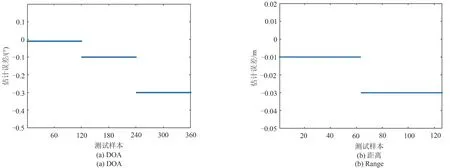
图8 近场源估计误差Fig.8 Errors of near-field sources

5.3 网络收敛速度

为验证本文提出方法的收敛速度，将本文提出在不同层数的深度展开ISTA 网络和在不同迭代次数的模型驱动ISTA 算法的归一化均方根误差（Normalized Mean Squared Error，NMSE）进行了对比。图9（a）和9（b）分别为近场源和远场源的NMSE，其中横坐标表示深度展开ISTA 网络层数或者模型驱动ISTA 算法的迭代次数，纵坐标表示NMSE，加“○”的实线表示深度展开ISTA 网络的NMSE，加“◇”的虚线表示模型驱动ISTA 算法的NMSE。可以看出随着网络层数/迭代次数增加，本文提出的方法和ISTA 算法NMSE 逐渐减小，在相同的网络层数或迭代次数下，本文提出的深度展开ISTA网络比模型驱动ISTA算法收敛速度更快。

图9 深度展开ISTA网络和模型驱动ISTA算法的NMSEFig.9 NMSE of deep unfolded ISTA network and model-based ISTA method

5.4 参数估计RMSE

为验证本文提出方法的参数估计精度，将本文提出的深度展开ISTA 网络的均方根误差（Root Mean Squared Error，RMSE）与文献［10］的空间平滑算法、文献［11］的卷积神经网络方法、模型驱动ISTA 算法和克拉美罗界（Cramér-Rao Bound，CRB）进行了对比。仿真实验中，近场源的位置设置为（50.1°，2.01 m），远场源的DOA 设置为（30.1°），图10（a）、10（b）和10（c）分别为在不同信噪比下，经过300 次蒙特卡洛实验得到的近场源DOA、近场源距离和远场源DOA 的RMSE。可以看出，随着信噪比的增加，三种方法的RMSE 逐渐减小，表明参数估计精度逐渐提高。在相同的信噪比下，相较于其他方法，本文提出的深度展开ISTA 网络的RMSE 更低，更加接近CRB 曲线，参数估计精度更高。

图10 混合源参数估计RMSEFig.10 RMSE of parameter estimation for mixed sources

6 结论

本文通过混合源协方差矩阵差分方法和子空间差分方法分别得到近场源差分向量和远场源协方差向量，利用近场源深度展开ISTA网络和远场源深度展开ISTA 网络分别得到近场源空间谱和远场源空间谱。最后利用远场源深度展开ISTA 网络得到远场源空间谱。仿真实验表明本文提出的网络能够实现混合源识别和定位，相较于模型驱动ISTA算法，经过训练的深度展开ISTA网络的收敛速度更快，定位精度更高。