基于矩阵差分的远场和近场混合源定位方法

刘振 苏晓龙 刘天鹏 彭 勃 陈 鑫 刘永祥

(国防科技大学电子科学学院 长沙 410073)

1 引言

混合源定位在无源雷达中具有广泛的应用前景[1,2]。按照空间中的辐射源与阵列之间的相对距离，可以将辐射源分为远场源和近场源。对远场源定位，需要对波达方向(Direction Of Arrival,DOA)进行估计；对近场源定位，除了对波达方向进行估计，还需要对距离参数进行估计。阵列的近场区域小于2D2/λ，其中D为圆阵孔径，λ为波长[3,4]。虽然远场源可以视为距离为无穷远的近场源，但是当远场源的二维DOA与近场源二维DOA相同时，如果采用近场和远场参数联合估计将无法对混合源进行识别。此外，由于远场源定位场景和近场源定位场景可以看作混合源定位场景特殊模式，因此混合源定位方法同样适用于辐射源全部为远场源定位场景或者辐射源全部为近场源定位场景。

不同于单独对远场源进行定位的方法和单独对近场源进行定位的方法，对混合源进行定位还需要对近场源和远场源进行分类和识别。文献[5]首先利用距离为无穷远时的近场源导向矢量和混合源的噪声子空间，通过一维多重信号分类(One Dimensional MUltiple SIgnal Classification,1-D MUSIC)方法估计出远场源DOA，接着利用对称阵元的2阶统计量去除近场源的距离参数，估计出混合源DOA并通过斜投影算法对混合源进行分类，最后将近场源DOA代入后导向矢量和混合源噪声子空间，通过1-D MUSIC方法对近场源距离进行估计。文献[6]提出了基于子空间的混合源定位算法，该算法利用线性变换估计出远场源的DOA，通过正交三角分解(QR分解)得到斜投影算子避免了特征值分解，大大减少了计算复杂度，利用1-D MUSIC方法确定近场源DOA，最后将近场源DOA代入导向矢量，确定近场源的距离参数。该方法有效解决了在快拍数有限时出现饱和的情况。文献[7]利用两级对称嵌套线阵，利用距离为无穷远的近场源导向矢量和混合源的噪声子空间，通过1-D MUSIC方法估计出远场源DOA，接着利用斜投影方法去除混合源接收信号中的远场分量，计算近场源在对称阵元下的4阶累积量并进行向量化处理，估计出近场源DOA，最后利用代入近场源DOA的导向矢量和混合源噪声子空间，确定近场源的距离参数。该方法能够在阵元数相同的情况下增大阵列孔径，提高混合源参数估计精度。上述3种方法在得到远场源的波达方向的基础上，利用斜投影算法将远场源和近场源进行分离，但是在远场源参数估计的基础上利用斜投影算法得到的近场源分量会受到噪声分量的影响，引起近场源参数估计误差，导致定位精度下降。文献[8]利用协方差矩阵差分方法消除混合源中远场源和噪声分量，得到近场源差分矩阵，该方法能够有效避免噪声分量对近场源定位精度的影响，文献[9]采用降秩的方法从混合源中分离出远场源分量，文献[10]设计了3个4阶累积量矩阵消除近场源导向矢量中距离参数，进而同时估计出远场源和近场源的波达方向。但是上述方法采用线阵对混合源进行定位只能估计出一维波达方向，并且线阵在0°波达方向的分辨率最高，在60°波达方向的分辨率会降低1/2。

相较于均匀线阵只能对一维波达方向进行估计，均匀圆阵可以实现方位角和俯仰角等二维波达方向估计[11–13]，并且在不同方位角的分辨率具有各向同性[14,15]。在现有文献中，由于均匀圆阵的导向矩阵不具有均匀线阵导向矩阵的Vandermonde形式，不便于在数学上进行处理，因此提出的方法相对较少。均匀圆阵下对混合源进行定位需要针对相应的数学模型进行分析，文献[16]采用均匀圆阵，提出了TSMUSIC方法，该方法利用均匀圆阵下的远场源的协方差矩阵具有Hermitian和Toeplitz形式，而近场源的协方差矩阵只具有Hermitian形式，利用传播算子的正交性得到近场源的噪声子空间，进而通过2-D MUSIC方法得到近场源二维DOA的空间谱，进而根据谱峰确定近场源二维DOA；接着，利用将近场源二维DOA代入后的导向矢量和混合源的噪声子空间，通过1-D MUSIC方法确定近场源的距离；最后，利用远场源的导向矢量和混合源的噪声子空间确定远场源的二维DOA。该方法参数估计精度较高，但是计算复杂度较大。文献[17]采用均匀圆阵，利用每个阵元的频谱计算非相干的混合源在每个阵元的相位，利用均匀圆阵中心对称的特点，通过计算对角阵元的相位差来去除近场源的距离参数，得到混合源二维DOA的相位差矩阵，进而运用最小二乘法同时估计出远场源和近场源的方位角与俯仰角；接着，根据1-D MUSIC方法得到距离空间谱的收敛性，对混合源进行识别并估计出近场源的距离参数，当距离空间谱出现峰值，该混合源判断为近场源，峰值所对应的位置即为近场源的距离；若距离空间谱不收敛，则该混合源判断为远场源。基于相位差的方法能够有效减少计算复杂度，但是混合源的定位精度有所降低。

针对上述方法存在的问题，本文根据均匀圆阵中心对称的特点，提出一种基于协方差矩阵差分的混合源定位方法，该方法首先利用二维多重信号分类方法估计出远场源的方位角和俯仰角；接着利用协方差矩阵差分方法提取出近场源差分矩阵，通过改进类旋转不变估计信号参数(Estimation of Signal Parameters via Rotational Invariance Techniques like,ESPRIT-like)方法计算出近场源的方位角和俯仰角；最后，利用一维多重信号分类方法估计出近场源的距离。该方法能够消除混合源协方差矩阵中的远场源的噪声分量，从而提取出近场源差分矩阵，并且相较于基于相位差的方法，本文提出的方法能够提高混合源的定位精度。当远场源的二维DOA与近场源二维DOA相同时，如果采用近场和远场参数联合估计将无法对混合源进行识别，采用本文所提的两步法可以将远场源和近场源进行有效分离，在混合源识别上更具优势。

2 混合源模型

均匀圆阵下的混合源模型如图1所示，以均匀圆阵的圆心为原点建立三维坐标系，均匀圆阵的半径为R，由分布在xy平面上的M个阵元组成，混合源包含K1个远场源和K2个近场源，方位角参数ϕ为混合源与均匀圆阵中心的连线投影到xy平面上，相对于x坐标轴的逆时针方向旋转的角度；俯仰角参数θ为混合源与均匀圆阵中心的连线相对于z坐标轴旋转的角度；当混合源为近场源时，距离参数r为近场源与均匀圆阵中心的距离。

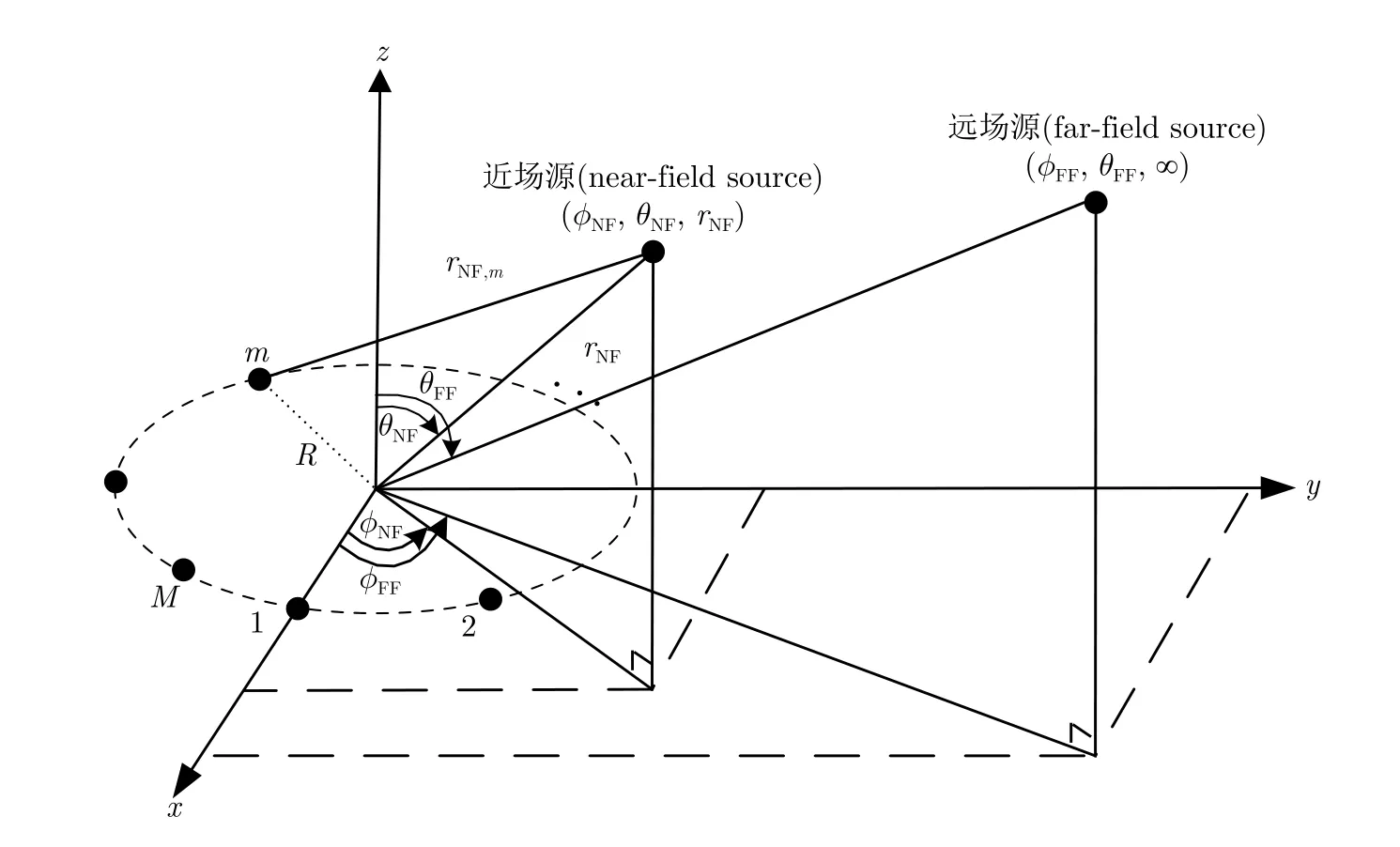
图1 混合源模型Fig.1 The geometric model of mixed sources

均匀圆阵的第m个阵元在第n个快拍的接收数据可以表示为

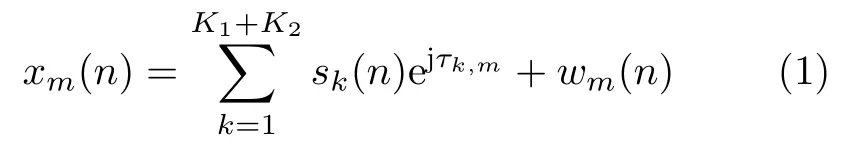
其中，sk(n)表示第k个混合源发射数据，wm(n)表示零均值复白高斯过程，τk,m表示第k个混合源到达阵列中心以及到达第m个阵元的时差，当混合源为远场源时，时差可以表示为

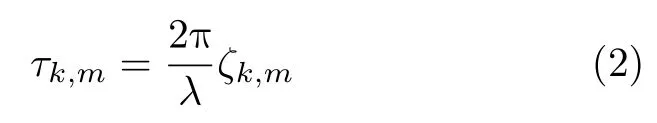
其中，k=1,2,···,K1，λ表示波长，2π/λ表示波数，ζk,m=cos(φm −ϕk)sinθk,φm=2π(m −1)/M，当混合源为近场源时，时差可以表示为

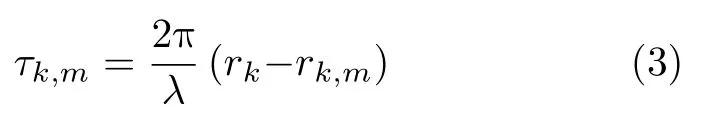
其中，k=K1+1,K1+2,···,K1+K2,rk,m表示第k个近场源与第m个阵元的距离，rk,m通过2阶泰勒级数[11]可以展开为

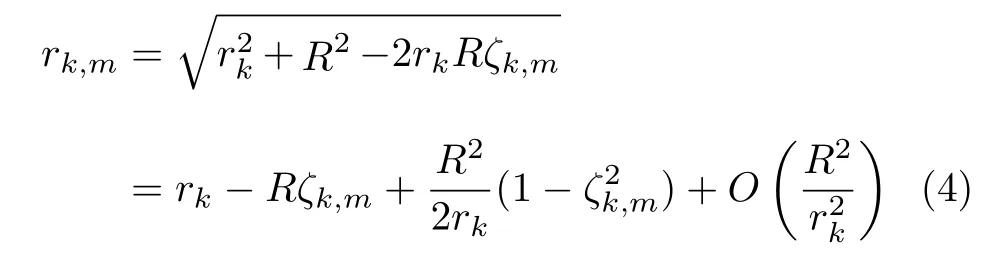
将式(2)和式(4)代入式(1)，混合源模型可以简化为

3 算法描述

在均匀圆阵下的近场和远场混合源数学模型的基础上，本节首先利用2-D MUSIC方法估计出远场源的方位角和俯仰角，实现远场源定位；接着利用协方差矩阵差分方法提取出近场源差分矩阵，进而通过改进的类旋转不变估计信号参数方法计算出近场源的方位角和俯仰角；最后利用1-D MUSIC方法估计出近场源的距离，实现近场源定位。

3.1 远场源二维DOA参数估计

均匀圆阵下混合源的协方差矩阵E可以由式(6)计算

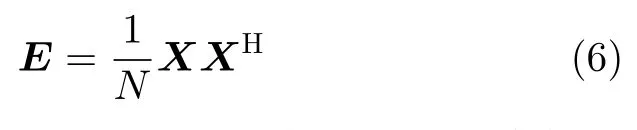
其中，X=[x(1)x(2)··· x(N)]表示M ×N维的混合源接收数据，x(n)=[x1(n)x2(n)··· xM(n)]T表示第n个快拍接收数据，(·)H表示共轭转置，N为混合源的快拍数，(·)T表示转置运算。

对混合源的协方差矩阵E进行特征值分解得到

利用3-D MUSIC方法得到混合源的空间谱函数

其中，aNF(ϕ,θ,∞)=[aNF,1(ϕ,θ,∞)aNF,2(ϕ,θ,∞)···aNF,M(ϕ,θ,∞)]T表示距离为无穷远情况下的近场源导向矢量，即远场源导向矢量，此时aNF,m(ϕ,θ,∞)=ej(2πR/λ)ζm(ϕ,θ),m=1,2,···,M。只包含方位角和俯仰角等二维DOA。对远场源方位角和俯仰角的空间谱函数VFF(ϕ,θ)进行谱峰搜索，峰值所对应的位置即为远场源的方位角估计值和俯仰角估计值，则第k个远场源的定位结果为k=1,2,···,K1。

3.2 混合源协方差矩阵差分

混合源协方差矩阵E可以表示为

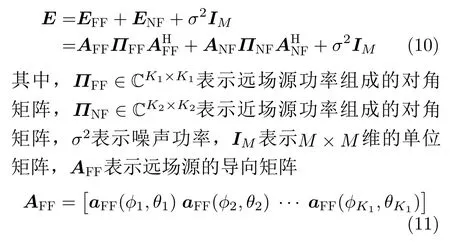
由于均匀圆阵具有中心对称的结构，满足φm+M/2=φm+π和ζm+M/2=−ζm，因此，远场源的导向矢量可以表示为

同理，ANF表示近场源的导向矩阵为

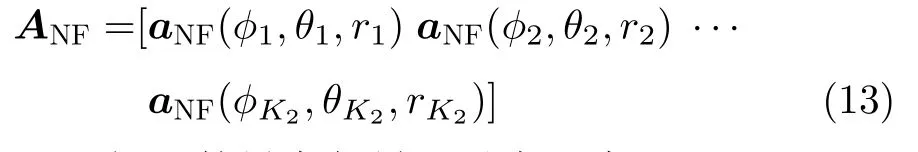
其中，近场源的导向矢量可以表示为

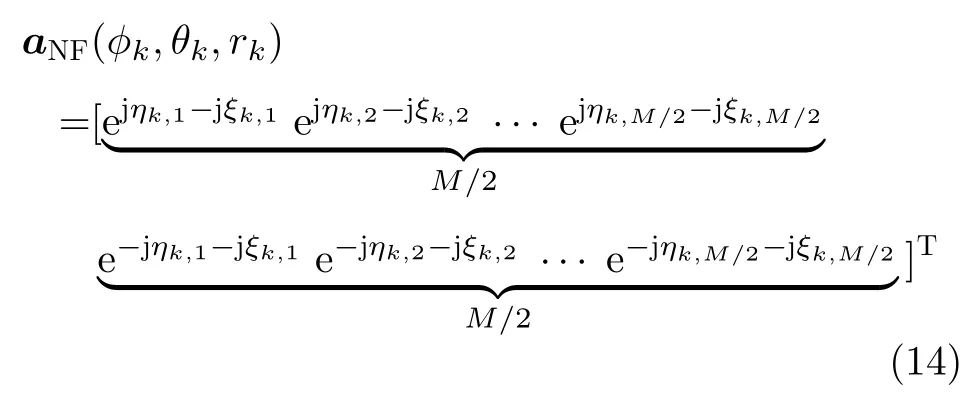
由于远场源的导向矢量中第m个元素和第m+M/2个元素具有共轭的结构，因此远场源的协方差矩阵EFF可以表示为

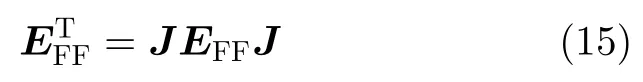
其中，旋转变换矩阵J可以表示为

OM/2和IM/2分别为M/2×M/2维的零矩阵和单位矩阵。

由式(10)和式(15)可以推导近场源差分矩阵为

其中，近场源差分矩阵的导向矩阵可以表示为

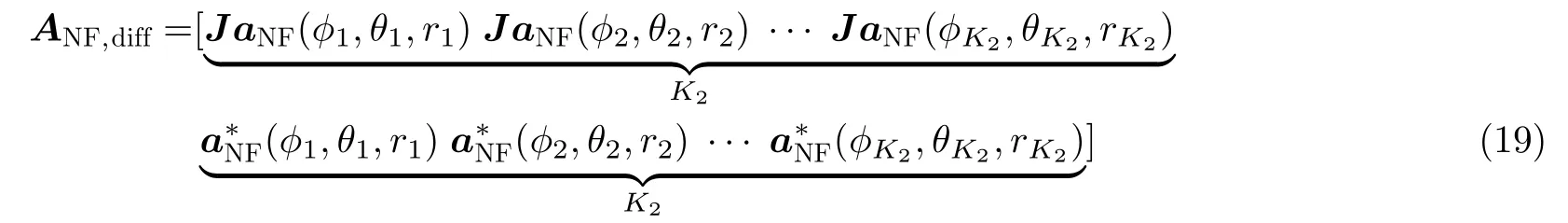
其中，第k个导向矢量可以表示为

第k+K2个导向矢量可以表示为

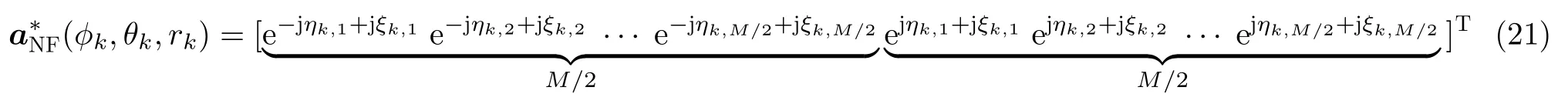
由于ANF,diff的第k列的指数项第1部分与第k+K1列的指数项第1部分相同，各列中第m个元素的指数项第2部分与第m+M/2个元素的指数项第2部分相同，因此可以得到

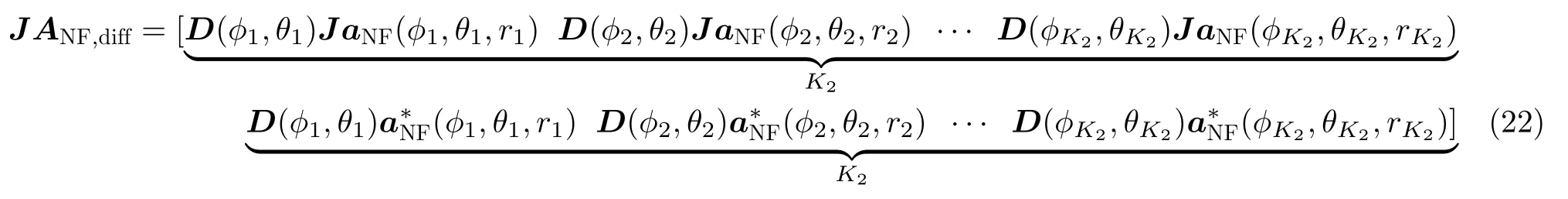
其中，D(ϕk,θk)表示为

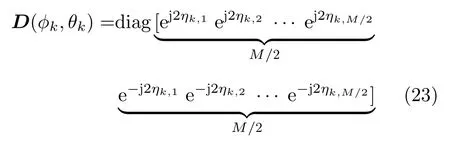
D(ϕk,θk)只包含近场源的二维DOA参数，因此可以利用D(ϕk,θk)将近场源三维位置参数估计分解为二维DOA估计和距离参数估计，能够有效降低计算复杂度。

3.3 近场源二维DOA参数估计

对仅包含近场源差分矩阵ENF,diff进行特征值分解

存在一个满秩矩阵G使得

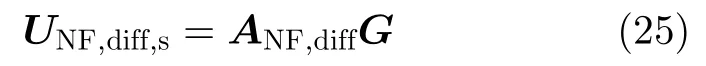
由式(22)和式(19)可以得到

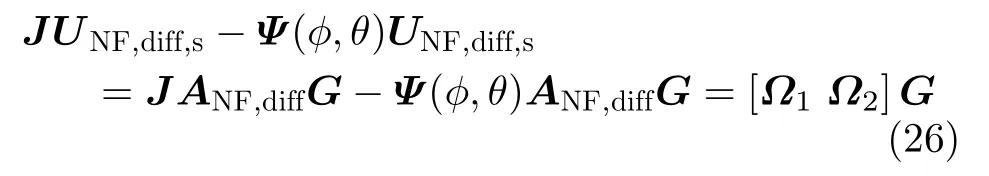
其中，

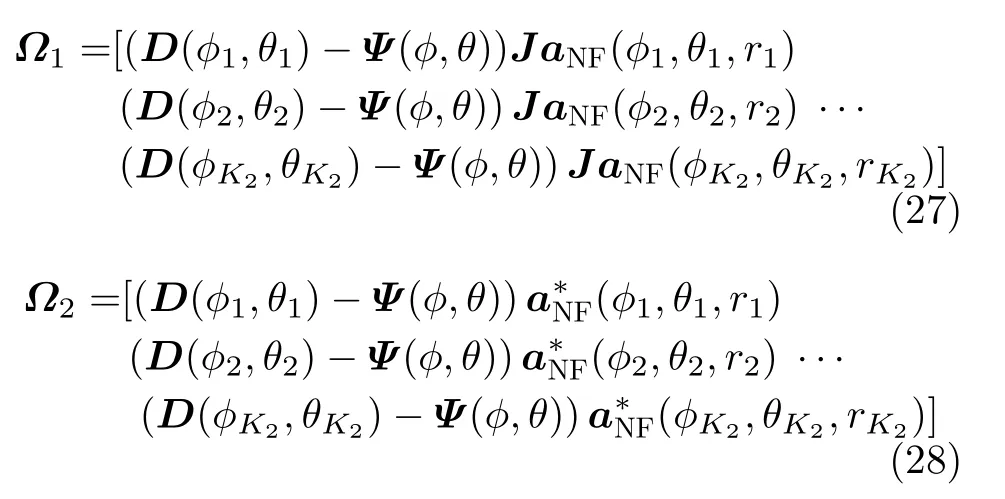
当D(ϕk,θk)=Ψ(ϕ,θ)时，JUNF,diff,s−Ψ(ϕ,θ)UNF,diff,s=0。因此，可以通过改进的ESPRITlike方法[15]得到近场源二维DOA的空间谱函数

其中，det(·)表示行列式的值，Q为M ×2K2维随机满秩矩阵，J为3.2节确定的M ×M维旋转变换矩阵，对角矩阵Ψ(ϕ,θ)为

diag(·)表示将向量转化为对角矩阵运算。对近场源方位角和俯仰角的空间谱函数VNF(ϕ,θ)进行谱峰搜索，峰值所对应的位置即为近场源的方位角估计值和俯仰角估计值,k=1,2,···,K2。

3.4 近场源距离参数估计

在估计出近场源的方位角和俯仰角的基础上，通过1-D MUSIC方法得到第k个近场源的距离空间谱函数

4 算法分析

4.1 计算复杂度分析

对于均匀圆阵下的近场源定位，传统的3-D MUSIC方法通过三维谱峰搜索估计出近场源方位角、俯仰角和距离，本文首先通过改进的ESPRITlike方法得到近场源的二维DOA空间谱，利用二维谱峰搜索估计出近场源的方位角和俯仰角，进而利用1-D MUSIC方法得到近场源的距离空间谱，利用一维谱峰搜索估计出近场源的距离。本文提出的方法需要M2N次乘法和M2(N −1)次加法计算混合源协方差矩阵，需要2M2N次乘法和M2次减法计算近场源差分矩阵，需要O(M2)量级的计算复杂度分别对混合源协方差矩阵以及近场源差分矩阵进行特征值分解，需要O(M2)量级的计算复杂度得到远场源二维DOA 空间谱，需要次乘法、次加法和次减法得到近场源二维DOA空间谱，需要O(M)量级的计算复杂度得到近场源距离空间谱。

4.2 混合源能量差异敏感性分析

由于本文所提的两步法通过协方差矩阵差分去除混合源的远场源和噪声分量，进而提取出近场源差分矩阵，因此对近场源进行估计时不受远场源和噪声能量的影响。本文第1步在对远场源进行估计时，当远场源的能量远远小于近场源的能量，此时通过第1步的方法对远场源进行定位的性能急剧恶化。为了解决两个源能量差异敏感的问题，可以首先对噪声能量进行估计，去除混合源协方差矩阵中的噪声分量；利用第2步的近场源估计结果，通过斜投影算法去除无噪混合源协方差矩阵中近场源分量，进而得到远场源分量。具体步骤如下：

混合源的协方差矩阵可以分解为

噪声的能量可以通过式(33)计算

并可以通过式(36)计算

进而远场源的协方差矩阵可以通过式(38)计算

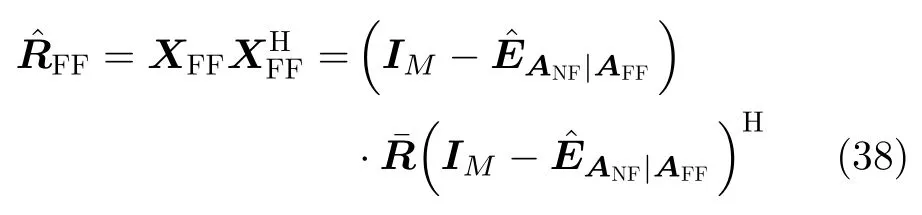
此时，可以减少两个源的能量差异对远场源二维DOA估计的影响。

4.3 算法总结

基于协方差矩阵差分的混合源定位方法流程图如图2所示，对于远场源定位，本文利用均匀圆阵下的混合源接收数据得到混合源协方差矩阵，利用远场源导向矢量以及经过特征值分解得到的混合源噪声子空间，通过2-D MUSIC方法估计出远场源的方位角和俯仰角；对于近场源定位，本文利用混合源协方差矩阵和旋转矩阵得到近场源差分矩阵，利用随机满秩矩阵、对角矩阵以及经过特征值分解的近场源信号子空间，通过改进的ESPRIT-like方法计算出近场源的方位角和俯仰角，利用近场源的导向矢量和混合源的噪声子空间，通过1-D MUSIC方法估计出近场源的距离。本文根据均匀圆阵下的远场源在中心对称阵元的导向参数具有共轭性质，利用协方差矩阵差分方法去除混合源的远场源分量，得到近场源差分矩阵。由于协方差矩阵差分方法没有利用第1步的远场源二维DOA参数估计结果，因此，第2步近场源参数估计性能与远场源DOA估计性能无关。或者说，第1步和第2步的顺序也可以进行互换，可以先通过混合源协方差矩阵差分方法得到近场源差分矩阵，估计出近场源位置参数，再利用2-D MUSIC方法估计远场源DOA参数。另外，在多个混合源能量相同的场景下，由于第1步利用远场源导向矢量与噪声子空间的正交性，因此不会将近场源判断为远场源。当近场源的距离临近2D2/λ，由于噪声和模型误差的影响，第1步可能会将近场源的方向判断为远场源。当远场源的二维DOA与近场源二维DOA相同时，如果采用近场和远场参数联合估计将无法对混合源进行识别，采用本文所提的两步法可以将远场源和近场源进行有效分离，在混合源识别上更具优势。

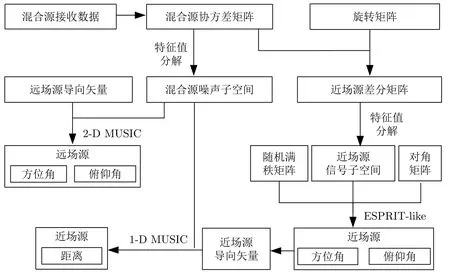
图2 基于协方差矩阵差分的混合源定位方法流程图Fig.2 Flow chart of the mixed source localization based on the covariance differencing method

5 仿真实验

本节通过MATLAB仿真验证提出方法对混合源的定位效果，仿真中均匀圆阵的阵元个数为8，半径为0.5m，以均匀圆阵的中心为原点建立三维坐标系，混合源包含一个远场源和一个近场源，远场源的位置为(50°,30°,∞)，近场源的位置为(55°,35°,10m)。

5.1 混合源定位有效性

这一小节用于验证本文提出方法得到的空间谱对远场和近场混合源的定位效果，在信噪比为20dB，快拍数为600时，图3为通过本文提出方法得到的混合源定位的空间谱，图3(a)为通过2-D MUSIC方法得到的远场源二维DOA空间谱，方位角估计范围为0.1°～360°，间隔为0.1°，俯仰角估计范围为0°～90°，间隔0.1°，可以看出二维空间谱中出现的一个峰值对应的位置为(50.0°,30.2°)，即为远场源方位角和俯仰角估计。图3(b)为通过改进的ESPRIT-like方法得到的近场源二维DOA空间谱，同样地，方位角估计范围为0.1°～360°，间隔为0.1°，俯仰角估计范围为0°～90°，间隔0.1°，可以看出二维空间谱中出现的一个峰值对应的位置为(55.0°,35.1°)，即为近场源方位角和俯仰角估计。图3(c)为通过1-D MUSIC方法得到的近场源一维距离空间谱，近场源距离估计范围为0.1～30.0m，间隔为0.1m，图中红色的线表示近场源真实距离，可以看出距离空间谱中出现的一个峰值对应的位置为9.9m，即为近场源距离估计。综上可知，本文所提协方差矩阵差分方法能够从混合源中提取出近场源分量，并通过改进的ESPRIT-like方法近场源三维位置参数中分离出二维DOA，最终实现混合源的有效定位。

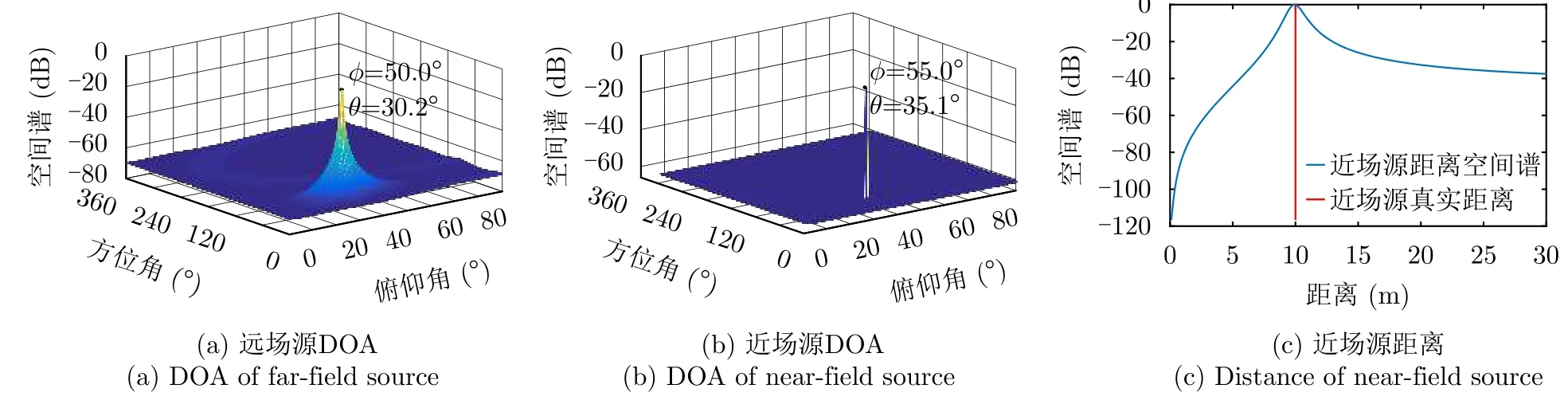
图3 混合源空间谱Fig.3 Spatial spectrum of mixed sources

5.2 不同信噪比下混合源定位精度

本节验证所提方法在不同信噪比下对混合源的定位性能，并与TSMUSIC方法[16]、相位差方法[17]以及克拉美罗界(Cramer-Rao Lower Bound,CRLB)进行对比，其中TSMUSIC方法是利用2-D MUSIC方法分别估计出远场源和近场源的二维DOA，利用1-D MUSIC方法分别估计出近场源的距离；相位差方法是利用均匀圆阵下对角阵元的相位差，通过最小二乘法同时估计出远场源和近场源的二维DOA，根据1-D MUSIC方法对混合源进行识别并估计出近场源的距离参数；CRLB是参数任意无偏估计量的下限。在仿真中利用均方根误差(Root Mean Square Error，RMSE)对算法的性能进行分析，RMSE可由式(39)计算

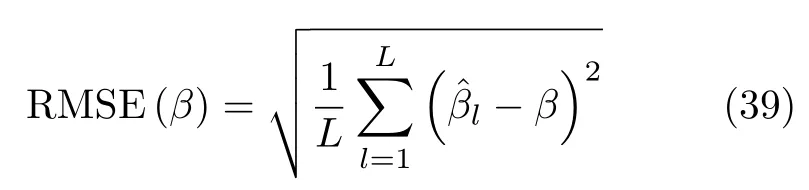
其中，L表示独立重复仿真次数，表示第l次的混合源参数估计结果，l=1,2,···,L,β表示混合源的真实位置参数。当快拍数为600时，图4(a)—图4(e)分别为通过600次独立重复仿真得到在不同信噪比下的远场源方位角RMSE、远场源俯仰角RMSE、近场源方位角RMSE、近场源俯仰角RMSE以及近场源距离RMSE，从图4可以看出混合源的RMSE随着信噪比的增大而降低，表明混合源参数估计精度不断提高。另外，还可以看出本文所提基于协方差矩阵差分方法的混合源定位精度比基于相位差方法的定位精度高。由于本文方法与TSMUSIC方法都采用2-D MUSIC方法对远场源进行定位，因此两种方法的远场源定位精度相当，本文所提改进ESPRIT-like方法对近场源二维DOA参数估计精度略低于TSMUSIC方法参数估计精度。此外，由于近场源距离估计是在近场源二维DOA估计基础上进行的，相较于近场源二维DOA估计误差，近场源距离估计误差相对较大，从图4中也可以看出，在信噪比为20dB时，近场源的二维DOA估计误差接近0.01°，而近场源的距离误差接近于0.1m。

图4 不同信噪比下混合源RMSEFig.4 RMSE of mixed sources versus SNR

5.3 不同快拍数下混合源定位精度

本节进一步验证在不同快拍数下混合源的定位性能，本文所提方法同样与TSMUSIC方法、相位差方法以及克拉美罗界进行了对比。当信噪比为20dB时，图5(a)—图5(e)分别为通过600次独立重复仿真得到在不同快拍数下的远场源方位角RMSE、远场源俯仰角RMSE、近场源方位角RMSE、近场源俯仰角RMSE以及近场源距离RMSE，从图5中可以看出混合源RMSE随着快拍数的增大而降低，表明混合源参数估计精度逐渐提高。另外，从图中可以看出当快拍数小于600时，混合源RMSE快速下降，当快拍数超过600时，混合源RMSE逐渐平缓。此外，从图5可以看出本文提出方法的混合源定位精度比基于相位差方法的定位精度高，对于远场源参数估计精度，本文提出的方法与TSMUSIC方法相当，对于近场源参数估计精度，本文提出的方法略低于TSMUSIC方法。

5.4 混合源能量差异性对比

由于本文所提的两步法通过协方差矩阵差分去除混合源的远场源和噪声分量，进而提取出近场源差分矩阵，因此对近场源进行估计时不受远场源和噪声能量的影响。图6(a)—图6(c)给出了当近场源和远场源能量比(Near-field and Far-field source Power Ratio,NFPR)分别为1.0,0.2和0.1时的近场源空间谱，可以看出近场源空间谱出现一个峰值，峰值所对应的位置即为近场源二维DOA。仿真结果表明，通过本文提出的算法对近场源进行估计时不受远场源和噪声能量的影响。

依据待检样品标签声称的乳酸菌类别和含量，估算待检样品中是否含有双歧杆菌和乳杆菌及其数量，选择（2～3）个合适的连续稀释度，每个稀释度吸取1 mL样品稀释液置于无菌培养皿内，每个稀释度做两个平行。同时分别吸取1 mL空白稀释液加入两个无菌平皿内作空白对照。然后注入约15mL冷却至（48±1）℃的MRS培养基，转动培养皿使之混合均匀。待培养基凝固后置于（36±1）℃培养箱中厌氧培养（72±2）h，培养后计数与计算。

为了解决远场源对能量差异敏感的问题，通过对信噪比和近场源进行估计，去除混合源协方差矩阵中的噪声分量和近场源分量，得到式(38)远场源协方差矩阵，进而估计远场源二维DOA。图7(a)—图7(c)给出了当近场源和远场源能量比分别为1,5和10时的近场源空间谱，可以看出远场源空间谱出现了一个峰值，峰值所对应的位置即为远场源二维DOA。仿真结果表明，通过本文提出的算法对近场源进行估计时不受远场源和噪声能量的影响。仿真结果表明，所提算法能够有效地解决远场源能量差异敏感的问题。

6 结论

本文所提均匀圆阵下利用混合源协方差矩阵差分的方法能够消除混合源中的近场源和噪声分量，提取出近场源差分矩阵，实现远场源和近场源的有效分离，利用2-D MUSIC方法估计出远场源的方位角和俯仰角，通过改进的ESPRIT-like方法提取并估计出近场源的方位角和俯仰角，运用1-D MUSIC方法估计出近场源的距离参数。仿真结果表明，相较于基于相位差的混合源定位算法，本文所提方法能够提高混合源的定位精度。由于协方差矩阵差分方法没有利用第1步的远场源二维DOA参数估计结果，因此，第2步近场源参数估计性能与远场源DOA估计性能无关。或者说，第1步和第2步的顺序也可以进行互换，可以先通过混合源协方差矩阵差分方法得到近场源差分矩阵，估计出近场源位置参数，再利用2-D MUSIC方法估计远场源DOA参数。另外，在多个混合源能量相同的场景下，由于第1步利用远场源导向矢量与噪声子空间的正交性，因此不会将近场源判断为远场源。当近场源的距离临近2D2/λ，由于噪声和模型误差的影响，第1步可能会将近场源的方向判断为远场源。当远场源的二维DOA与近场源二维DOA相同时，如果采用近场和远场参数联合估计将无法对混合源进行识别，采用本文所提的两步法可以将远场源和近场源进行有效分离，在混合源识别上更具优势。