基于岩石物理的页岩储层各向异性表征

刘　财　邓馨卉　郭智奇*　刘喜武　刘宇巍

(①吉林大学地球探测科学与技术学院，吉林长春 130026； ②页岩油气富集机理与有效开发国家重点实验室，北京 100083；③中国石化页岩油气勘探开发重点实验室，北京 100083； ④中国石化石油勘探开发研究院，北京 100083)

1　引言

由于页岩矿物组分和微观结构复杂，因此页岩储层评价对于地球物理方法和技术的要求很高[1-5]。天然发育的微观孔隙和裂缝是页岩储层中油气储存和运移的通道，对储层评价以及甜点区识别具有重要意义。

页岩的微观物性特征一般表现为宏观VTI性质。黏土矿物的定向排列和水平缝的存在是影响储层VTI特性的主要因素[6-10]。目前，对黏土矿物的研究较多，而针对页岩水平缝的岩石物理研究尚不充分。

前人主要通过分析岩石物理模型正演结果的各向异性特征描述页岩中的裂缝特性。Hudson[11，12]和Schoenberg[13]通过建立等效介质岩石物理模型描述裂缝介质的地震各向异性特征；Schoenberg等[14，15]在长波长条件下，研究了在具有水平缝的各向异性介质中弹性波通过滑动裂缝界面的响应特征，认为裂缝介质的地震响应可以等效为各向同性背景和水平缝引起的各向异性扰动的综合作用结果；Liu等[16]应用地震各向异性理论描述裂缝特征取得了较好效果。

在储层各向异性与地震波传播特征的研究方面，Thomsen[17]提出了弱各向异性理论，并用五个参数表征各向异性的影响； Ruger[18，19]研究了VTI介质的反射特征，并推导了VTI介质反射系数近似方程； Carcione[20]研究了页岩各向异性参数随孔隙压力和干酪根含量的变化规律； Ran等[21]通过重构裂缝储层的弹性参数和各向异性参数，实现了弹性参数和裂缝参数的叠前地震反演。

本文针对罗家地区A井测井数据，应用Backus平均方法[22]将模型从测井尺度粗化至地震尺度，应用各向异性传播矩阵模拟页岩含油储层的地震AVO响应，并结合实际地震资料进行井震标定。之后，基于VTI介质反射系数理论公式[19]进行VTI介质参数AVO反演，并应用井中岩石物理反演结果进一步计算页岩含油储层的裂缝空间分布，反演结果证明了文中方法的有效性。

2　各向异性AVO响应模拟

2.1　Backus平均理论

Backus[22]将层状介质在长波长条件下等效为均匀TI介质。该理论是一种对测井曲线进行尺度粗化的有效理论，同时考虑了层状介质在长波长条件下的各向异性特征[23，24]。因此，在地震数据分析过程中，为了有效进行测井尺度粗化，目前主要采用Backus平均方法，Schoenberg等[14]进一步将其推广到具有任意各向异性的层状介质情况。Kumar[25]将Backus平均理论用于具有低对称各向异性的裂缝型页岩含油储层中。对于VTI介质，由Backus平均理论计算得到地震尺度的等效VTI介质的五个独立的模量

(1)

2.2　各向异性传播矩阵理论

地震尺度的模型可等效为由一系列薄层组成的互层结构，由于干涉、调谐等现象的存在，其反射波呈复合波形。影响薄互层介质地震反射特征的因素有入射角、物性差异、入射波频率、地层厚度、薄互层结构等。Rokhlin等[26]给出了层状介质反射系数表达式。Carcione[27]进一步提出了用于计算薄互层反射系数的广义传播矩阵理论。根据该理论，对于P波入射，在薄互层介质中的反射、透射系数可以表示为

r=[RPP,RPS,TPP,TPS]T

(2)

式中：RPP、RPS、TPP、TPS分别为PP波、PS波的反射、透射系数；A1与A2分别为与上、下层介质物性参数有关的传播矩阵；Bα(α=1,…,N)为具有N层结构的中间薄互层的传播矩阵；iP为P波入射向量。详细公式与计算流程见附录A。

2.3　Ruger理论

基于反射界面两侧的弹性参数的弱不连续性假设，Ruger[19]提出了VTI介质PP波反射系数近似公式

=P+Bsin2θ+Asin2θtan2θ

(3)

(4)

界面两侧弹性参数的弱不连续性和弱各向异性由Thomsen参数

(5)

所表示。式(3)中的弱各向异性VTI介质的Thomsen参数表达式为

(6)

(7)

(8)

(9)

(10)

式中cij为目标介质的弹性刚度系数。

3　水平缝密度叠前地震反演

根据上述VTI介质反射系数理论，本文提出VTI介质各向异性参数反演方法。式(3)的矩阵形式表达为

(11)

则

(12)

式中：P为与声阻抗差异相关的零角度反射系数;B反映了非零角度横波速度的影响；A为近临界角的振幅曲率。

根据Ruger的VTI介质反射系数理论公式，P、B和A分别为

(13)

式中VP01和VP02分别为目标反射界面两侧的P波垂直方向速度。当假设目标层反射界面两侧密度比趋于稳定不变时，P可以近似为

(14)

由

Δε=ε2-ε1≈2(A-P)

(15)

可以得到目标层两侧P波各向异性参数的变化。当下伏岩层为各向同性时，上覆岩层的各向异性参数可表达为

ε1≈2(P-A)

(16)

因此通过计算P和A，可求得目标层页岩的P波各向异性参数，并根据井中岩石物理反演得到的各向异性参数与水平缝密度之间的关系进一步计算页岩水平缝的空间分布。

4　应用实例

4.1　页岩油储层测井数据分析

岩心观测表明，页岩含油储层裂缝系统发育。图1为罗家地区A井页岩含油储层的测井曲线。由图可见： 在约3060m深度处存在弹性性质突变界面，测井解释表明该界面以上为富有机质页岩含油储层，具有高电阻率、低密度(图1c)和低速度(图1b)特征，界面以下为泥质灰岩，具有相对较高的速度和密度以及较低的孔隙度(图1d)； 在新、老地层过渡位置，随深度增加储层岩石中方解石和白云石含量增加，而黏土和石英含量减少(图1e)，导致伽马值逐渐降低。

图1　罗家地区A井页岩含油储层测井数据(a)自然伽马； (b)纵波速度； (c)密度； (d)孔隙度； (e)矿物体积含量

图2为罗家地区A井页岩含油储层的岩心扫描电镜(SEM)与地层微电阻扫描成像(FMI)结果，可观察到页岩在水平背景下水平缝较发育。

4.2　正演模拟及井震标定

图3为罗家地区A井及等效介质测井曲线。将尺度粗化后的数据作为输入模型，应用各向异性传播矩阵理论计算合成地震记录，使用主频为25Hz的雷克子波，目标层对应的时间约为2408ms。图4为正演模拟与井震标定结果，可见目标层位(红线)下方对应正反射系数。

图2　罗家地区A井页岩含油储层的SEM(a)与FMI(b)结果

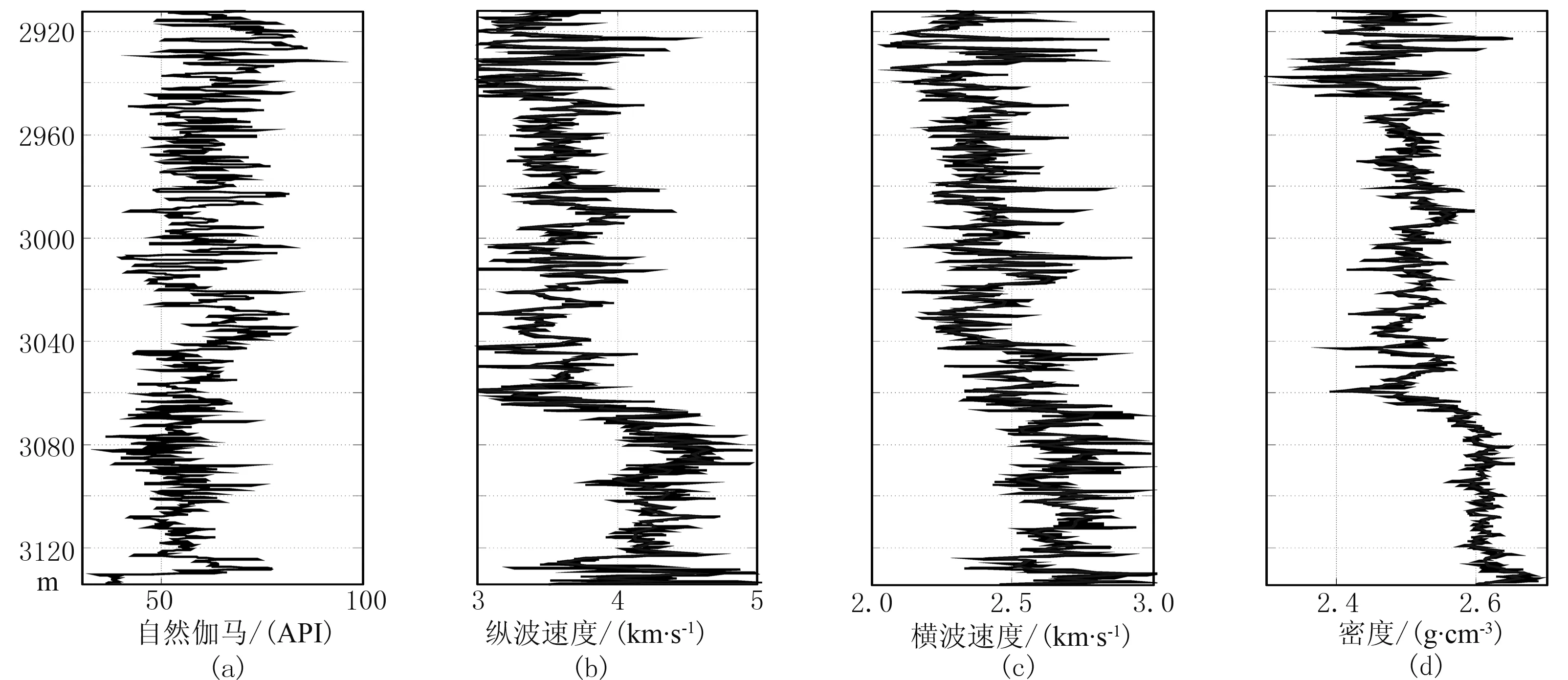
图3　罗家地区A井及等效介质测井曲线

图4　正演模拟与井震标定结果

4.3　基于Ruger理论的水平缝密度反演

图5为过A井的叠前AVO角道集，图6为目标层时窗范围，图7为过A井剖面目标层AVO曲线。由图可见，目标层具有I类AVO特征，即零炮检距振幅强且为正极性，AVO呈递减趋势，当入射角足够大时可观察到极性反转。图8为根据A井的数据设计的目标层反射模型。由图可见，反射模型为以目标层为反射界面的单界面层状模型，上覆层为低速VTI页岩，下伏层为高速各向同性灰岩。

图5　过A井的叠前AVO角道集

图6　反演时窗范围选择

图7　过A井剖面目标层AVO曲线

图8　根据A井的数据设计的目标层反射模型

图9　不同ε值的反射振幅随入射角变化曲线

应用Ruger理论，改变P波各向异性参数ε值计算该反射模型的AVO反射振幅曲线，得到不同ε值的反射振幅随入射角的变化曲线(图9)，可见随着ε的增加，反射振幅在远炮检距逐渐减小，为页岩各向异性参数反演提供了依据。地震反演方法首先要求解式(12)中的超定矩阵。图10为反演的目标层参数。由图可见，在A、B和 C三口井位处，各向异性参数ε分别为0.0923、0.3038和0.2526(图10c)，水平缝密度分别为0.0428、0.0072和0.0547(图10d)。

图11为各向异性参数反演结果，图12为各向异性参数ε与水平缝密度εH交会图，由ε、εH的关系可获得目标层水平缝密度的空间分布(图10d)。 油气开发资料表明，罗家地区C井的产量大于A井和B井，与C井的水平缝密度最大相吻合(图10d)，证明利用反演的水平缝密度进行储层预测的有效性。

图10　反演的目标层参数

图11　各向异性参数反演结果[28]

图12　各向异性参数ε与水平缝密度εH交会图

5　结束语

本文针对页岩油储层裂缝进行地震响应模拟及分析，基于VTI介质反射理论，提出了页岩含油储层各向异性参数AVO反演方法，并结合岩石物理分析结果，进一步计算储层裂缝的空间分布，得到以下认识。

(1)应用Backus平均方法将模型从测井尺度粗化至地震尺度，应用各向异性传播矩阵方法模拟及分析页岩含油储层的地震AVO响应，并结合实际地震资料进行井震标定。同时，在Ruger理论计算中发现，随着模型中各向异性参数ε数值的增大，远炮检距反射振幅逐渐减小。

(2)由地震反演得到的各向异性参数和水平缝密度与岩石物理的计算结果一致，验证了反演方法的正确性。同时，由反演得到的水平缝的空间分布与油气产量具有相关性，说明该方法在页岩油有利储层预测中的有效性。

附录A

式(2)中的传播矩阵A1和A2分别为

(A-1)

A2=iω×

(A-2)

(A-3)

(A-4)

W=p55(γsx+βsz)

(A-5)

Z=βp13sx+γp33sz

(A-6)

而

(A-7)

式中：变量ρ、γ、W和Z的下标P、S分别对应准纵波、准横波，1、2分别对应上、下层介质； pv(·)意为取复数的主值； 参数pij为6×6阶弹性刚度系数矩阵的系数。对于γ，符号“+”对应准P波，符号“-”对应准S波；sx为水平波慢度

(A-8)

其中

E={[(p33-p55)cos2θ-(p11-p55)sin2θ]2+

(A-9)

sz为垂直波慢度

(A-10)

(+,-)对应向下传播准P波， (+,+)对应向下传播准S波， (-,-)对应向上传播准P波， (-,+)对应向上传播准S波。其中

(A-11)

(A-12)

(A-13)

传播矩阵Bα=T(0)T-1(hα)，其中

(A-14)

P波入射向量为

iP=iω[βP1,γP1, -ZP1,-WP1]T

(A-15)

[1]丁文龙,许长春,久凯等.页岩裂缝研究进展.地球科学进展,2011,26(2):135-144.

Ding Wenlong,Xu Changchun,Jiu Kai et al.The research progress of shale fractures.Advances in Earth Science,2011,26(2):135-144.

[2]王健,石万忠,舒志国等.富有机质页岩TOC含量的地球物理定量化预测.石油地球物理勘探,2016,51(3):596-604.

Wang Jian,Shi Wanzhong,Shu Zhiguo et al.TOC content quantitative prediction in organic-rich shale.OGP,2016,51(3):596-604.

[3]谢剑勇,魏建新,狄帮让等.页岩各向异性参数间关系及其影响因素分析.石油地球物理勘探,2015,50(6):1141-1145.

Xie Jianyong,Wei Jianxin,Di Bangrang et al.Correlation of anisotropic parameters and their influence factors.OGP,2015,50(6):1141-1145.

[4]苏建龙,屈大鹏,陈超等.叠前地震反演方法对比分析——焦石坝页岩气藏勘探实例.石油地球物理勘探,2016,51(3):581-588.

Su Jianlong,Qu Dapeng,Chen Chao et al.Application of pre-stack inversion technique for shale gas in Jiaoshiba gas field.OGP,2016,51(3):581-588.

[5]牛聪,刘志斌,王彦春等.应用地球物理技术定量评价辽西凹陷沙河街组烃源岩.石油地球物理勘探,2017,52(1):131-137.

Niu Cong,Liu Zhibin,Wang Yanchun et al.Quantitative evaluation of Shahejie formation source rocks in Liaoxi Sag with geophysical approaches.OGP,2017,52(1):131-137.

[6]慈兴华,刘宗林,王志战.罗家地区泥质岩裂缝性储集层综合研究.录井工程,2006,17(1):71-74.

Ci Xinghua,Liu Zonglin,Wang Zhizhan.Composite study on fractured reservoir of argillaceous rock in Luojia Area.Mud Logging Engineering,2006,17(1):71-74.

[7]尹克敏,李勇,慈兴华等.罗家地区沙三段泥质岩裂缝特征研究.断块油气田,2002,9(5):24-27.

Yin Kemin,Li Yong,Ci Xinghua et al.Study on characters of muddy fractural reservoirs in Luojia Area.Fault-Block Oil & Gas Field,2002,9(5):24-27.

[8]Cheng C H.Seismic velocities in porous rocks: Direct and inverse problems.Massachusetts Institute of Technology,1978,42(1):143-144.

[9]Cheng C H.Crack models for a transversely anisotropic medium.Journal of Geophysical Research Atmospheres,1993,98(B1):675-684.

[10]Guo Z,Li X Y,Liu C.Anisotropy parameters estimate and rock physics analysis for the Barnett Shale.Journal of Geophysics & Engineering,2014,11(6):65006-65016.

[11]Hudson J A.Overall properties of a crack solid. Mathematical Proceedings of the Cambridge Philosophical Society,1980,88(2):371-384.

[12]Hudson J A.Wave speeds and attenuation of elastic waves in material containing cracks.Geophysical Journal International,1981,64(1):133-150.

[13]Schoenberg M.Reflection of elastic waves from periodically stratified media with interfacial slip.Geophysical Prospecting,1983,31(2):265-292.

[14]Schoenberg M,Muir F.A calculus for finely layered anisotropic media.Geophysics,1989,54(5):581-589.

[15]Schoenberg M,Sayers C M.Seismic anisotropy of fractured rock.Geophysics,1995,60(1):204-211.

[16]Liu E,Martinez A.Seismic Fracture Characterization.EAGE Publication,Netherlands,2012.

[17]Thomsen L.Weak elastic anisotropy.Geophysics,1986,51(10):1954-1966.

[18]Rüger A.Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media[D].Colorado School of Mines,Colorado,1996.

[19]Rüger A.P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry.Geophysics,1997,62(3):713-722.

[20]Carcione J M.A model for seismic velocity and attenuation in petroleum source rocks.Geophysics,2000,65(4):1080-1092.

[21]Ran B,Sengupta M,Salama A et al.Reconstruction of the layer anisotropic elastic parameters and high-resolution fracture characterization from P-wave data:a case study using seismic inversion and Bayesian rock physics parameter estimation.Geophysical Prospecting,2009,57(2):253-262.

[22]Backus G E.Long-wave elastic anisotropy produced by horizontal layering.Journal of Geophysics Research,1962,67(11):4427-4440.

[23]Bayuk I O,Ammerman M,Chesnokov E M.Upscaling of elastic properties of anisotropic sedimentary rocks.Geophysical Journal of the Royal Astronomical Society,2008,172(2):842-860.

[24]Lindsay R,Koughnet R V.Sequential Backus averaging:Upscaling well logs to seismic wavelengths.The Leading Edge,2001,20(2):188-191.

[25]Kumar D.Applying Backus averaging for deriving seismic anisotropy of a long-wavelength equivalent medium from well-log data.Journal of Geophysics and Engineering,2013,10(9):1-15.

[26]Rokhlin S I,Wang Y J.Equivalent boundary condi-tions for thin orthotropic layer between two solids:reflection,refraction,and interface waves.Journal of the Acoustical Society of America,1992,91(1):1875-1887.

[27]Carcione J M.AVO effects of a hydrocarbon source-rock layer.Geophysics,2001,66(2):419-427.

[28]Guo Z Q,Liu C,Liu X W et al.Research on anisotropy of shale oil reservoir based on rock physics model.Applied Geophysics,2016,13(2):382-392.