基于弹性波动方程的叠后地震反演方法

周东红　李景叶　陈　莉

(①中海石油(中国)有限公司天津分公司渤海石油研究院，天津塘沽 300459； ②中国石油大学(北京)，北京 102249)

1　引言

地震反演在油气勘探与开发中发挥着十分重要的作用[1-4]。叠后地震反演方法是地震勘探界应用较广泛的反演方法之一，在实际勘探开发中也取得了较好的效果。叠后反演方法可分为递推反演、模型反演、地震属性反演、地震统计学反演和测井曲线反演等[5]。与叠前反演相比，叠后反演具有更高的计算效率和更强的抗噪性，一直以来都被认为是储层识别与表征的核心技术。然而目前的叠后反演大多基于褶积模型，在各个界面单独计算反射系数，而忽略了波的传播效应以及地层厚度的影响，并且一般只能求取地下介质的弹性阻抗或者是声阻抗，难以直接获取储层的弹性参数，如纵波速度等。

众所周知，地震波在地下介质中的传播会受到传播效应的影响，例如层间多次波、表层多次波、透射损失和转换波等[6]，且在入射角大于30°时这种影响尤为明显。弹性波动方程能够进行全波场模拟，基于弹性波动方程的反演精度更高，但受计算效率、反演稳定性和地震资料品质等因素的制约，目前弹性波动方程反演还难以在实际生产中推广应用。

反射率法(The Reflectivity Method)是一种向量化的递推计算方法，是基于一维层状地球模型假设下进行全波场模拟的方法，该方法模拟的波场包括反射波、透射波、转换波和多次波，考虑了地震波相位变化、地层厚度以及透射损失的影响，计算精度高于有限差分法和射线法，而计算成本介于两者之间[7,8]。因此，利用反射率法求解弹性波动方程一维解析解进行地震反演可以提高精度并适合在实际生产中推广应用。

反射率法首先由Thomson提出，Fuchs等[9]最早将其用于合成地震记录的计算，后来经过Kennett[10，11]、Fryer[12]、Muller[13]以及Booth等[14]的研究和发展，该方法逐渐趋于成熟与完善。近年来，人们围绕反射率法开展正演和反演方法的研究。Zhao等[15]在Kennett的反射率法基础上采用Levenberg-Marquardt算法进行地震反演；Sen等[16]基于Kennett的反射率法进行正演，通过降梯度法求解反演目标函数，利用共轭梯度迭代寻优；Mallick等[17]采用Mallick理论求解波动方程，并用遗传算法进行反演；Padhi等[18]基于反射率法并利用全局和局部遗传算法预测海水温度和含盐度的分布。

然而，上述基于反射率法的反演多是基于Kennett或者其近似理论开展研究，递推计算量大，其嵌套式的计算方法使得求导过程复杂，对计算机的硬件要求高。为此，Phinney等[19]提出了一种向量化计算递推矩阵的反射率法，在很大程度上简化了计算过程，提高了计算效率，降低了计算成本。本文提出了基于改进的向量化反射率法的叠后地震反演方法，并结合贝叶斯理论，利用分辨率高、数值计算稳定性好的微分拉普拉斯分布引入模型参数的先验信息来降低反演的不适定性，提高地震反演精度，获得高信噪比和高分辨率的反演结果。

2　基于弹性波动方程的正演与分析

2.1　弹性波动方程一维解析解的求取

首先讨论利用改进的向量化反射率法求取弹性波动方程的一维解析解。为了简化求导过程，首先重写地震波层间传递算子的表达形式，将合成的地震数据由τ-p域转换至t-θ域。

根据反射率法的理论，假设地下介质由N个各向同性的水平层介质构成，自下而上各界面的序号为N+1,N,…,2,1，且在第1层介质的顶界面有一个点震源及若干个检波器。利用一个6维向量vn可以递归计算频率慢度域的总反射系数

vn=[Δ-RSPΔ-RSSΔRPPΔRPSΔ|R|Δ]T

(1)

式中： 向量vn代表第n个界面以下所有介质的总体响应；R代表反射系数；Δ为缩放因子； |R|为反射系数的行列式，没有明确的物理意义。

由于介质底界面以下是弹性半空间，在底界面处只有透射没有反射，因此第N+1个界面以下所有的响应可以表示为

vN+1=[100000]T

(2)

引入传递算子Qn，从第N+1个界面开始逐层向上递推计算，可以得到顶界面以下的总体响应

(3)

式中Qn是第n层介质的传递矩阵，可由矩阵En和Fn表达。En描述了第n层介质对地震波相位的改变，Fn描述了地震波经过第n层和第n+1层之间的界面时振幅的变化。不同于Phinney的方法，为了将数据从ω-p域转换到ω-θ域，把En改写为

(4)

式中： Δh为第n层厚度；α和β分别是第n层的纵、横波速度。

为了将数据从ω-p域转换到至ω-θ域，利用Snell定律，慢度p满足

(5)

根据v的定义，可以计算整个介质的总反射系数R(ω,θ)，与频率域子波褶积以后直接对其进行频率积分，得到的是t-θ域地震数据[20]

(6)

最后将计算获得的角度道集进行小炮检距叠加(选择0°～10°进行叠加)，获得叠后地震道

(7)

2.2　不同弹性参数对反射振幅的影响分析

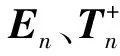
为了研究横波速度和密度对近炮检距叠加数据的影响，建立了如图1a所示的三层砂泥岩模型，并对模型进行基于反射率法正演计算，获得0°～10°的角度道集(图1b)，通过叠加获得叠后地震道(图1c)。模型中第一、三层介质为砂岩，其弹性参数相同，中间层介质为泥岩。考虑中间层介质纵波速度和密度保持不变，横波速度从1.5km/s变化到1.8km/s，以及纵横波速度不变，密度从2.1g/cm3变化到2.3g/cm3两种情况。图2为两种情况下计算的叠后地震道对比图，分析发现，尽管横波速度变化较大，合成的近炮检距叠加数据的振幅差异较小。密度变化时合成数据的振幅差异要比横波速度变化时略大，但振幅差异仍较小。模拟分析表明，横波速度和密度对小炮检距叠加数据的影响较小，利用岩石物理数据统计关系拟合横波速度和密度进而实现基于弹性波动方程叠后振幅模拟是可行的。

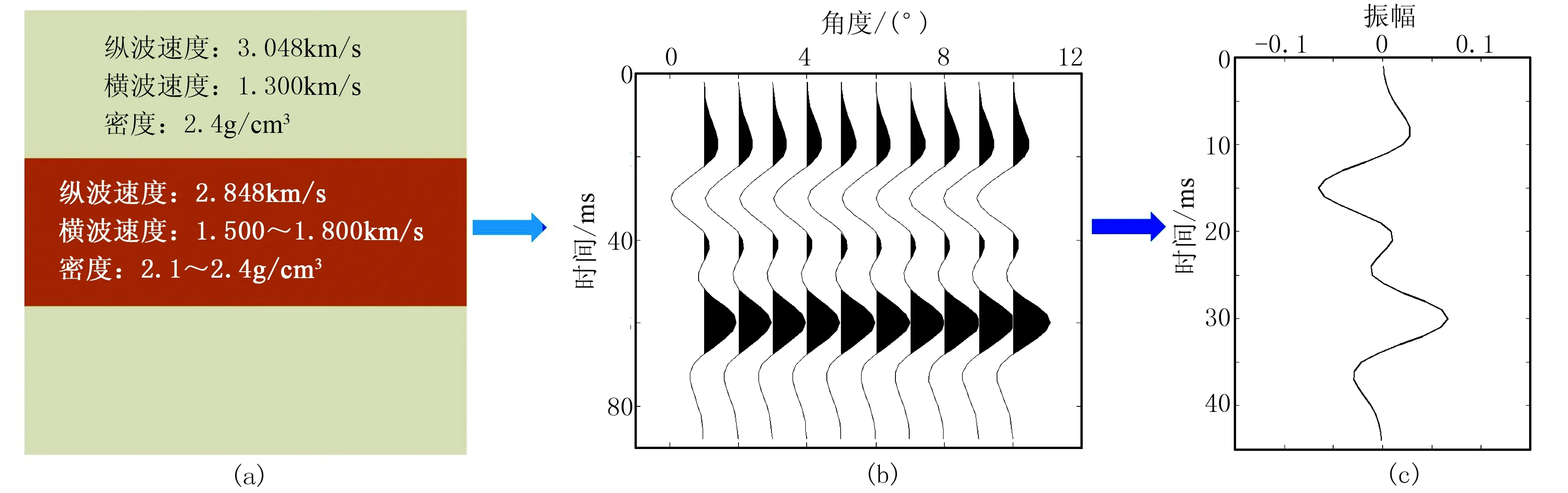
图1　三层砂泥岩模型正演流程图

图2　砂泥岩模型合成的叠加地震道

3　基于贝叶斯理论的地震反演

贝叶斯方法是用来计算条件概率的一种统计方法，可以表达为如下形式

P(m|d)∝P(d|m)P(m)

(8)

式中先验分布P(m)=P0mexp[-R(m)]，P0m视为常数项，指数项R(m)即为反演目标函数中的正则化项，其导数形式为

(9)

式中：m为真实模型参数；μ为模型参数的均值；Q*为正则化因子。

常见的先验分布有高斯分布、柯西分布等。高斯分布得到的是稳定光滑的解，有压制强反射的作用，反演分辨率不高。柯西分布虽然有较高的分辨率，但它不是凸函数，在迭代求解的过程中不能总是收敛到最优解，数值稳定性差[21]。为此，Theune等[22]率先提出了微分拉普拉斯分布，该分布具有稀疏性，是凸函数，因此数值稳定性好，纵向分辨率高。本研究引入微分拉普拉斯先验分布来约束反演过程，表示为

(10)

假设噪声满足高斯分布，那么似然函数可以表示为

P(d|m)

(11)

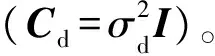
联合先验分布和似然函数可以得到后验概率分布

P(d|m)

(12)

本文直接求解最大后验概率分布解，即求解以下目标函数的极小值

(13)

由于大多数情况下正演算子G(m)为模型参数的非线性表达式，所以本文采用高斯—牛顿迭代法求解目标函数

mk+1=mk-λH(mk)-1γ(mk)

(14)

式中：λ是迭代步长；H是海森矩阵；γ是目标函数的梯度项。 为了提高计算效率，省略海森矩阵的二

阶导数项

(15)

4　模型试算

首先利用实际工区测井数据进行基于反射率法的反演测试，正演计算合成地震记录时采用主频为30Hz的雷克子波。为了拟合横波速度和密度曲线，分别统计岩石样本纵波速度与横波速度、纵波速度与密度的关系，如图3所示，统计结果为线性关系。纵波速度曲线以及拟合的横波速度和密度曲线在图4中呈现并用于后续反演。试算中首先利用这三条测井曲线进行弹性波动方程正演模拟，获得包含了多次波、转换波和透射损失影响的合成地震记录。该合成地震记录是从0°～10°的近炮检距角度道集，并将此角度道集叠加作为反演输入进行基于微分拉普拉斯先验分布的弹性波动方程反演试算。

图5为反演结果，从中可以看出本文反演的纵波速度精度较高，与实际测井曲线匹配得很好。将常规叠后反演的纵波阻抗插入图5中进行对比，分析表明，由于考虑了波传播效应的影响，本方法反演的准确性更高。为了测试方法的抗噪性，在待反演的叠加数据中加入SNR=1的随机噪声进行反演测试。反演结果表明，在此信噪比情况下本文方法的反演结果准确度较高，与实际测井曲线有较好的一致性。

图3　部分岩石样本纵波速度与横波速度(a)、纵波速度与密度(b)的统计关系

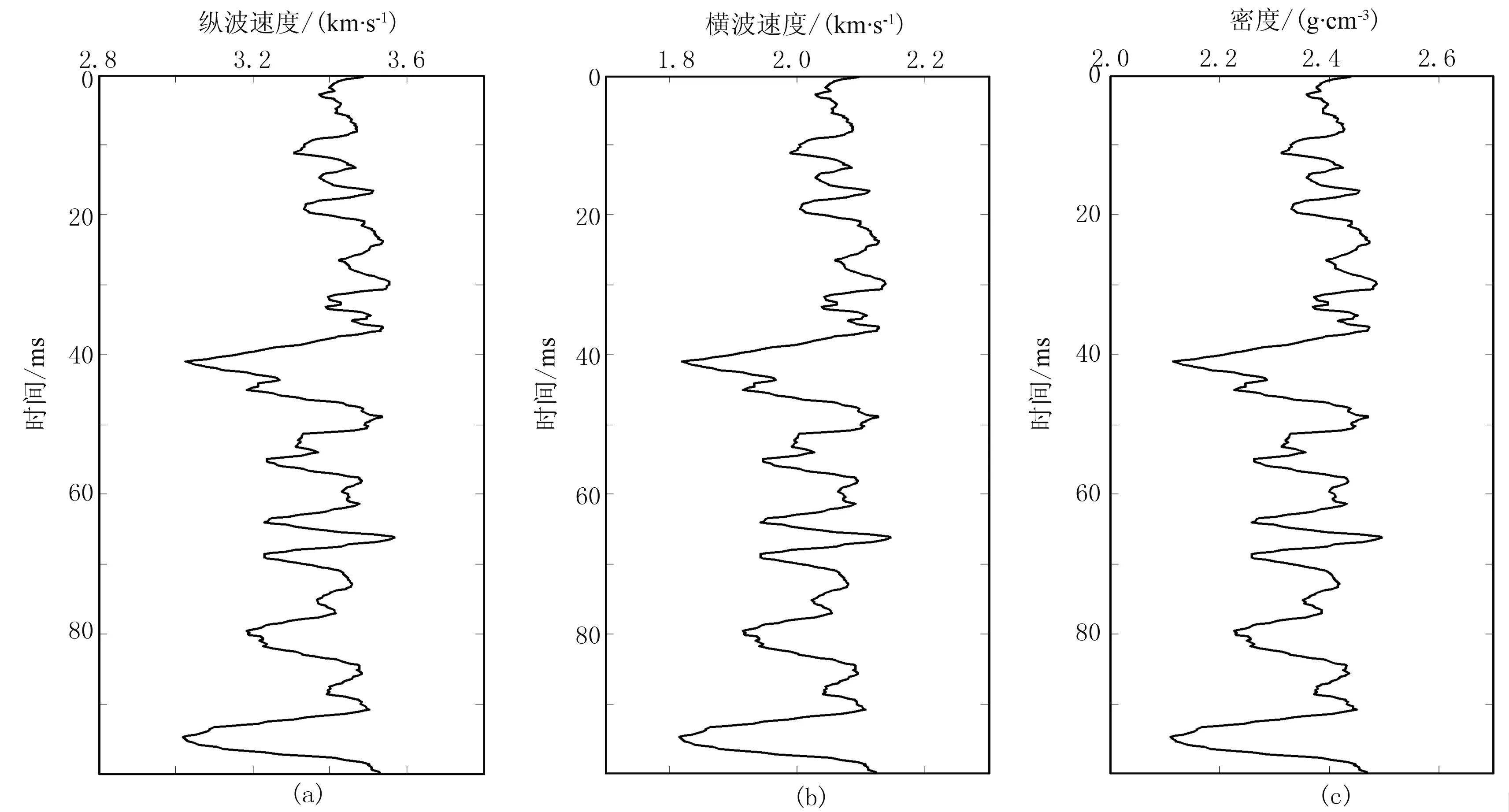
图4　拟合结果

图5　反演结果

5　实际资料试验和分析

将本文方法应用于国内某油田的实际地震数据的反演。研究区广泛发育深水湖泊沉积物，目标为古近纪时期湖泊环境下形成的构造—岩性复合油气藏。目标储层岩性为油页岩，其顶部发育砂泥岩薄互层序列。由于薄互储层的强各向异性和非均质性，地震数据受层间多次波、转换波和透射损失影响，一定程度上影响了储层的识别。

该地震数据由151个CDP组成，每一个CDP由0°～10°的近炮检距数据叠加而成，反演时窗为1900～2446ms，采样间隔为2ms。图6为CDP叠加剖面，叠加数据进行了噪声压制等处理，但没有进行层间多次波衰减、转换波去除和透射损失补偿等处理，适合本文方法反演试验。已钻井A井在CDP=33的位置。由于没有横波速度和密度的信息，本文利用工区岩石样本测试数据和其他井的纵波速度与横波速度、纵波速度与密度统计关系拟合横波速度和密度曲线，并用于后续初始模型的建立。统计关系如图7所示，已知的纵波速度曲线以及拟合得到的横波速度和密度曲线如图8所示。反演所用子波是基于测井曲线和小角度道集叠加数据提取并经过归一化处理，适用于小炮检距的反演。初始模型是利用井曲线结合井分层数据插值得到(图9)。

图10为反演获得的纵波速度剖面，能较好地刻画岩层边界，纵向分辨率高。为了验证反演结果的准确性，将本文反演的结果与常规叠后反演的波阻抗剖面进行对比，表明新方法反演的纵波速度与叠后反演的阻抗具有良好的一致性。由于引入微分拉普拉斯先验分布约束反演过程，反演的结果相对于叠后阻抗反演剖面具有更高的分辨率，地层边界更清晰。为了进一步说明反演结果的准确性，将A井处地震反演结果与纵波测井曲线进行对比(图11)，表明本文方法反演纵波速度精度较高，与实际井数据有很好的一致性。

图6　输入的CDP叠加剖面

图7　部分岩石样本的纵波速度与横波速度(a)及纵波速度与密度(b)的统计关系

图8　拟合结果

图9　建立的初始模型

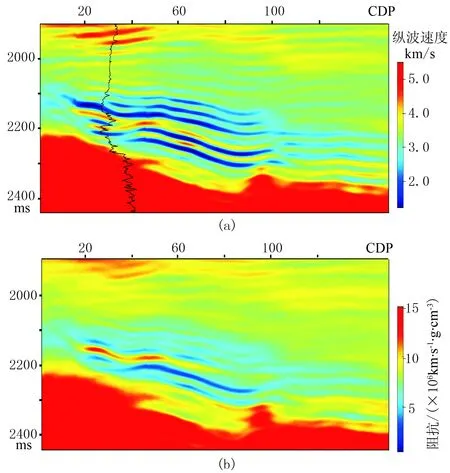
图10　反演结果对比

图11　A井处纵波速度的反演结果

6　结论和认识

本文提出了一种新的基于微分拉普拉斯先验分布的弹性波动方程叠后反演方法，模型和实际资料测试表明新方法具有以下特点：①能够考虑多次波、转换波、透射损失以及地层厚度的影响，反演精度高；②相比高斯分布和柯西分布，微分拉普拉斯先验分布可以提高反演的纵向分辨率和反演稳定性；③新方法具有较好的抗噪性，在SNR低至1时仍然能较准确地反演出弹性参数；④新方法在反演过程考虑了纵波速度、横波速度与密度等弹性参数间的关系，能够直接从叠后地震数据中反演得到纵波速度，反演结果的分辨率要高于其他类型的叠后反演。

新方法仍然存在一定的局限性：一方面本方法基于弹性波动方程理论，利用反射率法求解其解析解。反射率法是基于一维层状介质的假设，在地质构造比较简单的地区适用，但在地质构造复杂地区不适用。所以，在利用反射率法进行反演之前，需要使用深度偏移等方法使数据归位，使数据更好地接近一维层状介质假设[23]；另一方面，新反演方法基于各向同性介质理论，不适合岩石物理性质存在较强各向异性的介质，如页岩。因此，为了获得更高精度的反演效果，需要进一步研究各向异性的反射率法理论和相应的反演方法，实现各向异性介质参数预测。

[1]薛姣，顾汉明，蔡成国等.基于等效介质模型的裂缝参数AVOA反演.石油地球物理勘探，2016，51(6):1171-1179.

Xue Jiao,Gu Hanming,Cai Chengguo et al.Estimation of fracture parameters from P-wave AVOA data based on equivalent media theory.OGP,2016,51(6):1171-1179.

[2]杜泽源，吴国忱，王玉梅.基于测井约束的地震全波形反演方法.石油地球物理勘探，2017，52(6):1184-1192.

Du Zeyuan,Wu Guochen,Wang Yumei.Full waveform inversion based on well logging data constraint.OGP,2017,52(6):1184-1192.

[3]罗亚能，黄捍东，王玉梅等.地震波形反演与测井联合的三维建模方法.石油地球物理勘探，2016，51(5):947-954.

Luo Yaneng,Huang Handong,Wang Yumei et al.Three-dimensional modeling based on integration of full wave inversion and well logging data.OGP,2016，51(5):947-954.

[4]云美厚，党鹏飞，李伟娜等.地层品质因子Q值地震反演问题剖析.石油地球物理勘探，2017，52(1):189-198.

Yun Meihou,Dang Pengfei,Li Weina et al.On issues of formation quality factorQinversion.OGP,2017,52(1):189-198.

[5]撒利明，杨午阳，姚逢昌等.地震反演技术回顾与展望.石油地球物理勘探，2015，50(1):184-202.

Sa Liming,Yang Wuyang,Yao Fengchang et al.Past,present and future of geophysical inversion.OGP,2015,50(1):184-202.

[6]黄饶.薄互层气藏地震AVO研究[学位论文].北京：中国石油大学(北京)，2009，23-36.

Huang Rao.Study on AVO in Thin Interbed Gas Reservoir[D].China University of Petroleum (Beijing),Beijing，2009，23-36.

[7]Liu H,Li J,Chen X et al.Amplitude variation with offset inversion using the reflectivity method.Geophysics,2016,81(4):R185-R195.

[8]Ma Y,Loures L,Margrave G F.Seismic Modelling with the Reflectivity Method.Crewes Research Report,2004.

[9]Fuchs K,Müller G.Computation of synthetic seismograms with the reflectivity method and comparison with observations.Geophysical Journal of the Royal Astronomical Society,1971,23(4):417-433.

[10]Kennett B L N.Theoretical reflection seismograms for elastic media.Geophysical Prospecting,1979,27(2):301-321.

[11]Kennett B L N.Seismic waves in a stratified half space.Geophysical Journal International,1979,57(3):1-10.

[12]Fryer G J.A slowness approach to the reflectivity method of seismogram synthesis.Geophysical Journal International,2007,63(3):747-758.

[13]Muller G.The reflectivity method—a tutorial.Journal of Geophysics,1985,58(3):153-174.

[14]Booth D C,Crampin S.The anisotropic reflectivity technique: theory.Geophysical Journal International,1983,72(3):755-766.

[15]Zhao Huasheng,Ursin B,Amundsen L.Frequency-wavenumber elastic inversion of marine seismic data.Geophysics,1994,59(12):1868-1881.

[16]Sen M K,Roy I G.Computation of differential seismograms and iteration adaptive regularization in pre-stack waveform inversion.Geophysics,2003,68(6):2026-2039.

[17]MallickS,AdhikariS.Amplitude-variation-with-offset and prestack-waveform inversion: A direct comparison using a real data example from the Rock Springs Uplift,Wyoming,USA.Geophysics,2015,80(2):B45-B59.

[18]Padhi A,Mallick S,Fortin W et al.2-D ocean temperature and salinity images from pre-stack seismic waveform inversion methods: an example from the South China Sea.Geophysical Journal International,2015,202(2):800-810.

[19]Phinney R A,Odom R I,Fryer G J.Rapid generation of synthetic seismograms in layered media by vectorization of the algorithm.Bulletin of the Seismological Society of America,1987,77(6):2218-2226.

[20]Mallick S,Frazer L N.Practical aspects of reflectivity modeling.Geophysics,1987,52(10):1355-1364.

[21]Alemie W,Sacchi M D.High-resolution three-term AVO inversion by means of a trivariate Cauchy probability distribution.Geophysics,2011,76(3):R43-R55.

[22]Theune U,Jensås I,Eidsvik J.Analysis of prior mo-dels for a blocky inversion of seismic AVA data.Geophysics,2010,75(3):C25-C35.

[23]Buland A,Landrø M.The impact of common-offset migration on porosity estimation by AVO inversion.Geophysics,2001,66(3):755-762.