一种识别位场场源的混合小波方法

刘彩云 （长江大学一年级教学工作部，湖北 荆州434025）

重磁位场勘探方法是一种成熟的勘探手段，被广泛应用于油气勘探、金属矿勘察等领域［1，2］。场源识别是重磁资料定量解释的重要任务之一。近十几年来，连续小波变换（Continuous Wavelet Transform，CWT）被成功用于位场场源识别问题（识别场源位置和场源类型）［3～7］，该方法具有计算快速、抗噪声能力强，识别准确等优点［6］。

连续小波变换位场场源识别方法中，可选择泊松核的任意阶水平导数或垂直导数作为母小波［7］。从小波分析理论角度看，母小波的选择对场源识别结果有很明显的影响。为避免人为选择母小波的主观影响，有必要研究母小波的选择方法，提高连续小波变换识别场源的准确性。为此，笔者在前人研究的基础上，提出一种适用于无场源规模等先验信息的混合小波方法。

1 连续小波变换

在位场问题中，设观测数据用函数φ0（x）（x∈R）表示，连续小波变换定义如下［4］：

式中，a≥0是尺度因子；b∈R是位置因子；φ0（x）是被分析函数；g（x）是母小波函数；g（x）表示g（x）的复共轭；Wg｜s（b，a）是函数φ0（x）的小波变换。

Moreau等利用小波变换进行齐次场源识别的研究工作是开创性的，其主要方法步骤可概括如下。对于位于x＝0，z＝z0的齐次场源，在上半空间（a＝－z＞0）中小波变换系数满足以下双尺度关系［3］：

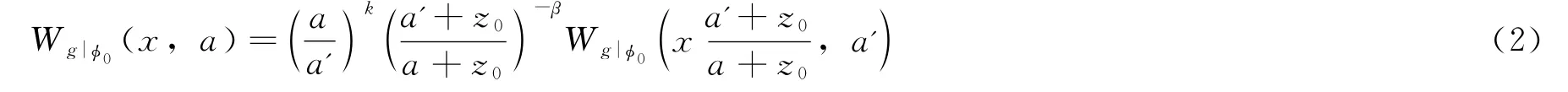
式中，β＝α－k＋1，α为场源齐次阶数；k为所选择母小波的阶数；式（2）左边位置因子和尺度因子分别为x，a；式（2）右边位置因子和尺度因子分别为x（a＇＋z0）／（a＋z0），a＇。

式（2）在（x，a）平面定义了满足z／（z0＋a）为常数的一组直线，这些直线相交于下半空间中的点（0，－z0）。从几何上看，小波变换的系数呈现出一组圆锥形结构，圆锥的顶就是场源所在的位置。

由式（2）可知，连续小波变换系数的极大值线的交点就是场源位置（齐次场源中心点的水平位置和埋深），通过选取2条能量最强的小波系数极值线，求其交点，可确定场源位置。

连续小波变换识别场源的算法步骤如下：

步1 对位场观测数据做不同尺度下的CWT，得到CWT系数矩阵；

步2 在系数矩阵中，找出极值点连成的极值线（可能为多条）；

步4 根据构成一条极值线的多个极值点，用一次多项式拟合出极值线的直线方程Wa，b＝kb＋a，其中，k为拟合出的直线斜率；

步5 求上述2条极值直线的交点，交点的横、纵坐标分别是场源的水平位置、场源深度。

2 混合小波方法

连续小波变换位场场源识别方法中，选择泊松核的导数作为母小波称为泊松小波［3］。

泊松核p（x）的定义如下：

式中，x是空间位置向量；n是观测数据维数。

在频率域，尺度为a的k阶水平泊松小波gku（u，a）、k阶垂直泊松小波gkz（u，a）分别定义如下［7］：

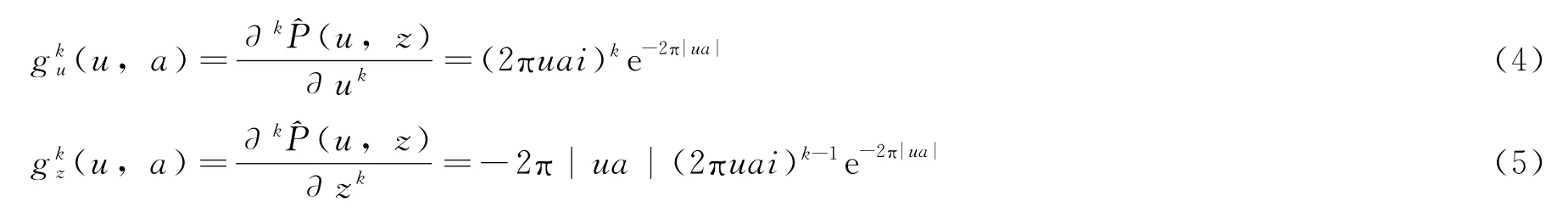
式中，u是X 方向的波数；P（u，z）是尺度为z的P（x，z）的频率域表达式。

为方便描述，以下称泊松核的k阶水平导数称为Hk母小波，k阶垂直导数称为Vk母小波。由小波分析理论可知，不同的母小波，其中心频率不同，对不同频率的信号识别能力也不同。泊松小波从H1到H5，中心频率逐步增大；从V1到V5，中心频率也是逐步增大。选用不同的母小波，会导致场源识别结果偏大或者偏小。如果能事先知道场源的规模，正确的选择母小波，则能够得到最佳的场源识别结果。

实际上，事先并不知道场源的规模，也就无法根据场源规模选择合适的母小波。为此，笔者分别采用多种母小波进行场源识别，然后计算出场源识别结果的均值和方差，以均值作为最终场源识别结果，以方差描述最终场源识别结果的可信度。这种综合采用多种母小波进行场源识别的方法笔者称之为混合小波方法（Hybrid Wavelete Method，HWM）。

3 数值试验

笔者设计如下组合模型，分析不同母小波对场源识别结果的影响。理论模型为2个不同截面大小，不同埋深的水平无限延伸的水平圆柱体。圆柱体1截面半径60m，埋深110m，水平位置＝1000m，圆柱体2截面半径10m，埋深50m，水平位置1400m。2个圆柱体的有效磁化强度1A／m，有效磁化强度倾角90°，地磁场倾角90°，有效倾角90°。

3.1 无噪声数据试验结果

分别采用H1～H5、V1～V5作为母小波，尺度因子选择为5～80，连续小波变换识别场源结果如图1所示，其中，图1（a）为理论模型的磁异常，图1（b）为连续小波变换识别场源结果。场源识别结果整理如表1所示。

从表1可以看出，由叠加的磁异常做场源识别时，对于大圆柱体场源（大尺度区域异常），无论采用何种母小波，均能够准确的识别出场源的水平位置和垂直埋深；对于小圆柱体场源（小尺度局部异常），采用不同的母小波，能准确识别小圆柱体场源的水平位置（相对误差δ≤0.36%），但场源埋深的识别结果差异较大（相对误差7.98%≤δ≤53.26%）。通过分析可知，小尺度局部异常受大尺度区域异常干扰，使其小波系数的极值线的斜率发生变化，导致深度识别产生较大误差。而当2条小波系数极值线的斜率同时变换时（例如同时变小），虽然场源深度识别结果会变小，但仍然能够正确识别出水平位置。

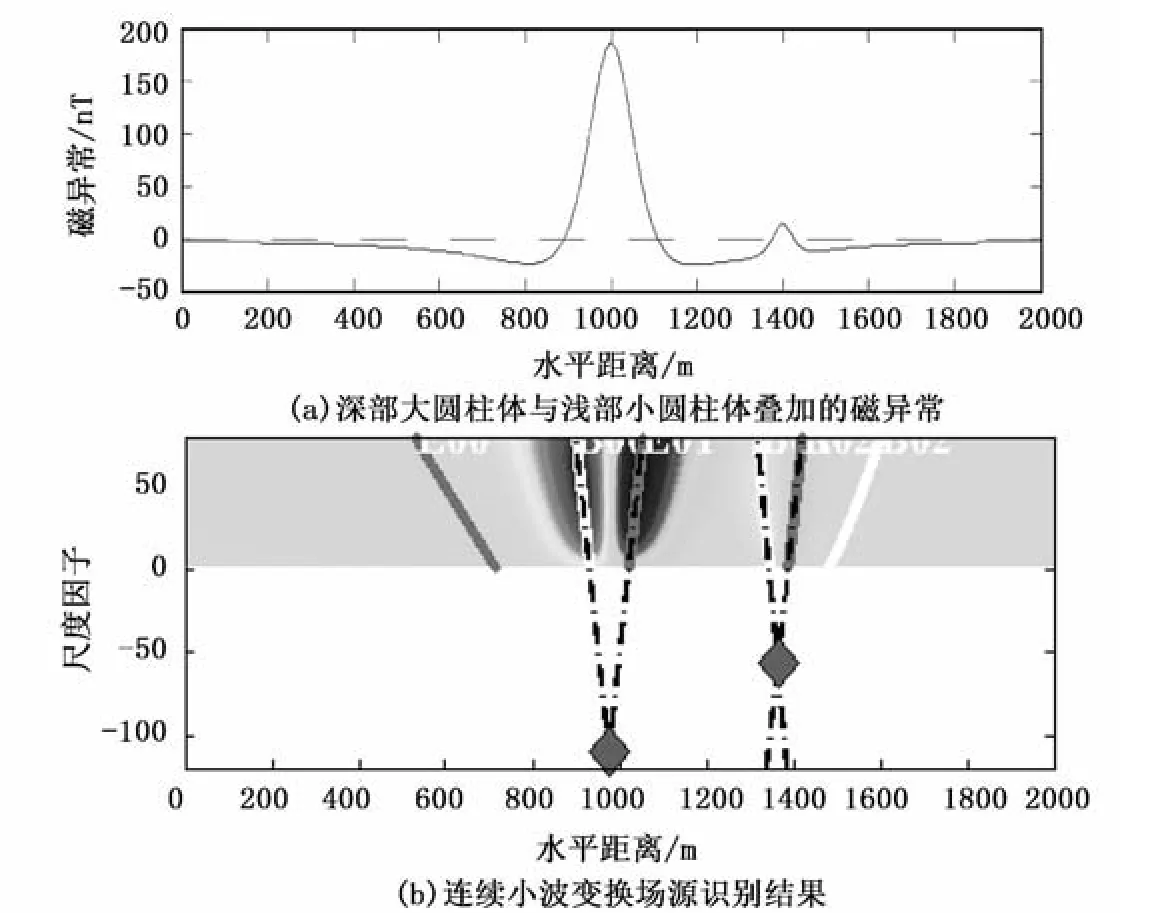
图1 连续小波变换识别叠加复杂磁异常的场源

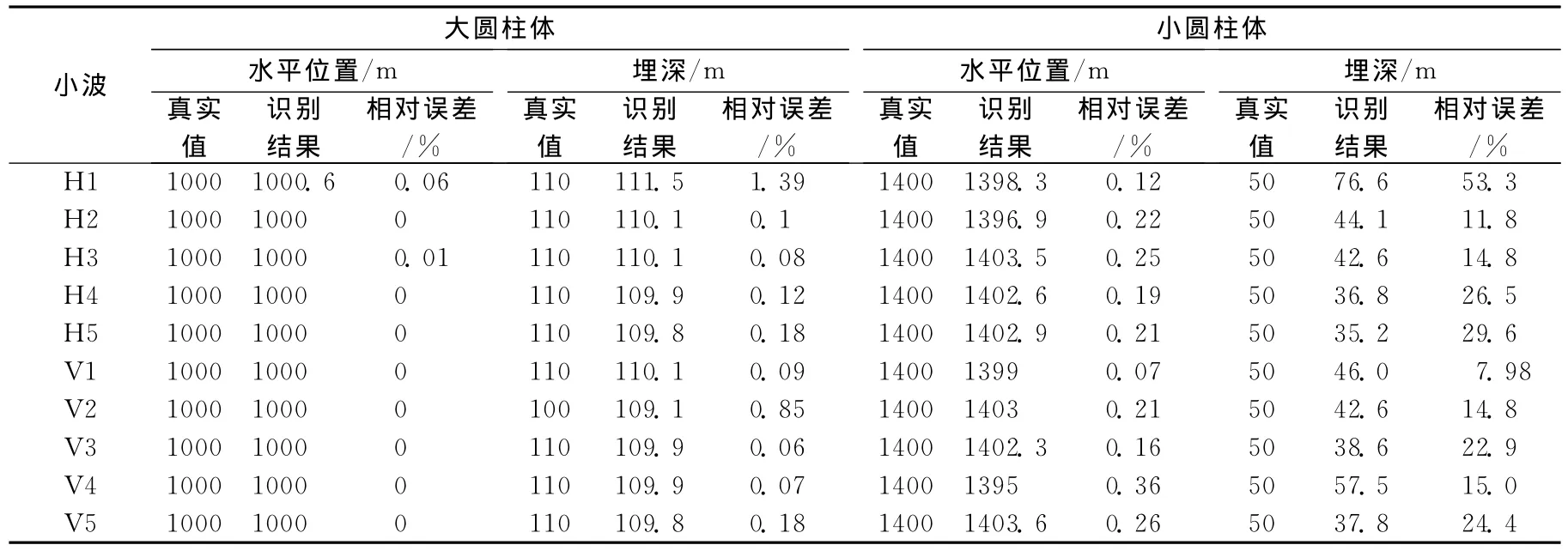
表1 理论模型无噪声观测数据采用不同母小波场源识别结果

采用HWM方法进行场源识别，结果如表2所示。对于大尺度区域异常（大圆柱体），水平位置识别相对误差为δ≤0.005%，埋深识别相对误差δ≤0.02%；对于小尺度局部异常（小圆柱体），水平位置识别相对误差δ≤0.05%，埋深识别相对误差δ≤8.45%，明显好于采用单一小波的场源识别结果。

表2 理论模型无噪声观测数据采用HWM方法场源识别结果

3.2 含噪声数据试验结果

同样采用上述理论模型，在观测数据中叠加10%的随机噪声，采用H1～H5、V1～V5母小波的场源识别试验结果如表3所示。从表3中可以看出，叠加10%随机噪声后，采用H1～H5、V1～V5母小波进行场源识别时，大圆柱体的水平位置识别相对误差δ≤0.37%，埋深识别相对误差δ≤20.6% ；小圆柱体水平位置识别相对误差δ≤0.91%，埋深识别相对误差δ≤45.5%。说明即使在有噪声情况下，不论采用何种母小波，均能够准确的识别出不同尺度、不同埋深的场源的水平位置；而选择不同的母小波，对于大尺度区域异常场源埋深识别结果影响不大，但对于小尺度局部异常场源埋深识别结果影响巨大。

采用笔者提出的混合小波方法（HWM）进行场源识别，试验结果如表4所示。通过表4可以看出，对叠加噪声后的观测数据，采用HWM方法进行场源识别，识别大圆柱体水平位置的相对误差为0.05%，标准差为1.931，识别埋深结果相对误差为5.448%，标准差为9.027；识别小圆柱体水平位置的相对误差为0.098%，标准差为6.157，埋深识别结果相对误差为5.890%，标准差为12.811。表明叠加噪声后，HWM方法仍然能够较准确的估计出不同大小、埋深的异常体的水平位置和垂直埋深。比较无噪声数据识别结果（见表2）与10%噪声数据识别结果（见表4）可以看出，两者识别结果的相对误差、标准差均相差不大，说明HWM方法具有很强的抗噪声能力。

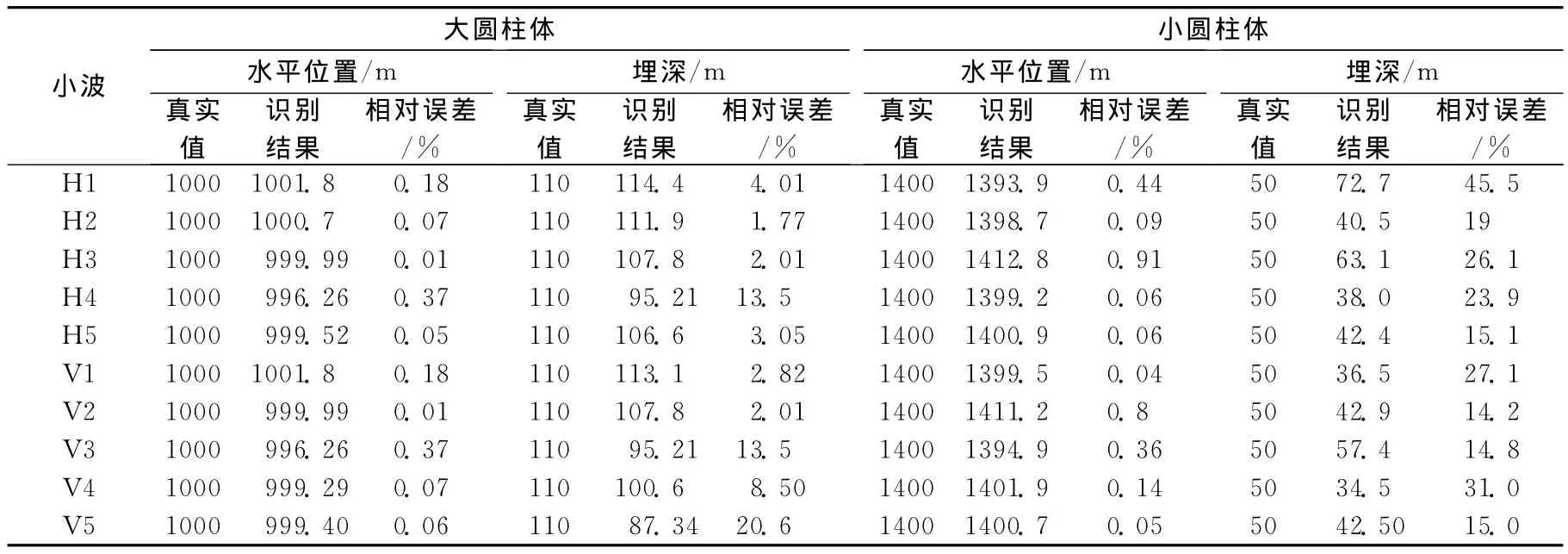
表3 理论模型观测数据叠加10%随机噪声后采用不同母小波场源识别结果

表4 理论模型叠加10%随机噪声观测数据采用HWM方法场源识别结果

4 结论

选用不同的母小波开展连续小波变换场源识别结果工作，研究不同母小波对识别结果的影响，得到如下结论：

1）对于不同埋深、不同尺度场源叠加的磁异常，小波变换场源识别方法能准确识别大尺度区域异常的场源水平位置、场源深度和小尺度局部异常的水平位置，但不能准确识别小尺度局部异常的场源深度。

2）选择不同的母小波会导致场源识别结果偏小或者偏大，混合小波方法能抵消这些影响，克服人为选择不同母小波对场源识别结果的影响，有效提高场源识别的准确度和可靠性。

3）混合小波方法对叠加噪声数据的识别结果仍然能达到较高的准确度，具有很强的抗噪声能力。

［1］Nabighian M N，Ander M E，Grauch V J S，et al，Historical development of the gravity method in exploration ［J］.Geophysics，2005，70（6）：63ND～89ND.

［2］Nabighian，M N，Grauch V J S，Hansen R O，et al，The historical development of the magnetic method in exploration ［J］.Geophysics，2005，70（6）：33ND～61ND.

［3］Moreau F，Gibert D，Holschneider M，et al，Identification of sources of potential fields with the continuous wavelet transform：Basic theory ［J］.Journal of Geophysical Research，1999，104（B3）：5003～5013.

［4］Sailhac P，Gibert D，Boukerbout H.The theory of the continuous wavelet transform in the interpretation of potential fields：a review ［J］.Geophysical Prospecting，2009，57：517～525.

［5］陈玉东.二维连续复小波变换识别重力场源 ［J］.物探与化探，2006，30（2）：141～147.

［6］刘彩云，姚长利.连续小波变换识别位场场源法的噪声影响分析与尺度因子的选择 ［J］.物探与化探，2014，38（3）：527～533.

［7］Mauri G.Multi－scale analysis of multiparameter geophysical and geochemical data from active volcanic systems ［D］.Earth Sciences－Simon Fraser University，2009 .