可控源电磁法2.5维自适应有限元各向异性正反演

粟　琪　戴世坤　赵东东

(①中南大学地球科学与信息物理学院，湖南长沙 410083；②中南大学有色金属成矿预测与地质环境监测教育部重点实验室，湖南长沙 410083)

1　引言

随着频率域可控源电磁法和计算机技术的不断发展，二维和三维电磁场的数值模拟及反演得到了很大的重视，而2.5维表现为地球物理模型的二维性和场源的三维性，相比于二维场源模拟更加接近于实际场源勘探的结果。早期关于2.5维可控源电磁法的研究大多基于各向同性介质，Coggon[1]首先把有限单元法应用于2.5维电磁法的模拟中； Stoyer等[2]利用有限差分法进行频率域2.5维磁偶极子源电磁响应的正演模拟； Doherty[3]运用积分方程法求解2.5维磁偶极子源的电磁响应； Unsworth等[4]基于有限元详细研究了2.5维电性源激发产生的电磁场响应特征； Torres等[5]提出了一种2.5维数值模拟的快速算法； Mitsuhata[6]实现了基于总场的可控源电磁法2.5维正演模拟，利用网格单元场函数插值公式与等参单元有效模拟了地形；Li等[7-9]等基于非结构化三角网格、采用预制条件的共轭梯度法和准最小残差法求解方程，实现了2.5维海洋电磁自适应有限元正演模拟； 柳建新等[10]重点研究了基于双二次插值的频率域可控源电磁法有限元正演模拟，并对波数选取进行研究，给出了一组兼顾计算速度和模拟精度的波数； Unsworth等[11]在有限元正演的基础上提出了一种子空间海洋可控源电磁的二维反演算法，引入二维OCCAM算法并得以成功应用；Abubakar等[12]研究了2.5维低频电磁法正反演，实现了一种快速可靠的反演算法； Key等[13-15]基于自适应有限元提出了面向目标的2.5维可控源电磁法正演算法，并在此基础上发展了Occam的反演算法； 陈光源等[16]实现了2.5维海洋可控源电磁法的共轭梯度反演，探讨了2.5维海洋可控源电磁法的不同反演算法，并分析了不同参数对反演速度及精度的影响。

目前研究各向异性介质可控源电磁法数值模拟和反演计算的文献并不多。Li等[17,18]研究了均匀半空间各向异性介质情况下的CSAMT响应，并分析了视电阻率与地下真实电阻率的关系； Loseth等[19]提出了一种模拟层状各向异性介质中波数域水平电偶极源产生的电磁场的算法； 罗鸣等[20,21]探讨了一维电阻率各向异性对海洋可控源电磁响应的影响，并实现了一维垂直各向异性介质频率域海洋可控源电磁资料的反演； Kong等[22]运用有限元法进行水平各向异性条件下的2.5维海洋可控源电磁法数值模拟； Li等[23]采用自适应有限元法实现了倾斜各向异性情形下基于二次场的二维海洋可控源电磁法的正演算法； 刘颖等[24]详细研究了层状各向异性介质中任意取向电偶源的海洋电磁响应以及不同发射姿态对勘探能力的影响； 赵东东[25]研究了任意各向异性介质中2.5维可控源电磁法正演模拟算法及观测系统的设计。

本文从各向异性的二维地电模型出发推导出基于总场的三轴各向异性的耦合微分方程组，避免了二次场计算时繁杂的地形计算问题。文中采用基于非结构化网格的自适应有限元法求解正演控制方程组，网格由仅局部加密而不改变插值函数阶次的h型自适应策略生成[26]，参考开源程序MARE2DEM的正演部分算法，使用KDTree管理数据以提高自适应过程中对节点和单元访问的效率。此外，对正演算法程序做了并行化处理以提高计算效率，并调用MKL库中Pardiso_64位求解器求解大型稀疏复线性方程组，然后在理论模型算例计算中分别与一维解析解和MARE2DEM计算结果进行对比，验证了本文正演算法具有较高的计算精度和计算效率。反演时采用对初始模型要求较低的Occam反演算法，并设计了多个典型的各向异性地电模型进行反演计算； 最后通过实测数据对本文反演算法进行了验证。

2　方法理论

2.1　正演理论

2.1.1各向异性介质的2.5维问题

考虑具有一般性的各向异性的二维导电模型，设结构走向为y，x方向轴水平向右，z轴垂直向上。假定时谐因子为eiω t，则带源的频率域麦克斯韦方程为

(1)

(2)

(3)

(4)

式中:E是电场强度；H是磁场强度；MS为外加源的等效磁化强度;JS为外加源的电流密度; 下标“S”代表源；σ是任意各向异性的电导率张量；ε是任意各向异性的介电常数张量；=iωμ为阻抗率，μ为磁导率。式(1)和式(2)为三维方程，沿构造走向 做傅里叶变换得到二维方程。联立变换后的偏微分方程，可得到关于两个平行于走向的电磁场分量和的耦合微分方程

(5)

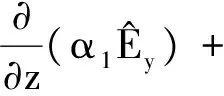
(6)

(7)

(8)

其他系数是与波数和电导率张量有关的函数，具体表达式如下

(9)

(10)

(11)

(12)

(13)

(14)

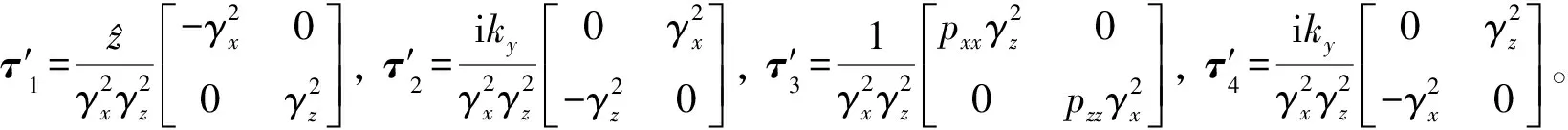
2.1.2自适应有限元算法

模型的网格剖分对正演模拟结果的精度有重要影响，而依靠经验进行网格剖分仅适用于简单的地电模型，对于实际勘探中不清楚的地下构造复杂模型，通常难以进行合理可靠的网格剖分。自适应有限元法能够自动细化网格并在不显著增加计算时间的条件下提供可靠的计算结果，是一种能够自动调整算法以改进求解过程的数值方法。自适应有限元法主要包括偏微分方程求解、误差估计、网格标记和网格优化四个步骤，而其中研究重点是误差估计和自适应网格优化。

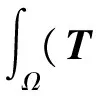
(15)

式中：T和C为耦合微分方程式(13)和式(14)的系数矩阵；f为源项向量。为简化表述，令

(16)

则式(15)的离散形式可表示为

B(un,v)=F(v)

(17)

式中：u为精确解；un为有限元数值解。令全局误差估计算子ξn≈u-un，由于精确解u无法预知，所以全局误差估计算子不能直接求解，可通过近似误差函数计算

B(ξn,v)=B(u-un)=F(v)-B(un,v)

(18)

由于二维电磁对于沿走向方向的场及其空间梯度的精确度有较高的要求，参考Key等[13]定义的误差函数

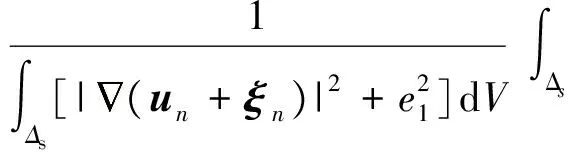
(19)

式中：e0和e1是两个调节误差函数的常数[13]； Δs表示包含接收点的可能不连续区域的三角单元。利用加权余量法计算得到耦合方程的有限元解un，然后通过式(18)求解全局误差估计算子ξn， 代入式(19)计算误差函数G，将G值代入B(v,wn)=

G(v)，求出B(un,v)的对偶解wn，通过B(v,δn)=G(v)-B(v,wn)得到对偶解的离散误差δn，最后计算出三角形单元△的局部单元误差指示因子uΔ=|F(δn)-B(un,δn)|。

根据计算的误差因子对网格进行恰当的优化，加密局部网格以增加有限元解的精度。本文的网格优化方法采用的是Delaunay三角约束剖分程序Triangle[27]，该程序使用Ruppert网格优化策略，主要是通过增加节点数直到所有三角单元满足权重约束从而更新和优化网格。对于最初产生的粗网格，求解相应的有限元解，计算每个单元上的局部误差指示因子u△，标记误差较大的单元以便进行优化，产生新的细化网格并在该网格上重新求解偏微分方程，再次计算u△并标记需要细化的网格单元，重复上述四个步骤直至误差泛函满足设定的要求，其算法流程如图1所示。

图1　自适应有限元正演模拟算法流程图

2.1.3灵敏度计算

灵敏度直接影响反演的精度和效率，目前常用的有Rodi算法、互易原理和伴随方法[28]。伴随方法通过设置合理的伴随源，计算其产生的伴随电磁场，对伴随电场与真实场电场的点积进行积分来计算电磁场分量U与模型电导率σj的偏导数，在此用通式U表示电场或磁场。McGillivray等[29]、Unsworth等[11]、Farquharson等[30]对该方法进行了详细论述，并将其应用于二维电磁问题。刘颖[28]、Key[31]分别将伴随方法应用于各向同性和三轴各向异性介质2.5维海洋可控源电磁法正反演计算中。在模型参数个数大于接收点数量时，利用伴随方法计算效率相对最高。

本文利用上标“a”表示引入伴随源产生的相关量，对于有限区域D，通过添加伴随场，灵敏度可由如下公式计算

(20)

通过设置恰当的伴随源即可求出电磁场分量U对电导率的偏导数

(21)

对于2.5维问题，沿走向y方向无限延伸，对于电导率为σj的单元，积分区域为Aj，故上式可写成

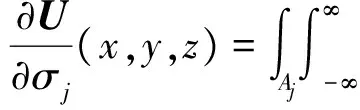
(22)

其中

(23)

定义

(24)

将式(23)代入式(22)，并分别对y和ky求积分，将式(24)代入，可得灵敏度计算公式

(25)

式中，yr和ys分别表示沿走向方向的接收点和源的位置。

2.2　反演算法

反演算法采用基于高斯—牛顿法改进的Occam算法[32]，基于正则化反演策略的目标函数为

Φ=μ(λ‖Rm‖2+β‖m-m*‖2)+

(26)

对于给定的初始模型m(k)，为使目标函数最小，新的迭代模型m(k+1)为

m(k+1)=[μRTR+(WJ(k))T(WJ(k))]-1×

(27)

(28)

模型粗糙度算子R通过提供对模型变化的衡量促使反演稳定，并使目标函数在最小化的过程中避免反演出虚假结构。对于非结构化三角网格，粗糙度范数取为

(29)

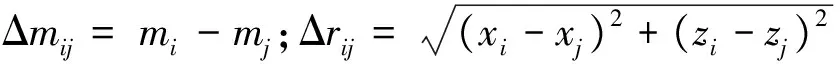
反演迭代过程通过计算模型修改量Δm确定新的模型m(k+1)，计算并判断模型正演响应与观测数据之间的拟合差是否达到要求，实现对目标函数Φ最小化的求解。

3　正演算法测试

3.1　算法验证

为验证正演算法的正确性，设计如图2所示的4层VTI介质模型，使用本文正演算法计算其正演响应，并分别与解析解和MARE2DEM计算结果进行对比。其中：第一层介质为电阻率为0.33Ω·m的海水层，厚度为200m;第二层介质厚度为800m，

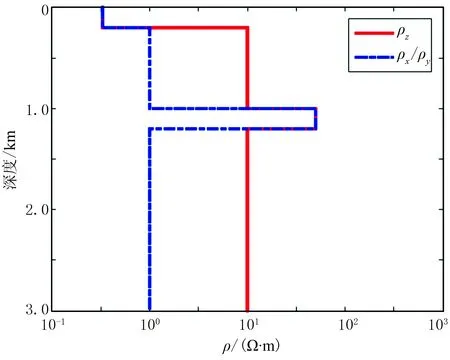
图2　一维VTI介质模型示意图

电阻率分别为ρx=ρy=1Ω·m,ρz=100Ω·m； 第三层介质电阻率为50Ω·m，厚度为200m；最下层介质电阻率与第二层一致。发射源置于150m深度，发射频率为0.5Hz， 120个接收机在水平方向-10～10km范围内均匀分布，位于海底上方0.1m处。将本文计算的电磁响应与解析解进行对比，结果如图3所示。水平各向异性介质正演数值解与解析解吻合得很好，相对误差均在1%以下。本文算法与MARE2DEM在运用自适应有限元求解2.5维电磁问题时都是基于总场离散，与MARE2DEM计算结果进行对比，结果如图4所示，可见相对误差相对较小。

图3　一维VTI介质模型响应对比图

图4　本文算法与MARE2DEM计算结果对比

3.2　计算效率

参考Li等[23]设计的各向异性海洋油气藏模型(图5)，空气电阻率取为1.0×1012Ω·m，空气下方为电阻率0.3Ω·m、深度为1km的海水层。采用电偶极源，发射频率为0.25Hz，发射电流为1A，发射源位于海底上方50m的海水中，接收装置均匀放置在海底上方0.1m的海水中。

假设海底地层围岩为各向异性介质ρw， 其中各主轴电阻率分别取ρwx=ρwy=1.0Ω·m，ρwz=8.0Ω·m，异常体为各向同性的高阻油气藏位于海底以下1km处，电阻率为ρa=50Ω·m。 针对上述模型进行正演，网格采用算法中的自适应网格剖分，由于沿海底地形加密测点，模型正演初次优化网格剖分为由3328个节点组成的6552个三角形单元，

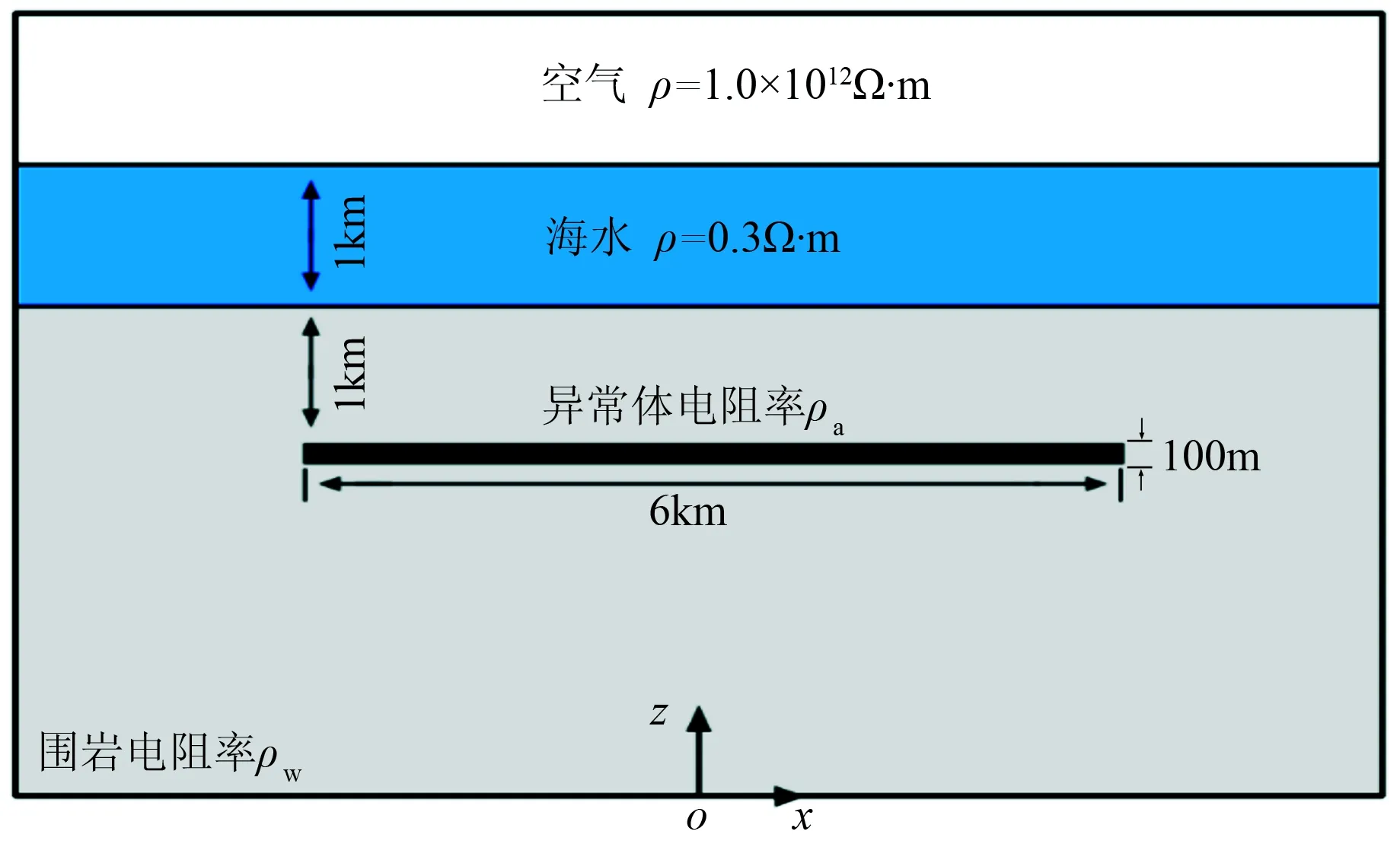
图5　二维各向异性介质模型示意图

剖分网格的中间部分如图6a所示； 自适应网格优化共经过7次细化剖分，最终产生了17189个节点和34267个三角形单元，如图6b所示。可以看出，由于测点附近空间剖分对正演响应的计算精度影响较大，所以在创建正演模型时对测点附近的网格进行了加密，使得剖分的初始网格在测点附近已经占据了较多单元。从自适应细化的过程可以看出，经过7次网格优化，深部的粗网格没有进行太多的加密，而源和测点附近及异常体边界的网格得到了加密。

快速、高精度的正演是反演的基础，而线性方程的求解占据了正演计算的大部分时间，自适应有限元法在对网格进行优化之后需要计算单元误差因子，相对于传统有限元其不仅增加了线性方程组的求解次数，还可能增加线性方程组的维数。因此，含有大型稀疏矩阵的线性方程组的稳定、快速求解是正演的关键。网格的每一次自适应优化，都会增加线性方程组的行数。图7a～图7c展示的三个稀疏矩阵取自于自适应正演过程中线性方程Ax=b中的左端项矩阵A，随着网格优化其矩阵维数明显增加。为验证本文程序在求解大型稀疏矩阵线性方程组时的性能，选取每次网格优化后的线性系统，在设置OpenMP线程为1的情况下，分别调用并记录本文程序AFEM2D所用的Pardiso求解部分算法与MARE2DEM的Umfpack求解部分算法的耗时，结果如图7d所示。可以看出，Pardiso在求解大型稀疏矩阵线性方程组时求解速度相对较快，尤其是稀疏矩阵维数比较大的时候相对于MARE2DEM使用的Umfpack具有一定优势。

图6　正演自适应网格剖分示意图

4　反演算法测试

4.1　合成数据测试

为验证算法的准确性和可靠性，设计如图8所示的复杂各向异性介质模型，模拟真实构造。设海底为起伏地形，海水电阻率为0.3Ω·m，海底表层为一与海底地形同样起伏、厚度约为500m的覆盖层，电阻率为0.7Ω·m； 覆盖层下方为一正断层，上盘、下盘介质电阻率分别为2.0Ω·m和4.0Ω·m，厚度为1.5～2.0km。上盘中赋存有各向异性的异常体D，其三个主轴方向的电阻率分别为：ρx=80Ω·m、ρy=ρz=2Ω·m，即异常体D仅在x方向表现出电阻率异常。断层下方存在A、B和C三个电阻率为1000Ω·m的高阻异常体； 基岩电阻率为100Ω·m； 其上方沉积层电阻率为1Ω·m，厚度约为2km。

图8　二维各向异性海洋模型

反演所用的观测数据采用自适应有限元正演响应加上4%高斯随机噪声的合成数据；正演采用电偶极发射源，发射频率为0.1、0.25、1.0和3.0Hz，发射源和接收装置皆均匀分布在-11～11km范围内，发射源与接收装置交错排布。发射源共65个，位于海底起伏地形上方50m的海水中，间距为346m； 65个接收装置放置在海底上方0.1m的海水中，间隔也为346m。观测数据包含电磁场分量Ex的幅值和相位，加入噪声和去除发射源附近的部分数据后共包含18288个数据点。

反演初始模型包含空气、海水和海底地层，其中空气和海水电阻率不参与反演，给定地层的初始电阻率为1.0Ω·m。计算区域所划分的单元越多，所需要的计算量越大，因此只对包含异常体的部分采用较细的剖分网格，其余部分则采用粗网格以减少不必要的计算量。如图9所示，选取x范围为-10～10km、海底起伏面到8.5km深的区域进行精细剖分，共生成25766个三角形单元，其余部分共剖分为2108个三角形单元。反演过程中针对特定的发射源、测点和频率，利用自适应有限元正演法对正演网格进行自适应网格优化，靠近源和测点位置附近的单元通常做更细的剖分，以满足正演计算的精度需求。对反演初始模型进行剖分时采用粗细网格组合的方式，对异常体可能存在的区域进行较精细的网格剖分，有利于对异常体边界的界定，而粗网格的使用可以减少不必要的计算量。

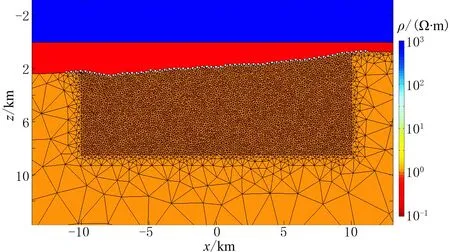
图9　反演初始模型示意图

设定目标均方根拟合差为1.0，经过13次反演迭代，最终反演模型均方根拟合差达到1.0031。在CPU为Intel i5、内存为16G的台式机上，反演总耗时为1.688×105s。反演结果如图10和图11所示，其中图10是各向异性x轴方向的电阻率反演结果，图11为各向异性y方向和z方向的电阻率反演结果。整体来看，浅部反演效果较好，海底下方地层的电阻率和厚度与模型基本一致，断层两侧地层也能较好地进行区分，对于基岩上方相对较深的沉积层，其电阻率反演结果与模型比较接近，但是由于上方高阻异常体的影响，导致基岩起伏界面不太明确，高阻异常体下方呈现相对低阻致使基岩起伏面下延。反演结果中除了各向异性异常体存在一定的误差，总体来看两图在非各向异性区域的反演结果吻合很好，很接近真实模型的地质特征。各向同性异常体A、B和C电阻率皆为1000Ω·m，反演结果中其形态范围和中心电阻率与模型都基本接近，但是还存在一定误差，其中异常体C的电阻率反演结果相对更好。对于各向异性异常体D来说，仅在x轴方向表现出电阻率异常，而y轴和z轴电阻率相对于围岩相同，从x轴方向反演结果看，尽管其电阻率和轮廓与真实模型还存在差距，但都得到了较好的还原，相对于其他主轴电阻率反演结果能够很好地识别该异常体。

图10　电阻率ρx反演结果

4.2　实测数据测试

数据源自斯克里普斯海洋学研究所Weitemey-er等[33,34]的项目，采集于美国俄勒冈州的水合物脊，该区属于距俄勒冈州西海岸约80km的近海，是卡斯卡底古陆板块汇聚边缘，它以海底蕴藏大量甲烷水合物著称，该地区流体、气体喷发活跃，有巨大的硫氧化物细菌和蛤蚌组成的群落，存在大量的自生碳酸盐岩。测线处海水深度约800～1200m。采用一个拖曳式水平电偶极子源进行59次发射，发射源位于海底上方约100m的海水中，发射频率固定为5Hz，接收装置由线性排布的25个接收机组成，测点间距约为600m，测点位置如图12所示。

图11　电阻率ρy/ρz反演结果

图12　测点位置示意图

根据测点和发射源的位置大致建立海底地形，对实测数据进行带地形的各向异性反演。由于建立地形过程中的手动误差，初始模型中测点与海底地层之间距离与实际情况存在差距，因此也可能给反演带来一定的误差。本文反演的自适应性体现在其所采用的自适应有限元正演引擎。反演初始模型网格的粗细只影响反演结果中异常体边界的识别，理论上精细网格能够更加精确地限定异常体，但是也会使得初始模型的划分单元过多而增加计算时间，且反演过程本身是对初始模型各单元电阻率的不断估计，因此要求反演迭代过程中模型单元数保持一致。对于实测数据，初始模型应根据测区地质情况和勘探任务建立，本例中初始模型和网格剖分如图13所示，由于天然气水合物通常赋存于水深几百米的沉积层中，所以初始模型仅对浅部进行细化剖分，其余部分采用粗网格。设定初始模型为三轴各向同性介质(ρx=ρy=ρz=1.0Ω·m)，网格共剖分为4732个节点、27447个三角单元。

反演经8次迭代，耗时7.35×104s，反演模型均方根拟合差为6.095，反演结果如图14所示。可以看出，三个轴的电阻率反演结果非常接近，说明该测线处地下水合物应该是近似于电性各向同性的。反演结果中A、B、C和D四处电阻率在对数化处理后依然存在相对高阻异常，根据此处地质环境的情况，推断上述四处应该是天然气水合物或游离气，与Weitemeyer等[34]基于有限差分法和有限元正演反演的研究结果基本一致。

图13　实测数据反演初始模型剖分示意图

图14　实测数据电阻率反演剖面图

5　结束语

本文针对各向异性介质中的2.5维可控源电磁场正反演问题，从各向异性二维导电模型出发到三轴各向异性的耦合微分方程的推导，使用基于非结构网格的自适应有限元法求解正演控制方程，反演算法采用对初始模型要求较低的基于高斯—牛顿法改进的Occam反演算法。对一维VTI介质模型和经典高阻油气藏模型进行正演计算，利用自适应有限元算法进行网格优化加密，将计算结果与一维解析解和MARE2DEM结果进行了对比，验证了计算精度和计算效率；对于赋存有各向异性异常体的复杂海洋模型，由于非结构化三角单元网格具有模拟地形和复杂构造的优势，除了反演出各向同性介质的构造，还比较真实地还原了各向异性异常体的形态、大小和埋深；对实测数据给定各向异性初始模型进行了反演，与已有文献的研究结果对比，证明了反演算法能比较成功地还原模型的主要电性特征。目前本研究还存在一定局限性，仅推导了任意倾斜各向异性介质的情况，今后将会把主轴与构造走向夹角加入各向异性正、反演算法中。

[1]Coggon J H.Electromagnetic and electrical modeling by the finite element method.Geophysics,1971,36(2):132-155.

[2]Stoyer C H and Greenfield R J.Numerical solutions of the response of a two-dimensional earth to an oscillating magnetic dipole source.Geophysics,1976,41(3):519-530.

[3]Doherty J.EM modeling using surface integral equations.Geophysics,1988,53(6):644-668.

[4]Unsworth J M,Bryan J T,Alan D C.Electromagnetic induction by a finite electric dipole source over a 2-D earth.Geophysics,1993,58(2):198-214.

[5]Torres V C,Habashy T M.Rapid 2.5D forward mode-ling and inversion via a new nonlinear scattering approximation.Radio Science,1994,29(3):1051-1079.

[6]Mistsuhata Y.2-D electromagnetic modeling by finite-element method with a dipole source and topography.Geophysics,2000,65(2):465-475.

[7]Li Y.A finite-element algorithm for electromagnetic induction in two dimensional anisotropic conductivity structures.Geophysical Journal International,2002,148(3):389-401.

[8]Li Y,Key K.2D marine controlled-source electromag-netic modeling (Part 1):An adaptive finite-element algorithm.Geophysics,2007,72(2):WA51-WA62.

[9]Li Y,Constable S.2D marine controlled-source electro-magnetic modeling (Part 2):The effect of bathymetry.Geophysics,2007,72(2):WA63-WA71.

[10]柳建新，汤文武，童孝忠.基于双二次插值的2.5维FCSEM有限元正演模拟.中南大学学报(自然科学版),2014,45(2):474-482.

Liu Jianxin,Tang Wenwu,Tong Xiaozhong.Finite element forward modeling of 2.5-D FCSEM based on biquadratic interpolation.Journal of Central South University (Science and Technology),2014(2):474-482.

[11]Unsworth M,Oldenburg D.Subspace inversion of electromagnetic data:Application to mid-ocean-ridge exploration.Geophysical Journal International,1995,123(1):161-168.

[12]Abubakar A,Habashy T M,Druskin V L et al.2.5D forward and inverse modeling for interpreting low-frequency electromagneticmeasurements.Geophysics,2008,73(4):F165-F177.

[13]Key K,Ovall J.A parallel goal-oriented adaptive finite element method for 2.5-D electromagnetic modelling.Geophysical Journal International,2011,186(1):137-154.

[14]Key K.Marine EM inversion using unstructured grids:a 2D parallel adaptive finite element algorithm.SEG Technical Program Expanded Abstracts,2012，31:1-5.

[15]Myer D,Key K,Constable S.Marine CSEM of the Scarborough gas field,Part 2:2D inversion.Geophy-sics,2015,80(3):E187-E196.

[16]陈光源,杜立彬,景建恩等.2.5维海洋可控源电磁反演算法及影响参数研究.地球物理学进展,2016,31(4):1796-1802.

Chen Guangyuan,Du Libin,Jing Jian’en et al.2.5D inversion algorithm and parameters of marine controlled-source electromagnetic method.Progress in Geophysics,2016,31(4):1796-1802.

[17]Li X and Pedersen L B.The electromagnetic response of an azimuthally anisotropic half-space.Geophysics,1991,56(9):1462-1473.

[18]Li X and Pedersen L B.Controlled-source tensor magnetotelluric responses of a layered earth with azimu-thal anisotropy.Geophysical Journal International,1992,111(1):91-103.

[19]Loseth L O,Ursin B.Electromagnetic fields in planarly layered anisotropic media.Geophysical Journal International,2007,170(1):44-80.

[20]罗鸣,李予国.一维电阻率各向异性对海洋可控源电磁响应的影响研究.地球物理学报,2015,58(8):2851-2861.

Luo Ming,Li Yuguo.Effects of the electric anisotropy on marine controlled-source electromagnetic responses.Chinese Journal of Geophysics,2015,58(8):2851-2861.

[21]罗鸣,李予国,李刚.一维垂直各向异性介质频率域海洋可控源电磁资料反演方法.地球物理学报,2016,59(11):4349-4359.

Luo Ming,Li Yuguo,Li Gang.Frequency domain inversion of marine CSEM data in one dimensional vertically anisotropic structures.Chinese Journal of Geophysics,2016,59(11):4349-4359.

[22]Kong F N,Johnstad S E,Rosten T et al.A 2.5D finite element-modeling difference method for marine CSEM modeling in stratified anisotropic media.Geophysics,2008,73(1):F9-F19.

[23]Li Y G,Dai S K.Finite element modelling of marine controlled-source electromagnetic responses in two-dimensional dipping anisotropic conductivity structures.Geophysical Journal International,2011,185(2):622-636.

[24]刘颖,李予国.层状各向异性介质中任意取向电偶源的海洋电磁响应.石油地球物理勘探,2015,50(4):755-765.

Liu Ying,Li Yuguo.Marine controlled-source electromagnetic fields of an arbitrary electric dipole over a layered anisotropic medium.OGP,2015,50(4):755-765.

[25]赵东东.各向异性介质可控源电磁法2.5维数值模拟及观测系统研究[学位论文].湖南长沙：中南大学，2016.

Zhao Dongdong.Research on 2.5D Modeling and Observation System for Controlled-Source Electromagnetic Method in Anisotropic Medium [D].Central South University,Changsha,Hu’nan,2016.

[26]Kittur M G,Huston R L,Oswald F B.Mesh refinement in finite element analysis by minimization of the stiffness matrix trace.Computers & Structures,1989,31(6):891-896.

[27]Shewchuk J R.Reprint of delaunay refinement algorithms for triangular mesh generation.Computational Geometry,2014,47(7):741-778.

[28]刘颖.海洋可控源电磁法二维有限元正演及反演[学位论文].山东青岛：中国海洋大学,2014.

Liu Ying.2D Finite Element Modeling and Inversion for Marine Controlled-Source Electromagnetic Fields[D].Chinese Marine University,Qingdao,Shandong,2014.

[29]McGillivray P R,Oldenburg D W,Ellis R G et al.Calculation of sensitivities for the frequency-domain electromagnetic problem.Geophysical Journal International,1994,116(1):1-4.

[30]Farquharson C G,Oldenburg D W.Approximate sensi-

tivities for the electromagnetic inverse problem.Geophysical Journal International,1996,126(1):235-252.

[31]Key K.MARE2DEM:a 2-D inversion code for con-trolled-source electromagnetic and magnetotelluric data.Geophysical Journal International,2016,207(1):571-588.

[32]Constable S C,Parker R L,Constable C G.Occam’sinversion — A practical algorithm for generating smooth models from electromagnetic sounding data.Geophysics,1987,52(1):289-300.

[33]Weitemeyer K,Constable S,Key K et al.First results from a marine controlled-source electromagnetic survey to detect gas hydrates offshore Oregon.Geophysical Research Letters,2006,33(3):L03304.

[34]Weitemeyer K,Gao G,Constable S et al.The practical application of 2D inversion to marine controlled-source electromagnetic data.Geophysics,2010,75(6):F199-F211.