加减和乘除的区别

◇张清清 曾小平

掌握运算律是提高运算能力的关键。运算律在小学数学中基本存在于加减乘除之间，而教学现状表明学生对运算律的理解并不到位，以致出现记忆混乱、计算出错等现象。了解不同级别运算间的差别有助于师生更深刻地理解运算律及运算法则中的算理，进而更清晰地识记运算律。

一、从定义及发展看区别（是否针对相同因子）

我们来分析加减乘除的定义。

加法定义：“有限集合A的基数为自然数a，有限集合B的基数为自然数b，且A∩B=Ø，集合A与B的并集的基数为c，那么c叫作a与b的和，记作a+b=c。”[1]加法在小学中的解释是将多个数合并在一起的数学运算。

在小学数学中，我们这样定义乘法，即求几个相同加数的和的简便运算。例如：2+2+2+2+2+2=2×6=12。由定义可知，乘法也是求和运算，即加法运算（这里的定义不适用于一个数乘分数）,只是在加法运算的基础上强调“简便”。也正是由于“简便”一词的限制，乘法只能对相同的数求和，而加法的运算对象范围则更广。

减法定义：“有两个集合A、B，且满足B⊆A，其中集合A的基数为自然数a，集合B的基数为自然数b，集合A、B的差集的基数定义为a-b。”[2]通俗地讲，我们常用加法来定义减法，即已知两个数的和与其中一个数，求另一个数的运算叫作减法。

小学数学中通常有两种方式定义除法。其一，用乘法来定义除法，即已知两个数的积和其中一个因数，求另一个因数的运算叫作除法。其二，在前一种定义成立的基础上，如果乘法可以看作“连加”，则除法可以看作“连减”，即a÷b=c可以理解为a-b-b-b-…-b-b=0（其中共c个b）。事实上，小学数学中通常采用第二种定义方法。

如果将除法定义为“连减”，则其减数永远是相同的数，而减法的减数则可以互不相同，也就是说除法做“连减”考虑时运算对象的范围更小。

二、从运算律看区别（分配律）

?

上表中有(a+b)×c＝a×c+b×c，也就是括号外面的c被分配到括号里面和两个加数分别相乘，我们称之为乘法对加法的分配律。减去一个数等于加上这个数的相反数，由此我们可以推出(a-b)×c＝a×c-b×c，即乘法对减法也具有分配性质。另外，除以一个数等于乘这个数的倒数，由此我们又可以推出(a+b)÷c＝a÷c+b÷c、(a-b)÷c＝a÷c-b÷c，它们分别被称为除法对加法的分配律、除法对减法的分配律。[3]

因此从运算律来看，我们把分配律作为区分运算级别的重要标志。因为加减法这同一级别的运算中不存在对自己或对彼此的分配性质，而乘法对加法可以分配、对减法也可以分配。同样，除法对加法和减法也具有分配性质。换言之，第二级运算（乘法和除法）对第一级运算（加法和减法）具有分配性质。[4]

对此，可以利用第二级和第三级运算（乘方和开方）再次验证这一结论。在乘方中，有：

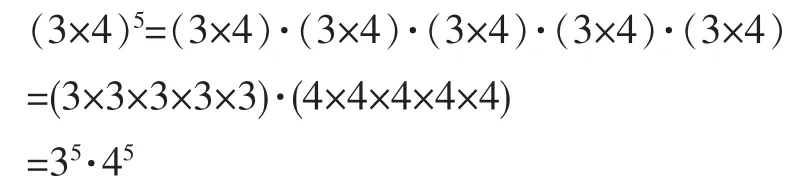
类似的有（ab）n＝an·bn，也就是乘方对乘法有分配律。[5]同样，乘方对除法也有分配律。

上面的过程说明了第三级运算对第二级运算具有分配性质，加之前文提到第二级运算对第一级运算具有分配性质的这一现象，我们说分配律是区分运算级别的重要标志。但需要说明的是，第三级运算对第一级运算不存在这种性质，比如我们都了解（a+b）2＝a2+b2是不正确的。[6]

三、从运算结果看区别（是否产生新量）

1厘米+1厘米=2厘米、1平方厘米+2平方厘米=3平方厘米、5立方米＞3立方米……这样的数量运算及比较在小学中是正确且有意义的。由于相同量之间的加减只是在该量领域内的变化，因此比较也就有了意义。但无论是在生活中还是数学中，我们从来不会花费精力去比较2平方厘米和5立方米。因为前一个量属于平面，后一个量属于空间，这样的比较本身就没有意义。[7]同样地，2平方厘米+5立方米这样的计算也永远不会有答案。

我们来看不同的量在乘除法运算中是否同样没有意义。《数学课程标准（2011）》中要求学生掌握的知识有长度（m）×长度（m）＝面积（m2）、长度（m）×长度（m）×长度（m）＝体积（m3）、速度（m/s）×时间（s）＝路程（m）等。通过这些实例，我们可以看出，有些相同的量及不同的量可以进行乘法运算，结果是一个新的量。通过生活背景，我们又可以知道这些公式的逆运算，即面积（m2）÷长度（m）＝长度（m）、路程（m）÷速度（m/s）=时间（s）等也都是有意义的。因此可以得出结论，除法运算也会产生新的量。

当然，对于数学中的数来讲，因为没有量的限定，所有的数都可以进行加减乘除运算，比如3+2、3-2、3×2、3÷2都是正确且有意义的。但是对于其他科学而言却不得不考虑量的限制。比如物理学的研究对象是温度、长度、质量、时间等量。

综上，乘除的对象可以是相同的量，也可以是不相同的量，重要的是乘除是产生新量的运算，然而加减不是。加减只能在相同的量之间进行运算，得到的结果也是相同领域的量。

四、从运算顺序看区别

在小学四则运算的教学过程中，有学生会提出这样的问题：“为什么要先算乘除，后算加减呢？”[8]“若这是规定，又为什么不规定先算加减，后算乘除？”对于这类问题，我们查阅诸多文献发现，与其说数学有这样的规定，不如说生活有这样的规定。下面来举例说明。

例生活中我们粉刷房子，墙壁和屋顶一般用不同颜色的材料。已知墙壁的面积为84平方米，屋顶的面积为48平方米，而墙壁每平方米所用材料的价格是5元，屋顶每平方米所用材料的价格是4元。粉刷这个房子一共需要多少钱？

对于这样的问题，无论是成人还是小学生，解决问题的第一步一定是分别计算出粉刷墙壁需要的钱和粉刷屋顶需要的钱，再进行相加求一共的费用。列算式为：84×5＝420（元）、48×4＝192（元），420+192＝612（元）。体现在综合算式中也应当是先计算各自的费用再进行求和，即84×5+48×4＝420+192＝612（元）。

生活当中大多数案例的解决都需要先利用乘除计算局部，再利用加减进行综合。虽说数学是抽象的，但其起源依然是生活。换言之，正是因为生活有了这样的“要求”，数学才有了这样的规定。当然，我们也会遇到一些需要先加减、后乘除的问题，这种情况下就产生了括号。

以上四点就是加减与乘除的区别。深入挖掘知识就是深化思维加工的过程，教师和学生理清加减乘除的脉络将会加深对该领域知识的理解，从而做到对数学知识的融会贯通。