一道中考模拟题的解题分析

☉山东聊城市第六中学 扈保洪

一、问题呈现

题目：（2014·宁波一模）如图1，正六边形ABCDEF的边长为4，两顶点A、B分别在x轴和y轴上运动，则顶点D到原点O的距离的最大值和最小值的乘积为______.

答案：当O、D、AB的中点K共线时，OD有最大值和最小值.

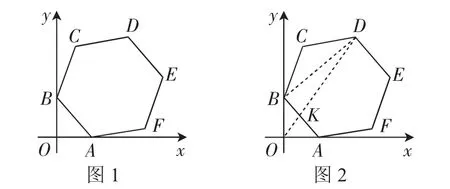
同理，当O、D、AB的中点K共线时，将六边形绕AB的中点K旋转180°取得最小值22.

则顶点D到原点O的距离的最大值和最小值的乘积为48.

在一次辅导中，一名学生拿着他从网上下载的上述试题及其答案，问：为什么说，当O、D及AB的中点K共线（参见图2）时，OD有最大值和最小值？于是解题分析即由此展开.

二、分析遇阻

显然，根据三点不等式，即可解释学生提出的上述问题.但在上述解答中，通过对OD取最大值的位置进行旋转来求其最小值的方法是错误的.这是因为，当点O、D及AB的中点K共线（见图2）时，将正六边形ABCDEF绕AB边的中点K旋转180°后，使得点A、B均离开了原来所在的坐标轴，这既与已知条件矛盾，又有主观臆造之嫌.所以，这个错误自然引发了笔者对OD取最大值与最小值时其位置关系的思考，而这也是正确解答上述题目的关键所在.

但是，进一步分析发现：当点A、B分别在x轴、y轴上移动时，对于AB边的中点K来说，由于OK=知，其运动轨迹应是以原点O为圆心、以为半径的⊙O；与此同时，正六边形ABCDEF还做着以点K为中心的旋转运动.因此，正六边形ABCDEF的运动实际上是包含上述两个旋转的复合运动.而这种复合的旋转运动又较为复杂，要想通过直接考察正六边形ABCDEF的运动来弄清上述问题，进而判定OD在何处取最大值、在何处取最小值，显然是困难的.

三、转换思路

先给出一个引理：如图3，P是⊙O外一点，直线PO分别交⊙O于A、B两点，则PA是点P到⊙O的极小距离，PB是点P到⊙O的极大距离.

证明：如图3，在⊙O上任取一点Q，连接PQ、OQ.显然，由三点不等式知PB=PO+OB=PO+OQ≥PQ≥PO-OQ=PO-OA=PA.因此，PA的长是极小值，PB的长是极大值.

再回到图1中，当点A、B分别在x轴、y轴上移动时，无论正六边形ABCDEF在坐标系xOy中怎样运动，它与坐标系xOy的位置关系总具有相对性.因此，既然正六边形ABCDEF所做的复合运动，其规律性不便于把握，那么不妨反过来思考，把正六边形ABCDEF固定起来，而使坐标系的x轴、y轴分别经过定点A、B进行滑动.这样一来，因为在Rt△AOB中，总有中线OK=，所以原点O移动的轨迹应是以AB为直径的⊙K.于是由引理知，OD所取的极大值与极小值，可分别视为定点D到⊙K距离的极大值与极小值，从而⊙K与直线DK的两个交点应分别是OD取极大值与极小值时原点O所在的位置.此外，值得注意的是，x轴、y轴分别经过定点A、B所做的推拉运动，既使原点O沿⊙K转动，又使坐标系xOy绕原点O旋转.

因此，当OD取极大值与极小值时，根据原点O所在的不同位置，以及两坐标轴绕原点O旋转后的方向，可将其搭配成下列四种情况，分别如图4、图5、图6、图7所示，这些情况的先后顺序可视为：图4（先把图4中坐标系xOy旋转到图4中坐标系xO1y的位置）→图6（图6中坐标系xOy由图4中坐标系xO1y旋转得到，而图6中坐标系xO1y表示的是图4中坐标系xO1y所在的位置；下列相邻两图之间坐标系的位置可以此类推，不再重复说明）→图7→图5→图4，且各图中线段OD的长即为OD的极大值，线段O1D的长即为OD的极小值.

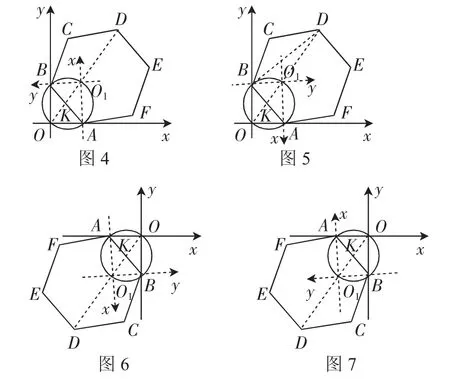
根据上述引理，在图4至图7中，每种情况下OD所取的极大值（或极小值）均相同，故解题时只需任选其中的一个图示即可（不妨以图5为例）.

连接BD，显然△BDK为直角三角形（因∠DBK=∠CBA-∠CBD=120°-30°=90°），且易知BD=4，BK=2，DK=，故OD的最大值为22，最小值为22，所求的乘积为48.

那么，如果重新回到把坐标系xOy的位置固定，而使正六边形ABCDEF的两顶点A、B分别在x轴和y轴上运动的状态，上述问题又该怎样解呢？

四、图示解读

在图4至图7中，因均有AB=OO1，且AB与OO1互相平分，故这几个图中的四边形AOBO1都是矩形.于是，对每一个图来说，从OD取极大值的位置到取极小值的位置，需先把坐标系的原点O沿⊙K转动一个半圆弧到点O1，再使两条坐标轴以新原点O1为旋转中心，按逆时针（或顺时针）方向旋转90°即可；另一方面，由矩形AOBO1的两组对边分别相等，知当OD取极大值时，点A、B各自到原点O的距离分别等于OD取极小值时点B、A到原点O1的距离.

基于上述分析，如果重新回到把坐标系xOy的位置固定，而使正六边形ABCDEF的两顶点A、B分别在x轴和y轴上运动的状态，那么根据正六边形ABCDEF与两个坐标系的相对位置关系，则可把图4、图5、图6、图7依次改为图8、图9、图10、图11，其旋转变换的先后顺序相应的依次为：图8→图10→图11→图9→图8.

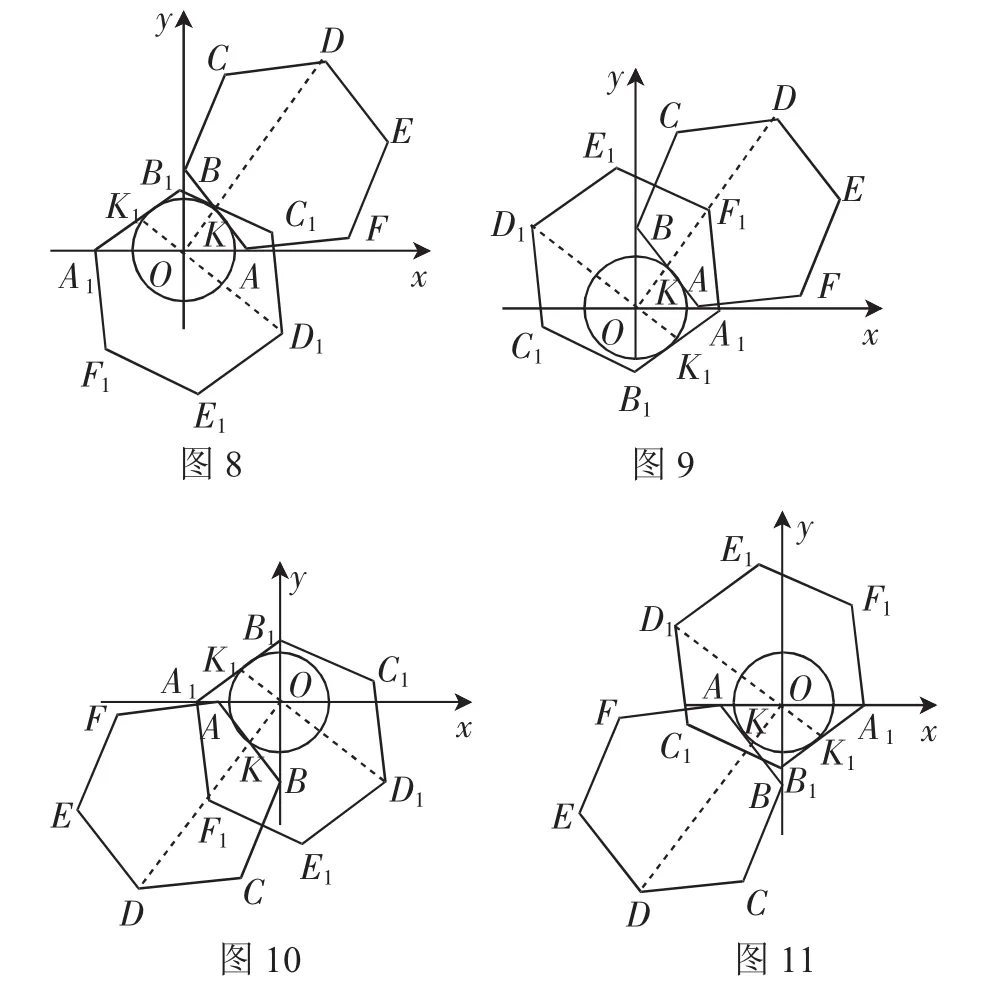
这样，有了图8至图11以后，在正六边形ABCDEF做复合转动的状态下，就可以对OD取极大值与极小值的位置关系做出精准分析.不妨以图8为例，易知△AOB≌△BOA，OK=OK=B，AB⊥AB（∠BAO+∠BAO=∠BAO+∠ABO=90°），OD⊥K1D1（∠KOK1=∠KOB+∠K1OB1=∠KBO+∠K1B1O=∠KBO+∠KAO=90°），且点K沿⊙O转动等.于是，要使正六边形ABCDEF从OD取极大值的位置运动到OD取极小值的位置，则可采用下列方法（参见图8）：

把点A沿x轴向左移动到点A1的位置，且使OA1=OB，与此同时，在点A的带动下，点B沿y轴相应移动到点B1的位置，根据勾股定理，显然OB1=OA，再根据正六边形ABCDEF的运动方向，画出相应的正六边形A1B1C1D1E1F1即可，此时OD1的长就是所求的极小值.同理，对于图9至图11来说，其情况均与此类似，不再赘述.

若把图8至图11的情况综合起来，则表明：当正六边形ABCDEF的两个顶点A、B分别在x轴、y轴上移动时，使OD取极大值的点有两个，分别在一、三象限内，且它们与原点O共线；而使OD取极小值的点也有两个，分别在二、四象限内，它们也与原点O共线，且该直线与两个极大值点所在的直线互相垂直.

根据以上分析，可把本文开头所呈现的解答过程修正为：

在图1中，分别连接OK（点K是AB边的中点）、DK、OD.当正六边形ABCDEF转动时，只有在△ODK的三条边共线的情况下才能使OD取极值，这样的情况共有图8至图11所示的四种.而由三点不等式，知此时均有DK+OK≥OD≥DK-OK=OD1，故这四种情况下，OD所取的极大值（或极小值）相同，从而其极大（小）值即为最大（小）值.不妨以图9为例，易知OK=2、DK=2均为定值，所以OD的最大值为2+2，最小值为2-2，它们的乘积为48.

五、解题感悟

通过以上的解题分析，笔者有以下几点感悟：

（1）对于动态型几何问题来说，解答时应遵循“动静结合，动中求静、以静制动”的基本思路.而在“动中求静”阶段，应通过审题，弄清图中运动的部分是如何动的，其路径是怎样的，然后通过模拟演示，对整个运动的过程进行分段考察，以找到比较关键的位置有哪些，并把这些关键位置分别用静态图形表示出来；在“以静制动”阶段，则可借助所画出的各个静态图形，以它们为思维“节点”探究解题思路，并结合题中所给的信息，综合运用所学知识灵活解决问题.

（2）当解题遇到困惑时，应引导学生换一个角度思考问题，或以退求进，或正难则反，或类比联想，或等价转换，这样才能使数学探究活动既卓有成效又丰富多彩.比如，在上述问题中，根据正六边形ABCDEF的运动，直接探索OD取最大值与最小值的位置关系受阻时，转换一种角度思考，把正六边形ABCDEF的位置固定，而让坐标系xOy动起来，待找到方法后，再类比联想，则很快突破了原本难以画图的阻滞点，使问题迎刃而解.

（3）解题分析不能只靠简单想象.应使学生养成动手操作、实验探究的习惯，特别是要善于画图分析，从直观上进行观察、猜想、尝试、验证、推理、交流等活动，让动手操作与动脑思考达到和谐统一，这样有利于学生准确领会与把握问题的深层结构，更好地理清思路、开拓创新，从而迅速找到解决问题的有效途径.比如，在上述问题中，若先制作一个正六边形的纸板，再利用它来演示正六边形ABCDEF的复合运动，则对于发现其运动的规律性，进而探索出该题的解法大有裨益.

1.扈保洪.一道填空题引发的思考［J］.中学数学（下），2015（4）.W