构造直角三角形解题例谈

☉《中学生学习报》社有限公司 姜红伟

直角三角形是一类最基本而特殊的几何图形，有许多重要的性质，为我们解决一般三角形、四边形的问题作了知识铺垫.于是，通过作高、构造直角三角形、利用直角三角形的性质解决更一般的几何图形中的证明或计算问题，就是一条大行其道的解题大法，尤其在初高中数学衔接地带很有作用.

一、直角三角形的性质

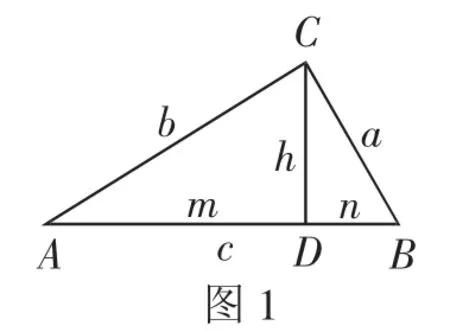
如图1，Rt△ABC中，C=90°，角A、B、C所对的边分别为a、b、c，CD⊥AB于D.设CD=h，AD=m，BD=n.则：

（1）斜边AB上的中线等于AB的一半.

（2）30°角所对的直角边等于斜边的一半.

（3）两锐角互余，A+B=90°.

（4）勾股定理，a2+b2=c2，a＜c，b＜c.

（5）射影定理，h2=mn，a2=nc，b2=mc.

（6）边角关系，a=csinA，或a=btanA，或b=ccosA.

二、构造直角三角形

解答某些一般几何图形中的计算或证明问题时，可添加适当的辅助线把它们分割成一些直角三角形，从而转化成可以运用解直角三角形的有关知识解决这些图形中求边角的问题.注意：由于解直角三角形是数形结合的重要内容，所以在分析问题时，可尽量画出相关的平面示意图帮助思考.

三、典型例题解析

例1 如图2，在△ABC中，∠C=150°，AC=4，tan

（1）求BC的长；

（2）利用此图形求tan15°的值（精确到0.1，参考数据：=1.4，=1.7，=2.2）.

解析：（1）注意到∠C=150°，所以其补角为30°（非常特殊的角），故过A作AD垂直BC所在的直线于D，则在Rt△ACD中，AD=AC=2，进而CD=在Rt△ABD中，tanB=，代入值即得BC=16-2

（2）在CB上取一点E，使得CE=AC，则∠AEC=15°.

例2 如图3，在正方形ABCD外作等腰直角△CDE，DE=CE，连接BE，求tan∠EBC.

解析：作EF⊥BC于F，设DE=CE=a.

所以∠ECF=45°，所以△CEF为等腰直角三角形，则CF=EF=

例3 如图4，天星山山脚下西端A处与东端B处相距800（1+米，小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°，东端的坡角是30°，小军的行走速度为米/秒.若小明与小军同时到达山顶C处，则小明的行走速度是多少？

解析：过点C作CD⊥AB于点D，设AD=x米，小明的行走速度是a米/秒.

由∠A=45°，CD⊥AB，得AD=CD=x米，则AC=x米.

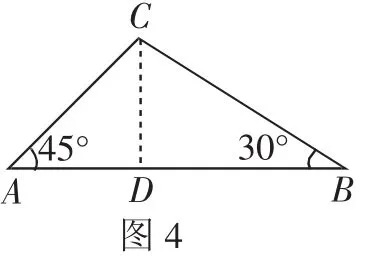
答：小明的行走速度是1米/秒.

例4 在△ABC中，已知AB=2，AC=3，∠A=60°.

（1）求BC的长；

（2）求sin2C的值.

解析：如图5所示.

（1）过B作BD⊥AC于D，则在Rt△ABD中，由∠A=60°，AB=2，得∠ABD=30°，AD=1，BD=

（2）延长BD至E，使DE=BD，连接CE，则∠BCE=2∠BCA.

解析：画出符合条件的示意图，如图6.

延长BA，过C作CE⊥BA于E.

在△ABD中，BD=AD，则过D作DF⊥AB于F后，有AF=BF=3，进而AD=BD=

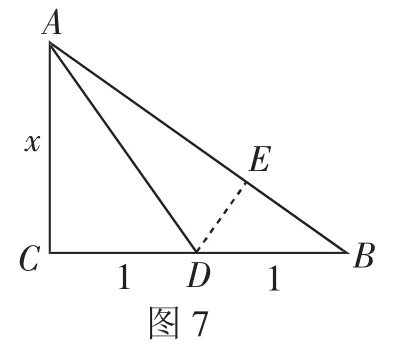
例6 如图7，△ABC中，∠C=90°，D是BC的中点，若sin∠BAD=，求sin∠BAC的值.

解析：试题已知具有丰富的数形结合要素，特别是sin∠BAD=给人以广阔的联想、转化空间（初中阶段必须构造直角三角形），待求式却十分简捷、明了.

为了简化运算，不妨设CD=DB=1，AC=x，x＞0.

过D作DE⊥AB于E，则AB2=x2+4，AD2=x2+1.

例7 如图8，在四边形ABCD中，∠B=135°，∠C=120°，AB=2，BC=4-2，CD=4，求AD边的长.

解析：过点A、D分别作AE、DF垂直于直线BC，垂足依次为E、F.

过点A作AG⊥DF，垂足为G.在Rt△ADG中，根据勾股定理得AD2=EF2+（DF-AE）2=（4+）2+（=（2+2，所以AD=2+2

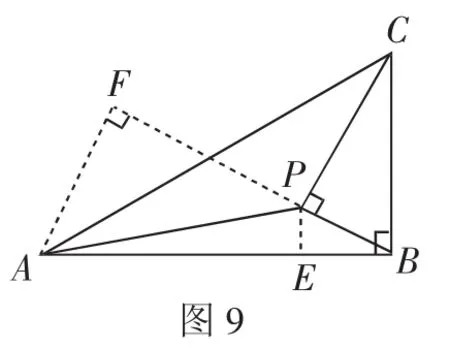
（2）若∠APB=150°，求tan∠PBA.

解析：过P作PE⊥AB于E.

（2）过A作AF⊥BP所在的直线，F为垂足，则∠APF=30°.设AF=a，则AP=2a，PF=

由已知可得Rt△PBC∽Rt△FAB，

从而在Rt△ABF中，

综上所述，作高、构造直角三角形是一种重要技能.只需要用到直角三角形的边角关系，勾股定理，三角形三内角和定理和面积公式等，但思想方法是中学阶段学生必学、必会的等价转化思想、数形结合思想，它是将一般三角形（往往含有30°、45°、60°、75°、120°、135°、150°等特殊角）中求边、角、面积、三角比等问题转化为直角三角形中的问题，进行解决.W