阻力伞锁滚柱梁冲击失效分析

刘继军， 郭 军， 刘小川， 周俊明

(1.中国飞机强度研究所 结构冲击动力学航空科技重点实验室，西安 710065； 2.中航工业航宇救生装备有限责任公司 空降空投研发部，湖北 襄阳 441003)

阻力伞作用是缩短飞机着陆滑跑距离。面积达几十平米的阻力伞产生的巨大阻力可大幅缩短飞机着陆滑跑距离，从而保证在应急情况下飞机不会冲出跑道。阻力伞锁连接机身尾部和阻力伞，是关系阻力伞能否正常开伞的关键机构。阻力伞锁滚柱梁失效会引起飞机阻力伞未完全开伞而抛伞的严重故障。因此，开展阻力伞锁滚柱梁失效机理和失效分析方法研究具有重要意义。

国内外针对阻力伞进行了较为充分的研究，相关内容包括开伞试验方法及过程[1-2]、开伞伞衣载荷特性[3]、开伞过程的流场特性[4-5]等。但针对阻力伞锁研究较少，仅见文献[6-7]对阻力伞锁的相关疲劳试验及机构设计进行过讨论，尚未见有对阻力伞锁滚柱梁失效的相关分析。

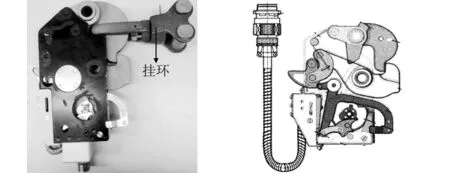
图1 阻力伞锁 图2 阻力伞锁运动机构Fig.1 Parachute lock Fig.2 Motion mechanism

当滚柱梁受到的初始冲击速度载荷过大，就会发生剪切失效，如图3和图4所示。滚柱梁失效过程模型化为两端固支的圆截面梁在均匀冲击载荷(或冲击速度[8])作用下剪切失效过程。

图3 滚柱梁图 图4 滚柱梁失效 Fig.3 Roller beam Fig.4 Roller beam failure

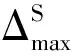
本文先对典型阻力伞锁运动机构进行动力学分析，以确定滚柱梁冲击载荷或初始冲击速度；然后，将滚柱梁的剪切失效过程模型化为均匀冲击载荷下两端固支的圆截面梁动态失效问题；最后，基于分析结果开展典型阻力伞锁滚柱梁失效故障机理分析。

1 阻力伞锁滚柱梁载荷分析

阻力伞开伞伞绳拉直瞬间给阻力伞锁机构一个冲击波或冲量I0，该冲量使得静止状态的阻力伞锁运动机构在极短时间tc(毫秒级)内达到某个运动状态，则滚柱梁受到一个初始冲击速度υ0。图5为典型的阻力伞锁运动机构，主要由挂环、受力钩、支承钩、耳片、曲臂、滚柱梁及套筒组成，是“旋转杠杆/省力增速”的机构。

由于阻力伞锁运动机构受到的冲击载荷作用时间极短，各部件的位移和转角为小量，可近似认为各部件几何位置关系保持不变。在冲量I0作用后，挂环速度为υ1，沿着Y方向；受力钩绕轴A的角速度为ω1；支承钩绕轴B的角速度为ω2；耳片绕瞬心轴O的角速度为ω3；曲臂绕轴F的角速度为ω4；滚柱梁及套筒速度为υ0，垂直于GF方向。忽略运动机构的摩擦力和摩擦力矩，应用动量定理和动量矩定理,推导在冲量I0作用后滚柱梁及套筒的初始冲击速度。

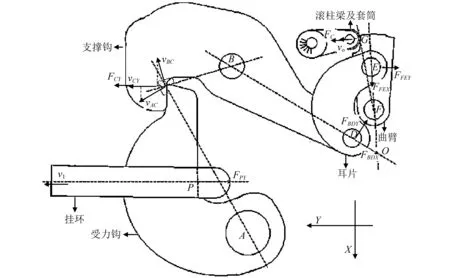
图5 阻力伞锁机构运动关系Fig.5 Dynamics of the motion mechanism

令挂环质量为m1，受力钩与其作用力为FPY，则

(1)

令受力钩转动惯量为J1，支撑钩与其作用力为FCY，绕轴A

从上述评定结果可以看出，该煤矿的绿色矿山建设评价是合格的，在6项绿色矿山建设评价指标中，除环境重建指标为较差外，其他5项指标均为合格。根据评价结果，矿山开采企业在后期的运营中应更加注意环境指标的建设，同时应提高开采技术，提高开采效率，减轻环境污染，提高矿山的绿色化程度。

(2)

令支撑钩转动惯量为J2，耳片与其作用力为FBDX、FBDY，绕轴B

(3)

令耳片转动惯量为J3，支撑钩与其作用力为FFEX、FFEY，绕瞬心轴O

(4)

令曲臂转动惯量为J4，滚柱及套筒与其作用力为FG，绕轴F

(5)

令滚柱梁质量为m0，套筒质量为ηm0，则

(6)

且机构运动存在如下运动关系

ω1·XACX=ω2·XBCX

(7)

ω2·LBD=ω3·LOD

(8)

ω3·LOE=ω4·LFE

(9)

υ1=ω1·XAP

(10)

υ0=ω4·LFG

(11)

联立式(1)～式(11)，可得

(12)

其中,

(13)

表1和表2为某阻力伞锁运动机构参数，代入式(12)和式(13)，可得α=3.970 5 kg，β=0.002 7 kg，可见滚柱梁及套筒的初始冲击速度υ0与输入冲量I0成线性关系，阻力伞锁运动机构的等效质量meq=4.0 kg。

图6为典型阻力伞锁运动机构可能受到的冲量随时间变化图，由图可知最大可能冲量为I0=741.5 N·s，则对应的滚柱梁及套筒受到的初始冲击速度：υ0=185.9 m/s。

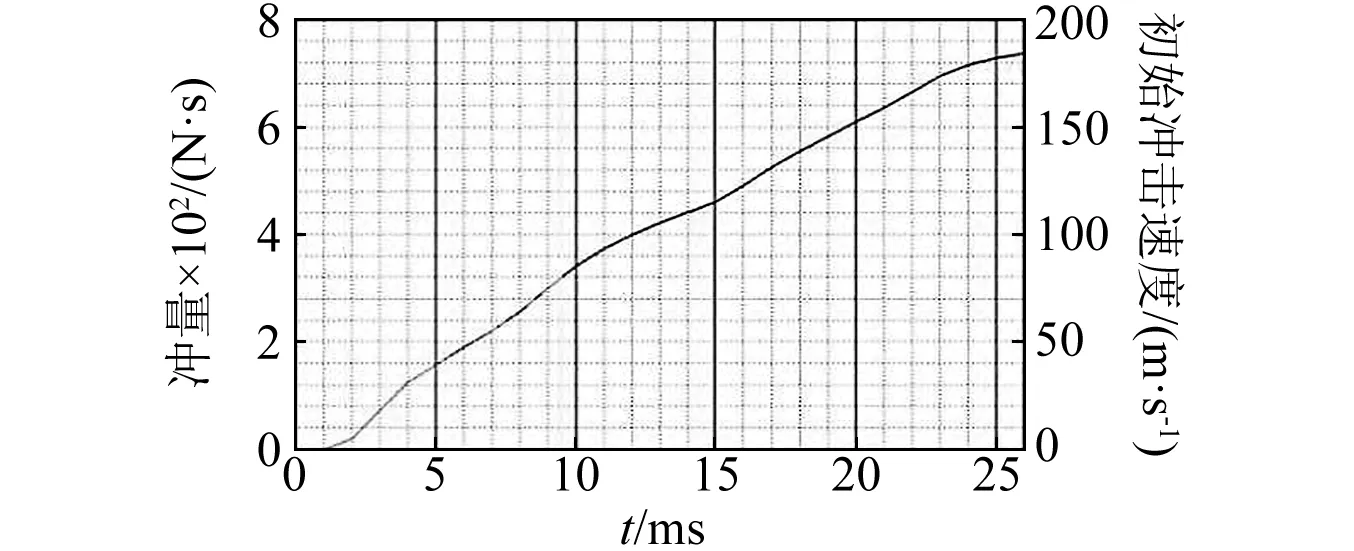
图6 冲量和初始冲击速度关系图Fig.6 Impulse and initial velocity

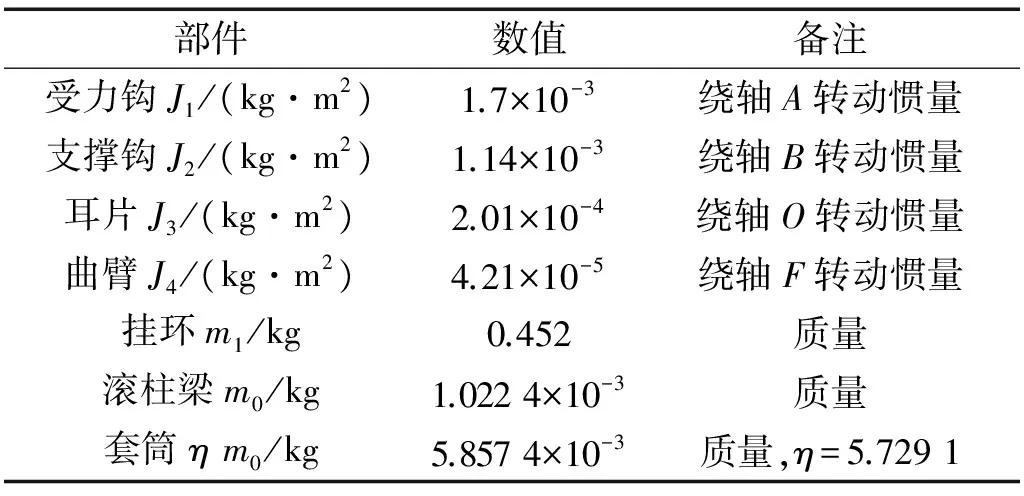
部件数值备注受力钩J1/(kg·m2)1．7×10-3绕轴A转动惯量支撑钩J2/(kg·m2)1．14×10-3绕轴B转动惯量耳片J3/(kg·m2)2．01×10-4绕轴O转动惯量曲臂J4/(kg·m2)4．21×10-5绕轴F转动惯量挂环m1/kg0．452质量滚柱梁m0/kg1．0224×10-3质量套筒ηm0/kg5．8574×10-3质量，η=5．7291

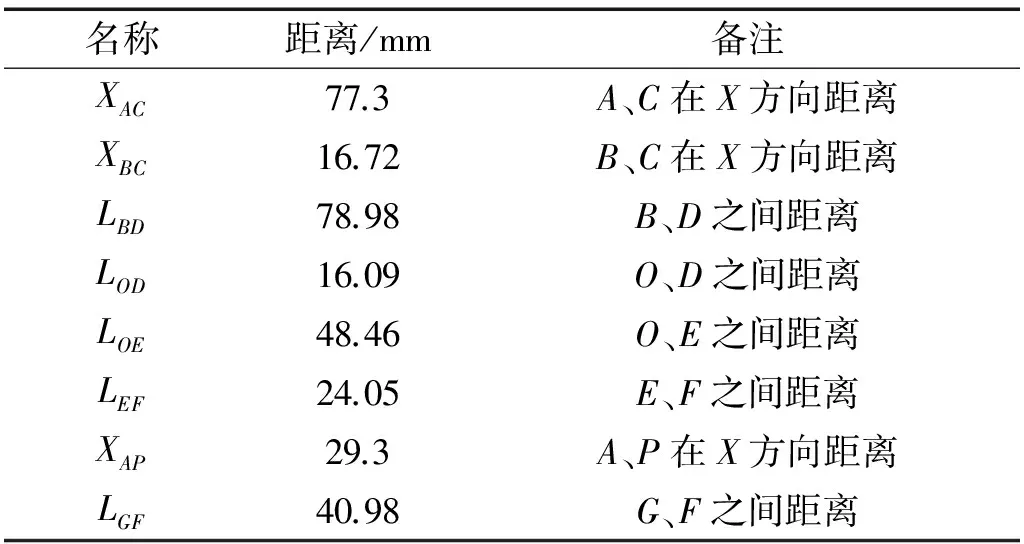
表2 典型阻力伞锁运动机构各部件位置关系参数

2 阻力伞锁滚柱梁冲击失效分析

两端固支的滚柱梁受到均布初始冲击速度υ0作用，考虑失效模式Ⅲ，支点A处梁截面保持在剪切力Q0作用下，令其剪切滑移变形量为ΔS，剪切滑移变形速度为υS，而在梁内部移行铰B处速度仍为υ0，该处剪切力为0，整个滚柱梁在支点滑移下的速度场见图7和图8。

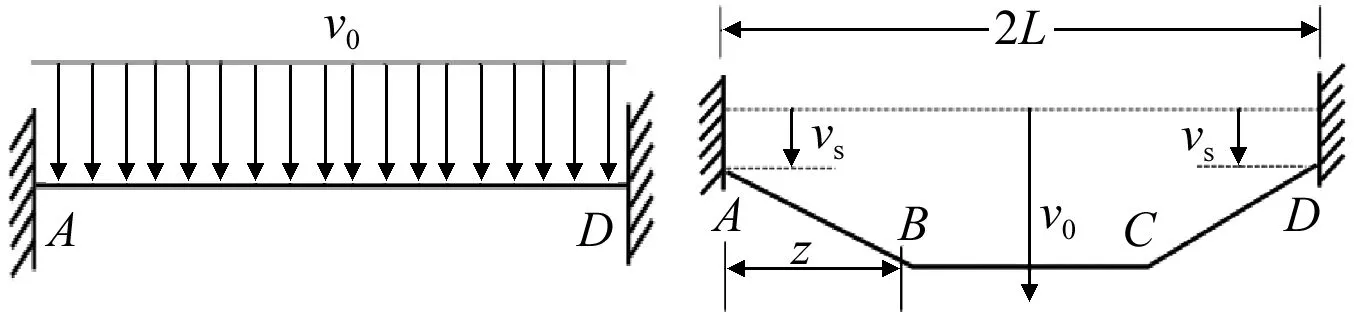
图7 初始冲击速度场图8 支点剪切滑移下的速度场 Fig.7 Initial velocity field Fig.8 Velocity field of shear slip

根据材料的刚塑性假设，两铰之间AB段为刚性的，两端受到弯矩为塑形极限弯矩M0，取其为研究对象，见图9，令滚柱梁密度为ρ，截面积为S，移行铰B～支点铰A距离为z，质心(该段梁中心)处速度为υ，由动量定理，得

(14)

AB段绕A转动，由动量矩定理，得

(15)

时刻t支点滑移变形速度为υS，式(14)、式(15)分别积分可得

(16)

(17)

可见，在υS=0之前，z=6M0/Q0是定值，即移行铰B和C也是位置不变的塑性铰。当时υS=0时

(18)

则根据失效模式Ⅲ及初等失效准则，则应满足

(19)

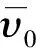
(20)

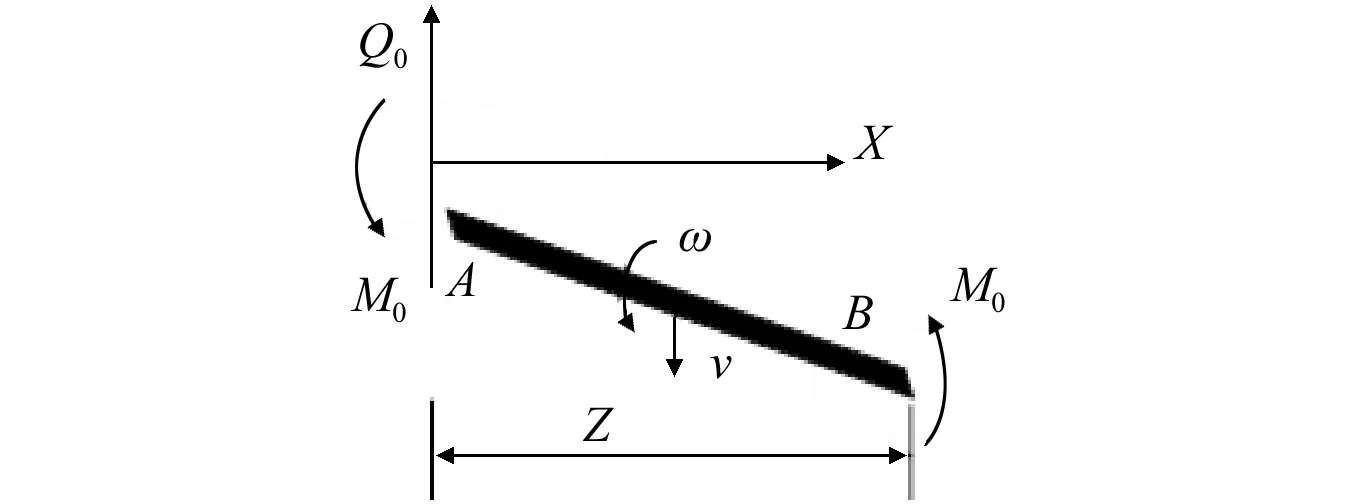
图9 刚体段Fig.9 Rigid bar

(21)

代入式(20)，得

(22)

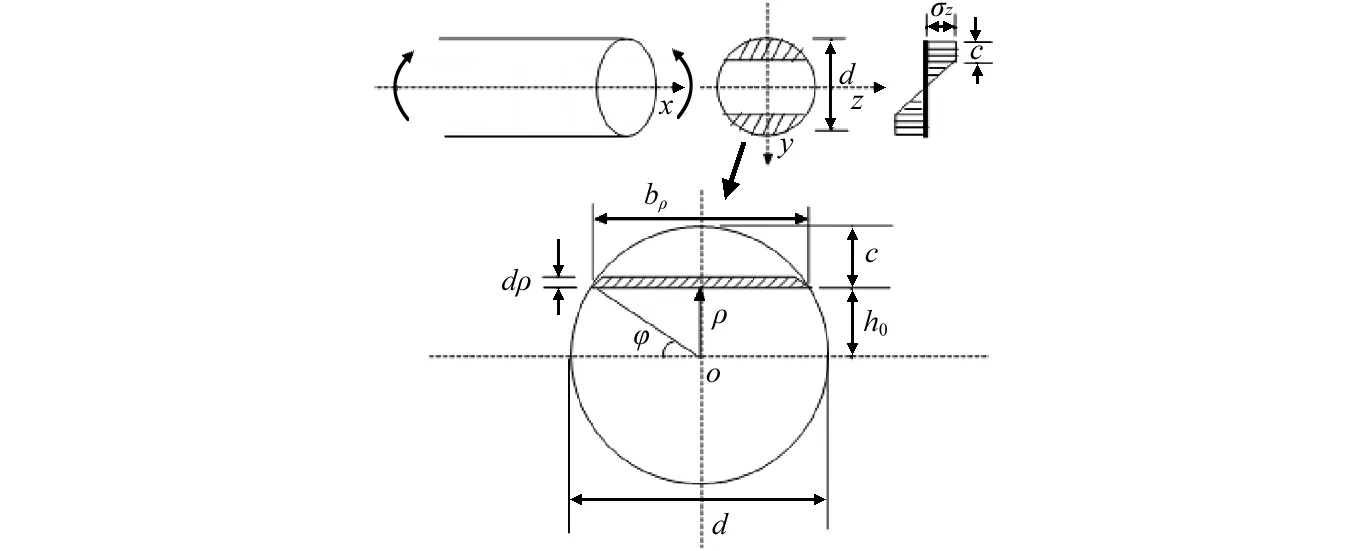
图10 滚柱梁横截面应力分布Fig.10 Stress of cross-section of roller beam

系数λc=kπ/3为圆截面梁的Johnson损伤数临界值，是常数。梁剪切失效的临界失效冲击速度仅与材料参数有关(屈服强度和密度)，而与梁横截面几何参数无关，也是材料特性参数。该结论表明不同直径梁有同样临界失效冲击速度，这与直观结论相悖。可以从以下两方面解释：①梁受到速度冲击载荷即梁每个质点都具有初始速度，即意味着不同截面尺寸的梁剪切失效所需要的冲量大小不同；②梁横截面几何参数如直径虽不会影响临界失效冲击速度，但若输入冲量为定值时，则梁的初始冲击速度会随直径增加而减小，从而会影响梁失效行为。

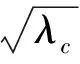
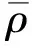
(23)

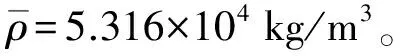
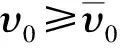
3 套筒与滚柱梁质量比η对滚柱梁的失效影响

从式(14)和式(15)可见，套筒惯性对滚柱梁失效有影响，但并不影响滚柱梁横截面的刚度特性、极限剪切力和塑形极限弯矩，所以用等效密度的工程化处理方法来考虑套筒对滚柱梁段的惯性影响是合理的。

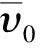
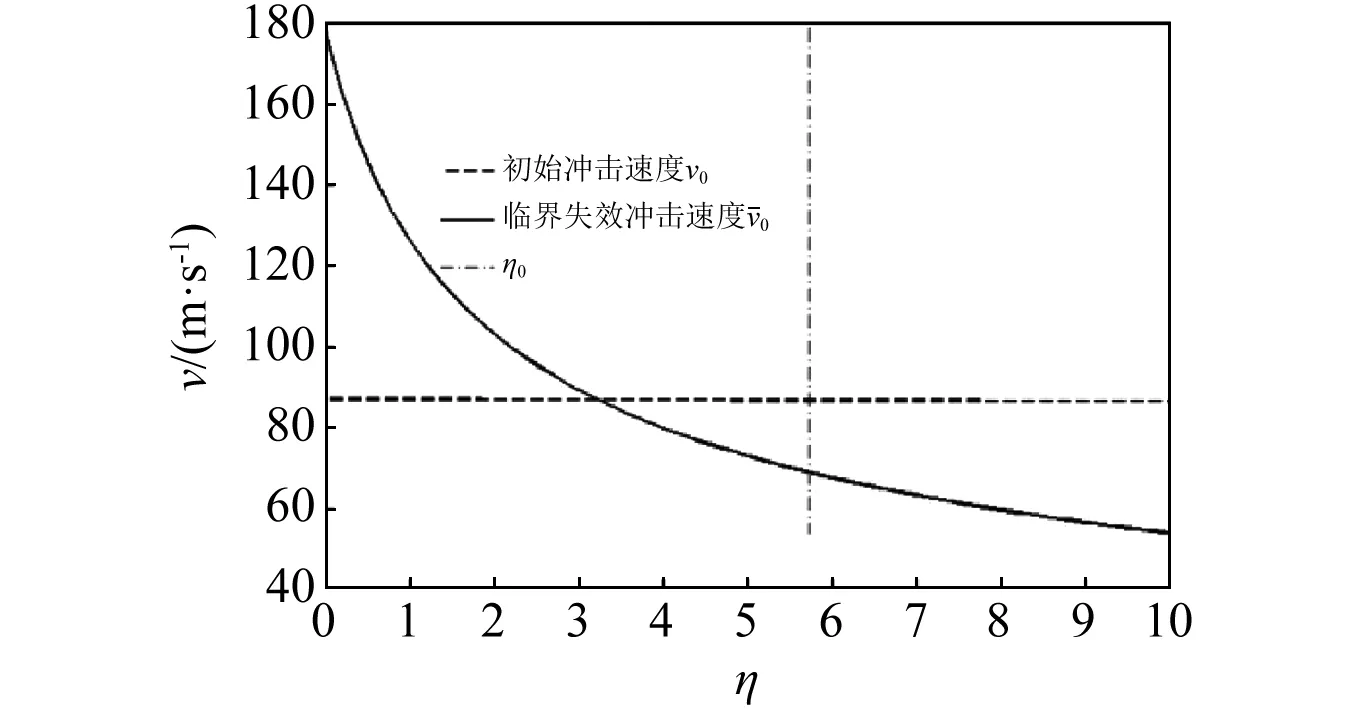
图11 速度与η的变化关系Fig.11 Velocity vs η

4 结 论

本文认为阻力伞开伞伞绳拉直瞬间对阻力伞锁运动机构施加一个初始冲量，该冲量是滚柱梁失效根本原因。通过对典型阻力伞锁运动机构动力学建模和滚柱梁失效机理分析，得到滚柱梁初始冲击速度和临界失效冲击速度与输入冲量的函数关系。针对某型阻力伞锁分析和计算表明，该伞锁滚柱梁的初始冲击速度大于临界失效冲击速度，成功解释了滚柱梁失效机理和试验故障原因。

套筒惯性对滚柱梁初始冲击速度和临界失效冲击速度都有影响。但套筒与滚柱梁质量比对滚柱梁初始冲击速度影响可忽略不计，但对滚柱梁临界失效冲击速度有较大影响；降低η值，可以提高临界失效冲击速度。

不考虑剪切滑移面厚度变化引起的塑形极限剪切力和弯矩弱化，即式(20)计算的圆截面滚柱梁临界失效冲击速度偏保守，有利于滚柱梁的动强度设计。

从阻力伞锁滚柱梁设计角度看，仅采用传统的静强度设计方法不能满足滚柱梁的设计要求，必须充分考虑冲击载荷进行动强度设计。

[ 1 ] 余莉，明晓，胡斌. 降落伞开伞过程的试验研究[J]. 南京航空航天大学学报，2006,38(2)：176-180.

YU Li, MING Xiao, HU Bin. Experimental investigation in parachute opening process[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006,38(2)：176-180.

[ 2 ] 王从磊，孙建红，喻东明. 阻力伞拉直过程的影响因素分析[J]. 南京航空航天大学学报，2013,45(2)：196-201.

WANG Conglei, SUN Jianhong, YU Dongming. Analysis of effect factors on deployment of drag parachute[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013,45(2)：196-201.

[ 3 ] 余莉，张鑫华，李水生. 降落伞伞衣载荷的性能试验[J]. 北京航空航天大学学报，2007,33(10)：1178-1181.

YU Li, ZHANG Xinhua, LI Shuisheng. Experimental on canopy payload performance parachute[J]. Journal of Beijing University of Aeronautics & Astronautics, 2007,33(10)：1178-1181.

[ 4 ] 完颜振海，冯顺山，董永香，等. 超音速伞弹流场特性数值分析[J]. 兵工学报，2011,32(5)：520-525.

WANYAN Zhenhai, FENG Shunshan, DONG Yongxiang, et al. Numerical Analysis of flow field characteristics of supersonic submunition with parachute[J]. Acta Armamentarii, 2011,32(5)：520-525.

[ 5 ] TAKIZAWA K, TEZDUYAR T E,BOSWELL C,et al. Special methods for aerodynamic-moment calculations from parachute FSI modelling[J]. Computational Mechanics,2015,55(6):219-226.

[ 6 ] 沈文波，季享文.基于图像视觉作动控制的寿命试验台研制[J]. 计算机测量与控制，2015,23(17):2434-2437.

SHEN Wenbo, JI Xiangwen. Development of life test device based on image visual motion controlling[J]. Computer Measurement & Control, 2015,23(17):2434-2437.

[ 7 ] 苏新兵，王建平，周瑞祥.某型飞机新型阻力伞锁机构改进设计[J]. 液压与气动，2008(2) ：11-13.

SU Xinbing, WANG Jianping, ZHOU Ruixiang. Ameliorated design of new decelerated umbrella furnishment for a certain airplane[J]. Chinese Hydraulics & Penumatics, 2008(2) ：11-13.

[ 8 ] 余同希，邱信明.冲击动力学[M]. 北京：清华大学出版社，2011.

[ 9 ] YU T X, CHEN F L. Failure modes and criteria of plastic structures under intense dynamic loading:a review[J]. Matals and Materials,1998,4(3): 219-226.

[10] MENKES S B, OPAT H J. Broken beams[J]. Experimental Mechanics, 1973,13(11): 480-486.

[11] JONES N. Plastic failure of ductile beams loaded dynamically [J]. Journal of Engineering for Industry，1976，98(1):131-137.

[12] YU T X, CHEN F L. A further study of plastic shear failure of impulsively loaded champed beams[J].International Journal of Impact Engineering, 2000,24(6):613-629.