地震动参数对土坡地震响应的影响权重研究

张江伟， 李小军， 齐剑峰， 王玉石， 贺秋梅

(1.河北地质大学 勘查技术与工程学院，石家庄 050031；2.中国地震局 地球物理研究所，北京 100081)

地震诱发滑坡是一种常见的地震次生地质灾害，在居民集中的山区发生强烈地震后，地震触发的滑坡的危害性往往比地震直接造成的灾害还要大[1]。2008年发生在我国四川省汶川县的Ms8.0级大地震触发了大规模的山体滑坡、崩塌等地质灾害，吞没了大量当地居民的家园，给人类生命、财产安全和社会可持续发展带来了巨大的损害。

研究地震作用下边坡稳定性问题时，由于地震动存在随机性，所以地震动强度指标的选取是首要解决的问题。长久以来，地震动峰值加速度和地震动峰值速度一直被地震工程学家和工程师认为是能够表征地震动潜在破坏势的参数。现有的相关研究已有不少，如文献[2-10]等均采用了地震动峰值加速度作为主要强度指标对边坡动力问题进行了研究分析。王秀英等[11]收集了汶川地震诱发的近3 000个滑坡资料和记录到的地震动数据，对地震诱发滑坡与地震动峰值速度的关系进行了研究分析，发现地震诱发滑坡与地震动峰值速度(Peak Ground Velocity, PGV)存在明显的正相关性，可以利用PGV作为判别地震滑坡的判据；Saygili等[12]利用了地震动峰值加速度(Peak Ground Acceleration,PGA)和地震动峰值速度(PGV)两个参数来预测坡体的滑动位移。我国刘恢先在上世纪为编制中国地震烈度表曾将PGA和PGV分别与烈度进行了相关性分析，结果显示这两个参数都和烈度有很好的相关性。除此之外，也有学者展开地震动持时和频谱特性对边坡动力稳定性影响的研究，如徐光兴等[13]选用不同地震动峰值加速度、持时以及频谱参数，对边坡动力响应的影响规律进行了研究分析，结果表明坡面加速度峰值放大系数随输入地震波振幅、频率的增加而减小，持时对加速度峰值响应的影响不大，坡体位移随振幅、持时的增加而显著增大，随频率的增大而减小。闫坤伐等[14]也对地震动加速度振幅、频谱及持时对边坡动力响应的影响规律做了研究。

纵观目前研究，全面地对地震动各参数影响权重的研究较少，导致在分析边坡地震动力稳定性时，地震动参数的选取尚不统一。基于以上背景，本文选取100条具有不同峰值加速度(PGA)、峰值速度(PGV)、阿里亚斯强度(Arias Intensity,AI)、绝对累积速度(Cumulative Absolute Velocity,CAV)、持时和特征周期的地震动记录，计算并分析了各强度指标与边坡动力响应的相关性，得到各参数的影响权重，为边坡地震动力响应分析提供地震动参数选用的基础和依据。

1 计算方法

1.1 有限元法

在研究分析地震作用下边坡稳定性问题时，有限元数值模拟方法采用实际的地震动输入，真实反映坡体在地震下的动力响应特性，且不受边坡地质条件、几何形态等因素的限制，可以解决难以用解析法求解的问题，更加实际合理地评价地震作用下边坡动力稳定性。因此有限元数值模拟方法在解决边坡地震稳定性问题中得到了广泛而深入地应用。

有限元法是把结构模型离散为有限个单元体，单元体在受到地震荷载作用时，运用考虑单元体惯性和阻尼因素影响的动力力学平衡方程来求解。动力力学平衡方程可表达为式(1)

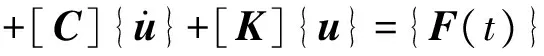
(1)

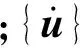
对于求解地震作用下的动力问题，动力荷载就是地震荷载，于是求解边坡地震动力稳定性问题的基本力学运动方程可写为

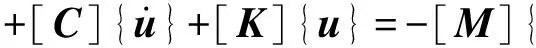
(2)

式中：{üg(t)}为地震动加速度时程。

1.2 相关性计算方法

在边坡地震稳定性评价中，合理的地震动强度指标应能突出反映边坡地震响应的程度。本文通过Pearson相关系数来确定地震动各参数对边坡地震响应的影响权重，从而得到评价边坡地震稳定性的合理参数。Pearson相关系数是英国统计学家皮尔逊于19世纪80年代提出的一种计算两个变量之间相互关系的指标，范围在-1.0～1.0的无量纲指数，用来考察两个事物之间相关程度的强弱。随后在学术研究中被广泛地用于两因素之间相关程度的计算[15]。具体计算过程如下：

步骤1 将第i条地震动的某一地震动强度指标值记为Ii；

步骤2 采用有限元法计算边坡模型在第i条地震动输入下的边坡最大地震响应值Ri；

步骤3 重复步骤1和步骤2，得到所有地震动记录的Ri及其对应的Ii；

步骤4 将所有地震动的计算结果画在R-I坐标系中，并通过式(3)计算得到R与I之间的pearson相关系数r。

(3)

式中：r为各地震动参数的影响权重，r越接近1.0，则说明其相关性越好，即用该地震动强度指标来计算边坡地震响应就越合理。

2 模型建立及计算参数

2.1 模型建立

为研究边坡在地震作用下的动力响应特性，建立如图1的二维土坡模型。并沿土坡坡面处布设5个观测点。模型长×高=170 m×70 m，边坡坡角为34°，坡高30 m，边坡坡顶后缘长为80 m。根据Lysmer等[16]的研究成果，岩土体模型网格尺寸受输入地震波的最短波长控制，网格最大尺寸应小于最短波长的1/8～l/10。本构模型为理想弹塑性本构模型，屈服准则采用适用于岩土体的力学行为的摩尔-库仑强度准则。为充分研究边坡在地震作用下的响应规律，模型材料假定为均质材料，边坡土体的力学参数见表1。

对模型进行静力计算获得自重应力场并平衡后，进行边坡地震动力响应计算。在模拟分析边坡等半无限体的动力问题时，为了防止地震波传播到模型边界处反射回模型，通常需要设置人工边界来实现必要的能量发散[17]，因此模型边界设置黏弹性边界，即在边界处设置弹簧和阻尼单元。模型的阻尼采用工程中常用的Rayleigh阻尼形式。

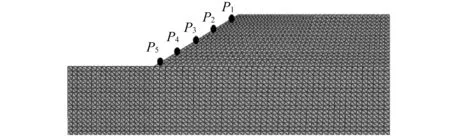
图1 边坡模型示意图Fig.1 Finite element mesh

参数密度/(kg·m-3)弹性模量/MPa泊松比黏聚力/kPa内摩擦角/(°)数值207090．80．313．9925

2.2 地震动选取

本文从太平洋地震研究中心数据库里共随机选取了100条具有不同地震动参数特性的原始地震动记录，并分别对各条地震动记录进行积分、傅里叶变换等计算处理以统计其PGA、PGV、阿里亚斯强度(AI)、累积绝对速度(CAV)、持时和特征周期。经计算可知，所选取的地震动记录中加速度峰值PGA变化范围为0.004 1～1.225 9g，PGV范围为0.378～112.376 cm·s-1，阿里

亚斯强度范围为0.000 4～8.887 9 m·s-1，CAV 范围为0～0.285 7 g·s，持时[18]的范围为0.21～46.12 s，特征周期范围为0.09～2.00 s。由此可见，这100条地震动的参数变化范围较大，具有较大的随机性。本文将上述每条原始地震动记录进行基线矫正后作为输入来计算边坡的响应，进而展开对地震动不同强度指标影响权重的研究分析。

3 结果分析

将以上处理后的100条地震动记录作为输入，模拟计算边坡的地震响应。本文将边坡观测点的最终变形位移和坡顶输出加速度作为边坡响应的代表值来研究地震动各参数对边坡地震响应的影响。

3.1 地震动参数的影响规律

提取边坡5个观测点在各地震动作用下的最终位移和坡顶处P1点的加速度放大系数，研究其随地震动峰值加速度(PGA)、地震动峰值速度(PGV)、阿里亚斯强度(AI)、绝对累积速度(CAV)、持时和特征周期的变化规律。限于篇幅，且结果显示变化规律相似，本文只列出了坡顶处P1点的最终变形位移和加速度放大系数随地震各参数的变化规律，如图2～图7所示。

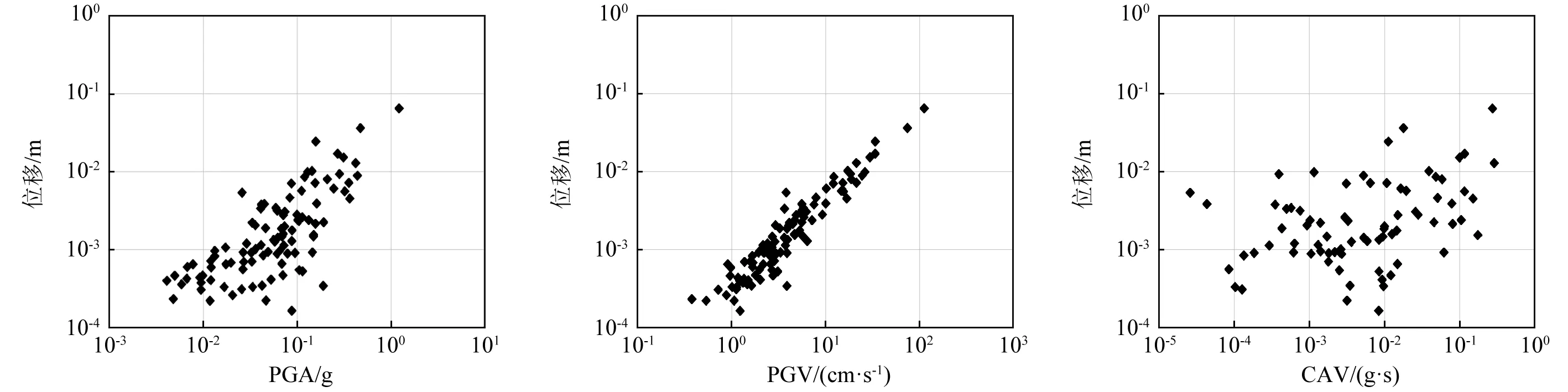
图2 P1点变形位移随PGA的变化 图3 P1点变形位移随PGV的变化 图4 P1点变形位移随CAV的变化Fig.2 Variation of P1 displacement with PGA Fig.3 Variation of P1 displacement with PGV Fig.4 Variation of P1 displacement with CAV

图5 P1点变形位移随阿里亚斯强度的变化 图6 P1点变形位移随地震动持时的变化 图7 P1点变形位移随地震动特征周期的变化 Fig.5 Variation of P1 displacement with Fig.6 Variation of P1 displacement Fig.7 Variation of P1 displacement Arias intensity with duration with characteristic period

由图2～图7可知，坡体变形位移响应对各地震动参数的敏感度存在显著差异，在整体上随着地震动峰值速度(PGV)、地震动峰值加速度(PGA)和阿里亚斯强度(AI)呈现增大而增大的变化规律，表明以这三个指标的强弱均可以来描述地震对斜坡稳定性的影响程度。同时坡体变形位移对三者变化的敏感度有所不同，其中地震动峰值速度(PGV)与坡体变形位移响应存在着明显的相关性，两者分布均匀且近乎成斜直线。而地震动绝对累积速度(CAV)、持时和特征周期值与坡体变形位移的分布较为杂乱，似乎也存在着一定正相关性，但影响规律不明显。

由图8～图13可知，不同地震动作用下坡顶加速度放大系数整体仅随着地震动持时和特征周期的变化呈现出一定的规律，表现出较强正相关性，即随着地震动持时和特征周期的增大，坡顶加速度放大系数总体也是增大的。但当地震动特征周期大于1.7 s时，坡顶加速度放大系数呈现出逐渐减小的趋势。地震动峰值加速度(PGA)、地震动峰值速度(PGV)、阿里亚斯强度(AI)以及绝对累积速度(CAV)对坡顶加速度放大系数的影响则较小，表现出的规律性不强。

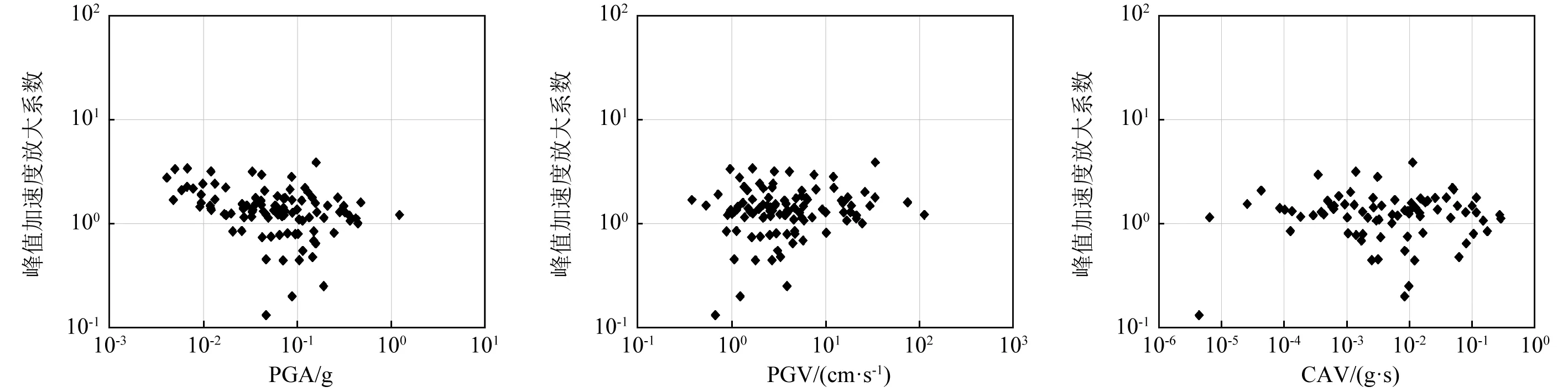
图8 P1点加速度放大系数随PGA的变化 图9 P1点加速度放大系数随PGV的变化 图10 P1点加速度放大系数随CAV的变化 Fig.8 Variation of P1 displacement Fig.9 Variation of P1 PGA amplification Fig.10 Variation of P1 PGA amplification with PGA coefficients with PGV coefficients with CAV

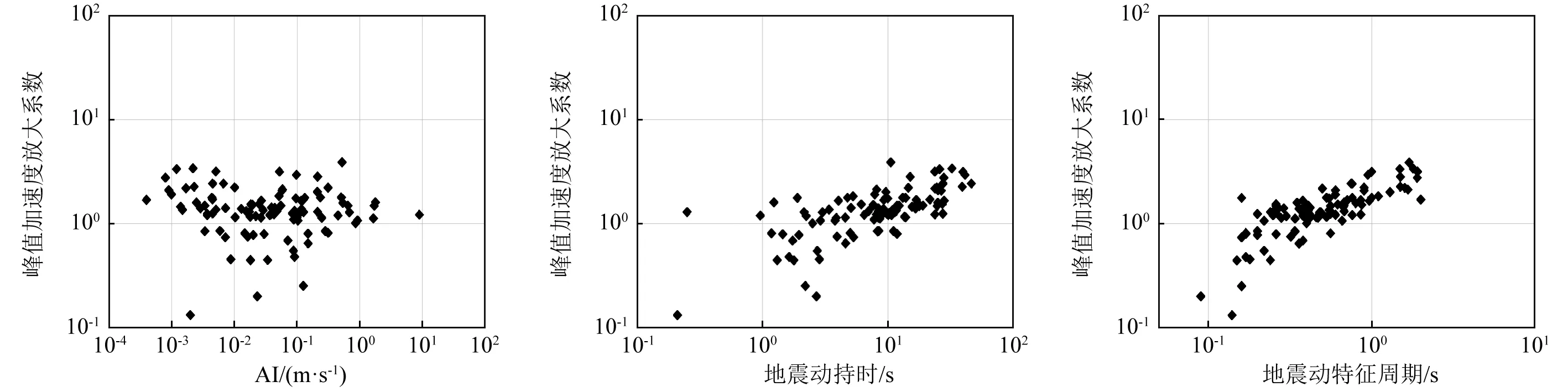
图11 P1点加速度放大系数随阿里亚斯 图12 P1点加速度放大系数随地震 图13 P1点加速度放大系数随地震 强度的变化 动持时的变化 动特征周期的变化 Fig.11 Variation of P1 PGA amplification Fig.12 Variation of P1 PGA amplification Fig.13 Variation of P1 PGA amplification coefficients with Arias intensity coefficients with duration coefficients with characteristic period

3.2 地震动参数影响权重性研究

上述分析表明地震动各参数对边坡地震响应的影响程度是不同的。为进一步研究分析各参数对边坡地震响应的影响敏感度，本文计算了边坡各位移监测点在不同地震动作用下的最终位移和坡顶加速度放大系数与地震动峰值加速度(PGA)、地震动峰值速度(PGV)、阿里亚斯强度(AI)、绝对累积速度(CAV)、持时和特征周期值的相关系数，如表2所示。

通过对上表中相关性计算的结果进行研究分析，可以认为：

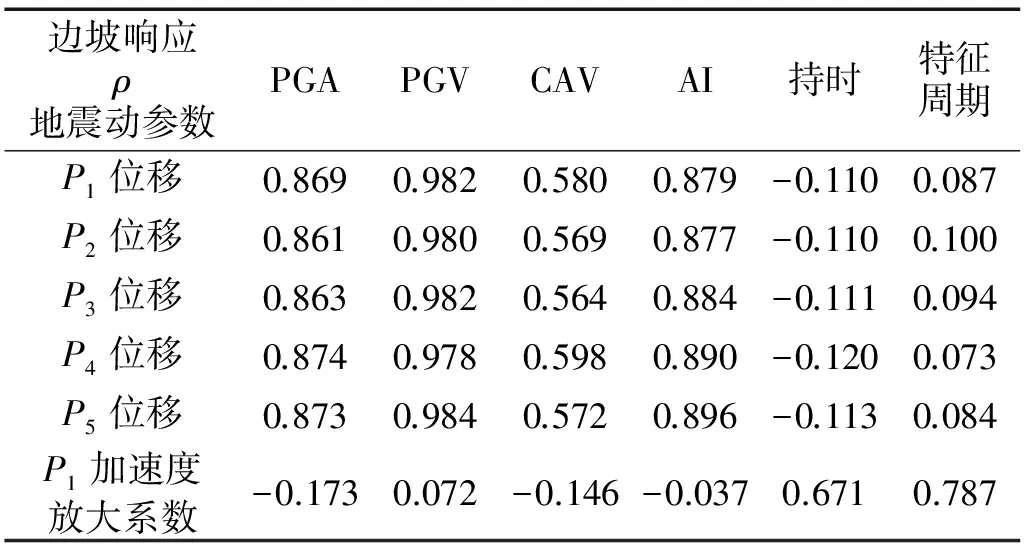
表2 地震动参数和边坡地震响应的相关系数

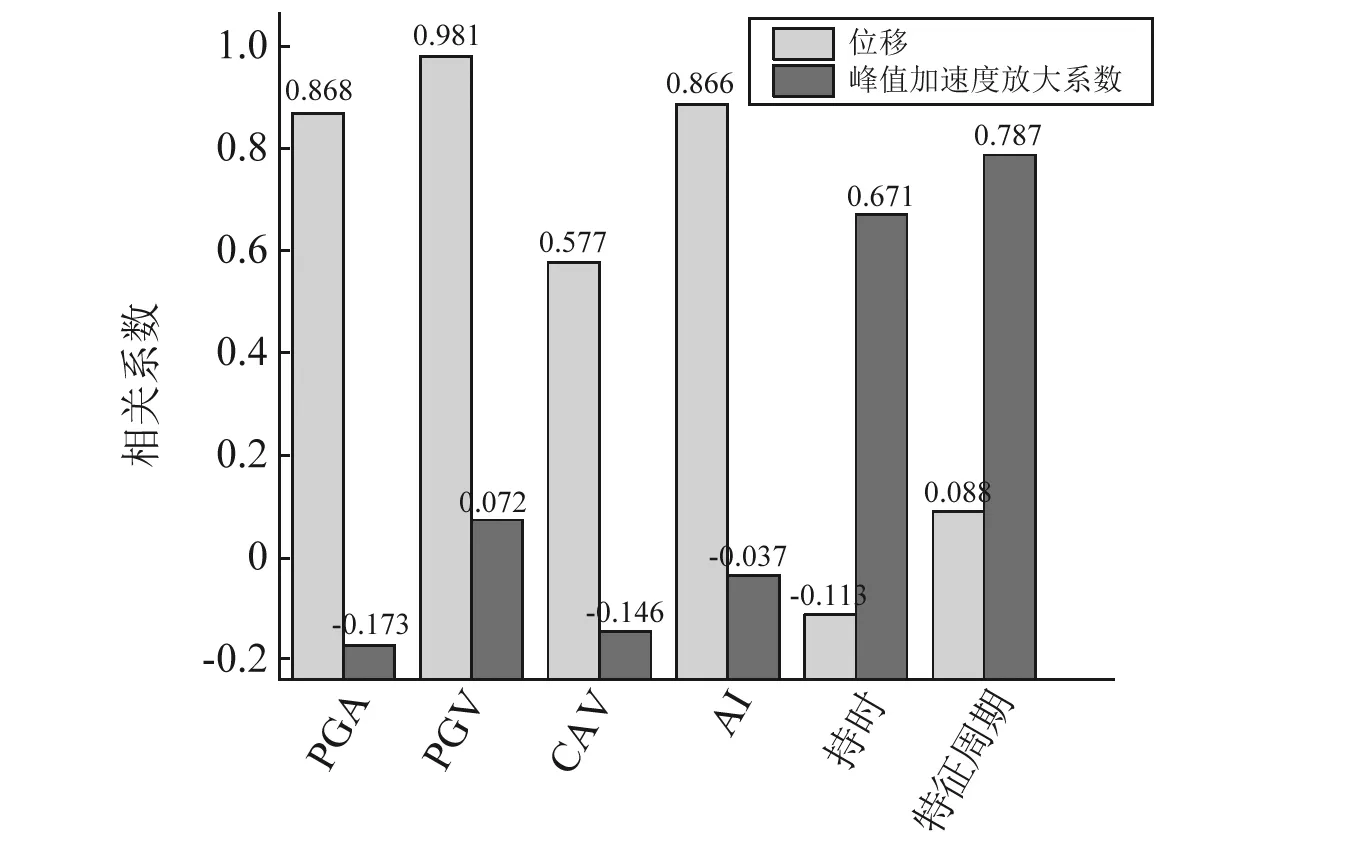
图14 地震动参数与土坡变形位移和加速度放大系数的相关系数Fig.14 The correlation coefficient between slope seismic response and ground motion parameters

地震动峰值速度(PGV)与坡体五个位移监测点的响应的相关性最高，相关系数在0.979～0.985，平均值为0.981，接近于1。地震动速度与质点运动的能量是具有直接关系的，因而PGV可以在一定程度上反映震时地表震动释放能量的强度，也就决定了对土坡作用的大小；其次为阿里亚斯强度(AI)，相关系数在0.877～0.896，平均值为0.886。由于阿里亚斯强度是一个综合了地震动中所有震动幅值和持时的指标，因此它更好地表征震动释放的能量对土坡响应的影响程度；地震动峰值加速度(PGA)对土坡位移响应的相关程度仅次于阿里亚斯强度(AI)，其相关系数在0.861～0.874，平均值为0.868。PGA是目前工程中被运用最为广泛的一个指标，获取较为方便，且很大程度上可以描述地震动的强弱，但由于峰值加速度具有随机的特点，离散性很大，而且会发生临近震中或断层的饱和现象[19]，例如处于高频上的加速度峰值则对土坡的影响则较小，因此将PGA作为强度指标来研究土坡稳定性时应考虑地震动的频谱特性。绝对累积速度(CAV)是潜在破坏作用的地面加速度绝对值在整个地震时间历程上的积累，多用于核电结构的地震分析中，与土坡位移响应的相关系数在0.564～0.598，平均值为0.577，相比之下两者相关程度不是很高。而持时和特征周期与土坡位移响应的相关系数则更低，即它们的大小对土坡位移的影响相对较小。

(2)坡顶加速度放大系数与地震动特征周期和持时有着较高的相关性，相关系数分别为0.787和0.671。其中特征周期的相关系数最高，这可以用共振现象来解释。而地震动峰值加速度(PGA)、地震动峰值速度(PGV)、阿里亚斯强度(AI)和绝对累积速度(CAV)四个指标对其相关程度则较低。

4 结 论

计算分析了土坡在多组地震动作用下的动力响应，得到了地震动峰值加速度(PGA)、地震动峰值速度(PGV)、阿里亚斯强度(AI)、绝对累积速度(CAV)、持时和特征周期对土坡位移和加速度放大系数的相关系数，通过探讨其相关性和影响规律，得到以下结论：

(1)对于土坡坡面的变形位移响应，与其相关性较高的三个参数依次为地震动峰值速度(PGV)、阿里亚斯强度(AI)和地震动峰值加速度(PGA)，其平均相关系数分别为0.981、0.886、0.868，且均呈现正相关现象。绝对累积速度(CAV)、持时和特征周期也对土坡坡面位移响应有一定的影响，但是敏感度相对较低。因此在选用地震参数指标研究土坡地震响应或灾害评估时应优先考虑地震动峰值速度(PGV)、阿里亚斯强度(AI)和地震动峰值加速度(PGA)这个强度指标。

(2)对于土坡坡顶加速度响应，与其相关性较高的两个参数依次为地震动的特征周期和持时，相关系数分别为0.787和0.671，呈现正相关现象。但当特征周期超过1.7 s时，此时地震对土坡作用减小，因此坡顶加速度放大系数出现逐渐下降的趋势。其他地震动参数对土坡坡顶加速度响应的影响相对较小。

[ 1 ] 李忠生.国内外地震滑坡灾害研究综述[J].灾害学,2003,18(4):64-70.

LI Zhongsheng. The state of the art of the research on seismic landslide hazard at home and abroad[J]. Journal of Catastrophology, 2003, 18 (4):64-70.

[ 2 ] HARP E L, WILSON R C. Shaking intensity thresholds for rock falls and slides: evidence from 1987 Whittier Narrows and Superstition Hills earthquake strong-motion records[J]. Bulletin of the Seismological Society of America ,1995,85(6): 1739-1757.

[ 3 ] WILSON R C, KEEFER D K. Predicting areal limits of earthquake-induced landsliding[M]∥Evaluating Earthquakes Hazards in the Los Angeles Region—an Earth-Science Perspective. Washington: USGS Professional,1985:317-345.

[ 4 ] 祁生文,伍法权,孙进忠,等.边坡动力响应规律研究[J].中国科学E辑,2003,33(增刊1):28-40.

QI Shengwen, WU Faquan, SUN Jinzhong. Study on the dynamic response characteristic of slope[J].Science in China, Ser. E, 2003, 33 (Sup 1): 28-40.

[ 5 ] 殷跃平.汶川八级地震滑坡特征分析[J].工程地质学报, 2009, 17(1): 29-38.

YIN Yueping. Features of landslides triggered by the 8.0 Wenchuan earthquake[J]. Journal of Engineering Geology， 2009， 17(1): 29-38.

[ 6 ] 王秀英,聂高众,王登伟，等.汶川地震诱发滑坡与地震动峰值加速度对应关系研究[J].岩石力学与工程学报,2010,29(1):82-89.

WANG Xiuying, NIE Gaozhong, WANG Dengwei. Research on relationship between landslides and peak ground accelerationsinduced by Wenchuan earthquake[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(1):82-89.

[ 7 ] 言志信，张森，张学东，等.顺层岩质边坡地震动力响应及地震动参数影响研究[J]. 岩石力学与工程学报,2011, 30(增刊2): 3522-3528.

YAN Zhixin, ZHANG Sen, ZHANG Xuedong, et al. Study of dynamic response of bedding rock slope under earthquake and influence of ground motion parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Sup2): 3522-3528.

[ 8 ] 李海波,肖克强,刘亚群,等.地震荷载作用下顺层岩质边坡安全系数分析[J].岩石力学与工程学报,2007,26(12):2385-2394.

LI Haibo, XIAO Keqiang, LIU Yaqun,et al. Factor of safety analysis of bedding rock slope under seismic load[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2385-2394.

[ 9 ] 杨峥,许强,刘汉香,等.地震作用下含反倾软弱夹层斜坡的动力变形破坏特征研究[J].振动与冲击,2014,33(19):134-139.

YANG Zheng, XU Qiang, LIU Hanxiang, et al. Dynamic deformation and failure of slopes with an anti-dip weak interlayer under earthquakes[J]. Journal of Vibration and Shock,2014,33(19): 134-139.

[10] 梁双庆,苏立君,王洋.不同坡面角度碎石土斜坡动力响应特征研究[J].振动与冲击,2016,35(21):153-158.

LIANG Shuangqing, SU Lijun, WANG Yang. Dynamic response characteristics of gravel soil slope with different angles of inclination[J]. Journal of Vibration and Shock, 2016, 35(21): 153-158.

[11] 王秀英,王登伟.四川汶川地震诱发滑坡与峰值速度的关系[J].地质通报, 2011, 30(1) : 159-165.

WANG Xiuying, WANG Dengwei． Relationships between the Wenchuan earthquake-induced landslide and peak ground velocity, Sichuan, China[J]. Geological Bulletin of China,2011,30(1): 159-165.

[12] SAYGILI G, RATHJE E M. Probabilistically based seismic landslide hazard maps: an application in Southern California[J]. Engineering Geology,2009,109(3/4):183-194.

[13] 徐光兴, 姚令侃, 李朝红, 等.边坡地震动力响应规律及地震动参数影响研究[J].岩土工程学报,2008,30(6): 918-923.

XU Guangxing, YAO Lingkan, LI Zhaohong, et al. Dynamic response of slopes under earthquakes and influence of ground motion parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 30(6):918-923.

[14] 闫坤伐,卢建华,刘晓燕,等.地震作用下高边坡破坏的振动台试验[J].铁道科学与工程学报,2016,13(12):2396-2404.

YAN Kunfa, LU Jianhua, LIU Xiaoyan, et al. Shaking table test for high slope destruction under earthquake action[J].Journal of Railway Science and Engineering,2016,13(12):2396-2404.

[15] 李雪红,李晔暄,吴迪,等.地震动强度指标与结构地震响应的相关性研究[J].振动与冲击,2014,33(23):184-189.

LI Xuehong, LI Yexuan, WU Di, et al. Correlation between ground motion intensity and structural seismic response[J]. Journal of Vibration and Shock,2014,33(23):184-189.

[16] LYSMER J, KUHLEMEYER R L. Finite dynamic model for infinite media[J].Journal of Engineering Mechanics, ASCE, 1969, 95(4): 859-877.

[17] 李小军,廖振鹏,杜修力.有阻尼体系动力问题的一种显式差分解法[J].地震工程与工程振动,1992,9(4):74-80.

LI Xiaojun, LIAO Zhenpeng, DU Xiuli. An explicit finite difference method for viscoelastic dynamic problem[J]. Journal of Earthquake Engineering and Engineering Vibration, 1992, 9(4): 74-80.

[18] 胡聿贤.地震工程学[M].2版.北京:地震出版社，2006:104-109.

[19] 李小军,彭青,刘文忠.设计地震动参数确定中的场地影响考虑[J].世界地震工程, 2001, 17(4):34-41.

LI Xiaojun, PENG Qing, LIU Wenzhong. Consideration of site effects for determination of design earthquake ground motion parameters[J]. World Earthquake Engineering,2001,17(4):34-41.