变力冲量的教学研究
2011-01-24王礼祥蔡书李东阳
王礼祥 蔡书 李东阳
(西南民族大学预科教育学院 四川 成都 610041)
1 引言
在“普通物理”教学中,我们发现学生在理解冲量概念时总是停留在高中物理水平上,认为冲量的方向总是跟外力的方向一致或冲量的方向由外力的方向确定.再加上一些“普通物理”教材也存在部分误导,如对冲量定义式
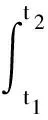
解释说“由于力是矢量,时间是标量,所以力的冲量也是矢量,其方向与力的方向相同.”[1].以致不能正确理解力的冲量反映的是力在一段时间内的时间积累作用,特别是不能突破变力的冲量方向性的教学难点.因此,我们做了以下关于变力冲量的教学研究,供参考.
2 冲量的定义
冲量是描述力对时间的积累作用的物理量,是矢量,而且是一个过程量[2].
2.1 恒力的冲量定义
当物体所受外力为恒力F(单个恒力或多个恒力的合力)时,恒力F在作用时间Δt=t2-t1内的冲量I等于恒力与力的作用时间Δt的乘积,即
I=FΔt=F(t2-t1)
(1)
式(1)表明当F恒定(大小和方向都不变)时,它的冲量I的方向与恒力F的方向一致,即恒力的冲量方向就是恒力F的方向.冲量的这个定义说明:
(1)冲量是过程量,它由外力和力的作用时间共同决定,力的冲量总是对时间或过程来讨论的.
(2)冲量跟参考系选择和受力物体的运动状态无关,因为外力和作用时间都与参考系和物体的运动状态无关.
(3)冲量是矢量[3],既有大小又有方向,叠加合成满足平行四边形法则.外力为恒力条件下,冲量的大小等于恒力的大小与恒力的作用时间乘积,方向与外力的方向一致;对于可简化为质点的物体而言,合力的冲量等于分力的冲量矢量和.即
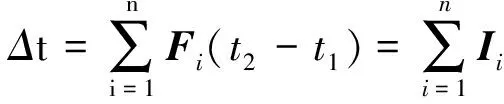
(2)
(4)冲量的作用效果是改变物体的动量.
2.2 微元冲量的概念
微元冲量是指不管物体所受的是恒力还是变力,取一段极短的时间dt作为研究过程;用数学极限表示为

则dt极短到趋于零的时间内恒力与变力都可视为瞬时不变量,于是恒力的冲量定义适用,即
dI=Fdt=F(t)dt
(3)
式(3)表明微元冲量的方向始终与外力的瞬时方向一致.
2.3 变力冲量定义式及分量式意义诠释
一段有限时间间隔内的变力的冲量,原则上可由微元冲量的矢量叠加合成得到.也就是在变力F(t)对物体的作用时间Δt=t2-t1内,将Δt时间间隔平均分成n等分,并计算n个微元冲量矢量的叠加合成,再取n→∞的求和极限计算,即
(4)
式(4)的矢量叠加合成如图1(以二维平面变力为例)所示.
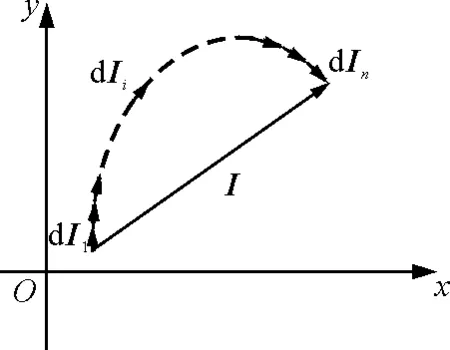
图1
式(4)的分量式可写成如下几种分量形式.
(1)三维直角坐标系分量式
I=Ixi+Iyj+Izk=
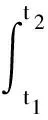
(5)
直角坐标系分量式(5)的特殊之处表现为沿x轴、y轴和z轴正向的单位矢量i,j,k都是恒定不随时间变化的矢量,所以三维变力矢量的冲量直角坐标系分量式计算可类似于方向不变而大小随时间不断变化的力的冲量计算一样处理,即
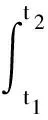
(6)
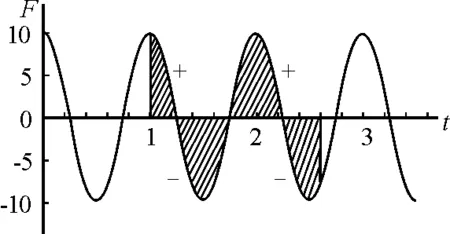
图2
对式(6)采用SI制然后作无量纲化处理:设冲量为I、时间为t、频率为ν、力为F,则I,t,ν,F都不带量纲仅为数学意义的纯数.直观冲量图示为函数F(t)图线与t轴在(t2-t1)段上所围的几何面积,就是数学意义的定积分.图2为受迫振动驱动力(策动力)
F(t)=F0cos2πνt
在无量纲化处理下,取F0=10,ν=1绘制出的t1=1到t2=2.6间隔内变力冲量大小的直观几何面积,如图2阴影所示.此面积可正可负,其正说明冲量方向与规定正方向相同,负为相反.变力冲量的三维分量Ix,Iy,Iz也可正可负,它们表明冲量分量与x轴、y轴和z轴正向相同或相反.
(2)平面曲线运动自然坐标系中的分量式
平面自然坐标系的特点是切向单位矢量τ和法向单位矢量n是随时间变化的.所以平面自然坐标系中变力冲量的分量式为
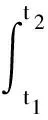
(7)
注意n(t)和τ(t)不能提到积分号外.
平面极坐标系中的变力冲量分量式类似于平面自然坐标系的情形,也是径向单位矢量er和极向单位矢量eθ随时间变化,故在变力冲量的积分表达式中不能把单位矢量提到积分号外,即
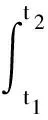
(8)
除非把自然坐标系中的单位矢量分解为用直角坐标系单位矢量来表示,方能回到直角坐标系中简单积分计算变力冲量的分量式.
(3)三维圆柱坐标系中的分量式
三维圆柱坐标系由平面极坐标和与之垂直的z轴构成,所以在三维圆柱坐标系中变力冲量的分量表达式是
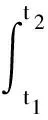
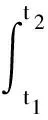
(9)
式(9)中只有Iz分量可以直接积分计算.
(4)三维球坐标系中的分量式
三维球坐标系中单位矢量也是随时不断变化的,所以其分量表达式也只是形式上,除非单位矢量的时间函数是三维直角坐标系单位矢量的显式.球坐标系中的变力冲量分量式是
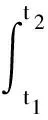
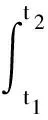
(10)
3 几个变力冲量的算例
3.1 一维变力冲量
【例1】已知质量为m=10 kg的物体位于坐标原点时的初速度为v0=1 m/s,之后物体受到随x坐标变化的力F(x)=10(x+1)(SI)作用而由原点运动到x=10 m处.求此过程中该变力的冲量.
解析:采取无量纲化处理.由冲量定义,此运动过程中变力的冲量为
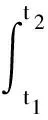
式中t1是物体位于原点x=0处的时刻,t2是物体运动到x=10处的时刻.但x与时间t的函数关系是隐含形式的,不能直接解算,还必须找出x与t的函数关系式.x与t的函数关系可由牛顿第二定律与加速度、速度和位移的关系导出.
根据牛顿第二定律有
(11)
(12)

(13)
对(13)式两边积分,并代入初始条件,有
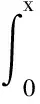
得到
即
v2=x2+2x+1
又因x>0,故可得
v=x+1

上式进行分离变量变为
(14)
ln(x+1)=t
即
x=et-1
可见,当x=0时,t1=0;而x=10时,t2=ln11.所以
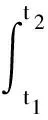
|10et|ln110 =100
故得到变力的冲量
I=100 N·s
3.2 二维变力冲量
【例2】已知做匀速圆周运动的物体所受向心力[4]为F(t)=-10sin(πt)i-10cos(πt)j(SI),求
0~1 s和0~2 s的冲量.
解法1:无量纲化处理.采用直有坐标系冲量定义式
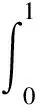


矢量合成如图3和图4.

图3 图4
解法2:采用自然坐标系冲量为
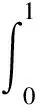
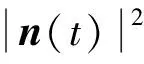
可见,其他坐标系中的冲量分量表达式最终都可回到直角坐标系中进行计算,因为只有直角坐标上的单位矢量是恒矢量,积分时单位矢量可以先提到积分号外去.
4 动量定理
冲量由外力和力的作用时间共同确定,与物体的运动状态和参考系的选择无关.冲量是过程量,它与具体的运动过程或运动时间相联系;讲冲量必须指明是什么过程或具体指定的时间内的冲量.那么,冲量的物理意义是什么呢?下面谈这个问题.
4.1 动量定理的微分形式
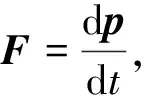
dI=Fdt=dp
(15)
由式(15)知道微元冲量或者冲量元是迫使物体动量改变的原因.冲量为零时动量不变,由过程量(冲量)作用导致物体的运动状态量(动量)的改变,它揭示了外力的瞬时方向与微元冲量的方向或动量的改变方向始终相同.
4.2 动量定理的积分形式
动量定理的微分形式说明在微元过程中外力的微元冲量与物体动量改变之间的关系,同时指明了微元冲量的方向总是与力的瞬时方向一致.对于一个有限的运动过程或一段有限运动时间来说,外力的总冲量(合力的冲量或分力的冲量矢量和)与物体在此过程始末状态时的动量增量之间的关系,即是积分形式的动量定理

(16)
式(16)表明,不论外力是恒力还是变力或变力与恒力的矢量和,它们的总冲量总是等于由于冲量作用而使物体动量改变的增量.
4.3 物体系或质点组的动量定理
动量定理的微分形式或积分形式都只针对以单个物体为研究对象.当把研究对象扩展到物体系或质点组时,系统整体的外力冲量与系统总动量的改变量关系称为物体系的动量定理.它是由单个物体的动量定理引出的.设物体系共有n个物体并对物体编号为1,2,3,…,n,且假设第1个物体所受全部外力的和为F1,全部内力的和为f1;第2个物体所受全部外力的和为F2,全部内力的和为f2;……第i个物体所受全部外力的和为Fi,全部内力的和为fi;……第n个物体所受全部外力的和为Fn,全部内力的和为fn,则由单个物体的动量定理有
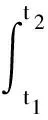
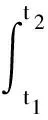
⋮
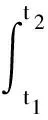
⋮
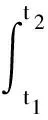
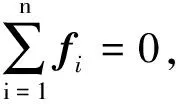
(17)
式(17)即是物体系或质点组的动量定理.它说明系统的总动量改变全是外力冲量作用的结果,系统内力成对出现其冲量互相抵消,内力不改变系统总动量.
应用动量定理可以转换研究对象,改用物体动量改变增量计算力的冲量.比如对例1和例2来说有下面的另解.
例1另解:先由动能定理求末速度,再由动量定理求冲量.由

结合动能定理有
代入数据得
A=600 J
可解出
v=11 m/s
所以依动量定理得
I=mv-mv0=100 N·s
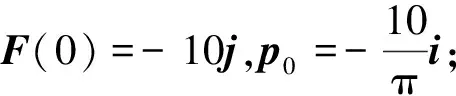
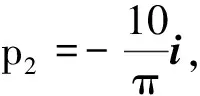
I2=p1-p2=0
1 蔡保平 ,杜乃珍.普通物理学. 北京:化学工业出版社,2007.17~20
2 马冠中, 胡炳元 ,武荷岚. 中美教材中冲量概念比较研究.物理教学,2009(6):64~65
3 门云阁.冲量方向的剖析.河北师范学院学报(自然科学版),1996(1):84~68
4 阚少玲.计算向心力冲量的系列方法.冀东学刊,1995(5):9~12
