地下结构平面问题简化人工边界侧向宽度设置研究

董正方， 朱红云， 闫 超， 郑 彬

(1.河南大学 岩土与轨道交通工程研究所，河南 开封 475004；2.河南大学 循环与功能建材实验室，河南 开封 475004)

一般情况下从震源到人工结构所在位置的距离从几公里到几百公里，由于区域范围过大、地球介质和工程结构的力学性质复杂，进行包括断层和工程结构的动力学分析和计算基本是不可能的。一般是取出一个有限域进行分析和计算，该有限域的边界称为虚拟计算边界。有限元建模时，必须对虚拟边界进行力学上的处理，以使得在虚拟边界上的运动状态与原半无限空间的运动状态一致。这方面的研究工作很多，其中力学上易于理解、有限元计算易于实现、并且表明具有足够工程计算精度的做法是设置黏弹性边界力学元件。

Lysmer等[1-2]开展了较早的研究工作，刘晶波等[3-5]则完成了大量的卓有成效的工作，进而使黏弹性边界的理论得到了系统和全面的论述和实用化。虽然黏弹性边界在计算精度上很高，并且目前使用也最广[6-8]，但黏弹性边界在使用过程中，假定外域介质为均匀线弹性，并且在人工边界处的有限元节点上需要设置一系列由线性弹簧与黏滞阻尼器并联的弹簧-阻尼物理元件，所需要的计算工作量比较大并且比较繁琐。

根据圣维南原理，只要虚拟计算边界距离结构物足够远，则虚拟计算边界处的具体情况对结构地震反应影响就很小，而不必特别精确地处理。因此早期人工边界就是将人工边界的距离取得足够远，在计算时间内不包含边界影响，即远置边界。远置边界至今还常用作其他边界的校核。远置边界操作简单，容易实现，但侧向边界宽度越大，数值计算需要的时间也就越长。远置边界处的约束有三种情况：全部自由，全部约束，竖向约束、水平自由(也称简化边界)，文献[9]中认为上述三种情况都具有足够的可靠性，但需要的侧向边界宽度不同。对侧向边界宽度的取值还没有解析解给出范围，不同研究者对侧向边界宽度的认识存在差异[10-11]。本文将讨论平面地下结构简化人工边界侧向边界宽度的影响因素及其影响程度。

1 理论分析

从无限半平面中取出一有限部分，上部边界取在地表，全部自由；下侧假设刚性基岩，全部约束；侧向边界如果设置成黏弹性边界，则系统的运动方程为

(1)

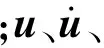
从式(1)可知，黏弹性边界需要在边界离散点上输入应力时程，工作量比较大；且黏弹性边界应用于非线

性问题还有待研究。为了简化，侧向边界可取简化边界，竖向约束、水平自由；基底垂直输入剪切波作用，如图1(a)所示，地震作用下相当于远场侧向边界收到剪应力的作用[12]。从平面模型中任取一个微元体，其应力状态如图1(b)所示。中间任一微元体是纯剪状态，如果取在右侧边界处，则微元体右侧存在一个竖向支座，其支座反力将等于剪应力。如果侧边界取成全部约束或全部自由，则边界处的应力状态将不符合自由场受剪切波作用下的应力状态，因此这种简化边界比全部自由或约束要合理。

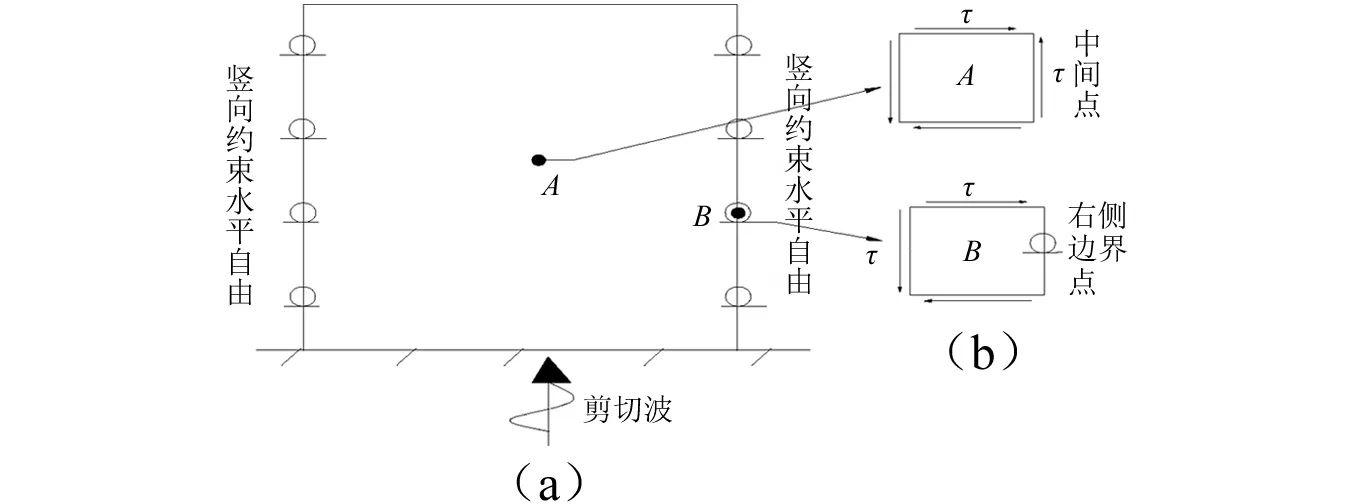
图1 模型示意图Fig.1 Schematic diagram of model

2 影响因素分析

地下结构采用平面模型计算地震反应时，对于侧向边界的宽度大小的影响因素有土体阻尼比、结构尺度、地震波特性、土体非线性等，这些因素中哪些是主要因素、哪些是次要因素、各自的影响程度大小等问题，不能从理论分析中得到解析解答，也不可能通过大量模型试验得到试验解答，只能通过数值模型分析解决，下面应用大型有限元软件ABAQUS进行数值模拟，在分析土体阻尼比、结构尺寸、地震波特性对侧向边界的宽度的影响程度时土体考虑为线性。

2.1 典型案例

为了反映分析结果的一般性，案例选用三种不同的土层，分别为均匀土层、一般厚度(25 m)成层土和深厚土层(64 m)成层土，土层和结构参数见图2。

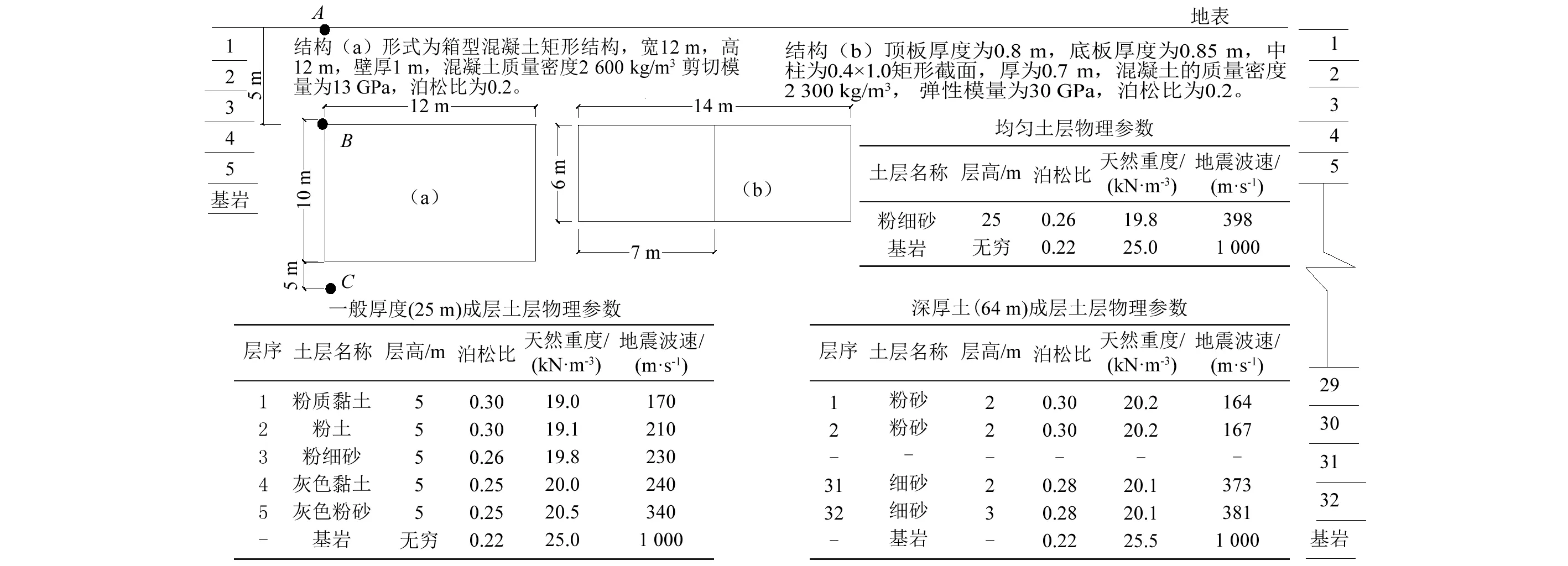
图2 土层及地下结构参数Fig.2 Soillayer and underground structure parameters

土体单元为四结点平面应变单元，结构为梁单元，土体网格根据模型大小变化，均匀土层和一般厚度土层网格大小一致，括号内的为深厚土层，距结构1 000(500) m范围内为1 m×1 m，4 000 m范围内为5 m×1 m，8 000 m范围内为10 m×1 m，在网格尺寸变化处采用不超过1.5倍的网格尺寸进行过度，模型示意图见图1(a)。采用由质量矩阵和刚度矩阵线性组合的瑞利阻尼，假定基岩刚性，地震波从基岩面垂直入射，地震动参数见图3，进行动力时程分析。

图3 地震动参数Fig.3 Ground motion parameters

为了衡量计算精度，取土层中的三个点A、B、C的位移的误差的平均值，位置见图2，b为土层宽度，H为土层厚度，定义最大值误差和均方误差分别为

(2)

(3)

式中：r0(t)为基准模型的反应；r(t)为虚拟计算边界位置不同时的反应。

2.2 土体阻尼比

土体选用均匀土层、一般厚度成层土和深厚土层成层土，土层参数见图2，结构选用结构(a)，改变不同的阻尼比，阻尼比分别为0%、5%和20%，取第二阶和第四阶振型频率确定模型参数，两阶振型的阻尼比取值相同。侧向边界宽度(单侧)分别置于50 m、200 m、500 m、1 000 m、2 000 m、4 000 m和8 000 m处，相对误差以8 000 m模型为基准。基岩处地震波采用Elcentro波，地震动参数见图3，峰值加速度为0.2g。土层反应位移误差见图4，结构反应内力误差见图5。

图4 土层反应位移误差图Fig.4 Soil displacement errors

由图 4位移误差分析可得：①无阻尼时所需宽度较大，阻尼比由5%增大到20%，所需边界宽度变化不明显；②从最大值误差看，对于5%阻尼比，即使是深厚土层成层土，取b/H=6，误差在2.5%以下；③从均方误差看，侧向边界宽度要求大，这主要是波形累积的影响。

由图 5内力误差分析得：①对均匀土层最为明显，无阻尼时所需宽度较大，阻尼比由5%增大到20%，所需边界宽度变化不明显；②对于5%阻尼比，误差在1%以下时，均匀土层需要b/H=4，一般厚度成层土需要b/H=8，深厚土层成层土需要b/H=16。

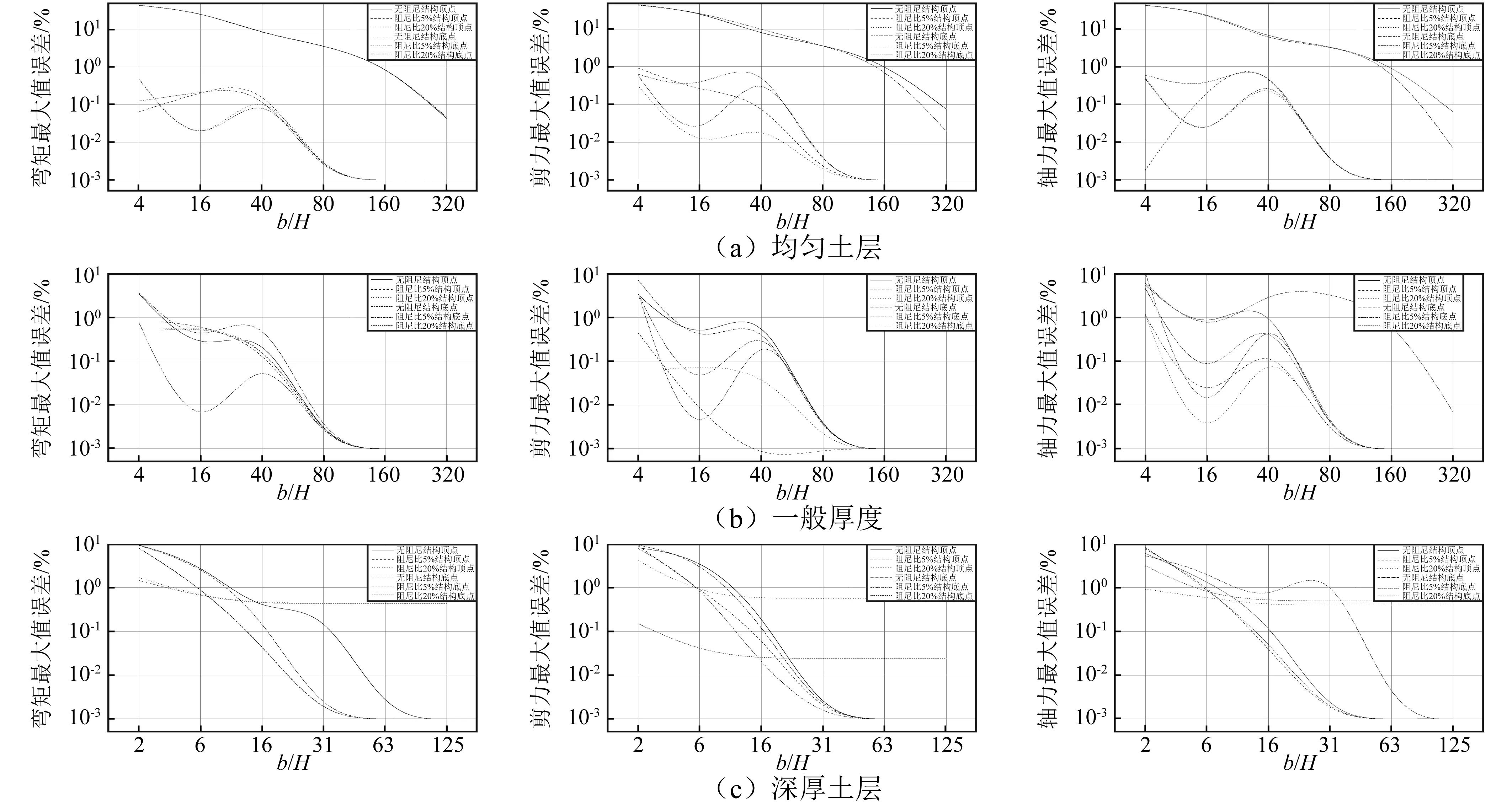
图5 结构反应内力误差图Fig.5 Structural internal force errors

2.3 结构尺度

为了研究结构尺度对侧向边界宽度的影响，取长50 m、宽30 m的结构(a)，结构埋深为地面以下5 m。土体阻尼比取5%，土层选用深厚土层成层土，土层参数见图2。侧向边界宽度(单侧)分别置于50 m、200 m、500 m、1 000 m、2 000 m、4 000 m和8 000 m处。相对误差计算以8 000 m模型为基准。

土层反应位移误差和结构反应内力误差见图6。

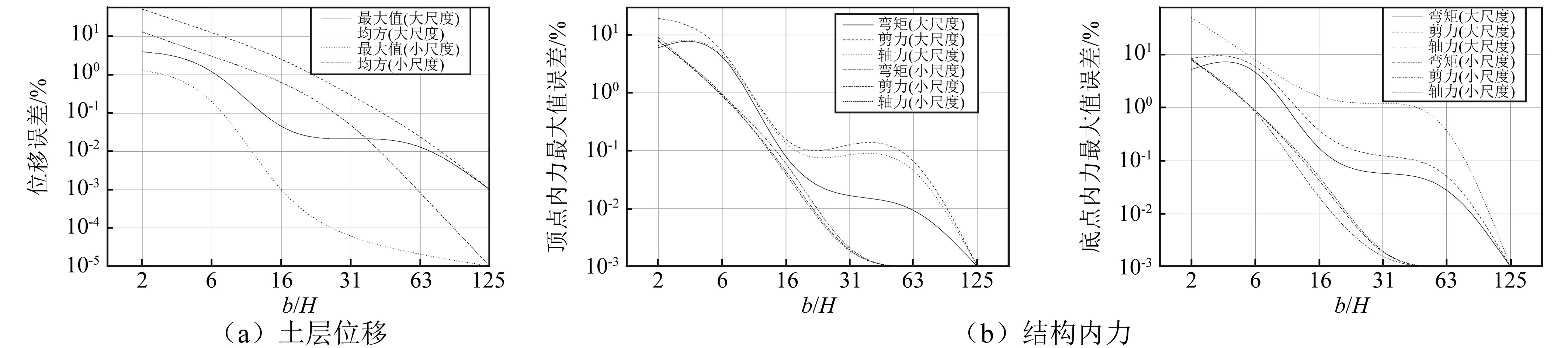
图6 反应误差图Fig.6 Reaction errors

由上图位移误差分析得：①大尺度结构所需边界宽度较大；②从最大值误差看，取b/H=6倍时，大尺度结构误差在1%以上，而小尺度结构误差在1%以下；②从均方误差看，取b/H=16倍时，大尺度结构误差在1%以上，而小尺度结构误差在1%以下。

由上图内力误差分析得：①大尺度结构所需边界宽度较大；②从最大值误差看，取b/H=6倍时，大尺度结构误差在1%以上，而小尺度结构误差在1%以下。

2.4 地震波特性

为了研究地震波特性对侧向边界宽度的影响，取三条不同特性(峰值不同，持时不同，频谱特性不同)的强震记录和一条脉冲波来做对比，侧向边界宽度(单侧)分别置于50 m、200 m、500 m和8 000 m处。相对误差计算以8 000 m模型为基准。地震动参数见图3，结构埋深为地面以下5 m，土体阻尼比取5%，选用深厚土层和结构(a)，参数见图2。

土层反应位移误差见图7，结构反应的内力误差见图8。

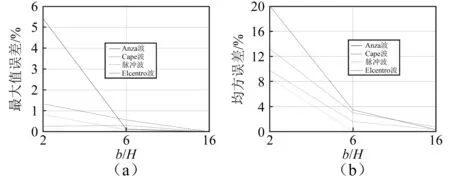
图 7 土层反应位移误差Fig.7 Soil displacement errors

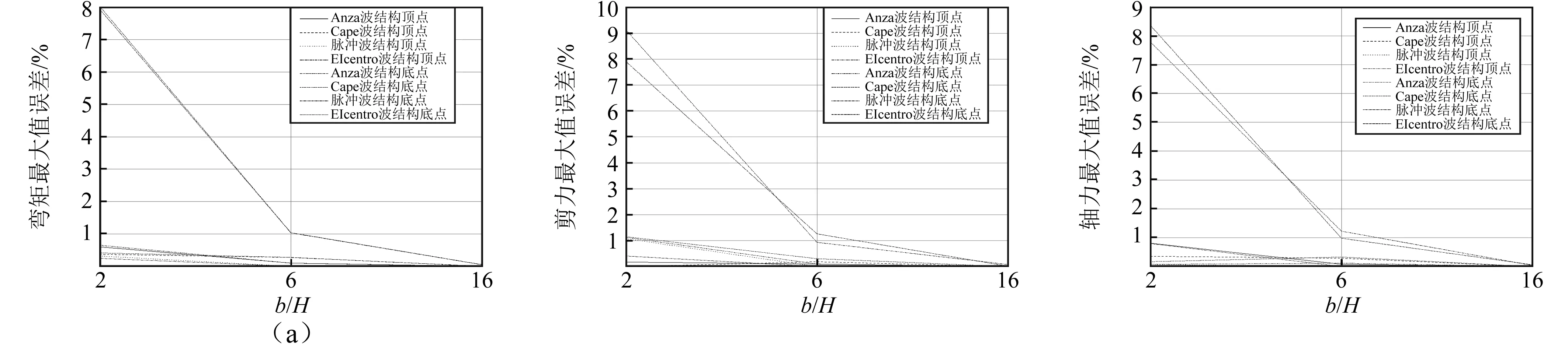
图8 结构反应内力误差Fig.8 Structural internal force errors

由图7位移误差分析得：①当b/H较小时，各个地震波误差离散大，随着b/H的增大，误差离散变小；②从最大值误差看，b/H=6时，四条地震波的位移误差在1%以下；③从均方误差看，b/H=6时，四条地震波的位移误差在5%以下。

由图8结构内力误差分析得：①当b/H较小时，各个地震波误差离散大，持时长的随着b/H的增大，误差离散变小；②从最大值误差看，b/H=6时，四条地震波的内力误差在2.5%以下。

综上，脉冲波和Cape波的频谱特性比较简单，误差较小；Elcentro波持时较长，误差较大。

2.5 土体非线性

土体采用的是Davidenkov骨架曲线的土体动力本构，文献[13]中提出了采用三参数A、B和γ0拟合G/Gmax-γ曲线的试验结果，阻尼取阻尼比值中的最小阻尼比，假定阻尼只与刚度有关，土体动剪切模量比和阻尼比值见表1。

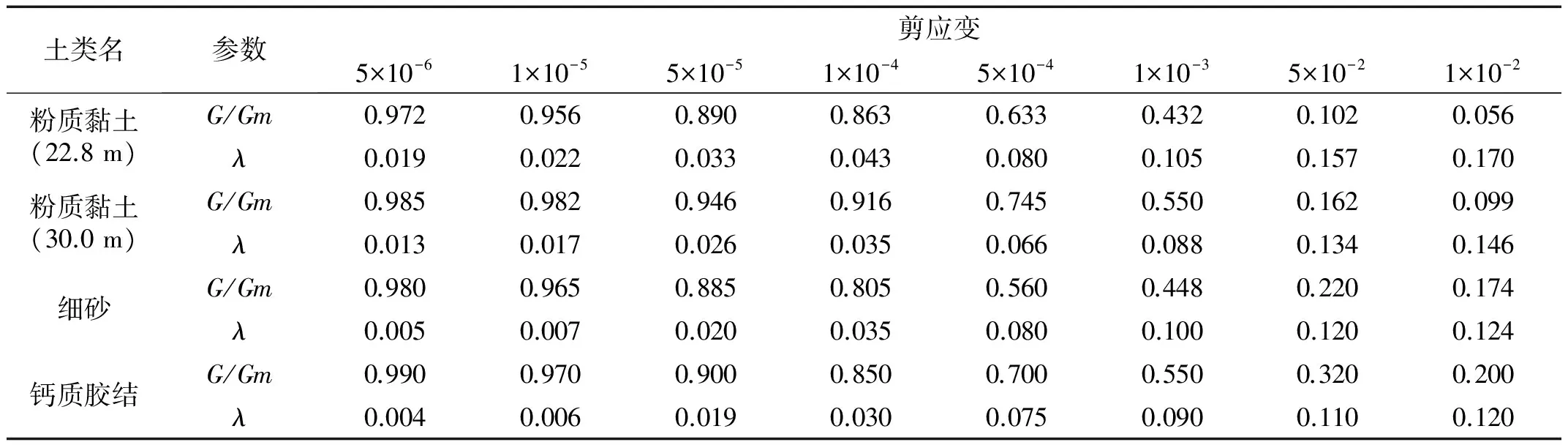
表1 土体动剪切模量比和阻尼比值

为了反映分析结果的一般性，选用25 m厚的均匀细砂土和结构(a)、64 m厚的深厚土层成层土和结构(b)，细砂天然重度20.2 kN/m3，剪切波速298 m/s，泊松比0.30，深厚土层和结构参数见图2。峰值加速度分别为0.03g、0.2g、0.8g，侧向边界宽度(单侧)分别置于25 m、50 m、100 m、200 m、500 m和1 000 m处，相对误差计算以1 000 m模型为基准。地震波采用图3中的Anza波。本构拟合参数见表2。

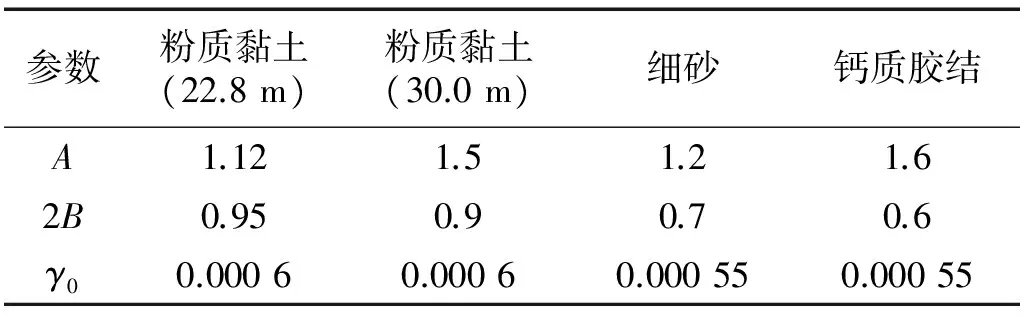
表2 拟合参数

取土层中的三个点A、B、C的位移的误差的平均值，位置见图2，其中深厚土层中C点位置向下移1 m，均匀土层网格为1 m×1 m的均匀网格，深厚土层成层土网格为2 m ×2 m的均匀网格，土层反应位移误差见图9，结构反应的内力误差见图10。

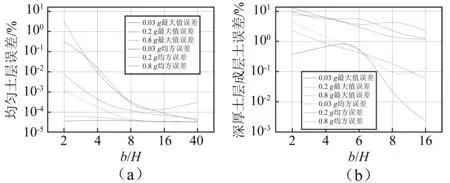
图 9 土层反应位移误差Fig.9 Soil displacement errors

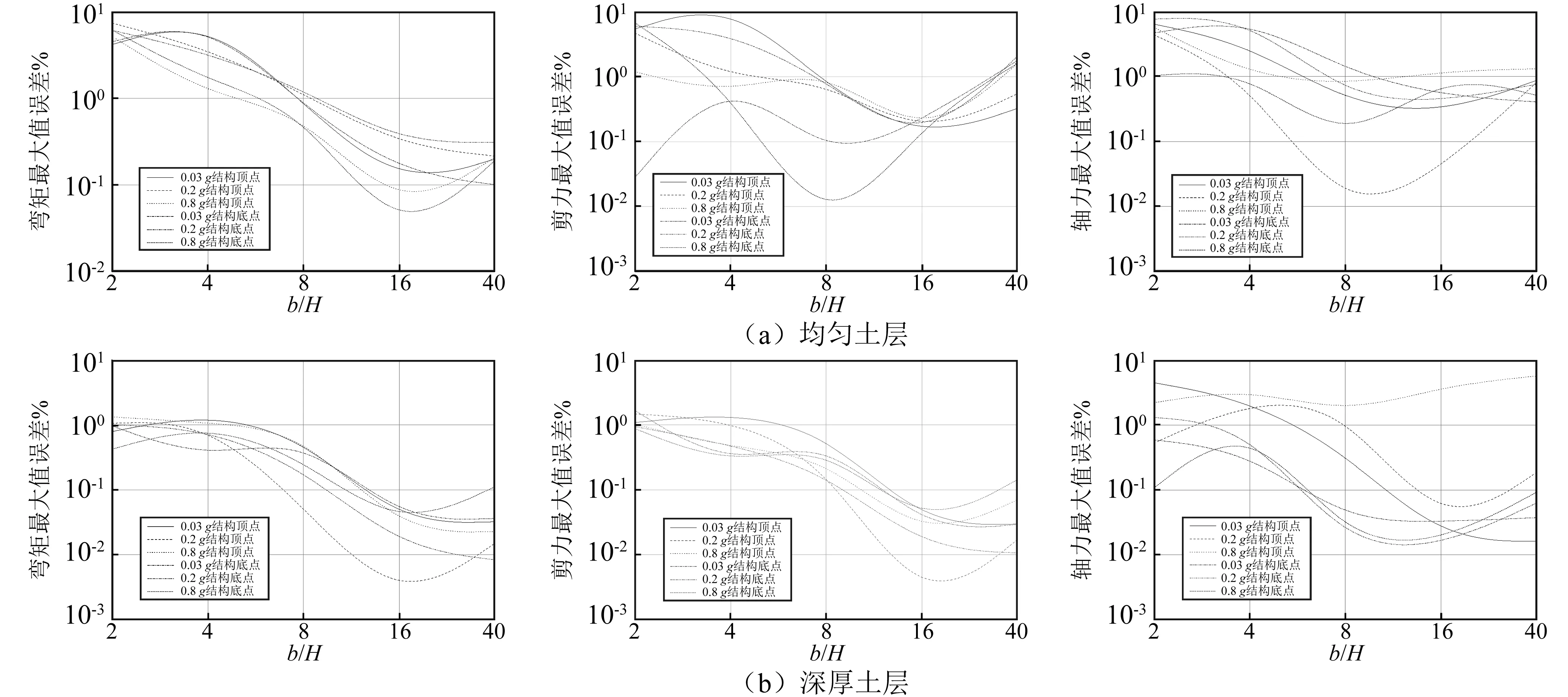
图10 结构反应内力误差Fig.10 Structural internal force errors

由图9位移误差分析得：①在三种峰值加速度情况下，均匀土层当b/H=2时，位移误差基本都在1%以下(除一个点外)；深厚土层成层土当b/H=4时，最大值位移误差在1.5%以下，当b/H=8时，均方误差在5%以下；②当土体进入非线性后，随着非线性程度的增大对边界宽度的影响并不敏感，这和之前讨论阻尼对边界宽度影响时规律一致。

由图10结构内力分析得：①从最大值误差看，b/H=8时，弯矩和剪力的误差都在1.5%，轴力的误差在2.5%；②当土体进入非线性后，随着非线性程度的增大对边界宽度的影响并不敏感。

3 结 论

通过对典型案例进行动力时程分析，得出了地下结构平面问题中侧向人工边界的影响规律：

(1)阻尼比对边界宽度有影响，无阻尼所需边界宽度最大，阻尼到达一定值后，阻尼比的变化对边界宽度的影响不敏感。土体非线性有跟阻尼比类似的影响规律，线性情况下所需边界宽度最大，非线性到达一定程度后，非线性程度的变化对边界宽度的影响不敏感。

(2)结构尺度对边界宽度有影响，结构尺寸越大所需边界宽度越宽。

(3)地震波特性中的频谱特性和持续时间对边界宽度有较大影响；当b/H较小时，各个地震波误差离散大，随着b/H的增大，误差离散变小。

(4)从最大值误差分析，当阻尼比为5%时，考虑所有影响因素时取b/H=40时，误差在1%以下，取b/H=16时，误差在5%以下。

[ 1 ] LYSMER J, KUHLEMEYER R L.Finite dynamic model for infinite media[J]. Journal of Engineering Mechanics, ASCE, 1969, 95(4): 859-877.

[ 2 ] DEEKS A J, RANDOLPH M F. Axisymmetric time-domain transmitting boundaries[J]. Journal of Engineering Mechanics, 1994,120(1): 25-42.

[ 3 ] 刘晶波，吕彦东.结构-地基动力相互作用问题分析的一种直接方法[J]. 土木工程学报，1998,31(3):55-64.

LIU Jingbo, LÜ Yandong. A direct method for analysis of dynami soil-structure interaction[J]. China Civil Engineering Journal, 1998,31(3):55-64.

[ 4 ] 刘晶波，杜义欣，闫秋实. 黏弹性人工边界及地震动输入在通用有限元软件中的实现[C]∥南京工业大学第三届全国防震减灾工程学术研讨会.南京：中国土木工程学会，2007.

[ 5 ] 杜修力，赵密，王进廷. 近场波动模拟的一种应力人工边界[J]. 力学学报，2006,38(1):49-56．

DU Xiuli, ZHAO Mi, WANG Jinting.A Stress artificial wave boundary in FEA for near-field problem[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006,38(1):49-56.

[ 6 ] 麻媛. 重力坝-基岩相互作用系统人工边界动力分析[J]. 人民黄河，2014,36(7):109-111.

MA Yuan. Dynamic artificial boundary analysis of dam-foundation rock interaction system[J]. Yellow River, 2014,36(7):109-111.

[ 7 ] 包锐，周叮，刘伟庆，等. 黏弹性人工边界及其在盆地地震效应研究中的应用[J]. 世界地震工程，2013,29(4):133-140.

BAO Rui, ZHOU Ding, LIU Weiqing, et al. Viscou-spring artificial boundary and its application to study on seismic effect of basin[J]. Word Earthquake Engineering, 2013,29(4):133-140.

[ 8 ] 黄景琦，杜修力，田志敏,等. 斜入射SV波对地铁车站地震响应的影响[J]. 工程力学，2014,31(9):81-88.

HUANG Jingqi, DU Xiuli, TIAN Zhimin, et al. Effect of the oblique incidence of seismic sv waves on the seismic response of subway station structure[J]. Engineering Mechanics, 2014,31(9):81-88.

[ 9 ] 吴艺，房营光.动力边界模型对土与结构非线性动力系统数值计算影响的分析[J]. 科学技术与工程, 2007 ,7(15):3803-3810.

WU Yi, FANG Yingguang. Analysis of dynan is boundary model effects on soil structure nonliiear dynanic systan numerical calculation[J]. Science Technology and Engineeraig, 2007,7(15):3803-3810.

[10] 袁松，王峥峥，周佳媚. 隧道地震动力计算边界取值范围研究[J]. 土木工程学报，2012,45 (11):166-172.

YUAN Song, WANG Zhengzheng, ZHOU Jiamei.Study on the model boundary determination in tunnel′s earthquakedynamic analysis[J]. China Civil Engineering Journal,2012,45 (11):166-172.

[11] 楼梦麟，邵新刚. 应用通用程序计算深覆盖土层地震反应的几个问题[J]. 振动与冲击，2015,34(4): 63-68.

LOU Menglin, SHAO Xingang. Several problems in seismic response calculationof soil layer with deep deposit using general software[J]. Journal of Vibration and Shock, 2015,34(4):63-68.

[12] 片山 幾夫，足立 正信，嶋田 穰，等．地下埋設構造物の実用的な準動的解析手法「応答震度法」の提案[C]∥土木学会年次学術講演会講演概要集.東京:土木學會土木圖書館，1985：737-738．

[13] 陈国兴，庄海洋. 基于Davidenkov骨架曲线的土体动力本构关系及其参数研究[J]. 岩土工程学报，2005,27(8):860-864.

CHEN Guoxing, ZHUANG Haiyang. Developed nonlinear dynamic constitutive relations of soils based on davidenkov skeleton curve[J].Chinese Journal of Geotechnical Engineering,2005,27(8):860-864.