弹体正冲击芳纶纤维层合板模拟研究

贾宝华， 李 革， 徐振洋 ， 郭连军

(1.内蒙古科技大学 土木工程学院，内蒙古 包头 014010；2.辽宁科技大学 矿业工程学院，辽宁 鞍山 114051)

20世纪70年代，复合材料开始在军事防护工程中得到应用[1]。而芳纶纤维因其具有轻质高强(密度小和比强度高)、韧性好、耐冲击性能好、比防护性能(防护性能与其密度之比)高等优点成为复合材料中应用于军事防护工程较为广泛的材料之一，如车辆防护、装甲防护、人体防护等领域均有涉及[2-4]。由芳纶纤维制备的防弹衣又轻又薄，能够大大提高军队的行动能力，同时，芳纶纤维易于染色，可以方便的适应各种场景的隐蔽工作，因此被广泛应用于防弹材料的制备。目前美国、英国等发达国家的防弹衣均大量使用芳纶材质，使得芳纶在国防军工材料中占有重要的地位，成为极具发展潜力的新型防弹材料[5-6]。

陈磊等阐述了复合材料的防弹机理，研究了防弹复合材料的结构，对比了二维和三维复合材料织物结构对防弹性能的不同影响。秦建兵等[7]研究了复合材料层合板的侵彻行为，对比了不同弹头冲击层合板的剩余速度和初始速度的关系以及不同层数层合板对抗弹性能的影响，为制造防弹材料选择合适的厚度提供了很好的理论依据。Lopez-Puente等[8]分别采用实验研究和ABAQUS软件模拟分析了碳纤维层合板正冲击和斜冲击下板的侵彻行为，通过大量有限元计算找到了弹道的极限速度，并提取数值总结出冲击速度与极限速度(子弹穿透层合板后速度刚好为零时的初始速度称为极限速度)的线性关系。Tan等[9]采用实验的方法对比分析了不同弹头侵彻Twaron CT 716二维正交机织复合材料板，发现纤维抗弹性能与弹头形状有关，研究表明弹头越尖层合板最初的破坏面积相对较小。马小敏[10]对比分析了平头弹和球形弹冲击芳纶纤维层合板后的破坏形式，结果表明复合材料失效主要是弹性变形、塑性变形和拉伸断裂及分层失效等多种失效形式。王元博等[11]通过弹道冲击实验研究了Kevlar层合材料的抗弹性能，表明高速冲击下弹头对层合板的冲击几乎没有影响，层合板的不同失效形式主要体现在接近极限速度的低速侵彻。

从已有的研究结果来看，复合材料层合板的抗冲击性能是非常复杂的动力学问题，理论和实验研究比较困难，但有限元软件的出现为此类问题的解决提供了广阔前景。本文采用Abaqus/Explicit软件建立三种不同形状弹体正冲击芳纶纤维层合板的有限元模型，通过对三种子弹剩余速度和初始速度的关系，分析芳纶纤维层合板的抗弹性能，并通过模拟结果分析层合板的破坏形式，揭示其破坏机制，为芳纶纤维层合板的设计和优化提供参考。

1 有限元建模和验证

1.1 有限元建模

(1)子弹模型的建立：为保证冲击时动能相同，统一选取直径为7.62 mm，质量为5.2 g的子弹。通过改变长径比来保证质量的统一，圆柱形弹体、半球形弹体和锥角为90°的平头锥头弹体的长径比分别为1.92、2.26和2.09。子弹的材料参数如表1所示，在Abaqus软件中建立的子弹模型如图1所示。

表1 子弹的材料参数

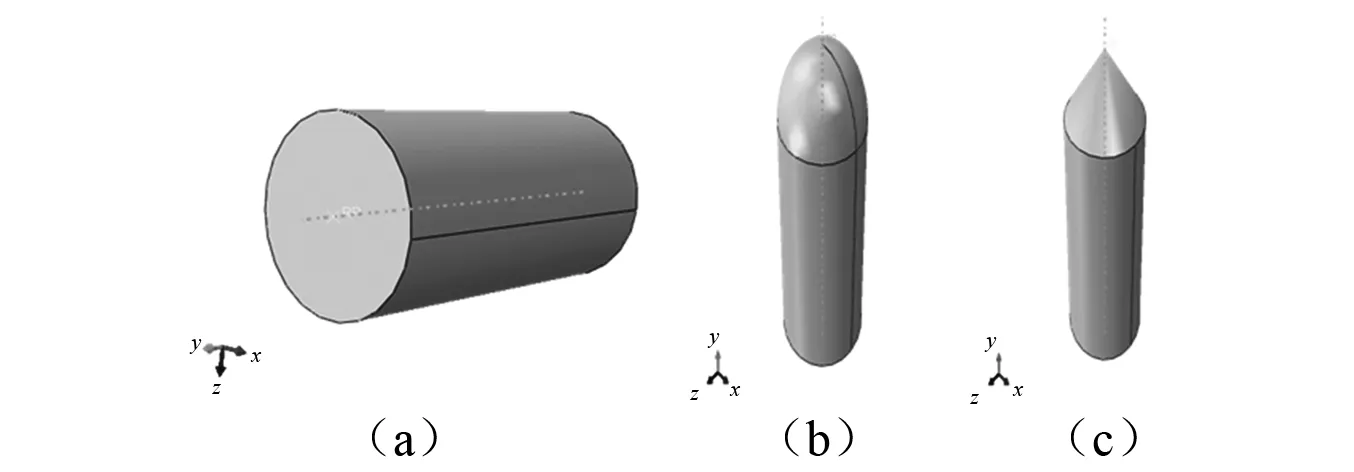
图1 弹体模型Fig.1 The finite element model of projectiles

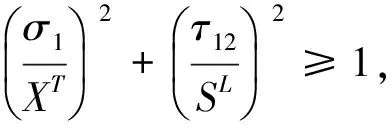
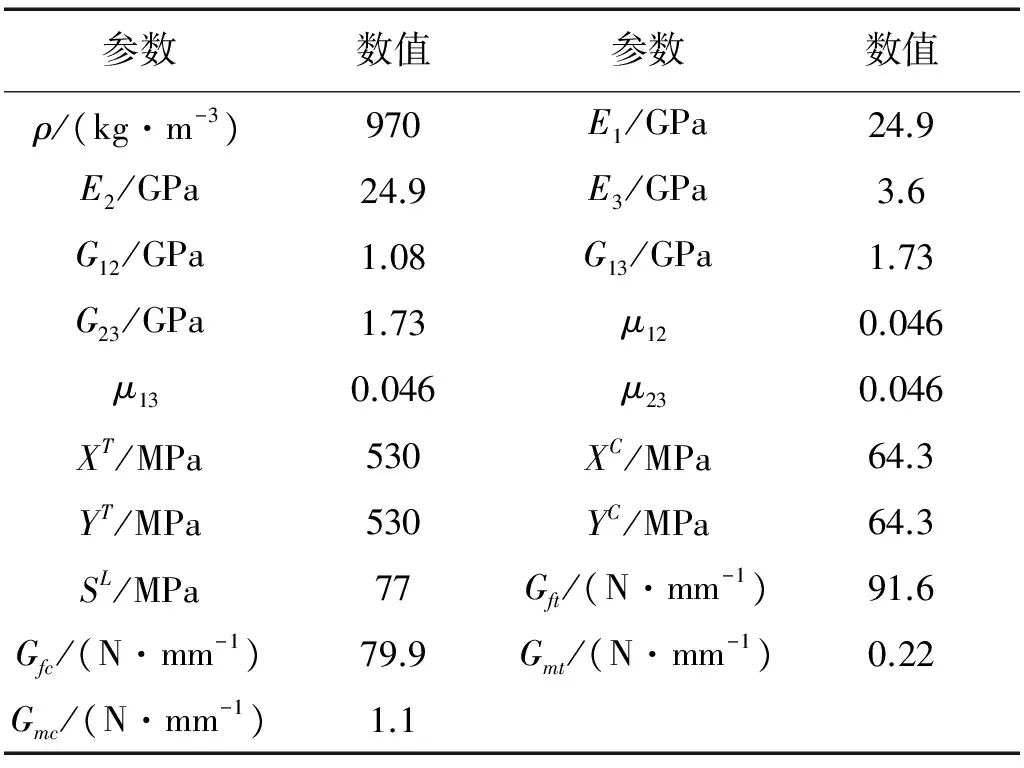
表2 层合板材料参数

本文采用0°和90°交错铺层的方式建立18层的芳纶纤维层合板模型如图2所示。

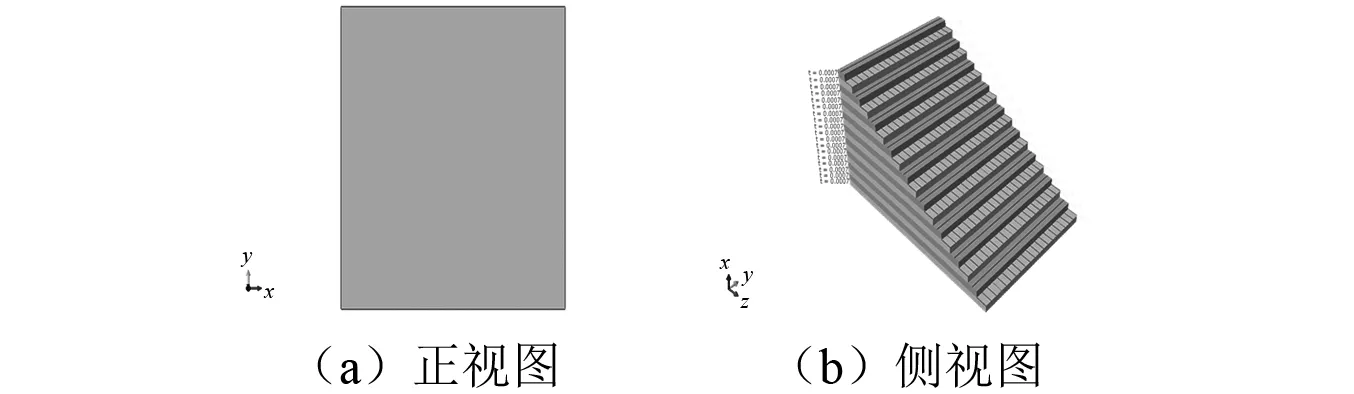
图2 层合板模型Fig.2 The finite element model of laminate

(3)模型装配及载荷施加：将建立的子弹和层合板通过步骤Assembly装配在一起，并通过旋转和平移调整好子弹和层合板的角度和距离。在层合板的四周创建全约束边界条件，在预定义场中将子弹的速度定义只有一个方向(V3方向)速度而其他方向的速度和角速度均为零，通过改变V3方向的速度数值实现不同的速度冲击。模型装配图如图3所示。

图3 模型装配图Fig.3 Model assembly diagram

(4)网格划分：网格的划分直接影响计算速度和计算结果的准确性，为了减少计算时间并保证计算结果的可靠性，划分网格时层合板四周的网格按系统默认值划分，层合板中间承受冲击的部分网格进行细化，采用S4R单元对层合板共划分1 844个单元，层合板网格划分如图4所示。子弹虽然设置成刚体，但在计算时也要划分网格，本文采用C3D8R单元对三种类型子弹分别进行网格划分，最终圆柱形弹体、半球形弹体和锥角为90°的平头锥头弹体被划分成320、680和900个单元。

图4 层合板网格划分图Fig.4 The mesh map of laminate

(5)提交计算：模型建立完成后在步骤Job中创建作业并提交，Abaqus在提交作业后系统会对作业进行检查，经检查无误便可进行有限元分析计算。

1.2 模型验证

为了验证模拟方法的可靠性，本文选用文献[7]中的参数建立平头弹(圆柱形弹体)正冲击复合材料层合板的有限元模型，只是划分单元数与文献中有一定差别，分别模拟了平头弹以初始速度210 m/s、230 m/s、250 m/s和270 m/s四组速度正冲击层合板，提取四组速度的剩余速度与文献中的剩余速度进行对比如表3所示。验证结果表明：在初始速度相同的情况下，本文模拟的剩余速度与文献中的剩余速度误差均在5%以内。而在破坏特征方面，提取了球形弹击穿层合板后的应力云图与文献[7]中的破坏图形进行比较如图5所示，可见他们的破坏特征非常一致。通过对剩余速度和破坏特征的对比，可见本文建立的有限元模型正确，分析方法可靠，故可进行不同弹体正冲击芳纶纤维层合板的有限元分析。

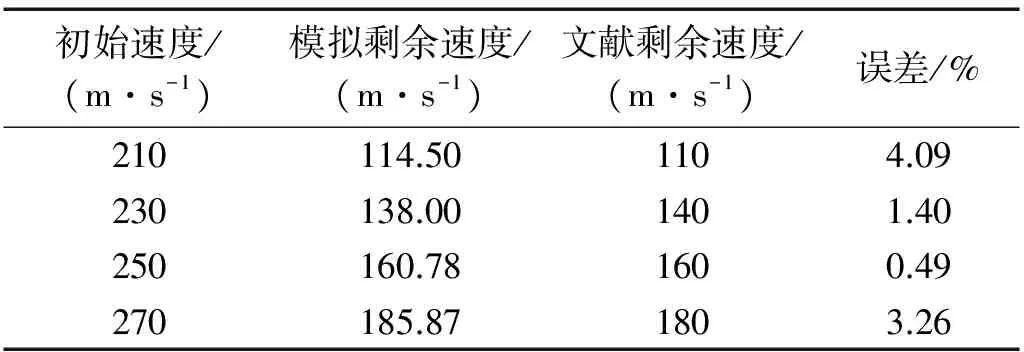
表3 剩余速度数值比较

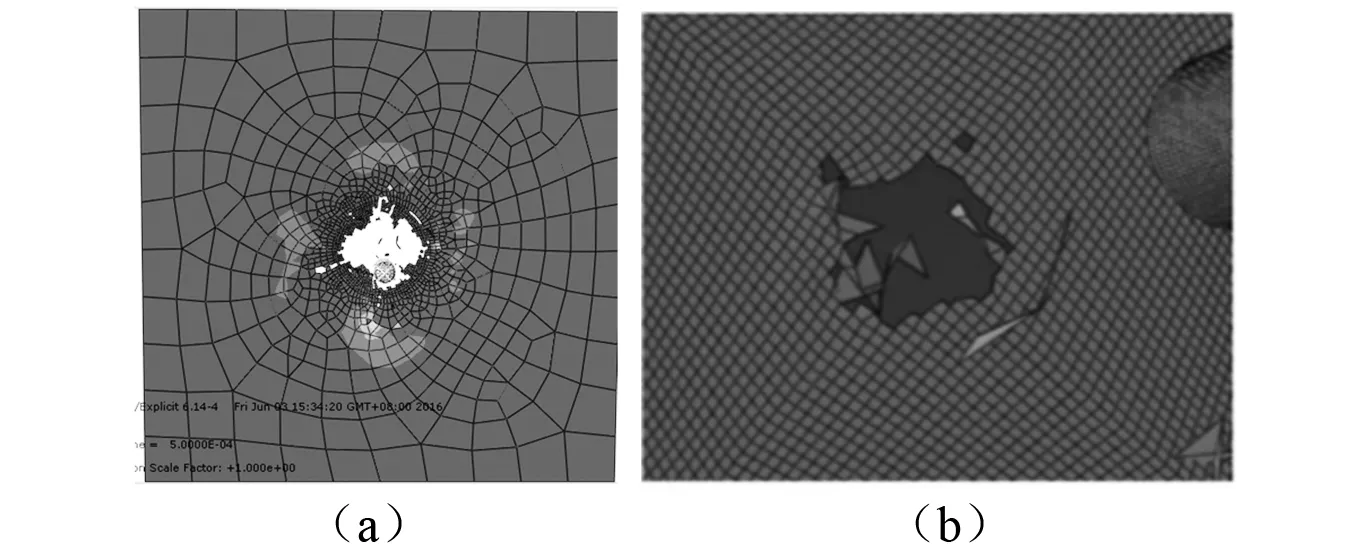
图5 球形弹击穿层合板后的破坏应力云图比较Fig.5 Comparison of failure stress contours of broken laminates by spherical projectile

2 模拟结果分析

2.1 临界速度分析

本文模拟了三种不同形状弹体正冲击芳纶纤维层合板，得到弹体正冲击芳纶纤维层合板初始速度和剩余速度的曲线如图6所示。

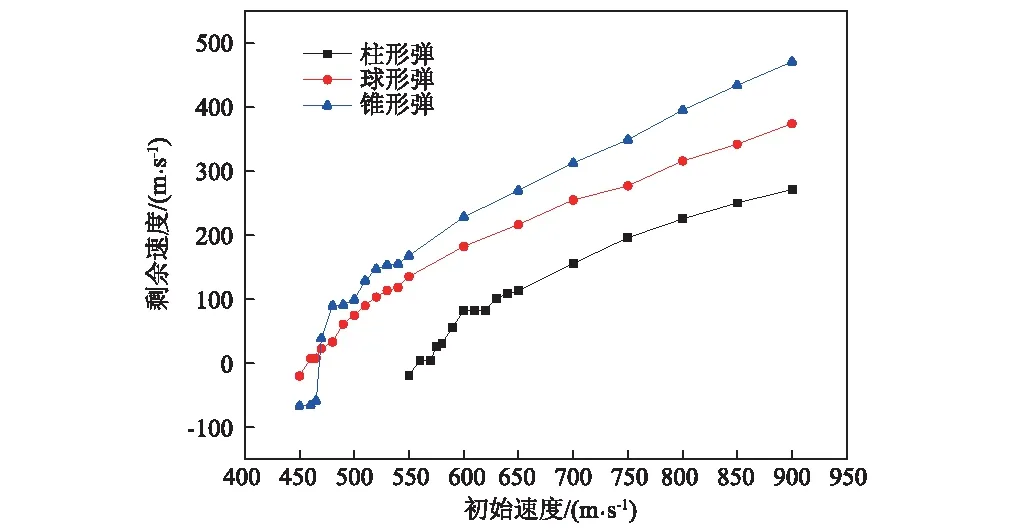
图6 初始速度与剩余速度关系曲线Fig.6 The relation curves for initial velocity with residual velocity

在图6中剩余速度从负值到正值的转变，中间有个剩余速度的零点，其对应的初始速度即为弹体冲击层合板的临界速度，因此由图6可知：柱形弹正冲击层合板的临界速度为580 m/s，而球形弹和锥形弹的临界速度接近，分别为480 m/s和475 m/s，可见柱形弹的击穿能力相对较弱，而球形弹和锥形弹对层合板的击穿能力基本相当。

图7为球形弹以490 m/s的初始速度正冲击层合板时的时间-速度曲线图。从图中可见：子弹的动能损失主要集中在子弹开始冲击芳纶纤维层合板时，速度减小的幅度大，时间短。在子弹完全击穿层合板后速度趋于稳定。柱形弹和锥形弹的时间-速度曲线与球形弹的时间-速度曲线基本相同，可见即使是不同弹体，在正冲击层合板击穿时的动能损失过程却基本相同。

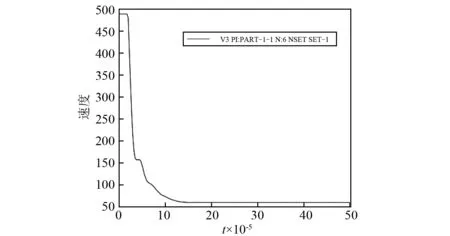
图7 球形弹以490 m/s初速冲击层合板的时间-速度曲线Fig.7 Time vs velocity for spherical projectile impacting on laminate at 490 m/s

2.2 抗弹性能分析

在图6中，当弹体的剩余速度为正数时，表明芳纶纤维层合板被穿透；当弹体的剩余速度为负数时，表明芳纶纤维层合板未被击穿弹体发生了反弹。

由图6通过对比锥形弹和球形弹的初始速度和剩余速度曲线，可以明显观察到两条曲线上下环绕，并且在470 m/s时有交集。 说明锥形弹和球形弹正冲击芳纶纤维层合板的临界速度很接近，但锥形弹穿破层合板后的剩余速度增长趋势较快，而球形弹剩余速度的增长趋势相对较为平缓，可见锥形弹相对球形弹冲击能力较强。

通过图6，可以判断在球形弹、锥形弹和柱形弹中，柱形弹的冲击能力相对较差，但其击穿层合板后的剩余速度趋势与锥形弹和球形弹剩余速度趋势走向基本相似。在三种子弹初始速度相同时，对比三种子弹的剩余速度值，可以发现柱形弹击穿层合板后能量损失相对较多，锥形弹能量损失相对较少，球形弹介于两者之间。表明层合板的抗弹性能与弹体弹头形状有关。

2.3 层合板破坏特征分析

图8为三种不同形状弹体以600 m/s的速度击穿层合板后，层合板破坏的正视图。

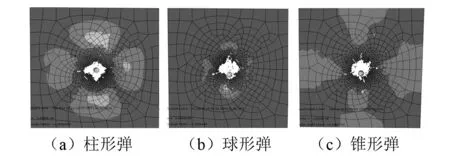
图8 弹体击穿层合板后的破坏应力云图Fig.8 The failure stress contours of broken laminates by different projectiles

由图8可见：柱形弹正冲击芳纶纤维层合板最终的破坏形式为不规则的菱形，球形弹冲击破坏呈现不规则圆形，而锥形弹破坏呈现的是较为规则的圆形。

图9为球形弹以不同速度击穿层合板后，层合板的破坏特征。可以看出：芳纶纤维层合板在子弹较低速度冲击下破坏面积相对较小，破坏形态有规则，在较高速度冲击下，板的破坏面积较大并且破坏形态更趋向不规则，说明在较高冲击速度下，层合板更容易发生断裂失效。

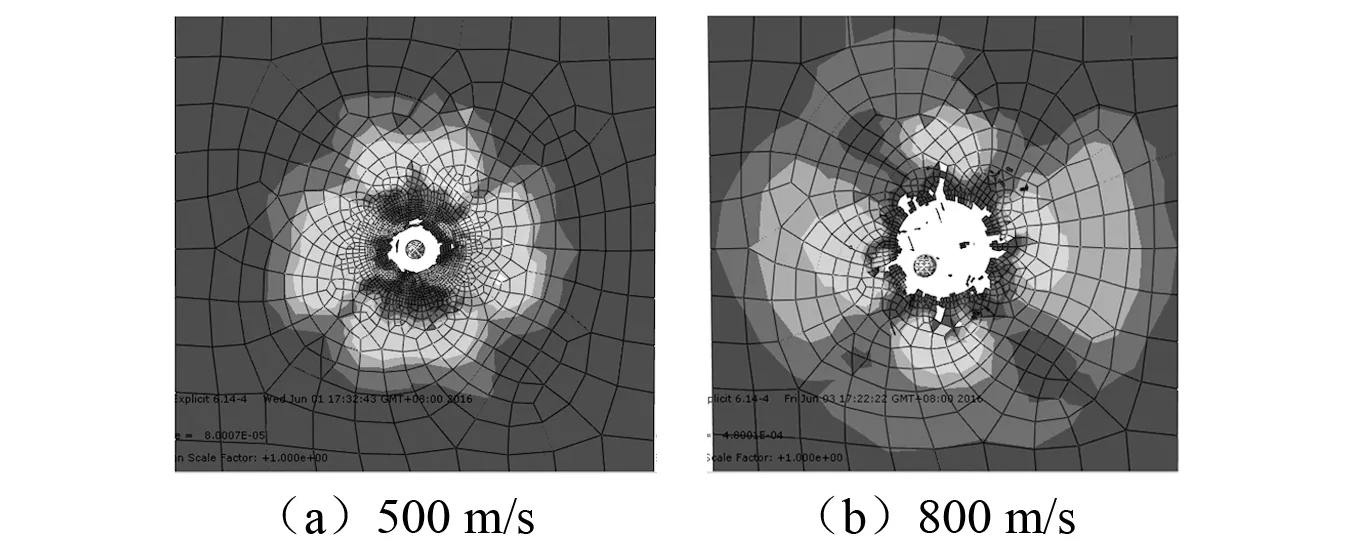
图9 球形弹以不同速度击穿层合板后板的破坏应力云图Fig.9 The failure stress contours of broken laminates by spherical projectile with different velocity

图10为三种形状子弹以600m/s速度击穿层合板时，层合板被击穿瞬间的侧视图。

通过比较层合板破坏侧视图，可看出层合板被柱形弹击穿时其突起变形相对较大，背面的纤维发生拉伸失效，即背面的层合板纤维被拉断。而球形弹和锥形弹击穿芳纶纤维层合板时，层合板的突起相对较小，说明其是先在正面发生基体的压缩破坏，即正面的层合板基体发生压缩失效而产生剪切破坏。

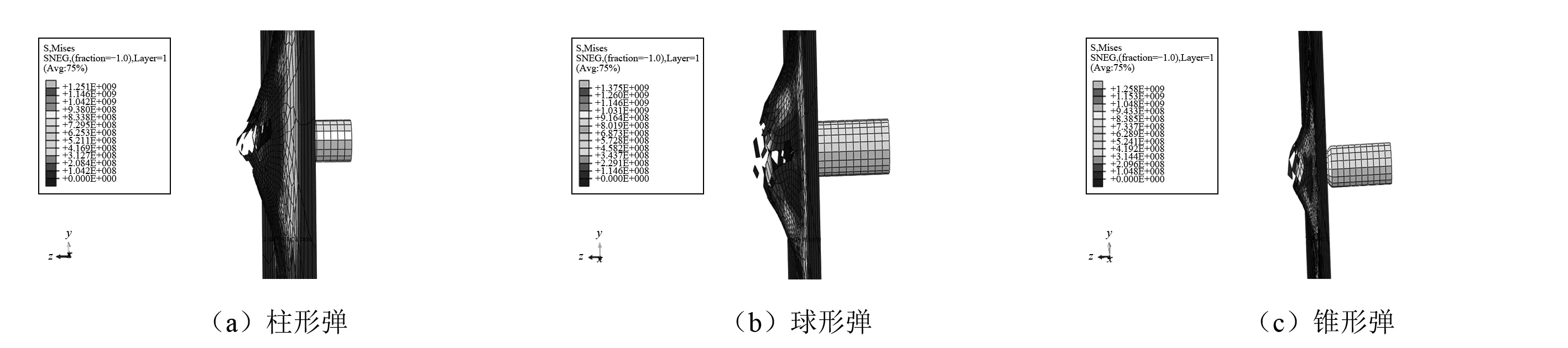
图10 层合板被不同形状弹体击穿瞬间破坏侧视图Fig.10 The side view of laminates in the moment of breakdown by different projectile

3 结 论

通过对不同形状弹体正冲击芳纶纤维层合板的有限元计算分析，可以得到如下结论：

(1)子弹完全穿透层合板的临界速度和弹头的形状有关，锥形弹的临界速度最小，柱形弹的临界速度最大，球形弹的临界速度介于二者之间。

(2)三种形状弹体的剩余速度均随初始速度的增大而增大，在相同的初始速度下，柱形弹体的动能变化最大，球形弹体次之，锥形弹体的动能变化最小，可见不同形状的弹体杀伤力不同。

(3)三种形状弹体以临界速度正冲击层合板时，柱形弹体穿透后层合板的破坏呈菱形，即规则的四边形，而球形弹体和锥形弹体的破坏分别呈现不规则圆形和相对较规则圆形，板的四周能看到轻微的断裂失效。

(4)层合板的破坏机制与弹头的形状也有很大关系，柱形弹体在穿透层合板时相对较钝，层合板被拉伸的较为明显，板的破坏趋于背面纤维拉伸失效；而球形弹体和锥形弹体在穿透层合板时，板的突起相对较小，板的破坏趋于正面基体发生压缩失效产生剪切破坏。

(5)层合板的破坏面积与弹头的初始速度有关，较低速度时层合板破坏面积较小而规则，在较高速度下层合板的破坏面积较大且趋向不规则。

[ 1 ] 陈磊，徐志伟，李嘉禄，等. 防弹复合材料结构及其防弹机理[J]. 材料工程，2010 (11): 94-100.

CHEN Lei, XU Zhiwei, LI Jialu, et al. Structure and bullet-proof mechanism of ballistic composites [J]. Journal of Materials Engineering, 2010 (11): 94-100.

[ 2 ] BUDIGER H. Ballistic protective fabrics-past and future [C]∥Proceedings of the 34th International SAMPE Technical Conference. Baltimore: SAMPE， 2002： 499-505.

[ 3 ] KASANO H. Recent advance in high-velocity impact perforation of fiber composite laminates [J]. Jsme International Journal, 1999，42(2): 147-157.

[ 4 ] HEARLE J W S, LEECH C M. Ballistic impact resistance of multi-layer textile fabrics：AD-A128064 [R]. England: University of Manchester Inst. of Science and Technology, 1983.

[ 5 ] 周传雷. 我国芳纶产业发展现状[J]. 化学工程师, 2010, (12): 47-49.

ZHOU Chuanlei. Domestic development status of aramid fiber industry [J]. Chemical Engineer, 2010 (12): 47-49.

[ 6 ] 钱伯章.芳纶的国内外发展现状[J].化工新型材料,2007, 35(8): 26-27.

QIAN Bozhang. Current developing situation of aramid fiber at home and abroad [J]. New Chemical Materials, 2007, 35(8): 26-27.

[ 7 ] 秦建兵,韩志军,刘云雁, 等. 复合材料层合板侵彻行为的研究[J]. 振动与冲击, 2013,32(24)：122-126.

QIN Jianbing, HAN Zhijun, LIU Yunyan, et al. Penetration behavior of composite laminated plates [J]. Journal of Vibration and Shock, 2013, 32(24): 122-126.

[ 8 ] LOPEZPUENTE J, ZAERA R, NAVARRO C. Experimental and numerical analysis of normal and oblique ballistic impacts on thin carbon/epoxy woven laminates [J].Composites Part A-Applied Science and Manufacturing, 2008, 39(2): 374-387.

[ 9 ] TAN V B C, LIM C T, CHEONG C H. Perforation of high-strengh fabric by projectiles of different geometry [J]. International Journal of Impact Engineering, 2003, 28(2): 207-222.

[10] 马小敏.芳纶纤维层合板的冲击动力学行为[D].太原:太原理工大学，2015.

[11] 王元博,王肖钧,胡秀章,等. Kevlar层合材料抗弹性能研究[J].工程力学,2005,22(3): 76-81.