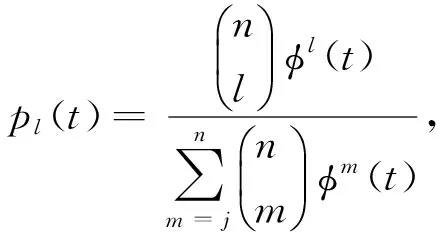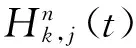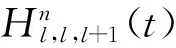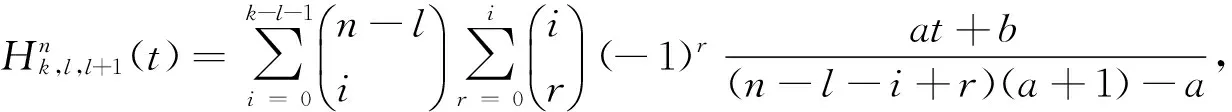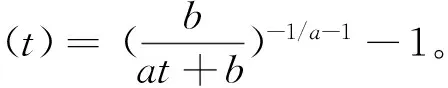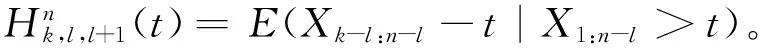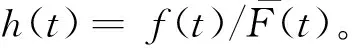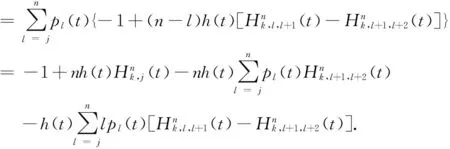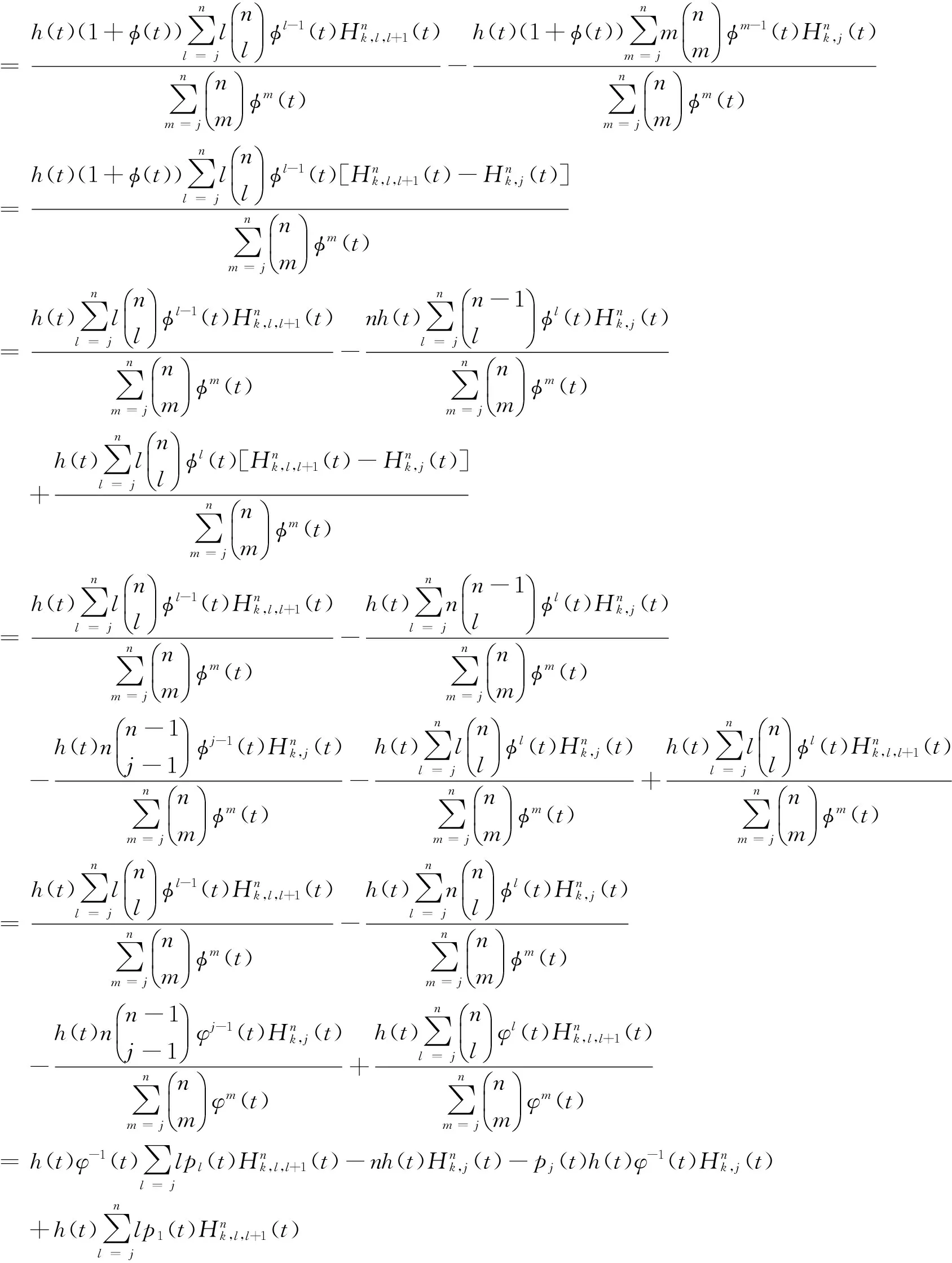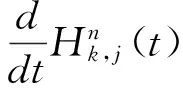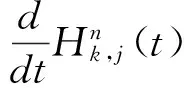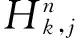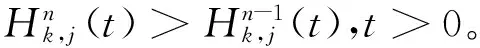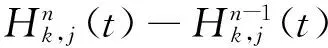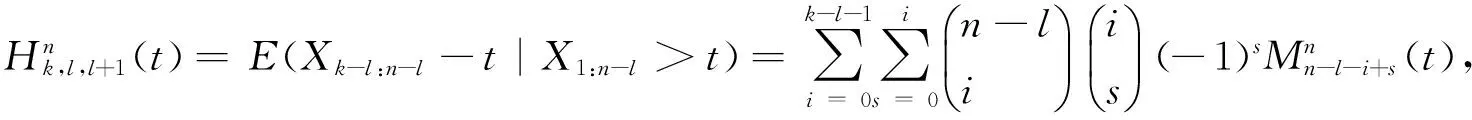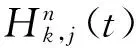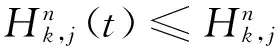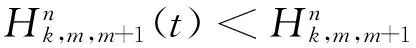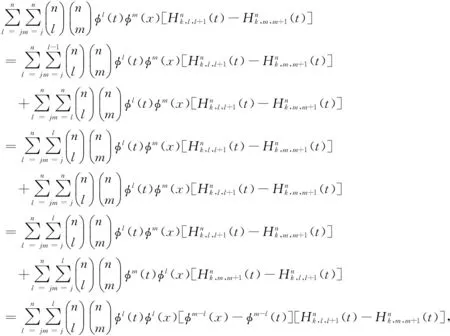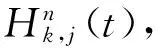n取(n-k+1)系统条件平均剩余寿命的一些性质
2018-03-23温九红张正成强玉霞
温九红, 张正成, 强玉霞
(兰州交通大学 数理学院,甘肃 兰州 730070)
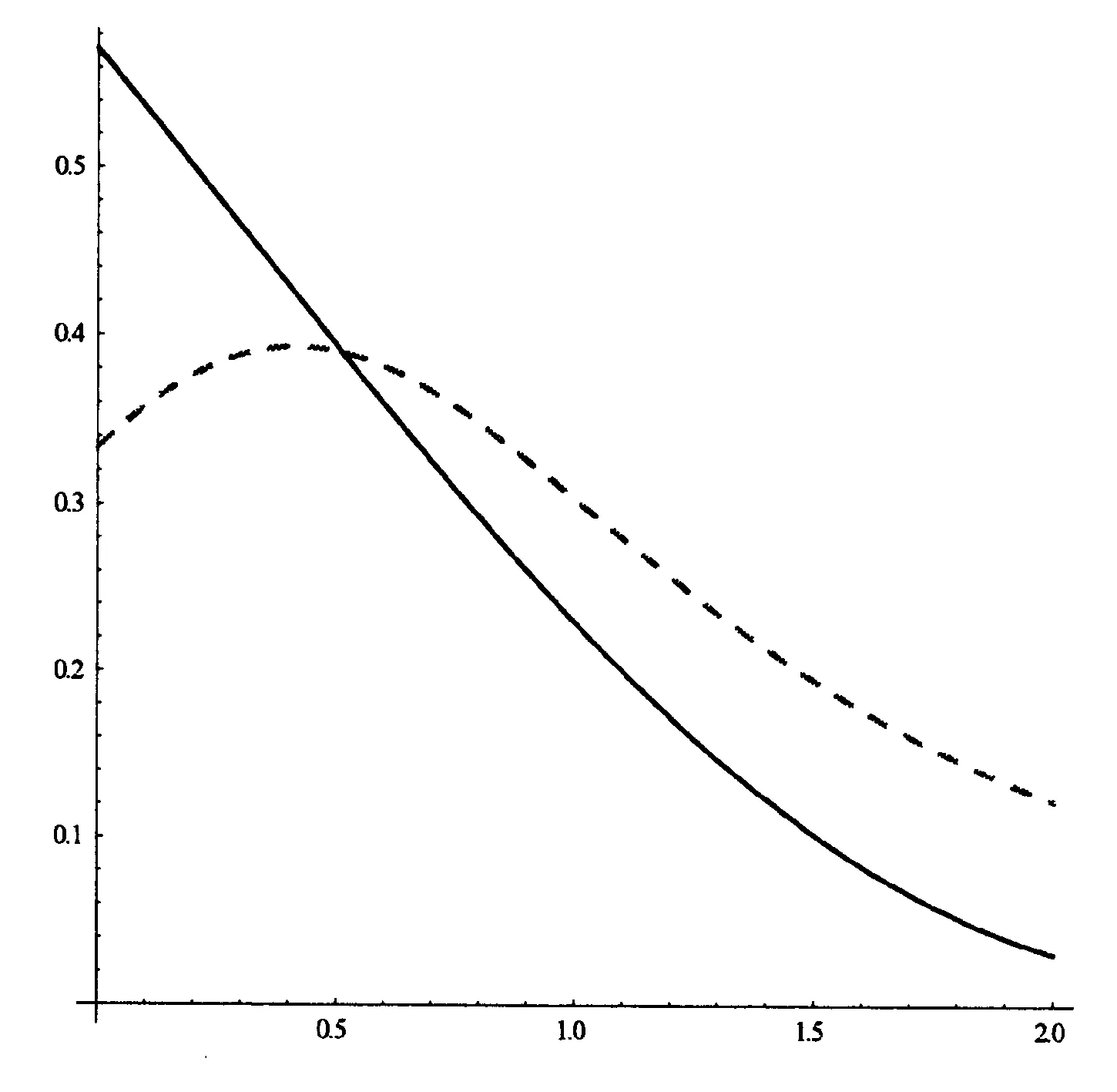
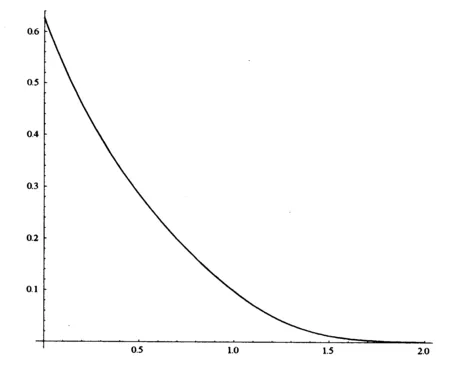
所谓n取(n-k+1)系统是指有n个元件构成的系统中,系统要正常工作当且仅当至少有n-k+1个元件正常工作。设X1,X2,…,Xn为n个独立同分布的元件寿命,其构成的系统的寿命记为T,X1:n,X2:n,…,Xnn为X1,X2,…,Xn对应的由小到大排列的顺序统计量,则Xkn恰好为n取(n-k+1)系统的寿命。在可靠性理论和生存理论中,系统的剩余寿命问题是一类特别重要的问题,在过去的几十年中,已经有许多学者对其做了大量研究,例如Asadi[5]研究了由n个独立同分布元件构成的n取n-k+1系统在时刻t没有元件失效的平均剩余寿命,即E(Xk:n-t|X1:n>t);Li[7]等研究了n中取(n-k+1)系统在时刻t失效的元件不大于l(1≤l (X-t|X>t)。 对任意的x>0,其可靠性函数为 那么,平均剩余寿命为 定义1X称之为IFR(失效率递增),如果其失效率 关于t≥0递增。 R(x|t)=P(Xk:n-t>x|Xj:n (1) (2) 例1 令X1,X2,…,Xn相互独立且同分布于一般Pareto分布,其可靠函数为 图1 例1中的平均剩余寿命函数 因此根据(1)式有 定理1假设n中取(n-k+1)系统中的元件都有绝对连续的分布函数F且分布函数F在(0,∞)严格递增,则分布函数F可以表示为 证明对(1)式的两边分别对t求导则有 (3) 其中pl(t)在定理1中已给出。根据Goliforushani和Balakrishnan(2012)[8]有 根据Asadi 和Bayramoglu(2006)[3]可知 1003 大动脉粥样硬化与心源性栓塞大脑中动脉 M1 段闭塞急性缺血性脑卒中血管内治疗单中心回顾性分析 常晓赞,张 磊,李子付,许 奕,黄清海,刘建民,杨鹏飞,洪 波 另一方面 把A和B带入(3)式中得到 其中φ-1(t)lpl(t)-(n-l+1)pl-1(t)=0,因此 这也蕴含着 经过一些计算后得到 等价于 (4) 其中(4)式中的第一部分等于0,现只需证明(4)式中第二部分小于等于0即可。 根据Asadi 和Bayramoglu(2006)[3]可知E(Xk:n-t|X1:n>t)>E(Xk-1:n-1-t|X1:n-1>t),因此当j≤l时有E(Xk-l:n-l-t|X1:n-l>t)≥E(Xk-j:n-j-t|X1:n-j>t)。故(4)式中的第二部分为负,得证。 证明根据(1)式有 图2 例2中的平均剩余寿命函数 (5) (6) 例2 令n中取n-k+1系统中的元件服从韦伯尔分布,其可靠函数为 当α=2,β=1时r(t)=2t,显然r(t)关于t单调递增。根据(1)式有 [1] 曹晋华,程侃.可靠性数学引论[M].北京:高等教育出版社,2006. [2] 程侃.寿命分布类与可靠性数学理论[M].北京:科学出版社,1999. [3] ASADI M, BAYRAMOGLU I. The mean residual life function of ak-out-of-nstructure at the system level[J]. IEEE Transaction on Reliability, 2006(55):314-318. [4] TAVANGAR M, BAIRAMOV I. On conditional residual lifetime and conditional inactivity time ofk-out-of-nsystems[J]. Reliability Engineering and System Safety, 2015(144):225-233. [5] ASADI M. On the mean past lifetime of the components of a parallel system[J]. Journal of Statistical Planning and Inference, 2006(136):1197-1206. [6] TAVANGAR M, ASADI M. The study on the mean past lifetime of the components of (n-k+1)-out-of-nsystem at the system level[J]. Metrika, 2010(72):59-73. [7] LI X, ZHAO P. Some aging properties of the residual life ofk-out-of-nsystems[J]. IEEE Transaction on Reliability, 2006(3):535-541. [8] GOLIFORUSHANI?S, BALAKRISHNAN N. On the residual and inactivity times of the components of used coherent systems[J]. Journal of Applied Probability, 2012,49(2):385-404.1 相关概念和定义
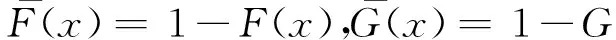
2 主要结论