深入理解失效率和返修率∗
2019-07-31张德晶冯兴乐王孟婕
张德晶 冯兴乐 王孟婕
(长安大学信息工程学院 西安 710064)
1 引言
失效率是可靠性工程中一个重要的参数,深入理解这个参数的概念对可靠性的学习具有重要意义。然而在可靠性领域,对这个参数的理解还较为模糊,导致了许多人无法将可靠性参数与工程应用联系起来。因此本文通过论述失效率与返修率及平均无故障时间(Meantime Between Failures,MTBF)与返修率的关系,将这个可靠性参数与市场层面的返修率联系起来。并通过简单的公式推导,论述了瞬时失效率、平均失效率及返修率的本质含义。
文中涉及的各种实例,目的是让读者能更清晰的理解各参数的内在含义,在实际应用场景中并不一定适用。
2 失效率
2.1 失效率与单位时间
失效率指的是在某时刻尚未发生故障的产品在该时刻后单位时间内发生失效的概率[9]。但是失效率有多种表现形式,区别在于单位时间不同。
按照国际量纲,单位时间单位为秒,失效率是每一秒钟的失效比例。但一方面,1s的时间不足以有效观察失效状态,因此,将单位时间扩展为1h,且假设在1h 内,产品的各种失效参数不变,因此,业界常用失效率(10-nh)来表示元器件产品的可靠性,即元器件工作1h内的失效率。
另一方面,由于电子产品的失效率很低,若采用少量样本,在一小时内,可能1 例失效都没有,为了观察到至少1例失效,需要大量的样本。
在可靠性工程中,失效率的单位是菲特(FIT),表示每十亿产品小时内的失效数。“产品小时”指产品数量和观测时间的乘积。上述分析表明:由于电子产品的失效率很低,为了得到较为准确的失效率,需要样本数*试验时间较大,样本数和试验时间可以互换。但前提是在此间隔内,失效率为常数。
例如,对于失效率很低的钽电容,若采用1h 的试验时间,需要庞大的不能接受的样本数,但钽电容的单价较高,不能无限地增加样本数,且钽电容的失效参数较稳定,因此,通常标准的测试时间为1000hrs,这就是为什么钽电容的基础失效率以0.5%/1000hrs 来表示,而并不是用5*10-6/hrs 表示。这就是通过扩展时间间隔,降低所需样本数。
2.2 平均失效率与瞬时失效率[1~2]
回顾一下美军标338,定义失效率 λ(t)为t1~t2时间间隔(Δt)内发生故障的概率,并假设时刻t1之前未发生失效。计算公式如下:

该失效率即为平均失效率,需要注意的一点是在t1 时刻之前没有发生故障,即可靠度R(t1)始终是从1开始的。
假设用N0台设备进行试验,在某时刻t,产品失效了r(t),有Ns个产品仍然完好。则任意时刻t的可靠度R(t)为

将R(t)带入失效率式(1)可得:

瞬时失效率指的是每一时刻的失效率,在实际工程中我们无法测量某一时刻,严格意义上的瞬时失效率不存在,只能说是很短的一个时间段的失效率。具体来讲,先求一段时间内的平均失效率,然后让时间间隔趋向于零,即Δt 趋向于0,可得:

根据不可靠度F(t)与可靠度R(t)的关系,可得到:

根据失效密度函数的公式可以得到:

瞬时失效率的另一公式为

该公式与式(3)没有太大区别,式(3)指的是第一个失效区间,即在时刻t 之前未发生失效。
由此关系式我们可以得到,失效率h(t)是以失效密度函数 f(t)为求解基础的,可靠度增大失效率降低。
下面由一个例子来具体说明。
抽取80 个样品进行寿命试验,失效时间和相应的失效数量整理见下表,共有8 个试验时间区间,每个区间为400h。

表1 各时间段产品失效数
解:失效密度函数的公式为

瞬时失效率的计算公式为

平均失效率的公式为

将数值带入可得
f1(400)=3/(80×400)=9.38×10-5f2(400)=18/(80×400)=5.63×10-4……
f7(400)=2/(80×400)=6.25×10-5f8(400)=1/(80×400)=3.13×10-5瞬时失效率:
λ(400)=3/(80×400)=9.38×10-5λ(800)=18/(77×400)=5.84×10-4……
λ(2800)=2/(3×400)=1.67×10-3λ(3200)=1/(1×400)=2.5×10-3
平均失效率:
m(400)=3/(400×80)=9.38×10-5m(800)=21/(800×80)=3.28×10-4……
m(2800)=79/2 800×80=3.52×10-5
m(3200)=80/3 200×80=3.13×10-4
由此可见,t=0 时刻开始的首个试验区间,失效率λ(t)和失效密度f(t)的计算结果是一致的。瞬时失效率是在单位时间内失效产品在剩余产品中所占比例,而失效密度是在单位时间内,失效产品在总产品中所占比例,因此无论区间范围如何选择,同一区间的瞬时值(瞬时失效率)必大于区间平均值(失效密度)。平均失效率和瞬时失效率没有本质上的区别,只要选取的时间区间不影响观察结果即可,因此严格意义上来说没有瞬时失效率。
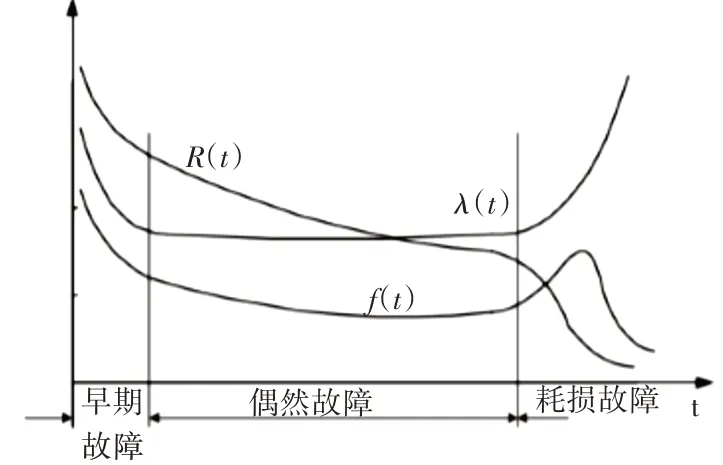
图1 故障率、可靠度和密度函数曲线
由图1 可直观地反应失效密度函数在耗损期先增大后减小,这是因为在耗损期的早期产品失效数骤增,失效密度函数急剧增大,而在耗损期后期,未失效产品所剩无几,失效个数减少,失效密度函数减小。
相反,平均失效率的另一公式为

当产品寿命服从指数分布的时候,平均失效率与瞬时失效率是相等的,即λ(t)=λ,这是因为当产品寿命服从指数分布时其失效率为一常数,可得:
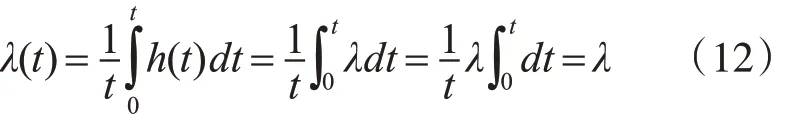
由于除指数分布外的其他分布的失效率λ为t的函数,因此严格意义上来说,每一刻的失效率并不是固定不变的,这样不便于实际工程的应用,因此,在实际工程中经常用平均失效率。
3 返修率
3.1 返修率与失效率的关系
对于已投入市场的定型产品,通常使用售后服务部门提供的返修率表示产品的故障比例和产品质量,这里的年返修率就是单位时间为一年的平均失效率,而不关心其具体失效时刻。年返修率=一年内返修的产品个数/投入市场的总产品数。
由此可见,返修率反应的是产品的失效比例,而失效率是表示元件或系统下一时间失效的概率,二者没有必然联系,但若是产品不间断的连续工作,年返修率即为一年内失效率的累积。
下面由一个例子来说明。
500个样品同时进行2000h的测试,发现失效2个,假设该产品一直处于偶然失效期,且服从指数分布。预计每个该产品投入市场,且无间断运行3年的返修个数。
解:由所给条件:
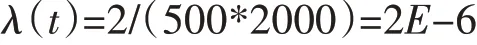
那么这批样品“每一个”运行3 年的返修个数是为:

上述例子只是为了说明了理论上连续工作的产品的返修率与瞬时失效率的关系,但在实际工程中,返修率是建立在大样本条件下的,无法具体到每个产品,且实际外界环境与实验环境存在一定的差异,所以预计值与实际值存在一定差异。
3.2 返修率与MTBF的关系[3~4]
为了体现可修复产品的时间质量,经常用平均无故障间隔时间(Meantime Between Failures,MTBF)来描述产品在规定时间内保持功能的能力[13]。在不考虑存储和闲置时间的情况下,年返修率=(1/MTBF)*365*24。
因此,预计一个产品的MTBF 是为了告诉用户该产品可用多少年不出故障,并可由此预计产品年返修率。显然,在实际工程中产品一般都是不连续工作,这就导致返修率预计值一般大于实际值。
需要指出的是,利用MTBF 值预计年返修率需要考虑产品是否连续工作,例如:某种产品100 个,每天工作24h,一年中坏了5个,如果按实际工作时间来算,MTBF=24*365*100/5。另外一种产品100个,每天工作12h,一年中坏了5 个,按实际工作时间来算,MTBF=12*365*100/5。明显两种产品的返修率一样,但MTBF却不一样。
因此MTBF 的预计有时也需要考虑是否连续运行的情况,有的MTBF 通过连续运行,得出失效率计算得到;有的MTBF 需要通过模拟实际运行(比如4h 运行,4h 闲置),得出失效率计算得出(一般要分别计算运行状态和非运行状态的MTBF)。比如说开关,正常连续通电基本不会坏,有相关的标准会指定它连续通电多少小时就算可靠;开关最主要的性能是通断,通断寿命是其主要的性能,因此,其MTBF 就不按小时来计算,而是按通断次数来算,那么计算MTBF 多少次的时候,可能就5s 通电5s断电来计算。
下面通过一个例子来理解MTBF。
对于一可修复产品,其MTBF=5 年(43800h)。我们可以将其理解为
1)每个这样的产品的工作时间达到43800h 的概率为
P=e-t/MTBF 当t=MTBF
=e-1
=0.3677 or 36.8%
2)若在市场中投入100 个产品,则每个产品的MTBF 为438h,也可以理解为100 个产品不出现故障所能维持的时间为438hr,438hr后就会有个别产品出现故障,43800hr 后有63.2%(1-36.8%)的产品会发生一次或多次故障。
3)该产品的年平均故障率为20%(产品返修后继续投入市场,5 年后每个产品的故障次数可能为多次)。
4)但是我们不能说该产品的寿命为5 年或该产品在五年内不发生故障。
由此可见,产品运行时间超出预计的MTBF 值后,还有36.8%的产品完好,其失效率不变,除非其寿命达到耗损期。例如,对于指数分布的产品,MTBF为10年意思就是累积用10年坏1个,每年有十分之一的产品会坏,运行时间超过十年就是说每年少于十分之一的产品会坏。
4 结语
在可靠性基本知识的学习中,大部分人都无法将失效率的概念联系到实际应用。本文通过论述失效率,返修率及MTBF 三者的关系,将技术层面的可靠性参数与市场层面的返修率联系起来,以期读者能更清晰地理解这几个参数的实际含义。
