拉格朗日力学逆问题和量纲分析
2018-03-23丁光涛
丁光涛
(安徽师范大学 物理与电子信息学院,安徽 芜湖 24100)
引 言
拉格朗日力学逆问题研究力学系统的运动微分方程能否表示成为拉格朗日方程形式,或者说,能否从哈密顿变分原理导出,这种研究开拓了传统分析力学的研究领域,将一些非保守系统纳入了拉格朗日系统;突破了传统的拉格朗日函数框架,提出非标准拉格朗日函数的概念。分析力学自身也因逆问题研究而产生新的课题,如非保守系统的正则化问题,拉格朗日函数的等效性问题,进而在物理学中也推动了新课题的研究,如耗散系统的量子化问题,场论中的逆问题等。这种逆问题研究的进展推动了应用分析力学理论和方法来处理微分方程问题,而在当代自然科学和社会科学中建立以微分方程模型为代表的数学模型,是普遍应用的重要研究方法,因此,逆问题的成果可以也应当应用到许多不同的学科研究中[1-6]。逆问题研究中一个重要方面是拉格朗日函数的构造方法,这个方面已经取得很多的成果,值得强调的是许多方法与微分方程的第一积分相关[7-11]。
通常将拉格朗日力学逆问题称为变分法逆问题,两者不加区别,这反映逆问题研究中的一种普遍倾向,即重视问题的数学方面,而忽视其物理方面,其实应当重视拉格朗日力学逆问题研究中的物理意义,它不是纯粹的数学问题。本文以谐振子和线性阻尼振子为例来说明上述观点,为了使讨论简单明晰,下面只以量纲来代表问题的物理方面,第一节给出量纲理论的简要回顾[12,13];第二节给出谐振子运动方程、第一积分,以及相应的拉格朗日函数和哈密顿函数,并讨论相关的量纲问题;第三节讨论线性阻尼振子的对应问题;第四节是小结和讨论。
1 量纲及其法则要点
物理学中存在诸多不同的物理量,可以分成基本量和导出量,在确定了单位制后,一个导出量能够用若干个基本量的乘方之积表示出来,这个表达式称为该物理量的量纲式。量纲是物理学中的一个重要问题,可以表征物理量的性质(类别),如力学中的时间、长度、质量、动量、能量等。量纲分析是物理科学中一种重要的研究方法,它根据一切量所必须具有的形式来分析判断事物间数量关系所遵循的一般规律,简而言之,就是可以在量纲法则的原则下,分析和探求物理量之间关系。通过量纲分析可以检查反映物理现象规律的方程在计量方面是否正确,甚至可提供寻找物理现象某些规律的线索,以指导在物理领域中建立数学模型或进行实验。基本的量纲法则有两条:1.只有量纲相同的物理量,才能彼此相加、相减和相等;2.指数函数、对数函数和三角函数的宗量量纲应当为1。量纲法则是量纲分析的基础, 对力学和物理学问题,若导出的公式不符合量纲法则,该式必然是错误的。下面从基本的量纲法则出发,讨论拉格朗日力学逆问题的物理意义,而且讨论局限于力学范围内,基本量仅有时间、长度和质量。
2 谐振子第一积分和拉格朗日函数的量纲分析
质量m的小球和倔强系数k的弹簧构成的谐振子,其运动微分方程为
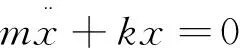
(1)
通常将上述方程改写为
(2)
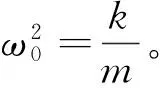
(3)
与之对应的拉格朗日函数是
(4)
从数学上,还可以构造其它积分,包括与时间无关的积分,如
(5)
下面利用文献[15]中钱德拉塞卡等提出的方法,从I2构造振子的拉格朗日函数。设对应的拉格朗日函数为L2,由于I2与时间无关,直接取作雅可比积分,即存在如下关系式
(6)
进而导出
解出p2后,代入式(6),即得到待求的拉格朗日函数
(7)
文献[18]对这种方法进行了研究,说明其理论基础是诺特定理的逆问题,同时指出这种方法存在局限性。对式(6)I2进行上述程序的运算后,得到
(8)
(9)
上面谐振子的两个拉格朗日函数,如果从物理意义方面分析,例如,从基本的量纲法则分析,则可以表明第一个解是符合量纲法则的,I1和L1的量纲是能量量纲,L1是标准形式的拉格朗日函数,它对时间积分的量纲是作用量量纲。但是,第二个解在物理上是存在问题的,首先,I2表达式不符合量纲法则,对数函数的宗量量纲不是1,即不是无量纲的,而是具有能量量纲;p2的量纲不是通常的力学动量量纲;L2是非标准形式的拉格朗日函数,其表达式前一项量纲为1的纯数,而后一项是能量量纲宗量的对数,它对时间的积分不具有力学(物理学)作用量的量纲,这就是说,在传统的力学(物理学)意义上,第二个解是不符合要求的。
根据第一个解,谐振子哈密顿函数为
(10)
在此基础上,可以进一步讨论谐振子量子化。但是,根据第二个解,导出的谐振子的哈密顿函数为
(11)
显然,它不符合量纲法则,也不可能由此讨论系统的量子化。
3 线性阻尼振子第一积分和拉格朗日函数的量纲分析
考虑存在阻尼的情况,一维线性阻尼振子的运动微分方程为
(12)
可以得到振子的两个积分[15-17]
(13)
(14)
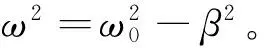
(15)
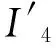
从积分I3和I4构造出对应的拉格朗日函数分别是
(16)
(17)
从方程(12)可确定β,ω0以及ω的量纲都是[T-1],显然,积分I3和拉格朗日函数L3的表达式都是符合量纲法则的,它们的量纲与能量量纲相同(m=1)。但是,积分I4和拉格朗日函数L4的表达式不符合量纲法则,这两个表达式中一项是量纲为1的纯数,另一项是对数函数,其宗量却具有能量量纲。L3是标准形式的拉格朗日函数,对应的哈密顿函数为
(18)
式中广义动量为
(19)
L4是非标准形式的拉格朗日函数,对应的哈密顿函数和广义动量为
H4=-ln[ωxsec(ωxp4)]+βxp4
(20)
(21)
显然,H4的表达式不符合量纲法则,p2量纲也与标准的动量量纲不同。讨论阻尼振子的量子化,可以从式(18)出发,却不能从式(20)出发。但是应该指出,这种不符合物理法则的结果,在数学上仍然是有用的,文献[15]表明从这种形式的哈密顿函数出发,利用分析力学的理论和方法,能够得到方程(12)的解。
4 结束语
上面以谐振子和线性阻尼振子为例,讨论了从运动方程到运动积分,再到拉格朗日函数和哈密顿函数,这样的求解逆问题过程。值得注意的是,如果仅从数学方面来考虑,将上述谐振子方程(2)和线性阻尼振子方程(12)看作纯粹的微分方程,那么上面导出的第一积分、拉格朗日函数、哈密顿函数、动量的数学表达式等等都是容许的,不仅能够利用这样的拉格朗日函数和哈密顿函数导出运动微分方程,而且利用分析力学的方法能够得到方程的解,事实上这种方法已经推广到求解更为复杂的微分方程[15,19]。但是,从力学(物理学)方面来看,所有数学表达式,无论是定义式,还是方程式,其中出现的量都应当有确切的物理意义,这些数学表达式都应当遵循一般的物理规律。量纲法则是超越具体物理过程的基本物理规律,适合利用这个法则来检验讨论中的数学表达式,检验的结果表明有些表达式是违背量纲法则的,上面指出从这种结果不具有物理意义,不能讨论量子化问题。
我们认为,对于讨论逆问题时出现的数学方法与物理意义之间的矛盾应当重视,在处理力学(物理学)问题时,不能轻易突破物理规律的制约,而是应当在利用数学方法导出的结果中,有所鉴别和选择,或者说,在运用多种不同的数学方法处理实际力学(物理学)问题时,必须重视物理意义的分析和物理规律的论证,即使在用数学方法处理实际力学(物理学)问题时,不能每一步都满足物理规律,不能每一个数学表达式都具有确定的物理意义,但最后结果却要回到力学(物理学)上来。
根据上述分析,我们认为通常将拉格朗日力学逆问题等同于变分法逆问题的看法值得商榷,这两种逆问题提法实质上是存在区别的,前者是物理学(力学)中的理论和方法,必须同时遵循数学规律和物理规律,而后者是数学中的理论和方法,只需要遵循数学规律,不必讨论其物理意义;换句话说,前者是后者的一部分。最后指出,除了逆问题研究外,在力学研究中还存在着其它数学方法与物理意义相悖的问题,我们都应当进一步讨论。
[1] SANTILLI R M. Foundations of theoretical mechanics I[M]. New York: Springer-Verlag,1978.
[2] SANTILLI R M. Foundations of theoretical mechanics II[M]. New York: Springer-Verlag,1983.
[3] 梅凤翔.分析力学专题[M].北京:北京工业学院出版社,1988.
[4] SAUNDERS D J. Thirty years of the inverse problem in the calculus of variations[J]. Reports on Mathematical Physics, 2010(66):43-53.
[5] LOPUSZANSKI J. The inverse variational problem in classical mechanics[M]. Singapore: World Scientific, 1999.
[6] 丁光涛.理论力学[M].合肥:中国科学技术大学出版社,2014.
[7] MUSIELAK Z E. Standard and non-standard Lagrangians for disspative dynamical systems with variable coefficient[J]. J Phys A:Math Theor, 2008(41):055205.
[9] SARLET W. Symmetries, first integrals and the inverse problem of Lagrangian mechanics[J]. J Phys A:Math Gen, 1981(14):2227-2238.
[10] 丁光涛.从第一积分构造Lagrange函数的直接方法[J].动力学与控制学报,2011,9(2):102-106.
[11] 丁光涛.变分法逆问题研究的若干进展[J].北京大学学报(自然科学版),2016,52(4):732-740.
[12] 谈庆明.量纲分析[M].合肥:中国科学技术大学出版社,2005.
[13] 包科达.中国大百科全书(物理学)词条:量纲和量纲分析[M].北京:中国大百科全书出版社,1987.
[14] 丁光涛.关于谐振子第一积分的研究[J].物理学报,2013,62(6):064502.
[15] CHANDRASEKAR V K. SENTHIVELAN M, LAKSHMANAN M. On the Lagrangian and Hamiltonian description of the damped linear harmonic oscillator[J]. J Math Phys, 2007(48):032701.
[16] 丁光涛.关于线性阻尼振子第一积分的研究[J].物理学报,2013,62(6):064501.
[17] 丁光涛.阻尼谐振子的拉格朗日函数和哈密尔顿函数[J].大学物理,2009,28(3):13-14.
[18] 丁光涛.关于钱德拉塞卡构造拉格朗日函数方法的若干问题[J].安徽师范大学学报(自然科学版),2017,40(1):1-6.
[19] CHANDRASEKAR V K, SENTHIVELAN M, LAKSHMANAN M. On the general solution for the modified Emden-type equation[J]. J Phys A: Math Theor, 2007(40):4717.
