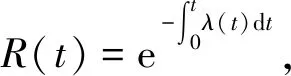基于改进龙格-库塔法反舰导弹贮存寿命研究
2019-05-23谢春思
李 强,谢春思,盖 强,吴 帅
(海军大连舰艇学院,辽宁 大连 116018)
0 引 言
可靠性是产品在使用时间内不发生故障的性质[1]。对数正态分布在可靠性工程中是一种重要的寿命分布,常用于描述产品的耐磨寿命与疲劳寿命[2],广泛应用于半导体器件的寿命实验、加速寿命实验、电子设备的平均维修时间和电子元器件的可靠性增长过程[3-4]。
长期不工作或不使用的状态通常称为非工作状态(包括库房贮存、运输、战备值班等),也称为贮存状态。反舰导弹具有“长期贮存、一次使用”[5]的特点,导弹从发射到击中目标,工作时间较短,绝大部分时间都处于贮存状态,对于具有高可靠度的反舰导弹,贮存寿命直接影响其可靠性。因此,研究反舰导弹的贮存寿命,提高反舰导弹的可靠性具有现实意义。
在可靠性工程中,失效率作为可靠性特征量具有重要的意义。通常情况下,产品失效率是时间的函数,失效率函数曲线一般呈浴盆状,分为3个阶段:早期失效期、偶然失效期和耗损失效期,例如指数分布的失效率函数为常数,威布尔分布则能全面地描述浴盆曲线的各个阶段,正态分布的失效率函数随时间增长呈递增趋势。因此问题随之而来,对于任意分布的失效率函数是否满足浴盆曲线值得研究,而对数正态分布函数正是一个例外,随着产品使用时间的增长,它的失效率并不符合浴盆曲线,有文献称之为“倒浴盆”形[6],文献[6]从理论上证明了对数正态分布失效率函数的单调性。本文通过龙格-库塔法,运用Matlab进行数值仿真得到其失效率函数曲线,分析曲线变化趋势,得到失效率的渐近值。
1 对数正态分布失效率函数
设随机变量t的自然对数lnt服从均值为μ和标准差为σ的正态分布,则此对数正态分布失效概率密度函数f(t),累积失效概率函数F(t),可靠度函数R(t),这些特征量可表示为[7]:
(1)
(2)
(3)
由失效概率密度函数f(t)、可靠度函数R(t)与失效率函数λ(t)三者关系可知故障率为:
(4)
2 反舰导弹可靠度的龙格-库塔法仿真
龙格-库塔法常用于微分方程的数值计算,是一种在工程上应用广泛的高精度单步算法。龙格-库塔法的理论基础来源于泰勒公式和使用斜率近似表达微分,利用在积分区间内多预估几个点的斜率,进行加权平均,以此为平均斜率的近似值,抑制误差,从而构造出精度更高的数值积分[8]。
由于龙格-库塔法利用数值积分求解积分域0~t的微分方程,而可靠度R(t)的积分域为t~∞,为了使其满足龙格-库塔法使用条件,通过累积失效概率函数与可靠度函数的关系式:
R(t)=1-F(t)
(5)
首先构造微分方程:
(6)
式中:均值μ和标准差σ均为给定常数。
取步长h为0.001,由龙格-库塔法[9]:
(7)
(8)

(9)
(10)
(11)
由式(3)、(4)、(5),通过Matlab对可靠度函数R(t)与失效率函数λ(t)进行仿真,仿真结果如图1~图4所示。

图1 当μ=0.5时,对数正态分布可靠度函数图
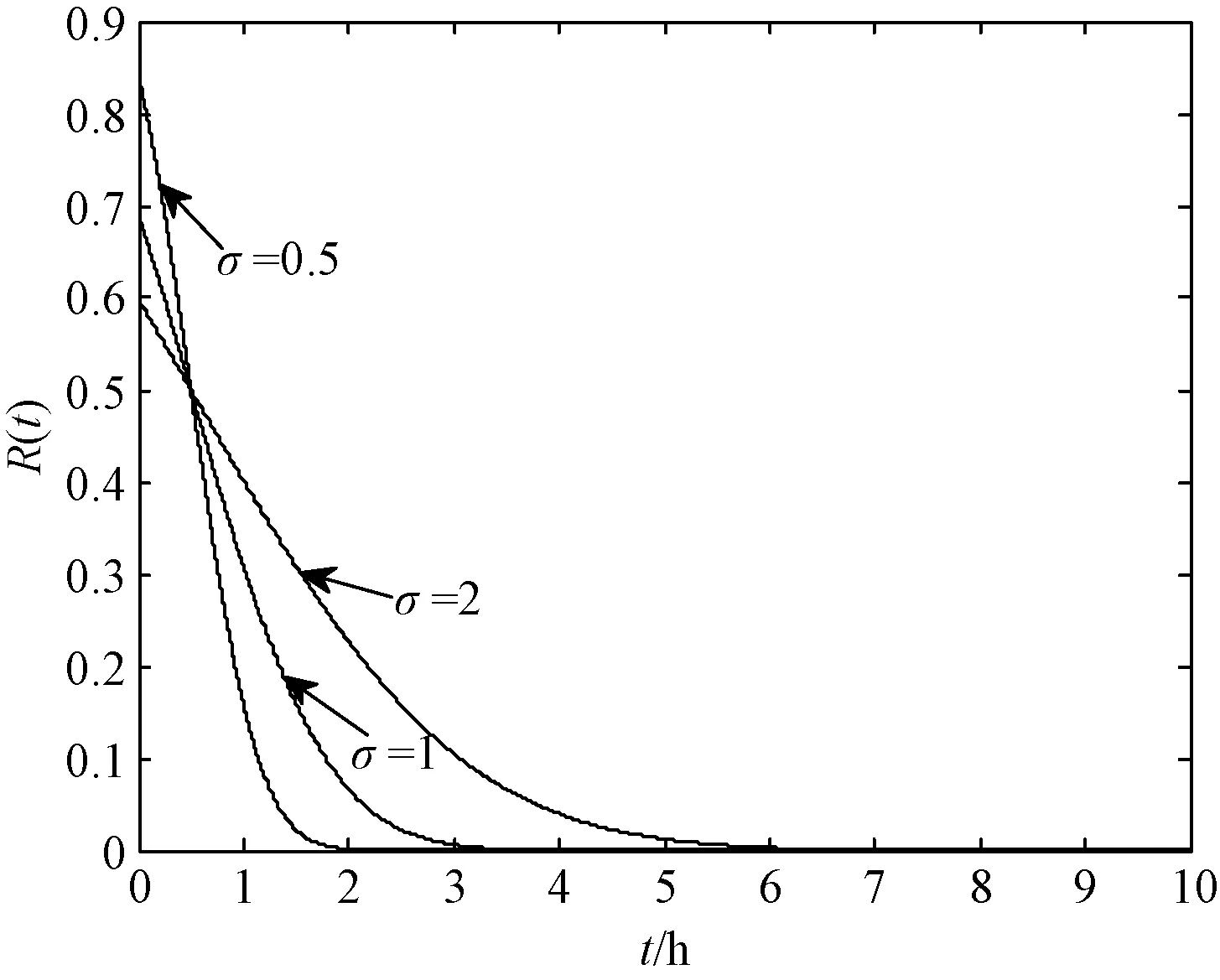
图2 当μ=0.5时,正态分布可靠度函数图
由图1和图2可知,当均值μ=0.5时,对数正态分布与正态分布的可靠度函数均在短时间内降低,呈递减趋势,通过延长仿真时间,可靠度函数最终趋于零。对数正态分布函数的可靠度明显高于正态分布函数的可靠度,对于反舰导弹的寿命,自然环境和人为因素影响其均值大小,从而影响其可靠度,在可靠度高于0.5的范围内,标准差越小,寿命的可靠度随时间下降速率减缓。

图3 当μ=0.5时,对数正态分布失效率函数图

图4 当μ=0.5时,正态分布失效率函数图
由图3知,当均值μ=0.5时,对数正态分布的失效率函数在短时间内随时间迅速增大,达到最大值,然后呈递减趋势,通过延长仿真时间,失效率函数最终趋于零。由图4知,当均值μ=0.5时,正态分布的失效率函数表现为随时间增加呈递增趋势。通过比较对数正态分布与正态分布失效率函数图,得到了不同失效机理对应的失效率函数,对于反舰导弹的寿命,标准差对其失效率影响较大,尽管当贮存寿命的标准差较小时,它有较低的失效率,但在短时间内失效率又迅速增大,因此标准差并不能作为失效率唯一的评判依据。
反舰导弹的贮存可靠寿命可根据其贮存失效率求得[10-11],如式(12)所示:
(12)
式中:L为反舰导弹贮存可靠寿命;λ为反舰导弹贮存失效率;R为临界可靠度的要求值。
通过式(12),可以根据不同要求值的临界可靠度,计算反舰导弹的贮存可靠寿命。例如:对于贮存失效率λ=0.134 976 3×10-6/h,满足可靠度R=99%,反舰导弹贮存寿命为:
3 结 论