基于极限学习机的风电机组叶根载荷辨识建模

秦 斌， 易怀洋， 王 欣

(湖南工业大学 电气与信息工程学院，湖南 株洲 412007)

风电机组单机容量不断增大，风机尺寸 增加，零部件柔度变大，由于风的随机性以及风剪切、塔影效应和湍流的影响，使得作用于风轮叶片和塔架等部件上的载荷存在不平衡性，引起机组零部件剧烈振动，导致零部件的疲劳损伤[1-2]。叶根部位载荷种类多、最复杂、影响大而且最易受到疲劳损伤，是风轮载荷比较集中的地方，进行叶根载荷主动控制研究极其重要。由于叶根载荷复杂、强耦合、不确定影响因素多，风的随机性以及风速、桨距角等主要影响因素与载荷的非线性关系，使得用传统基于内部机理分析为基础的机理建模方法很难建立叶根载荷的精确模型，且运算量大难以满足控制实时性要求[3]，文献[4]采用自由涡尾迹方法提高风力机气动载荷计算精度，构建了叶片的非线性动力学模型，但该方法比较复杂，计算量大。神经网络对非线性映射有任意逼近能力，为复杂非线性系统建模提供了理论基础。文献[5]基于现场数据利用BP算法建立了风电机组的BP神经网络动态模型；文献[6]利用SVM 建立了飞机机翼的载荷模型；文献[7]用极限学习机算法(ELM)建立了风功率密度预测模型。相比于传统的学习算法，ELM算法随机初始化输入权重和隐层偏置，不需要反复调节网络参数，泛化性能好，收敛速度快[8]。该研究将ELM算法首次引用到叶根载荷建模，建立ELM叶根载荷预测模型，并与利用SVM建立的叶根载荷模型进行比较，并与实际数据对比，验证了用ELM建立叶根载荷预测模型的可行性和精确性。

1 叶根载荷主要影响因素分析

风电机组承受的载荷主要有空气动力载荷、重力载荷、惯性载荷以及由变桨距、偏航控制等引起的载荷[9]。叶根载荷基于叶根坐标系，主要包括挥舞方向剪力和弯矩、摆振方向的剪力和弯矩以及俯仰力矩。为了分析叶根载荷的影响因素，可根据传统的数理方法进行分析。

图1为叶片受力示意图，空气动力载荷是叶片承受的主要载荷，假设叶素距叶根距离为r，根据叶素动量理论，叶片挥舞方向的剪力和摆振方向的剪力可以表示为：

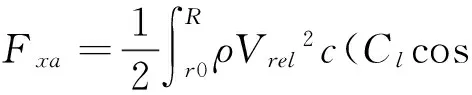
(1)

(2)

式中：Vrel为叶素处合成风速；ν为风速大小；ω为风轮旋转角速度；a为轴向诱导因子；b为周向诱导因子；ρ是空气密度；r0为轮毂半径；R为风轮半径；c是叶素的剖面弦长；Cl是升力系数；Cd是阻力系数；φ=α+β为入流角；α为攻角；β为桨距角。

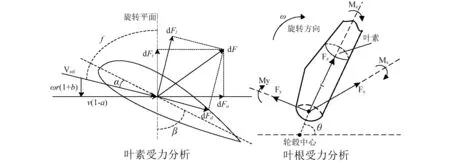
图1 叶片受力分析示意图Fig.1 Diagram of blade force analysis

风轮叶片根部的摆振力矩和挥舞力矩可以表示为[10]：

(3)

(4)

重力载荷主要使风轮叶片在摆振方向产生弯矩。方位角θ对摆振弯矩的大小有重要影响，详细可参考文献[11]。

风轮叶片除受到上述空气动力载荷、重力载荷外还有风轮旋转产生的离心力载荷，当风轮旋转并同时作偏航运动时，叶片上会产生垂直于风轮旋转平面的科氏力载荷，另外由于风机所处环境复杂，风速随机波动，以及风剪切、塔影效应和湍流的影响，风轮叶片所受载荷非常复杂，叶根部位的载荷就是这些载荷综合作用和耦合的结果，很难建立叶根载荷的精确模型。从上述基于叶素动量理论的叶片载荷分析中，可知叶根部位的载荷大小与风轮的规格尺寸和各项参数、风速、入流角、桨距角、方位角、风轮转速等因素有关，影响因素很多且相互耦合。该研究基于NREL 陆基5 WM风机数据，风机的轮毂高度90 m，风轮半径63 m，首先选取风速大小、桨距角、方位角、风轮转速、风速矢量与惯性坐标系3个轴的夹角等7个变量，取上述7个变量的数据，组成矩阵X(X1,X2,…X7)，对X进行主元分析，计算各主元的贡献率，矩阵X的协方差矩阵的前k个特征值的和除以它的所有特征值的和被称为X的前k个主元的累计贡献率，它表示了前k个主元包含的数据信息占全部数据信息的比例。前3个主元t1,t2,t3的贡献率分别为57.6%、23.9%和9.2%，累积贡献率达到90%以上，将原始数据7个变量降维为3个主元，然后通过计算HotellingT2统计量，T2统计量表示测量值在变动趋势和变化幅值上对模型的偏离度，计算出各变量对T2统计量的贡献大小[12]，根据贡献大小可确定叶根载荷的4个主要影响因素：风速ν、桨距角β、方位角θ和风轮转速ω，下文的叶根载荷ELM神经网络建模将以此为输入变量。

2 极限学习机算法

极限学习机(ELM)是由南洋理工大学黄广斌教授提出来的求解单隐层神经网络的算法。相比于传统的单隐层神经网络算法，ELM在保证学习精度较高的前提下，学习速度大大提高。

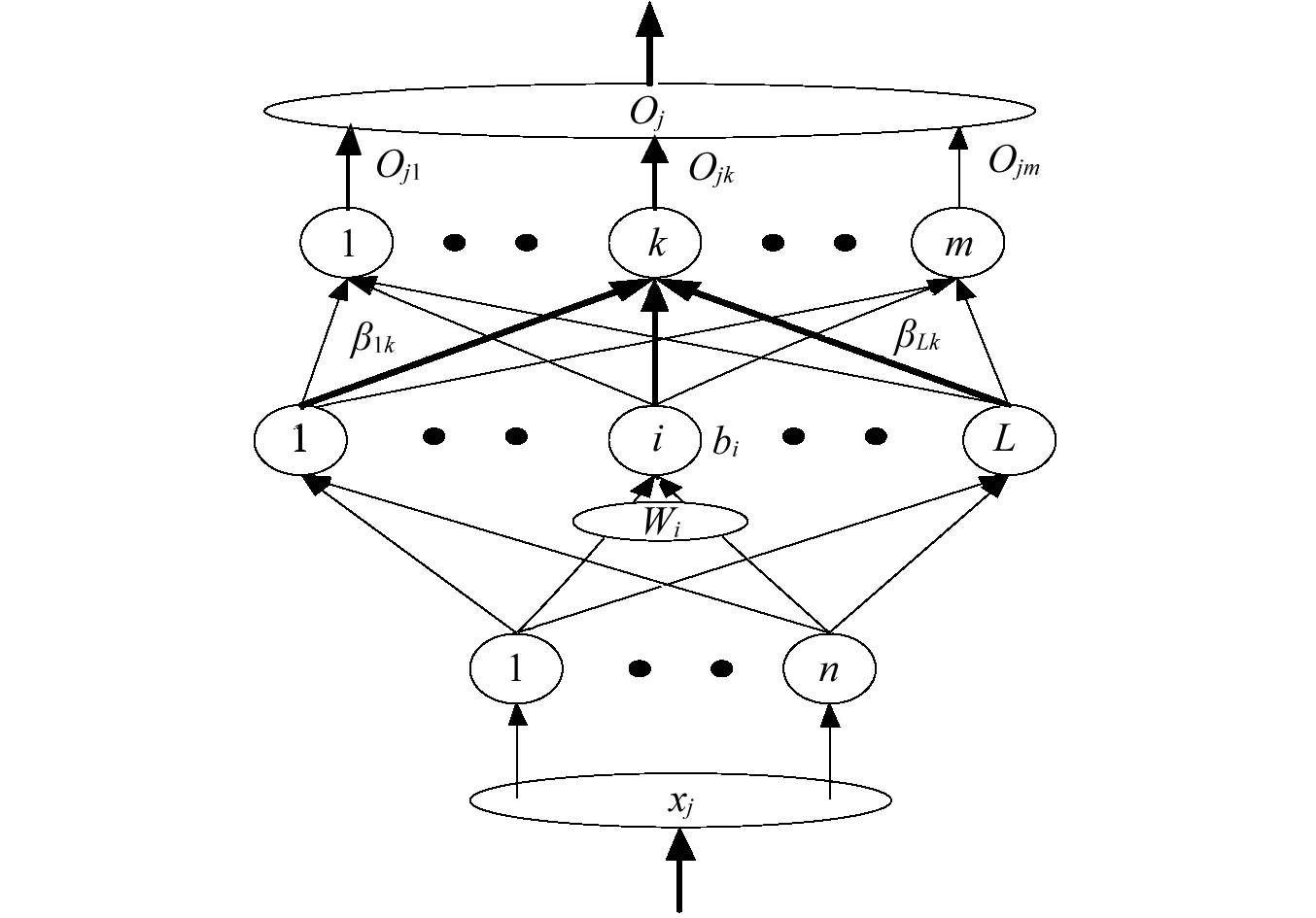
图2 单隐层前馈神经网络结构图Fig.2 Structure of single hidden layer feedforward neural network

设有N个不同的样本(Xi,ti)∈Rn×Rm，其中Xi=[xi1,xi2…xin]T，ti=[ti1,ti2,…tim]T对于如图2所示有L个隐层节点的单隐层前馈神经网络可以表示为：

(5)

(6)

式(6)的N个等式可用矩阵表示：

Hβ=T

(7)

式中：H为隐层节点的输出矩阵；β为输出权重矩阵；T为期望输出矩阵。

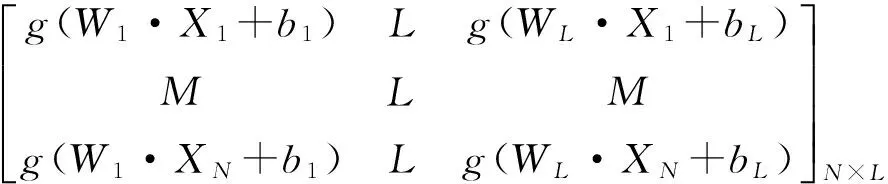
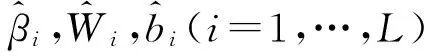
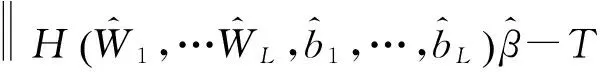
(8)

这等价于最小化损失函数：

(9)

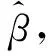
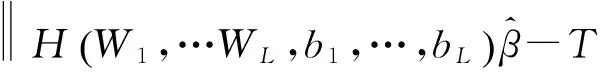
(10)

3 基于ELM的叶根载荷建模

变桨距风电机组根据风速情况和风力机功率特性的不同，可分为低于额定风速和高于额定风速两种工况，不同工况风速大小、功率和载荷情况有较大差别，该研究主要针对高于额定风速恒功率阶段，建立叶根载荷的ELM神经网络模型。运用雨流计数法对叶根部位疲劳载荷计算分析，发现叶根摆振方向弯矩Mx和挥舞方向弯矩My对叶根的影响较大，叶根部位俯仰弯矩Mz对叶根的影响较小[15-16]。综合考虑各种载荷对叶根部位的影响和建模的繁简，确定以摆振方向弯矩Mx和挥舞方向弯矩My为研究对象，以NREL 5 MW风电机组数据为基础，选取部分数据经过处理后作为ELM辨识建模的训练数据和测试数据，最后将测试数据与实际数据对比分析，验证ELM叶根载荷模型的精确性。建模步骤如图3。

图3 建模流程图Fig.3 The flow diagram of modeling

3.1 数据选取

以美国可再生能源实验室(NREL)[https://nwtc.nrel.gov/]陆基5 MW风机在研究工况下运行的数据为基础，随机选取900组数据作为ELM模型的训练数据和测试数据，验证ELM用于叶根载荷预测模型建模的可行性和精确性。如上文所述，以摆振方向弯矩Mx和挥舞方向弯矩My为研究对象，即以{Mx,My}作为ELM载荷预测模型的输出变量。经过上文分析叶根载荷有关的影响因素，以风速ν、桨距角β、方位角θ和风轮转速ω为模型的输入变量，即训练样本集为{ν,β,θ,ω;Mx,My}。在NREL 5 MW风机运行数据中，随机选取900组数据，其中720组数据作为训练集，剩下180组数据作为测试集。

3.2 数据预处理

为了消除量纲和单位不同对网络学习的影响，保证网络神经元的非线性作用及较快的学习速度，避免因净输入绝对值过大造成神经元的输出饱和，应将神经网络的样本数据进行归一化处理。按照归一化公式(11)将样本数据归一化到[0,1]区间。

(11)

3.3 确定网络结构

选用的网络结构为单隐层3层网络结构，激活函数采用Sigmoid函数，网络输入输出节点个数由网络输入输出变量而定，要建立的ELM神经网络叶根载荷预测模型有ν,β,θ,ω共4个输入变量以及Mx,My共2个输出变量，即所建ELM神经网络模型的输入节点个数确定为n=4，输出节点个数为m=2；在ELM算法中随机初始化输入权重Wi和隐层节点偏置bi，不需要迭代调整，只需要设置隐层节点个数，隐层节点个数的确定目前尚无理论指导。隐层节点数在一定范围内选取，ELM模型能保持稳定的泛化性能，但隐层节点过多或过少会使模型的泛化性能降低[8]。该研究用训练集和测试集进行测试验证的方法，以寻求测试误差最小来确定最优的节点数。图4表示隐层节点数目对ELM叶根载荷预测模型性能的影响，RMSE表示均方根误差，可以看出当隐层节点数较少时，ELM模型的训练误差和测试误差均随着隐层节点数的增加而急剧减小，当隐层节点数达到50左右，继续增加隐层节点数，训练误差和测试误差变化不显著，当节点数达到220点左右后，继续增加隐层节点数，测试误差反而增大且不稳定。在区间[100,220]范围内选取隐层节点数均能使ELM模型获得较好的预测精度，该研究隐层节点数选取为L=150。

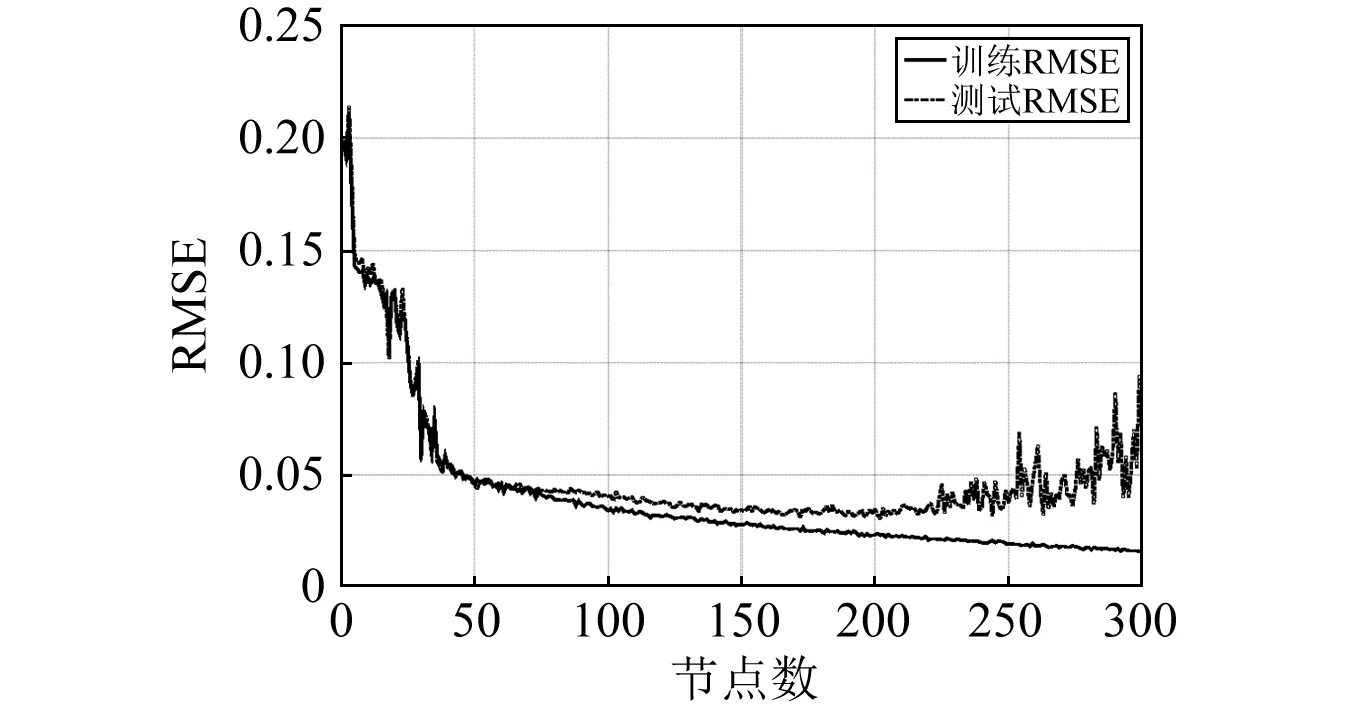
图4 隐层节点个数对ELM模型性能的影响Fig.4 The influence of the number of hidden nodes on the performance of ELM model

4 测试结果分析

ELM神经网络模型对复杂的非线性系统有较强的拟合能力，能根据给定的输入数据和输出的目标数据，寻找到输入数据和输出目标数据之间的映射关系。本研究用ELM算法对风电机组叶根载荷进行神经网络建模，是以ν,β,θ,ω4个输入变量和Mx,My2个输出变量的数据建立样本集，构建输入到输出的映射网络结构，对网络进行训练，神经网络就能找到输入和输出之间包含的映射关系，从而在相同的工况条件下任意给定输入也能给出较准确的预测输出，使网络具备泛化能力。建模过程如图3所示，ELM网络结构确定后，用5 MW风机的运行数据经过归一化处理后，建立输入和输出样本集对网络进行训练，目的在于找出蕴含在样本数据中的输入和输出之间的关系，当学习精度达到要求，网络隐层节点数固定下来，网络的输出权重向量也随之确定，这样ELM神经网络模型就已构建完成，任意给出同工况条件下的输入，就能根据公式(7)给出合适的输出。

为了比较ELM叶根载荷预测模型的性能，建立了叶根载荷SVM模型，并将ELM模型和SVM模型进行了对比研究。SVM叶根载荷建模基于台湾林智仁(Chih-Jen Lin)教授开发的支持向量机工具包LIBSVM，由于运用LIBSVM做回归预测时，只能对单输出变量建模，也就是一次只能对一个输出变量做拟合回归建模，所以分别建立摆振方向弯矩Mx和挥舞方向弯矩My的SVM模型。叶根载荷SVM模型的核函数采用径向基函数g(x)=exp(-γ*‖μ-ν‖2)，核函数参数γ和惩罚系数C是SVM建模的两个重要参数，两个参数对模型的预测精度和泛化性能影响很大，其中C用于调节置信范围和经验风险的比重，是调整模型复杂性和经验风险的参数。摆振方向弯矩Mx和挥舞方向弯矩My的SVM模型的核函数参数γ和惩罚系数C用网格搜索法寻优，以寻求一组合适的参数，使SVM模型拥有较小的训练误差和良好的泛化能力。通过参数寻优，叶根摆振方向弯矩SVM模型参数选取为γ=27.86，C=1.74；挥舞方向弯矩SVM模型参数选取为γ=84.45,C=1。图5和图6分别是摆振方向弯矩Mx和挥舞方向弯矩My的SVM模型的核函数参数γ和惩罚系数C用网格搜索法寻优的3D视图，其中纵坐标表示对应不同参数γ和C时SVM模型的训练误差，以均方误差MSE表示。

图5 Mx的SVM模型参数对训练误差的影响Fig.5 The influence of SVM model parameters on training error of Mx

图6 My的SVM模型参数对训练误差的影响Fig.6 The influence of SVM model parameters on training error of My

为了比较ELM载荷模型和SVM载荷模型的性能，分别对ELM模型和SVM模型进行了20次网络训练和测试，表1是一些指标的平均值。

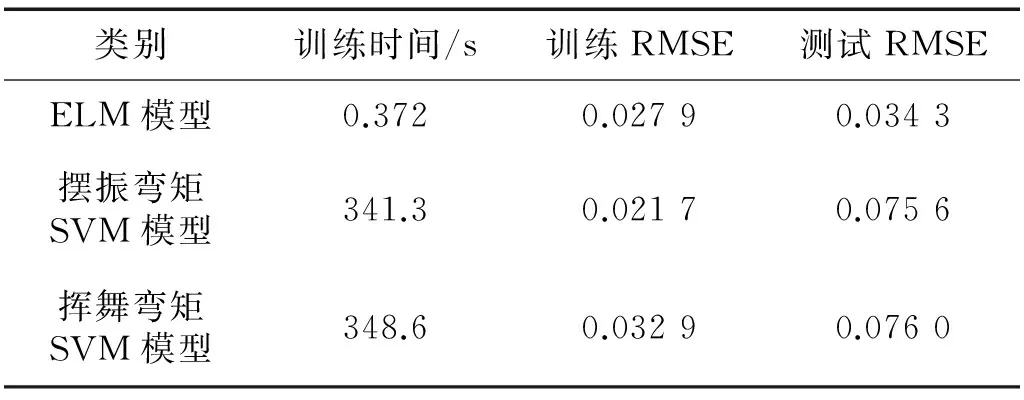
表1 ELM模型和SVM模型性能比较

用于网络训练和测试的电脑处理器是Intel Core i3-3240 3.4GHZ CPU，用MATLAB R2014b软件进行。因为ELM算法隐层节点个数对预测结果的影响并不灵敏，具有相同复杂度和样本个数的数据所需设置的隐层节点个数基本相同，可以通过选取900组数据进行训练来提前确定隐层节点的个数[17]，所以ELM训练时间没有计及确定隐层节点所需的时间；另外由于样本数较少，各模型的测试时间均较小且差别不大，故没有列出。由表1可以看出，ELM算法建立叶根载荷预测模型时，用均方根误差(RMSE)表示的训练误差与用SVM算法建立叶根载荷模型时的训练误差比较接近，但测试误差却小于SVM模型，预测精度比SVM高。而且运用ELM算法建模时，用于训练网络的时间要远远小于SVM建模时所需时间，表中数据显示ELM模型的训练速度是SVM的近千倍，即使计及隐层节点选取时间，ELM模型的训练速度也是SVM模型的数百倍，这是因为SVM模型训练过程中参数C和γ选取较麻烦费时。

图7～图10是用测试集的180组数据对ELM模型和SVM模型进行验证的仿真结果，分别运用ELM模型和SVM模型对叶根载荷进行预测后产生的载荷数据与实际数据进行对比。

图7 ELM模型预测的叶根摆振弯矩MxFig.7 Blade root edgewise moment Mx predicted by ELM model

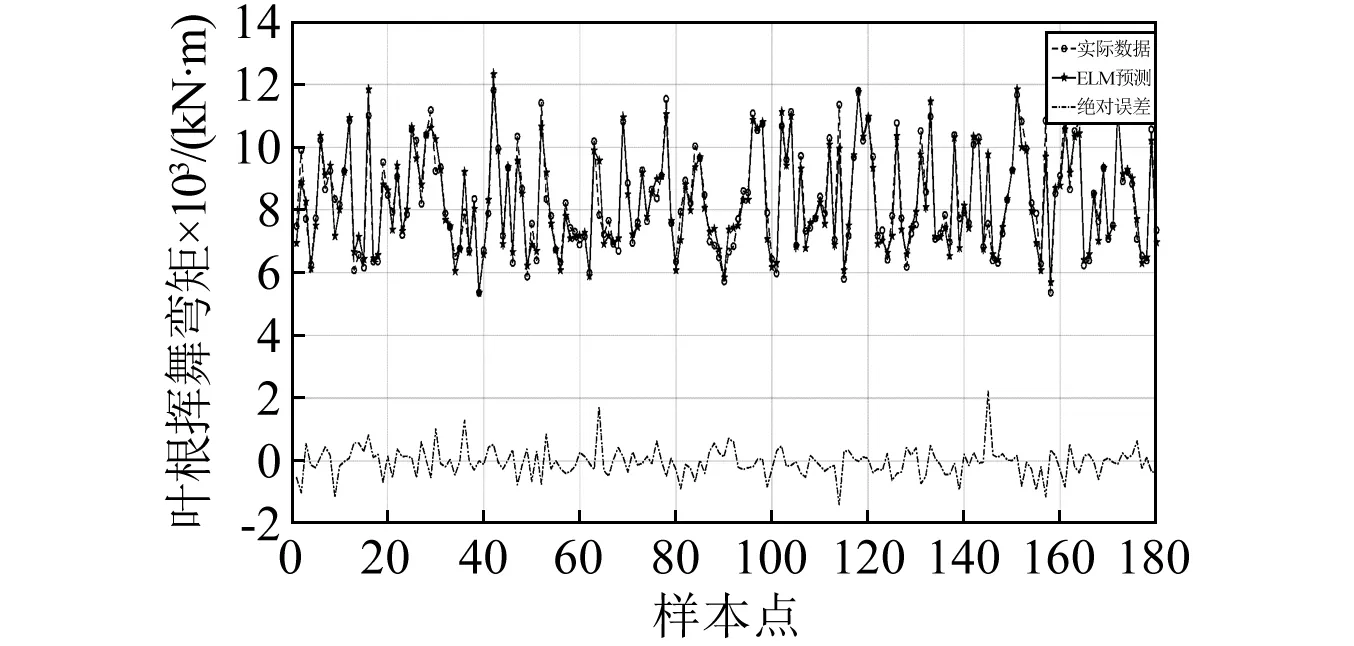
图8 ELM模型预测叶根挥舞弯矩MyFig.8 Blade root flapwise moment My predicted by ELM model

图9 SVM模型预测的叶根摆振弯矩MxFig.9 Blade root edgewise moment Mx predicted by SVM model

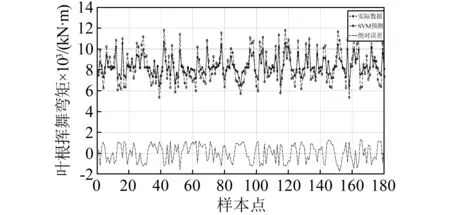
图10 SVM模型预测的叶根挥舞弯矩MyFig.10 Blade root flapwise moment My predicted by SVM model

图7是叶根摆振方向弯矩Mx的ELM模型预测数据和实际数据的对比图，可以看出ELM叶根载荷预测模型能够根据输入变量较准确地预测叶根载荷Mx的大小，预测可靠性较高，预测误差较小；图8是叶根挥舞弯矩My的ELM模型预测数据和实际数据的对比图，可以看出ELM叶根载荷预测模型根据风速、方位角等输入数据预测叶根挥舞弯矩My的准确率非常高；图9和图10分别是叶根摆振弯矩和挥舞弯矩的实际数据与SVM预测模型预测数据的对比图，可以看出SVM建立叶根载荷模型的预测精度不及ELM模型的预测精度，预测误差较大，而且预测误差的波动较大。从表1及图7～图10可以得出：在叶根载荷辨识建模上，ELM模型的精确度不仅高于SVM模型的精度，而且在叶根载荷建模网络训练的过程中，ELM模型的训练时间要远远小于SVM模型的训练时间，这种优良的性能将使ELM在复杂非线性系统辨识建模领域有更加广阔的应用前景。

5 结 论

针对叶根部位摆振弯矩和挥舞弯矩建立了ELM叶根载荷预测模型，并与SVM建立的叶根载荷模型进行了对比分析，结果表明ELM算法用于风轮叶根载荷建模的精确性较高，模型训练速度快，建模简单，从而说明ELM算法用于建立叶根载荷神经网络模型的可行性和精确性。现在大型风电场都有数据采集系统，这些采集的大量数据是一笔宝贵的资源，这些数据中蕴含着风电机组各方面的信息，而神经网络模型正可以利用这些数据辨识机组各方面的状态和性能，运用ELM算法进行风电机组建模不仅简单，而且预测精度高，可对机组性能和状态进行快速识别，为风机载荷建模和在线控制研究提供了一种行之有效的方法。叶根部位是风机载荷承载的关键部位，建立叶根载荷精确的预测模型对风电机组减振控制、控制性能优化有重要的作用。

[ 1 ] JOHNSONS J,BAKER J P, VAN D C P, et al. An overview of active load control techniques for wind turbine with an emphasis on microtabs[J]. Wind Energy, 2010, 13(2/3):239-253

[ 2 ] 肖帅, 杨耕, 耿华. 抑制载荷的大型风电机组滑模变桨距控制[J]. 电工技术学报, 2013, 28(7):145-150.

XIAO Shuai, YANG Geng, GENG Hua. Sliding-mode pitch control strategy for large wind turbines to reduce loads[J]. Transactions of China Electrotechnical Society, 2013, 28(7):145-150.

[ 3 ] YAO X, WANG X, XING Z, et al. Individual pitch control for variable speed turbine blade load mitigation[C]// IEEE International Conference on Sustainable Energy Technologies. IEEE, 2008:769-772.

[ 4 ] 曹九发, 王同光, 王枭. 大型风力机的几何非线性动态响应研究[J]. 振动与冲击, 2016, 35(14):182-187.

CAO Jiufa, WANG Tongguang, WANG Xiao. Geometric nonlinear dynamics response of large-scale wind turbine[J]. Journal of Vibration and Shock, 2016, 35(14):182-187.

[ 5 ] 王爽心, 李朝霞. 变桨距风电机组自适应PI优化控制[J]. 太阳能学报, 2013, 34(9):1579-1586.

WANG Shuangxin, LI Zhaoxia. Adaptive PI optimization control for variable-pitch wind turbines[J]. Acta Energiae Solaris Sinica,2013, 34(9):1579-1586.

[ 6 ] 郝云霄, 闫楚良, 刘克格. 基于支持向量机的机翼载荷模型研究[J]. 科学技术与工程, 2013, 13(25):7432-7437.

HAO Yunxiao, YAN Chuliang, LIU Kege. Modeling aircraft wing loads based on support vector machine[J]. Science Technology & Engineering, 2013,13(25):7432-7437.

[ 7 ] MOHAMMADI K, SHAMSHIRBAND S, YEE P L, et al. Predicting the wind power density based upon extreme learning machine[J]. Energy, 2015, 16:232-239.

[ 8 ] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/2/3):489-501.

[ 9 ] 刘军, 陈东亮. 基于神经网络风力发电机组载荷优化控制策略研究[J]. 电气传动, 2014, 44(2):59-63.

LIU Jun, CHEN Dongliang. Optimal control strategy for wind turbine load reduction based on neural network[J]. Electric Drive, 2014,44(2):59-63.

[10] 刘皓明, 唐俏俏, 张占奎,等. 基于方位角和载荷联合反馈的独立变桨距控制策略研究[J]. 中国电机工程学报, 2016, 36(14):3798-3805.

LIU Haoming, TANG Qiaoqiao, ZHANG Zhankui, et al. Study of individual pitch control based on azimuth angle and load feedback[J]. Proceedings of The Chinese Society for Electrical Engineering, 2016, 36(14):3798-3805.

[11] 何伟. 湍流风场模拟与风力发电机组载荷特性研究[D]. 保定：华北电力大学, 2013.

[12] 张小桃, 倪维斗, 李政,等. 基于主元分析与现场数据的过热汽温动态建模研究[J]. 中国电机工程学报, 2005, 25(5):131-135.

ZHANG Xiaotao, NI Weidou, LI Zheng, et al. Dynamic modeling study of superheater steam temperature based on principal component analysis method and online data[J]. Proceedings of the Csee, 2005, 25(5):131-135.

[13] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: a new learning scheme of feedforward neural networks[J]. Proc.int.joint Conf.neural Netw, 2004(2):985-990.

[14] BARTLETT P L. For valid generalization, the size of the weights is more important than the size of the network[J]. Advances in Neural Information Processing Systems, 1997:134-140.

[15] 陈严, 张林伟, 刘雄,等. 水平轴风力机叶片疲劳载荷的计算分析[J]. 太阳能学报, 2013, 34(5):902-908.

CHEN Yan, ZHANG Linwei, LIU Xiong, et al. Fatigue load calculation and analysis of the blade of horizontal axis wind turbine[J]. Ata Energiae Solaris Sinica, 2013, 34(5):902-908.

[16] DING C Y, LI G Q, GUO H C. Fatigue analysis of wind turbine[J]. Applied Mechanics & Materials, 2012, 229/230/231:621-624.

[17] 张颖, 李梅, 高倩倩,等. 基于 ELMR-SVMR 的海水水质预警模型研究[J]. 大连理工大学学报, 2016, 56(2):185-192.

ZHANG Ying, LI Mei, GAO Qianqian, et al. Research on forewarning model of seawater quality based on ELMR-SVMR[J]. Journal of Dalian University of Technology, 2016,56(2):185-192.