轴系运行工况对轴系-基座-壳体耦合振动影响研究

蔡耀全， 曾凡明， 刘金林， 刘树勇

(海军工程大学 动力工程学院，武汉 430033)

目前关于螺旋桨不均匀伴流场作用在船体艉部结构上引起的振动研究较多，而对于螺旋桨推进轴系与船体艉部的耦合振动研究较少。从国内外公开的资料来看， 针对油船、集装箱船和散货船，开展了大型船舶在船舶平浮、压载和满载工况下船体变形计算研究；研究了齿轮任意布置时轴承的受力情况以及受力方向，并研究对轴系校中的影响；开展了船体变形对轴系校中的影响研究；开展了环境安装温度对轴系校中的影响研究[1]。挪威船级社(Det Norske Veritas, DNV)考虑船体—推进耦合的轴系校中精确解析计算项目；英国劳氏船级社则开发了(Evaluation of Revers Alignment, ERA) 软件系统来评估轴承对轴系校中的影响[2]。

Larsen[3]于1976 年就指出在轴系校中过程中需要考虑吃水变化、热效应、螺旋桨推力波动、止推轴承推力座倾斜以及轴承柔性等因素的影响。朱军超[4]以船舶推进轴系为研究对象,从尾轴承有效接触长度、轴承支撑刚度、船体变形引起轴承位置的变化这三个方面来研究轴承支撑状态对轴系振动的影响。石磊[5]基于轴系合理校中有限元法基本原理，对某船轴系进行校中，分析表明轴承润滑状态、船体变形、船舶装载、波浪载荷和环境温度综合作用对轴系校中状态影响显著。对于轴系振动和艇体尾部激励研究主要集中在单独研究轴系回旋振动、扭转振动和纵向振动以及相互之间的耦合振动。李栋梁等[6]对推力轴承的动力学特性进行研究，计算了不同转速下推力轴承油膜刚度，并将其应用到轴系-艇体结构耦合系统中，分析了其影响。刘耀宗等[7]针对潜艇推进轴系纵向振动特点，建立其轴系计算模型，分析了安装纵向减振器对纵向减振的影响。孟浩[8]在研究潜艇轴系纵向振动传递问题的基础上，应用声子晶体局域共振带隙原理，在潜艇轴系上加装多个局域振子，利用遗传算法来优化振子力学参数，降低了轴系对螺旋桨脉动推力的传递。曹贻鹏[9]建立带有推进轴系的水下壳体结构计算模型，使用有限元/直接边界元方法对螺旋桨横向、纵向脉动激励引起的壳体结构辐射噪声规律特性进行分析，并提出了相应减振措施。李良伟等[10]基于达朗伯原理建立船舶轴系纵向振动数学模型，导出动力减振器响应位移的动力放大系数解析式，运用动力调谐消振理论求解最优固有频率比和最优阻尼比，为轴系纵向振动控制及动力减振器的设计提供理论了依据。

综上所述，对于轴系-基座-船体耦合振动研究主要从校中方面考虑，将船体的影响单独引入到轴系中进行振动计算，对于轴承的处理也过于简单，这样对于轴承负荷变化、轴承油膜刚度和阻尼变化对整个系统耦合振动影响并没有考虑。本文结合现有资料，建立轴系-基座-壳体有限元模型，计算不同工况时油膜刚度和阻尼特性，利用有限元功率方法流分析研究支撑轴承特性对轴系-基座-壳体耦合振动影响，为船体艉部减振降噪提供有效计算方法。

1 轴承刚度和阻尼矩阵求解

1.1 油膜刚度和阻尼刚度矩阵建立

试验台轴系组成：一个力加载轴、一个圆盘(模拟螺旋桨)、一个尾轴、一个中间轴和一个推力轴；尾轴由尾管后轴承、尾管前轴承两个轴承支撑，推力轴由一个推力轴承支撑；尾轴与中间轴通过半联轴节连接，中间轴与推力轴之间通过法兰连接；螺旋桨用圆盘模拟。根据推进轴系试验平台实际结构，将三个轴承分别作为连续弹性支承处理。本文主要研究支撑轴承和推力轴承推力块上油膜特性对轴系-基座-壳体影响，因此需要同时计算不同工况下轴承支撑油膜刚度和推力块刚度。对于后艉轴承、前艉轴承和电机支撑轴承采用如图1所示处理，离散后每个轴承油膜单元如图2所示。对于后艉轴承S=5，前艉轴承S=4，电机支撑轴承为S=2。

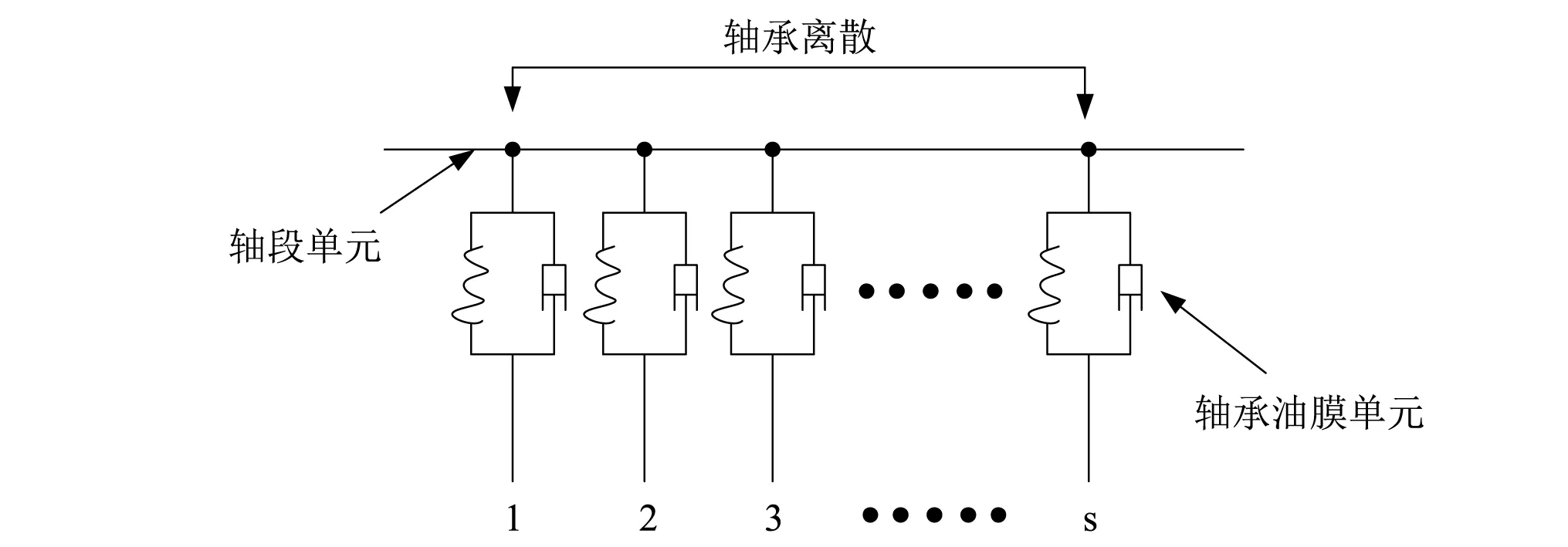
图1 支撑轴承连续弹性支承处理Fig.1 Aft stern bearing discrete

图2 轴承油膜单元Fig.2 Bearing oil film element

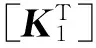
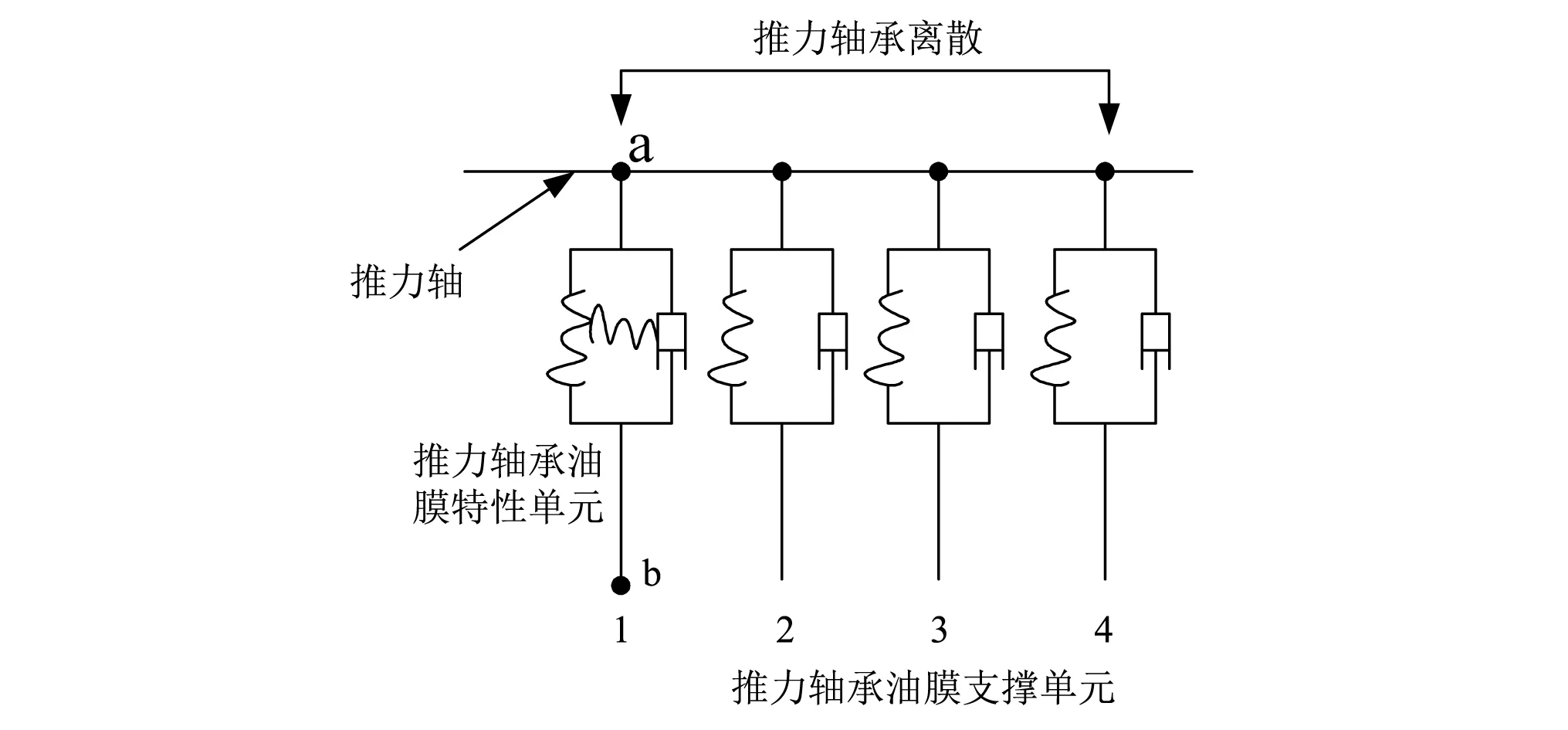
图3 推力轴承离散处理Fig.3 The discrete process of thrust bearing

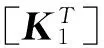
2 有限元功率流计算

2.1 系统有限元基本方程构建

基于Hamilton原理和有限元法建立轴系-基座-壳体系统动力学模型，由于系统中有处于转动的轴系，因而系统动力平衡方程构成有所不同，对于静止不动的壳体，其动力平衡方程如下：

(1)

式中：Fk为壳体外载荷矢量，Mk、Ck和Kk分别为壳体质量矩阵、壳体阻尼矩阵和壳体刚度矩阵。对于旋转的轴系，由于螺旋桨的重量导致轴系变形，在转动时产生的陀螺效应需要加以考虑，其动力平衡方程如下：

(2)

式中：Fs为轴系外载荷矢量，Ms、Cs和Ks分别为轴系质量矩阵、轴系阻尼矩阵和轴系刚度矩阵；Gs为陀螺矩阵，Bs也为旋转阻尼矩阵，两者参与计算时主要取决于轴系旋转速度，前者做主要贡献。

对于轴承采用本文离散的轴承油膜单元模拟，以轴承力的形式与转轴耦合：

(3)

对式(1)～(3)单元方程进行组装，即可得到轴系-基座-壳体系统运动方程：

(4)

式中：Msys、Csys和Ksys为系统质量矩阵、阻尼矩阵和刚度矩阵；Fsys系统外载荷矢量，在计算时涉及到的外载荷矢量包含有重力Fg、轴系上螺旋桨激振力Fp、刚性法兰不对中激振力Fgf和高弹不对中激振力Fgt以及电机驱动力矩Fd和激振力分量Fdf[11]。

2.2 有限元功率流计算基本方法

对于轴系-基座-壳体系统，主要是研究系统在稳态激励作用下轴系传递到壳体上的功率流特性。因此稳态激励下，功率流计算式如下：

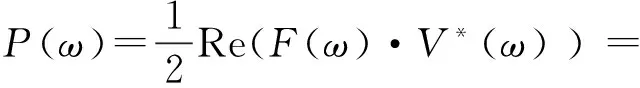
(5)

式中：Re和Im分别代表取复数实部和虚部；F(ω)、V*(ω)和U*(ω)分别为傅里叶变换后力的复数、速度复数和位移复数；*表示取共轭。

对于式(4)，分析中，可将位移表达为：

(6)

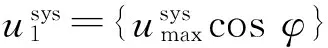
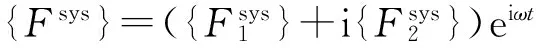
(7)

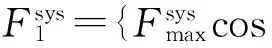
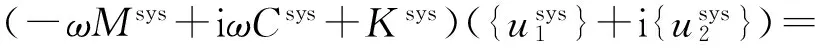
(8)

对式(8)进行求解，就可得到系统中各单元节点的力和位移的频率响应复数值，结合式(5)就可求得节点功率流。

计算各支撑轴承即传递路径流进的功率流。单个轴承油膜单元的功率流计算如下：

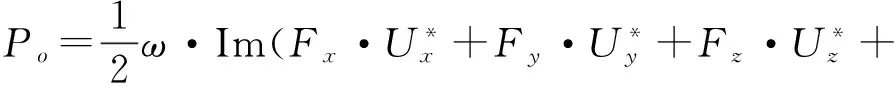
(9)

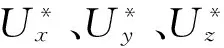
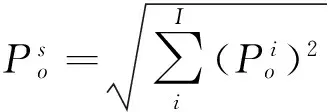
(10)

对于后艉轴承和电机支撑轴承分别为i=5和i=4。 对于前艉轴和推力轴承，由于采用实体建模，并且考虑到两者上还需安装动力吸振器等因素，因此不能从轴承支撑处来评价，需从两者与壳体连接处的功率流来进行评价，对于前艉轴承，其连接处如图(4)所示。对于这两处的功率流计算方法参考文献[12]。前艉轴承处共60个单元224个评价节点，推力轴承连接处为24个单元，共75个评价点。

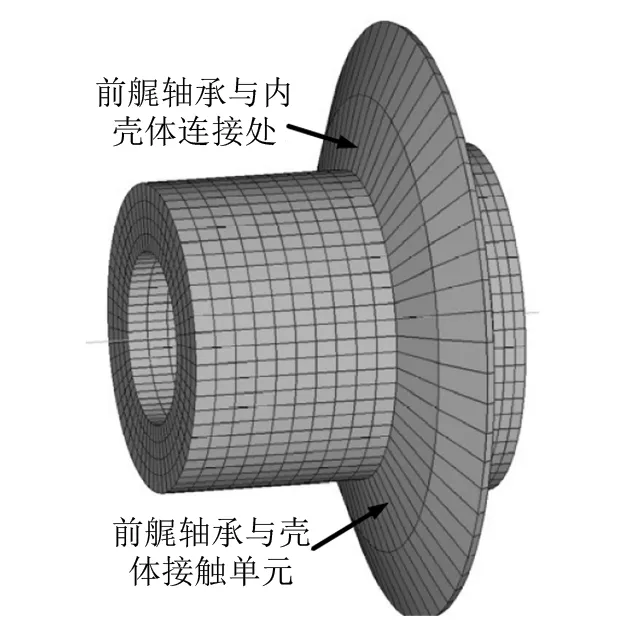
图4 前艉轴承连接处Fig.4 Former stern bearing connected

图5 推力轴承连接处Fig.5 Thrust bearing bearing connected

3 系统动力响应计算

3.1 系统仿真参数及其方程求解

以某推进轴系试验平台轴系为基础，建立轴系-基座-壳体系统模型如图6，分析不同工况下，轴承支撑特性对系统耦合振动影响规律。模型计算参数如下。

图6 系统模型Fig.6 The system model

螺旋桨、半联轴器，高弹联轴器及电机转子的极转动惯量分别为3 250 kg·m2、125 kg·m2、365 kg·m2和2 550 kg·m2；轴系密度、泊松比、弹性模量和切变模量分别为7 850 kg/m3、0.26、2.1E+011 Pa 和0.769E+011 Pa；高弹联轴器扭转刚度kn=2.6E+006 N·m/rad，径向刚度为7.8 E+006 N/m。计算工况：轴系转速为70 r/min、100 r/min、200 r/min和300 r/min；相对应于这四种工况，分别计算支撑轴承和推力块的油膜动力特性系数，代入系统模型进行计算；计算所施加外载荷按式(4)中计算。由于轴系不对中和螺旋桨重力造成轴系呈弯曲状态，因而轴系在旋转时会产生陀螺效应，为此本文计算时，先进行静态计算，再对轴系运转进行有预应力的频率响应分析，这样就可以将轴系变形时产生的弯曲应力和位移考虑到动态结果中，得到轴系在弯曲状态下运行的结果。

3.2 系统仿真结果

为详细分析轴系不同工况对轴系-基座-壳体的影响，分别计算四种工况下流经四个传递路径的功率流，以评价其影响，得到图7～图10。

由图7～图10可得如下结论：

(1)随着转速上升，各轴承油膜支撑刚度降低，流入各轴承的功率流发生改变。对于后艉轴轴承和前艉轴来说，影响较大，推力轴承和电机支撑轴承影响较小。主要原因是因为后艉轴承和前艉轴承是水润滑橡胶轴承，橡胶支撑刚度相对于推力轴承轴瓦支撑来说刚度很低，再加上由于转速上升使得油膜刚度降低，使得后艉轴承和前艉轴承处轴系对位移更加敏感，横向振动位移加大，轴系弯曲应力增加，而对于推力轴承和电机支撑轴承油膜刚度对其自身影响不太大，而功率流计算主要是依靠节点力和位移，因此转速变化对于后艉轴承和前艉轴的支撑特性影响较大，并且随转速增加，功率流特性有向左移趋势，这是由轴承润滑特性引起。

图7 流经后艉轴承功率流Fig.7 Aft bearing power flow at different operating condition

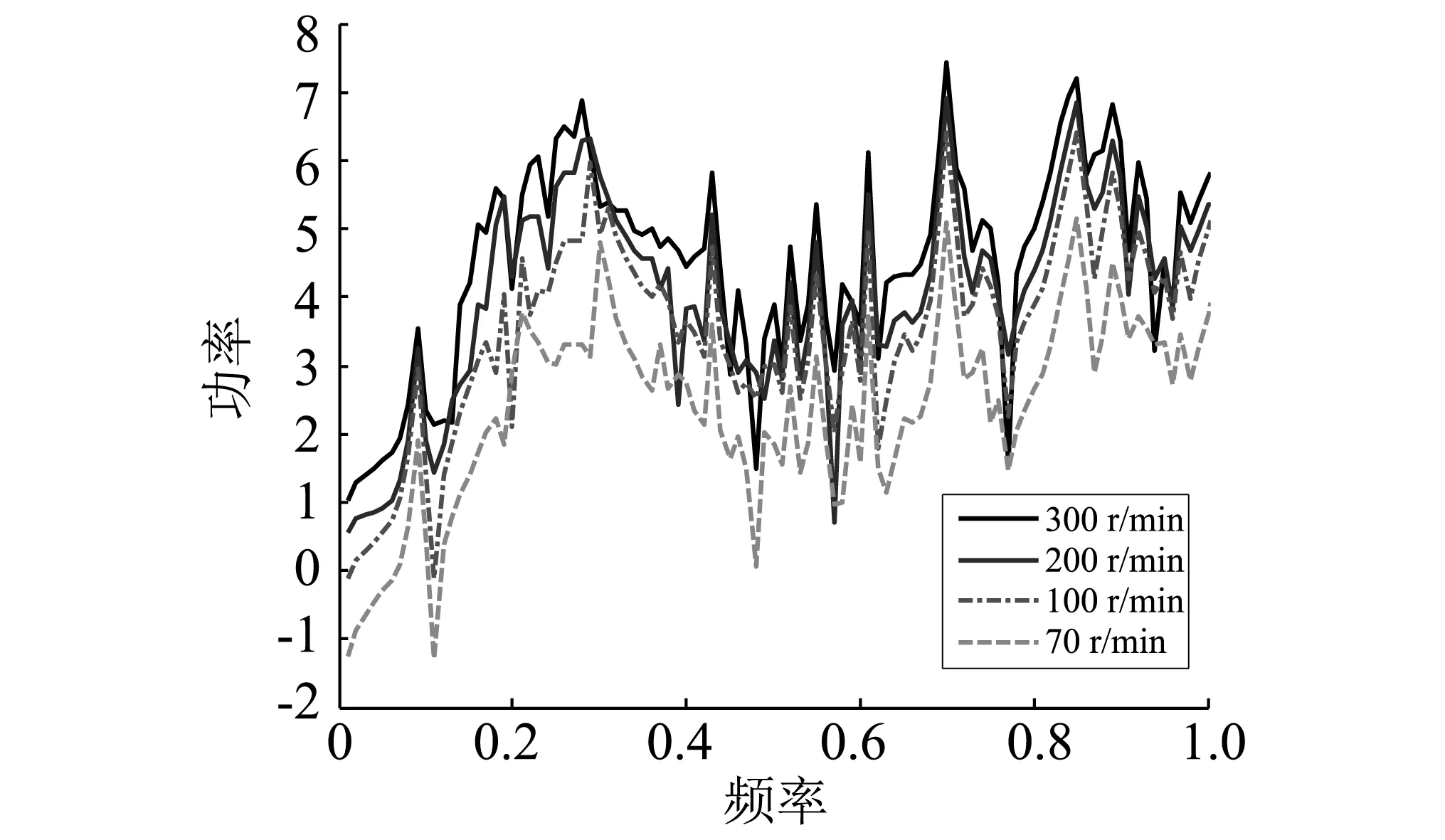
图8 流经前艉轴承功率流Fig.8 Former bearing power flow at different operating condition

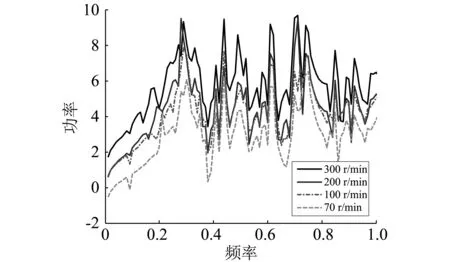
图9 流经推力轴承功率流Fig.9 Thrust bearing power flow at different operating condition

图10 流经电机轴承功率流Fig.10 Motor bearing power flow at different operating condition

(2)对于推力轴承来说，功率流特性左移不明显，主要原因有两点：一是对轴承润滑特性改变敏感度相对较低，另一个原因是因为随着轴系转速上升，推力轴承油膜刚度增加，推力轴承推力块油膜润滑特性是向右移动，由于纵向振动对回旋振动有影响，使得对其承支撑油膜润滑特性有向右移影响，这就使得图9上功率流曲线左移特性不明显，只是在大小上有些区别。

(3)从图7～10可以看出，流经推力轴承功率流最大，电机支撑轴承、后艉轴和前艉轴相对较小。流经轴承的功率流大小可间接反映对壳体二次激振引起的噪音大小。轴系的激振力通过推力轴承传递到壳体引起振动和噪音是主要途径。但也不能忽视后艉轴承、前艉轴承和电机支撑引起的振动和噪音，其值也并不小，主要原因是螺旋桨激振横向激振力及其弯矩、纵向和回旋耦合振动和螺旋桨重力与船体尾部共同耦合振动，使得船体尾部振动和噪音更加复杂。此外，轴系在不同工况运行时其幅频特性随转速上升而左移，这一现象与文献[13]中关于轴系-壳体耦合振动控制试验的结果相一致，验证了本文所采用功率流有限元方法对系统分析的正确性。

图11～图13为不同工况下，轴上某一参考点纵向振动和回旋振动响应。可知：

(1)轴系在Y和Z方向上出现左移特性，其原因由于轴承润滑特性所引起，在X方向上表现不明显。

(2)轴系在中低频处X，Y和Z方向都出现多个振动峰值，主要原因是因为轴系通过轴承与船体耦合产生。由于船体艉部结构复杂因而在低频处具有许多模态，这一点可通过船体模态分析可知，尤其是艉部模态频率较多。因此，在多激励下，轴系与船体耦合导致轴系在低频处出现许多振动峰值，由此可见船体艉部设计对于艉部耦合振动影响尤为重要。

(3)轴系Y向振动和Z向振动有较大不同，主要原因是应为两个方向上油膜动力特性参数不一样，本文通过计算支撑轴承油膜动态特性参数表明，Y向和Z向的油膜刚度和阻尼相差很大，前者是后者好几倍，并且两个方向还存在耦合系数的影响，再加上Y方向有重力影响，使得和壳体耦合加剧。因此Y向和Z向表现出不一样的振动特性。

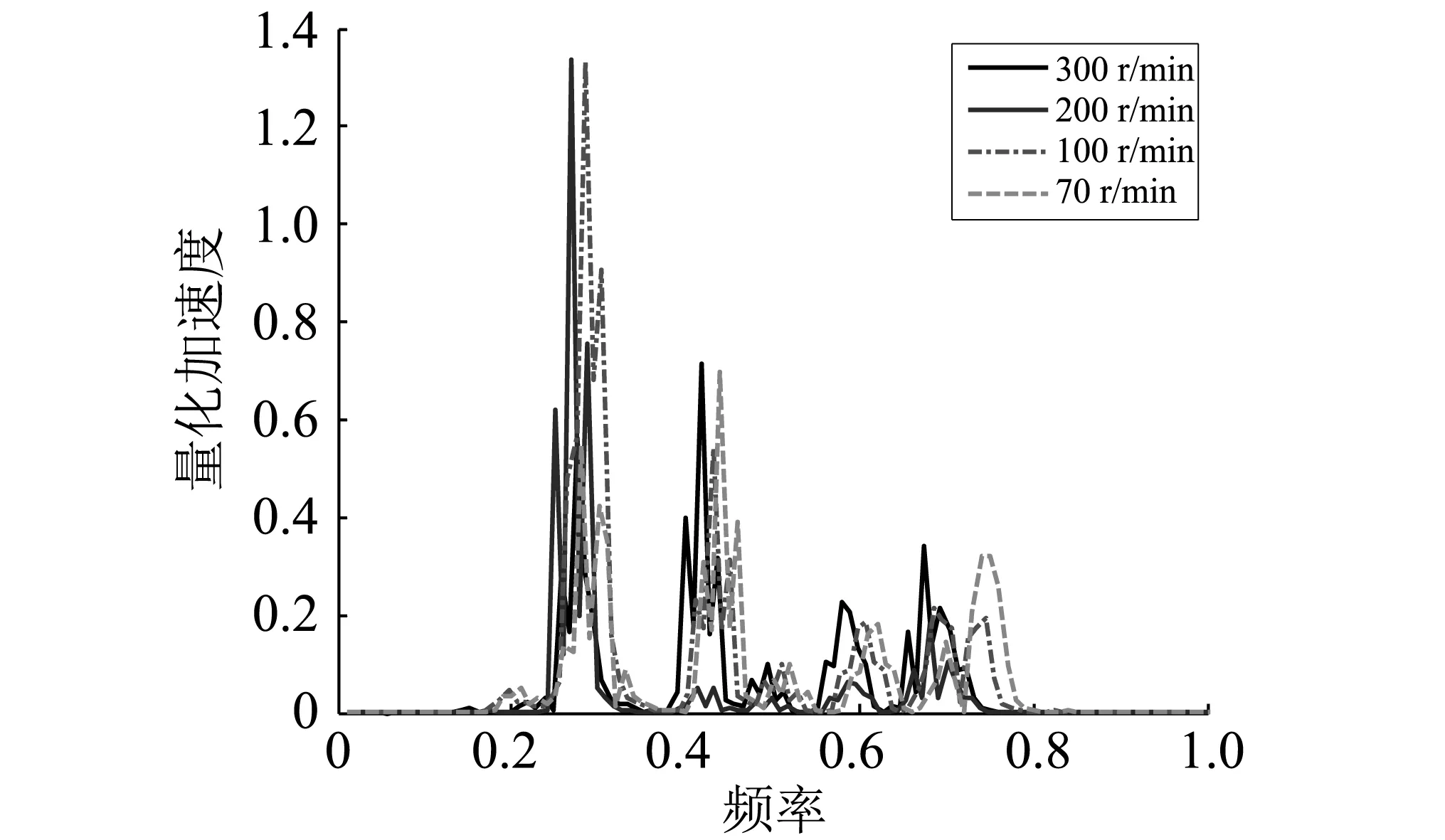
图11 参考点X向振动加速响应(不同工况)Fig.11 X vibration response of shafting reference point (different operating conditions)

图12 参考点Y向振动加速响应(不同工况)Fig.12 Y vibration response of shafting reference point(different operating conditions)

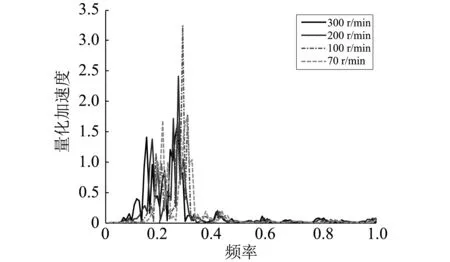
图13 参考点Z向振动加速响应(不同工况)Fig.13 Z vibration response of shafting reference point(different operating conditions)

图14～图16为同工况下不同参考点振动响应。可知，激振力在经过不同路径传递后会引起不同振动响应，各轴承传递特性不一样，在低频处，不同方向上均有丰富的振动峰值，这与壳体结构和支撑轴承特性有关。

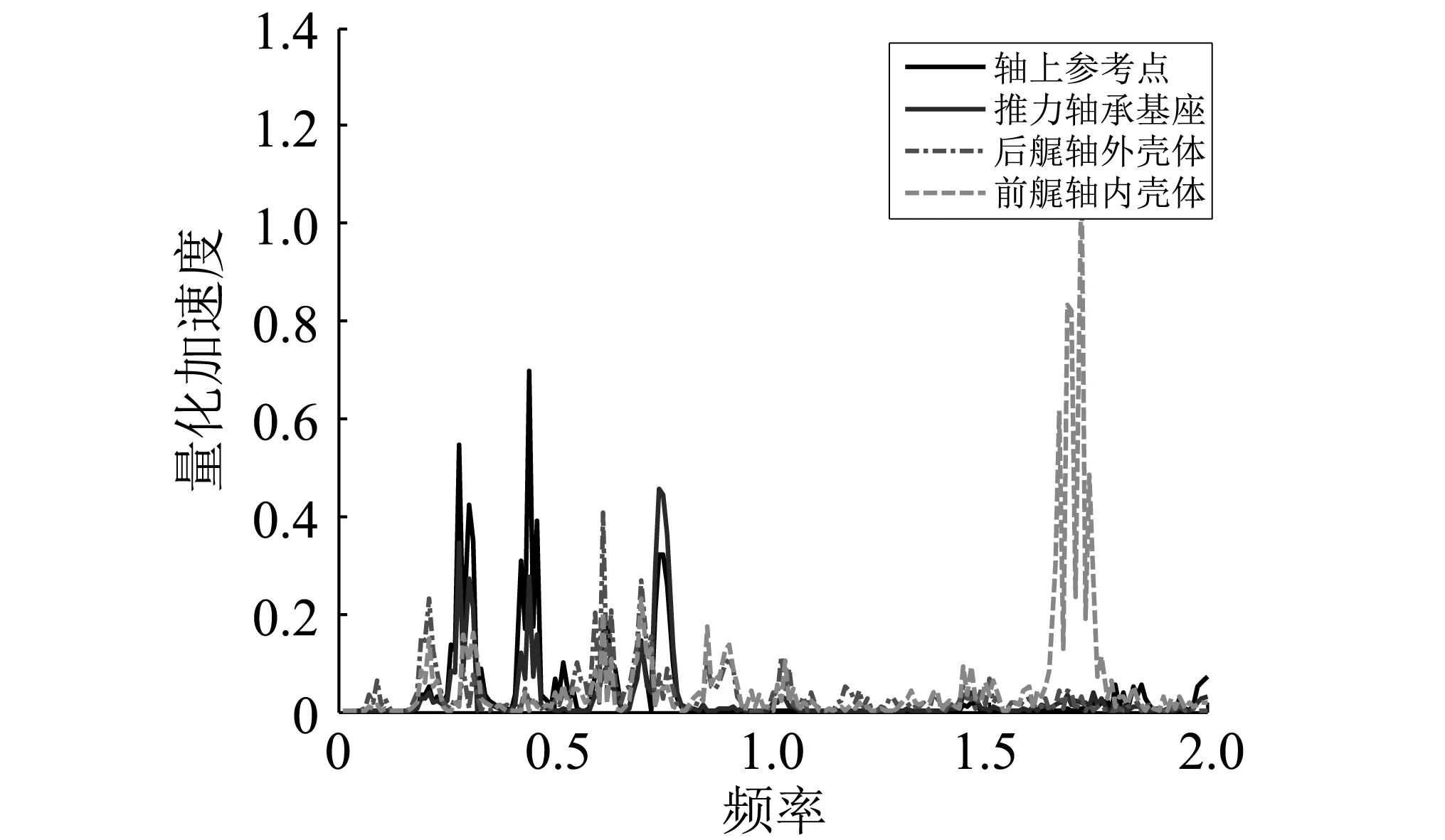
图14 参考点X向振动加速响应(同工况)Fig.14 X vibration response of shafting reference point(same operating conditions)

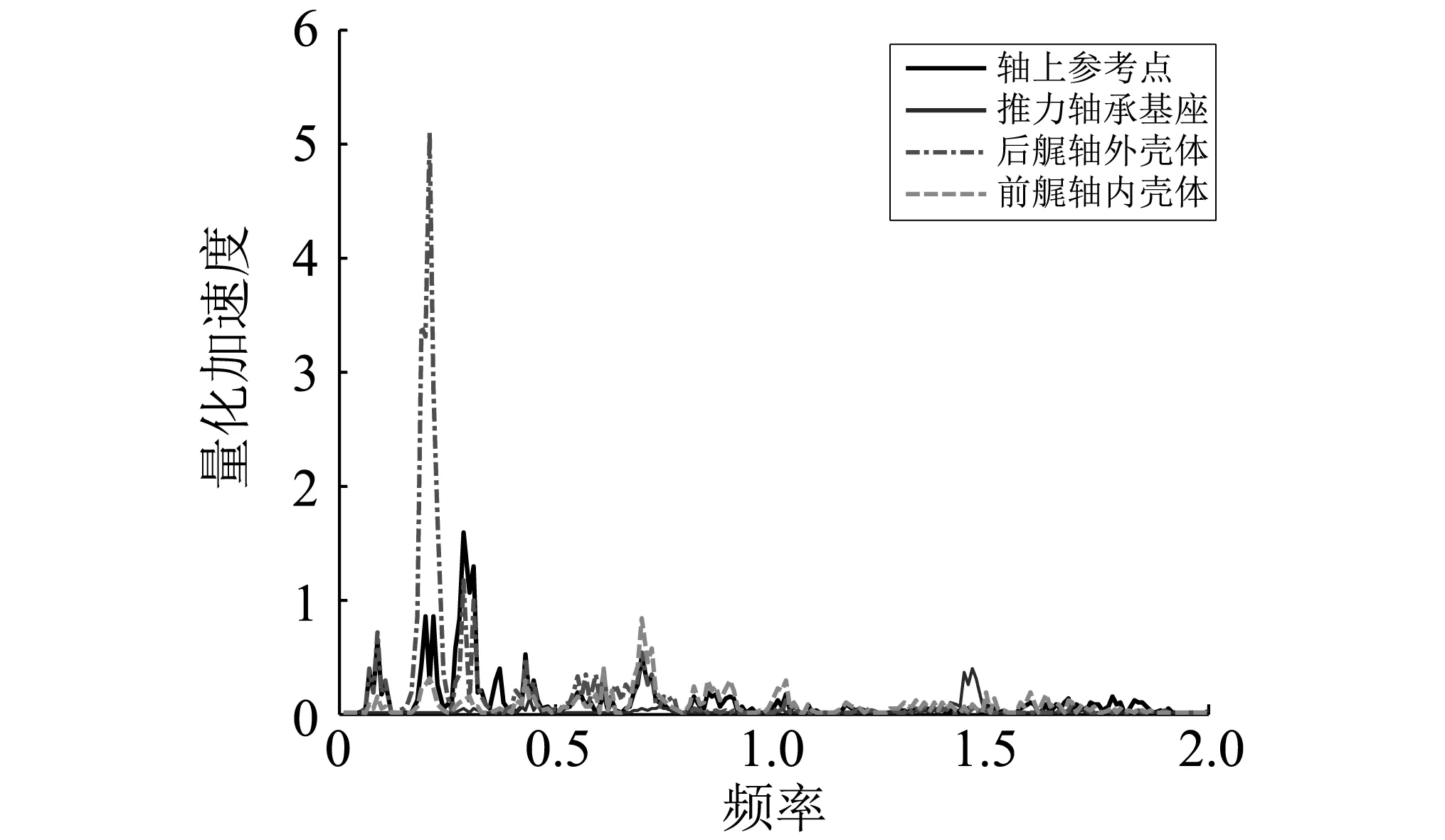
图15 参考点Y向振动加速响应(同工况)Fig.15 Y vibration response of shafting reference point(same operating conditions)

图16 参考点Z向振动加速响应(同工况)Fig.16 Z vibration response of shafting reference point(same operating conditions)

为清楚了解轴系在旋转时产生的陀螺效应，本文计算得到了轴系涡动轨迹图。取轴系转速300 r/min时，低频处对系统能量做主要贡献的频率0.14 Hz、0.26 Hz、0.33 Hz和0.39 Hz，得到轴系相应涡动轨迹图17～图20。

图中轴系量化长度在[19, 55]、[118, 137]、[215, 225]和[273, 283]处相对于轴系中后艉轴承、前艉轴承、推力轴承以及电机支撑轴承。由这些涡动轨迹图可看出，轴系在自身旋转下绕着中心轴旋转，发生偏离，产生陀螺效应。由于支撑轴承的各向异性，导致轴系上各点以椭圆轨道运行，其椭圆轨迹大小与系统振动频率有关。在图17中以螺旋桨作用点涡动轨迹最长，其次是后艉轴承至前艉轴承间艉轴离散点涡动轨迹较长，可称为系统“一阶”回旋耦合振动。在图18中仍以螺旋桨作用点涡动轨迹最长，其次涡动轨迹较长的为半联轴器和高弹联轴器作用点，可称为系统“二阶”回旋耦合振动。图19中仍以半联轴器作用点涡动轨迹最长，其次涡动轨迹较长的为螺旋桨和高弹联轴器作用点，可称为系统“三阶”回旋耦合振动。对于图20，可明显看出在后艉轴承和前艉轴承间艉轴段涡动轨迹最长，且远远超过其它任何离散点涡动轨迹，可称为系统“一阶”纵向耦合振动。由涡动轨迹图可看出，轴系-基座-壳体的耦合使得轴系呈现出新的共振频率和丰富的振型，在各频率段均表现出不同涡动轨迹。轴系的涡动轨迹对于船体艉部振动噪音的识别具有重要的参考价值。

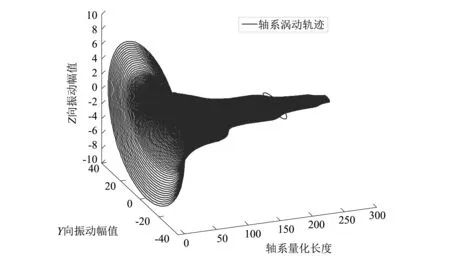
图17 0.14 Hz时轴系涡动轨迹图Fig.17 0.14 Hz shafting whirl orbit

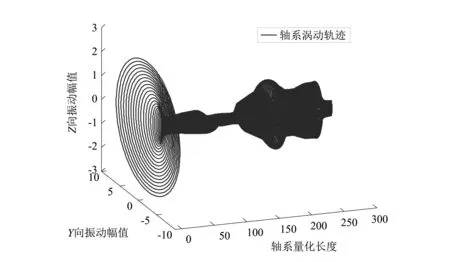
图 18 0.26 Hz时轴系涡动轨迹图 Fig.18 0.26 Hz shafting whirl orbit

图 19 0.33 Hz时轴系涡动轨迹图 Fig.19 0.33Hz shafting whirl orbit

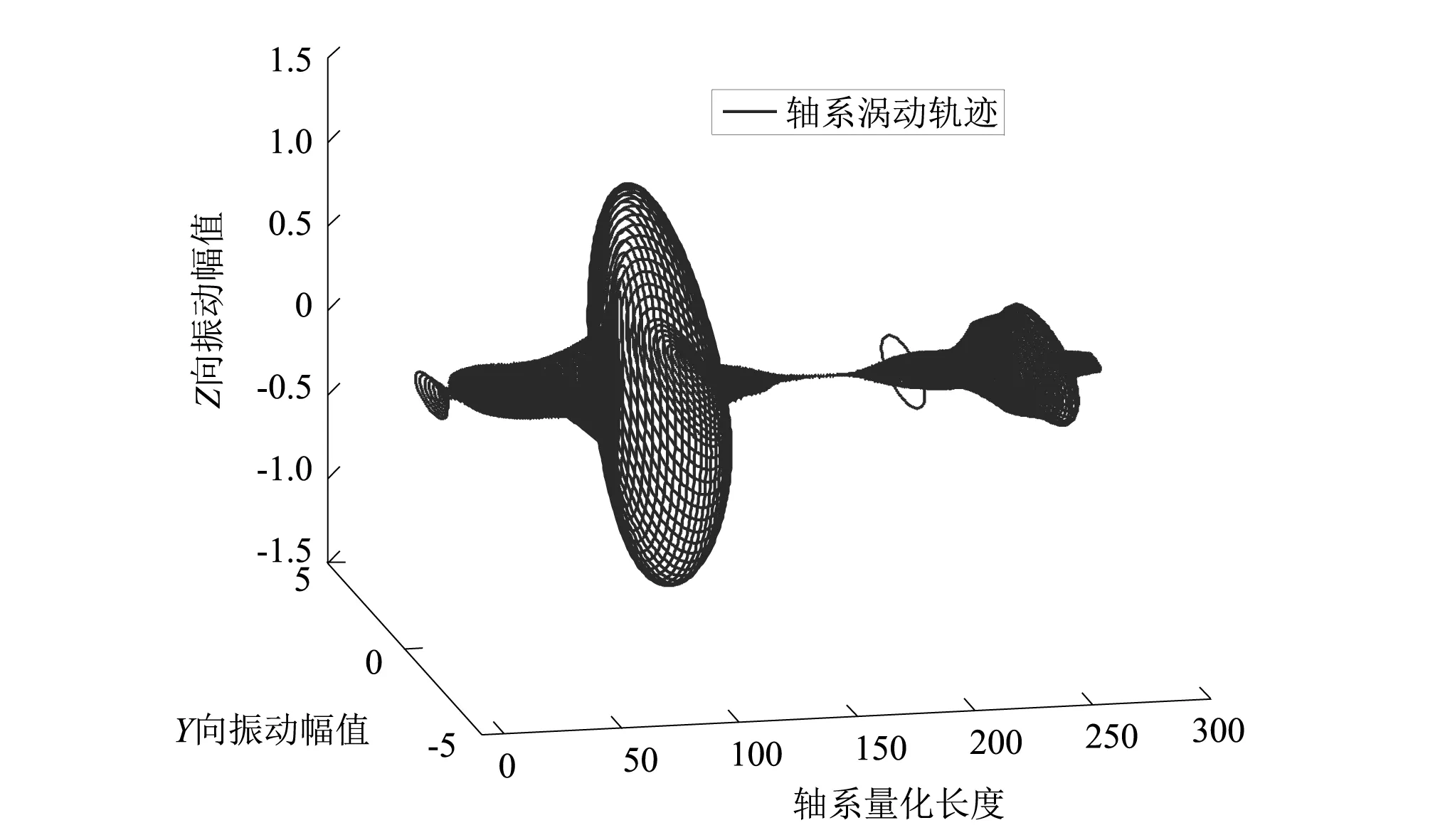
图 20 0.39 Hz时轴系涡动轨迹图Fig.20 0.39 Hz shafting whirl orbit

4 结 语

通过计算不同工况下支撑轴承油膜特性和推力块油膜特性，建立相应的油膜特性矩阵单元，在此基础之上，建立了轴系-基座-壳体系统有限元模型，分析了不同工况下轴系激振力对系统振动特性影响。结果表明，不同工况下，轴承润滑特性不同，尤其是两个艉轴承对于转速敏感度较高，通过轴承传递到壳体上的功率流有差别，在一定程度上会导致船体艉部振动和噪声不同，此外轴系-基座-壳体系统在低频处呈现出许多振动峰值，不同工况也会对其产生影响。通过本文所采用的计算方法，为轴系-基座-壳体耦合振动提供理论依据和计算方法，为研究船体艉部振动和噪音的成因机制和影响规律对于识别和有效控制船体艉部振动和噪声具有重要价值。

[ 1 ] 严新平，李志雄，刘正林，等. 大型船舶推进系统与船体耦合动力学研究综述[J]. 船舶力学，2013，17 (4)： 439-447.

YAN Xinping，LI Zhixiong，LIU Zhenglin, et al. Study on coupling dynamical theory for interaction of propulsion system and hull of large ships: a review[J]. Journal of Ship Mechanics， 2013， 17 (4)： 439-447.

[ 2 ] LEONTOPOULOS C, DOVIES P, PARK K R. Shaft alignment analysis: Solving the reverse problem[J]. Proceedings of the Instituteof Marine Engineering, Science and Technology Part B: Journal of Marine Design and Operations, 2005(8B): 3-12.

[ 3 ] LARSEN O C. Some considerations on shaft alignment of marine shaftings[J]. Norwegian Maritime Research, 1976, 4(2): 19-32.

[ 4 ] 朱军超. 大型船舶轴承支撑状态对轴系振动的影响研究[D]. 武汉： 武汉理工大学，2012.

[ 5 ] 石磊. 计入支承系统特性的船舶推进轴系动态校中研究[D]. 大连： 大连理工大学，2010.

[ 6 ] 李栋梁，谌勇，张志谊. 推力轴承油膜刚度对轴系-艇体结构耦合振动的影响研究[J]. 噪声振动与控制，2009， 29(6)： 81-85.

LI Dongliang, CHEN Yong, ZHANG Zhiyi. Influence of thrust bearing’s oil filn stiffness on the coupled vibration of the shafting ship hull structure[J]. Noise and Vibration Control, 2009, 29(6)： 81-85.

[ 7 ] 刘耀宗，王宁，孟浩. 基于动力吸振器的潜艇推进轴系轴向减振研究[J].振动与冲击， 2009， 28(5)： 184-187.

LIU Yaozong，WANG Ning，MENG Hao. Design of dynamic vibration absorbers to reduce axial vibration of propelling shafts of submarines [J]. Journal of Vibration and Shock， 2009， 28(5)： 184-187.

[ 8 ] 孟浩. 基于声子晶体理论的潜艇推进轴系纵向减振技术研究[D]. 长沙： 国防科技大学，2007.

[ 9 ] 曹贻鹏. 推进轴系引起的艇体结构振动与辐射噪声控制研究[D]. 哈尔滨： 哈尔滨工程大学，2008.

[10] 李良伟，赵耀，陆波，等. 减小船舶轴系纵向振动的动力减振器参数优化[J]. 中国造船，2010， 51(2)： 139-147.

LI Liangwei, ZHAO Yao, LU Bo, et al. Optimization of dynamic absorber parameters for reducing axial vibration of ship shafting[J]. Shipbuilding of China, 2010，51(2)： 139-147.

[11] 赵广. 转子-联轴器-轴承-隔振器系统耦合动力学特性研究[D].哈尔滨： 哈尔滨工业大学，2009.

[12] 杨德庆，罗放，陈静. 有限元功率流落差计算方法研究[J]. 噪声振动与控制，2009，29(6)： 127-131.

YANG Deqing，LUO Fang，CHEN Jin. Power flow level difference finite element analysis[J].Noise and vibration control, 2009, 29(6)： 127-131.

[13] 张志谊，谌勇，李攀硕，等. 轴系-壳体耦合振动控制的试验研究[J]. 现代振动与噪声技术，2009(9)： 65-69.

ZHANG Zhiyi, CHEN Yong, LI Panshuo, et al. Research on the experiment of shaft-hull coupled vibration control[J]. Modern Vibration and Noise Technology, 2009(9)： 65-69.