基于二维互补随机共振的轴承故障诊断方法研究

陆思良， 苏云升， 赵吉文， 何清波, 刘 方， 刘永斌

(1.安徽大学 电气工程与自动化学院，合肥 230601； 2.中国科学技术大学 精密机械与精密仪器系，合肥 230026)

机器部分旋转部件在经过长时间的运行后其轴承会发生磨损等故障，这会导致机器停机乃至整个机械系统瘫痪[1]。多种基于信号处理的方法被广泛用于机械微弱信号特征提取和故障诊断中，例如小波分析[2-3]，经验模态分解[4-5]，随机共振(Stochastic Resonance, SR)[6-7]等。其中，SR能够利用噪声增强微弱周期信号这一独特优点使其被广泛应用于微弱信号检测和轴承故障诊断中。

当前绝大部分的研究都是基于经典的一维随机共振(One-Dimensional SR, 1DSR)模型。1DSR模型虽然能够实现信号增强，但仍存在一些问题，例如1DSR对高频噪声有较好的抑制作用，但不能有效地滤除低频干扰，从而影响轴承故障特征频率(Fault Characteristic Frequency, FCF)的识别和精确诊断。

因此，采用更先进的SR模型用于微弱信号检测成为近年来的研究热点。文献[8-9]提出了一种新型的二维随机共振(Two-Dimensional SR, 2DSR)方法来利用噪声增强微弱的正弦信号。这种新型2DSR模型具有两个输入通道和两个输出通道以及两个耦合参数。相比之下，1DSR只有一个输入和一个输出通道，从这一角度而言，2DSR比传统的1DSR更能精确设计以匹配不同的输入信号从而获得更好的滤波效果。

本文在2DSR的基础上提出一种新的二维互补随机共振(Two-Dimensional Complementary SR, 2DCSR)方法并将其应用到轴承故障诊断中。首先将轴承故障信号根据共振带的位置进行带通滤波并解调，随后将解调信号对半分成两段子信号输入2DCSR的两个输入通道(x和y通道)。通过调整合适的系统参数，y通道的信号将对x通道的微弱周期信号进行有效地增强。

此外，SR是一个信号系统，在输入信号确定的情况下，其输出信号取决于SR系统参数，因此SR需要一个反馈指标引导参数调节。最常用的指标为信噪比，但信噪比的计算需要精确的频率信息，这一要求在工程信号中不一定能够得到满足。为此，本文采用Wang等[10]提出的加权功率谱峭度(Weighted Power Spectrum Kurtosis, WPSK)指标来实现2DCSR参数的自适应调节。

本文所采用的2DSR模型相比传统的1DSR模型具有更高的维度，能够更有效地增强系统中的微弱周期信号，从而能够突出增强轴承FCF以实现高效的轴承故障诊断。仿真信号和实际轴承故障信号对比实验充分验证了该方法的有效性和优越性。

1 二维互补随机共振

1.1 模型

2DCSR模型可由以下一阶偏微分方程组表示：

(1)

式中dωx(t,t>0)表示维纳过程并满足：①dωx(t,t>0)是关于t连续的独立增量过程；②对于任意t和τ，dωx(t)-dωx(τ)～N(0,1)服从标准正态分布。该维纳过程也是零均值、单位方差的加性高斯白噪声的积分形式。dωy(t)是和dωx(t)定义一致但相互独立的维纳过程。εx和εy为噪声强度值，输入信号是两个具有相同频率ω和不同幅值A1,A2的正弦信号。其中，二维势阱函数U(x,y)表示为：

(2)

式中：a和b是两个正实数，δ是二维模型中的耦合参数。因此，式(1)又可以表示为：

(3)

由于x和y通道都具有输入和输出，考虑到系统的两个输入信号不同，为使滤波效果最优化，将式(3)中的耦合参数δ分别设置成δ1和δ2两个独立的耦合参数。式(3)进一步改写为：

(4)

进一步地，定义一个实数k> 0，对2DSR模型做以下参数代换：

(5)

(6)

(7)

(8)

(9)

式(4)可以表示成：

(10)

式中：TR1和TR2是时间尺度变换因子，SR1和SR2是空间尺度变换因子。考虑到在实际系统中，输入信号已经同时包含了微弱周期信号分量和噪声，因此进一步定义系统的两个输入信号为S1(t)和S2(t)：

(11)

式中：f0表示两个同频微弱周期信号的频率；φ1和φ2分别为两个输入信号的相位。

图1 2DCSR的模型图Fig.1 2DCSR model

1.2 WPSK反馈指标

由图1可见，对于确定的输入信号S1(t)和S2(t)，2DCSR的输出取决其系统参数，因此需要一个反馈指标来调整2DCSR系统参数使其输出最优化。大部分SR的研究都用信噪比作为调节指标，但信噪比计算需要精确的频率信息，这在实际信号中不一定能够满足。为解决此问题，本文采用WPSK指标来自适应地调整优化2DCSR的系统参数。WPSK指标为功率谱峭度(Power Spectrum Kurtosis, PSK)和相关系数(Correlation Coefficient, CC)的乘积。

PSK定义的是功率谱序列的峭度值。2DCSR的M点离散输出信号为x[n],n= 1, 2, 3,…,M。通过快速傅里叶变换(Fast Fourier Transform, FFT)可得到x[n]的功率谱px[n],n= 1, 2, 3,…,M。则PSK可由以下公式计算：

(12)

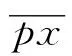
除了PSK之外，还需要另一个指标CC来衡量输出信号的规则程度。假设fm和φm是px[n]中能量最高的谱线的频率和相位，构造一个正弦信号：

h[n]=sin(2πfmt[n]+φm)

(13)

式中：t[n]=0, 1/fs, 2/fs,…, (M-1)/fs为离散时间序列，fs为信号采样频率，则CC可由下式计算：

(14)

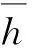
WPSK=|CC|×PSK

(15)

WPSK衡量了2DCSR的滤波效果和输出信号的规则程度，且该指标具有自适应性，即不需要事先知道驱动频率的信息就能实现参数的自适应寻优。

1.3 方法总结

对于确定的输入信号，2DCSR的输出由系统的6个参数确定，这6个参数采用WPSK指标进行优化以得到最优的输出结果，方法实施流程图如图2所示，具体步骤如下：

(1)信号预处理。对采集的轴承故障信号进行预处理，例如带通滤波和共振解调。

(2)系统参数初始化。初始化2DCSR模型的6个参数SR1,SR2,TR1,TR2,δ1和δ2的寻优范围和步增间隔，即划分了网格。

(3)输出信号计算分析。将一段信号对中拆分成两个输入子信号S1(t)和S2(t)，采用遍历搜索方法依次调整模型参数，分别得到6个维度的2DCSR结果x(t)和y(t)，计算x(t)的WPSK值。

(4)输出效果评价。在6维的WPSK矩阵中检查WPSK的最大值及对应的6个最优参数集，如果最优参数位于寻优范围的边界，则扩展相应参数的范围，返回步骤(3)；否则，进入步骤(5)。

(5)信号后处理。获得WPSK值最高的输出信号为最优滤波信号，通过检验FCF识别轴承故障。

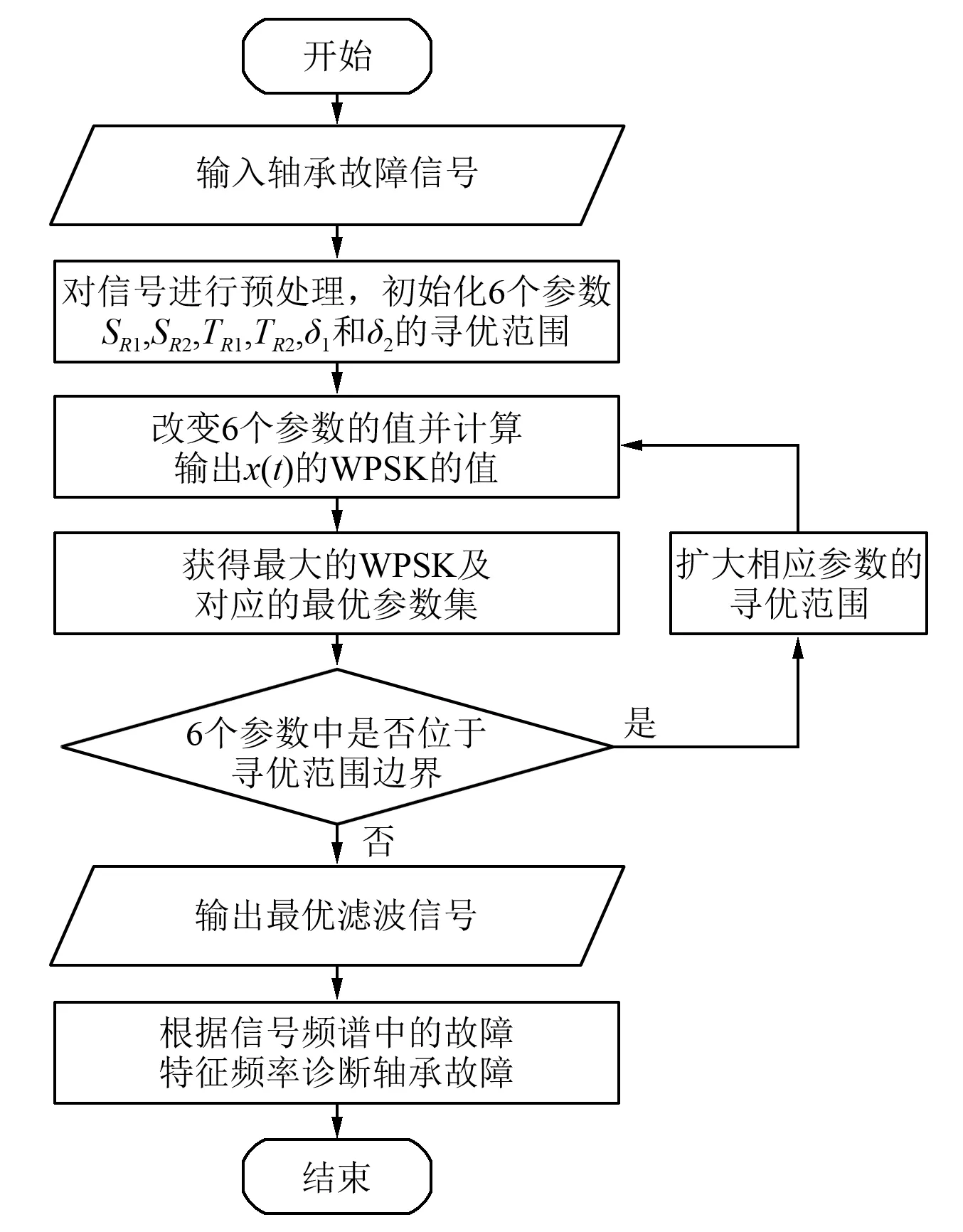
图2 2DCSR算法流程图Fig. 2 Algorithm flowchart of the 2DCSR method

2 数值仿真

为了验证本文方法的有效性和优越性，本章采用MATLAB/SIMULINK搭建2DCSR模型进行数值仿真分析并和传统的1DSR方法作比较。1DSR的模型如下：

(16)

式中：g和k为一维双稳态势阱参数，S(t)=[S1(t)S2(t)]为含噪输入信号，即2DCSR的输入S1(t)和S2(t)实际上由S(t)对半拆分而得。式(16)可以通过4阶龙格库塔方程求解，通过调整合适的步长h以及双稳态势阱参数g和k使得WPSK最大，即可得到最优的1DSR输出信号，具体步骤参见文献[11]。

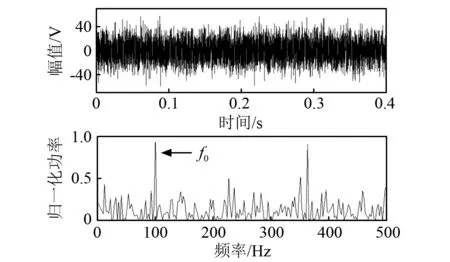
图3 含噪正弦信号及其功率谱Fig. 3 Noisy sinusoidal signal and its power spectrum

3 工程应用

为进一步验证2DCSR方法在轴承故障微弱信号检测的有效性，分别对轴承内圈故障和外圈故障信号进行处理和分析。轴承内圈故障信号来自美国的凯斯西储大学(CWRU)的轴承数据中心网站[12]，轴承外圈故障信号来自实验室自制的轴承故障试验台。轴承的参数及故障信息，如表1所示。

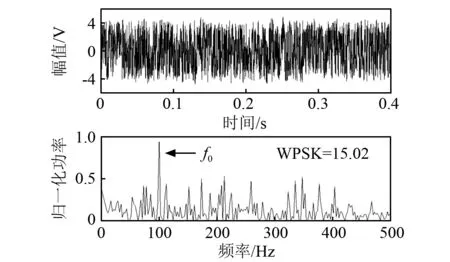
图4 1DSR最优输出信号及其功率谱Fig. 4 1DSR optimal output signal and its power spectrum

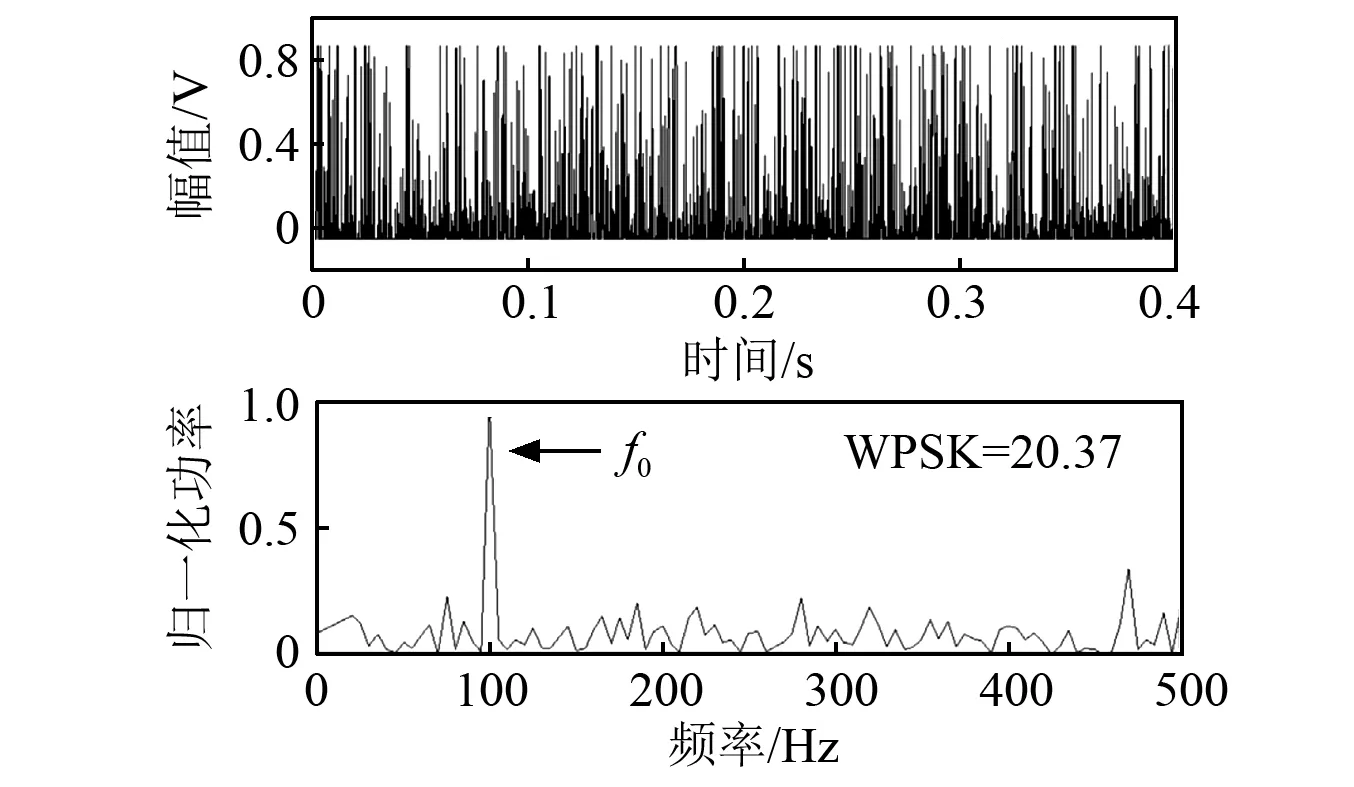
图5 2DCSR最优输出信号及其功率谱Fig. 5 2DCSR optimal output signal and its power spectrum

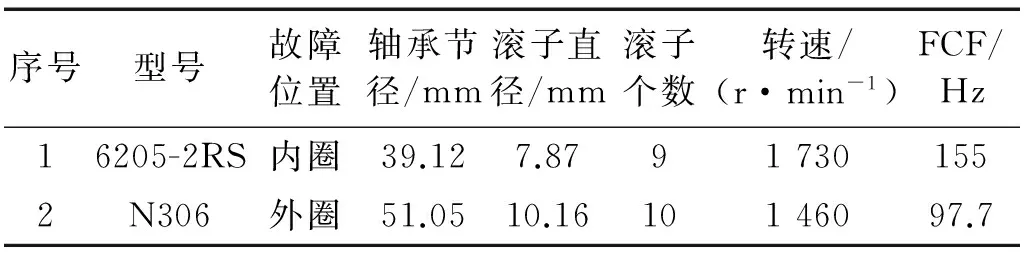
表1 轴承参数及故障信息

3.1 内圈故障检测

首先对轴承内圈故障信号进行分析。轴承内圈具有局部故障时，运动的滚子会依次通过内圈故障部位并碰撞产生冲击振动，冲击振动进一步引起机器共振，因此轴承故障信号由一系列共振频率调制的衰减冲击信号构成。另一方面，在一定转速下，两个相邻冲击信号的时间间隔(其倒数即为故障特征频率)能够反映轴承不同的故障类型。由于故障信号是调幅信号，因此共振解调技术常用于解调故障信号从而能够在解调(包络)谱中发现故障特征频率[13]。

信号经过带通滤波和包络解调后，其包络信号和包络谱如图6所示。时域的包络信号反应了冲击振动序列的轮廓，从轮廓中可见伴有明显噪声干扰的一系列的冲击脉冲。从包络谱中可以辨认出旋转频率fr和内圈故障频率fi，但其它噪声分量十分明显，从而影响轴承故障的精确诊断。将包络信号输入1DSR系统，在最优参数g=4.8,k=15,h=0.3条件下，1DSR的最优输出信号及频谱如图7所示。从时域信号中可见，相对于图6，在SR的作用下部分噪声干扰得到了一定程度的抑制。但频域中fr到fi频段的噪声不能被有效滤除。实验结果表明1DSR对高频噪声的滤波效果较好，对低频噪声的滤波效果有限[14]。随后，采用本文提出的2DCSR方法对包络信号进行处理。利用WPSK作为参数调节指标得到最优的参数为δ1=8.0E+006,δ2=10,SR1=9.0E+005,SR2=10,TR1=1.0,TR2=1.0，和最优输出信号及频谱如图8所示。在2DCSR的框架下，y通道的信号有效地增强了x通道的微弱信号，因此故障特征频率fi在频谱中十分突出，相比之下噪声分量则十分微弱。

图6 轴承内圈故障包络信号及其功率谱Fig. 6 Bearing inner raceway fault envelope signal and its power spectrum

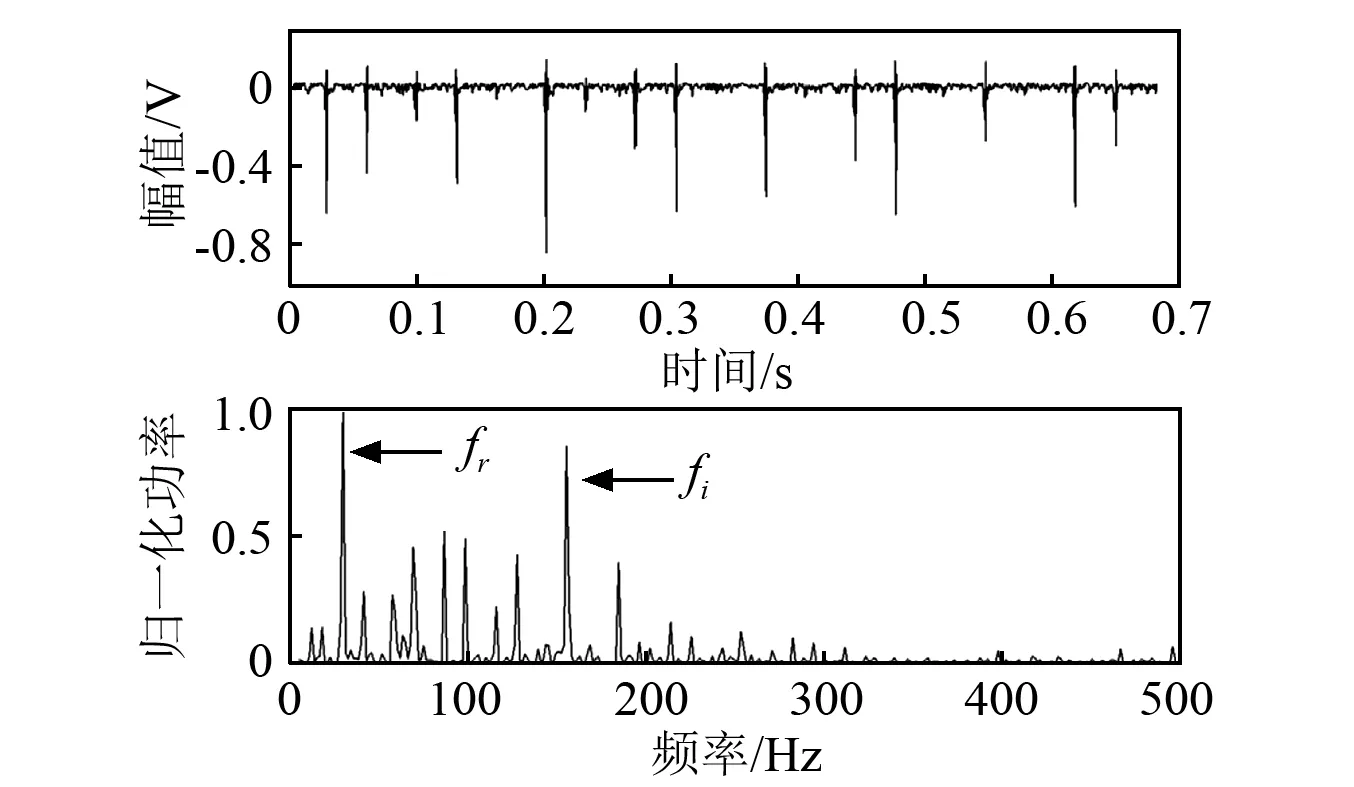
图7 1DSR最优输出信号及其功率谱(内圈故障信号)Fig. 7 1DSR optimal output signal and its power spectrum (inner raceway fault signal)

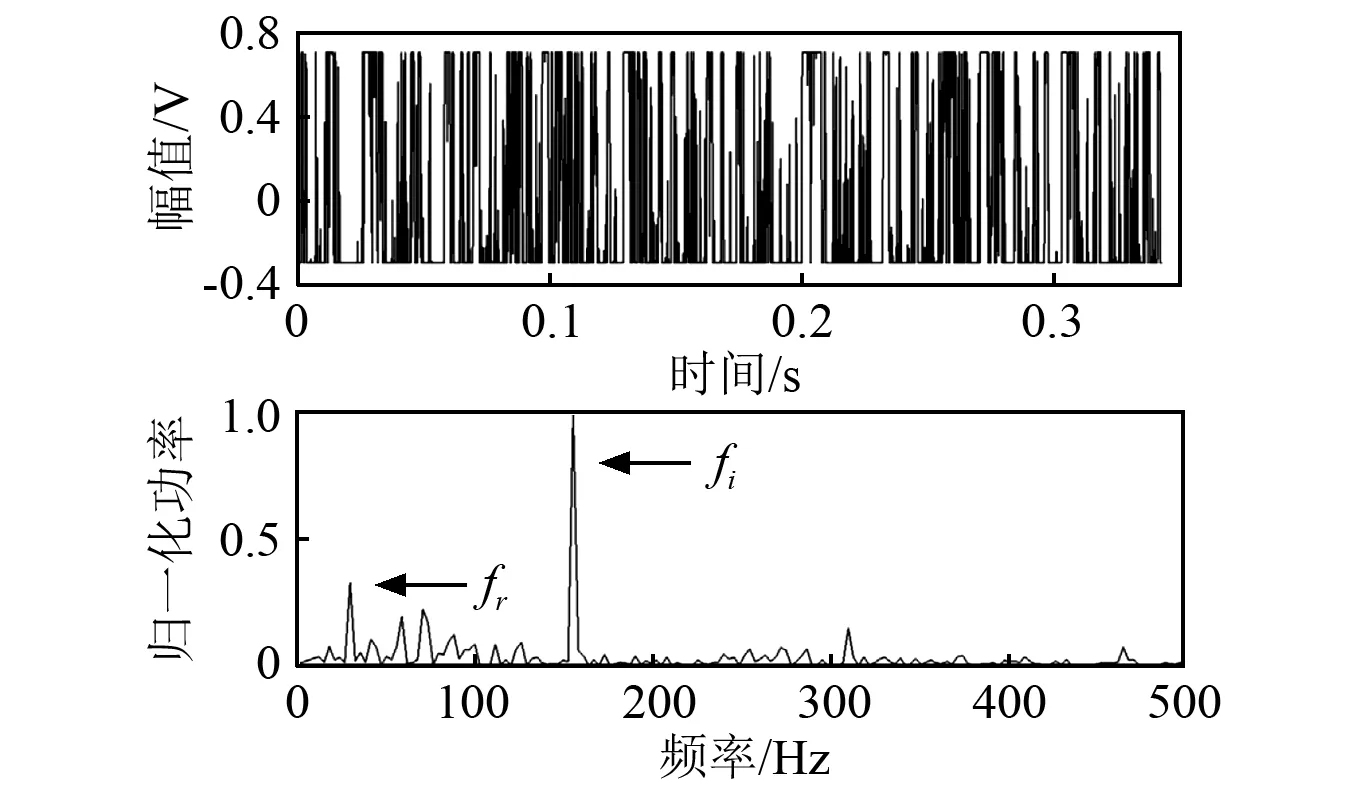
图8 2DCSR最优输出信号及其功率谱(内圈故障信号)Fig. 8 2DCSR optimal output signal and its power spectrum (inner raceway fault signal)

3.2 外圈故障检测

为了进一步验证本文提出方法的优越性和有效性，本节对轴承外圈故障信号进行分析，结果如图9～图11所示。从图9中可见，轴承外圈故障特征频率fo周围的噪声十分明显，干扰对轴承故障的精确诊断。1DSR的最优输出如图10所示，最优参数为：g=5,k=20,h=0.2。从频谱图中可见，高频噪声的能量明显降低，但部分低频噪声的能量反而升高，这一结果再次验证了1DSR的低通滤波特性。2DCSR的结果输出如图11所示，最优参数为：δ1=-7.9E+004,δ2=1.0E+009,SR1=4.0E+004,SR2=1.0E+007,TR1=1.0,TR2=1.0。相比图10，2DCSR的输出频谱中高频和低频噪声能量进一步降低，故障特征频率fo得到有效增强，从而能够明确判断轴承外圈存在故障。通过以上两个工程应用案例，本文提出的2DCSR方法展现出了更好的微弱信号增强效果，从而利于轴承故障的精确诊断。

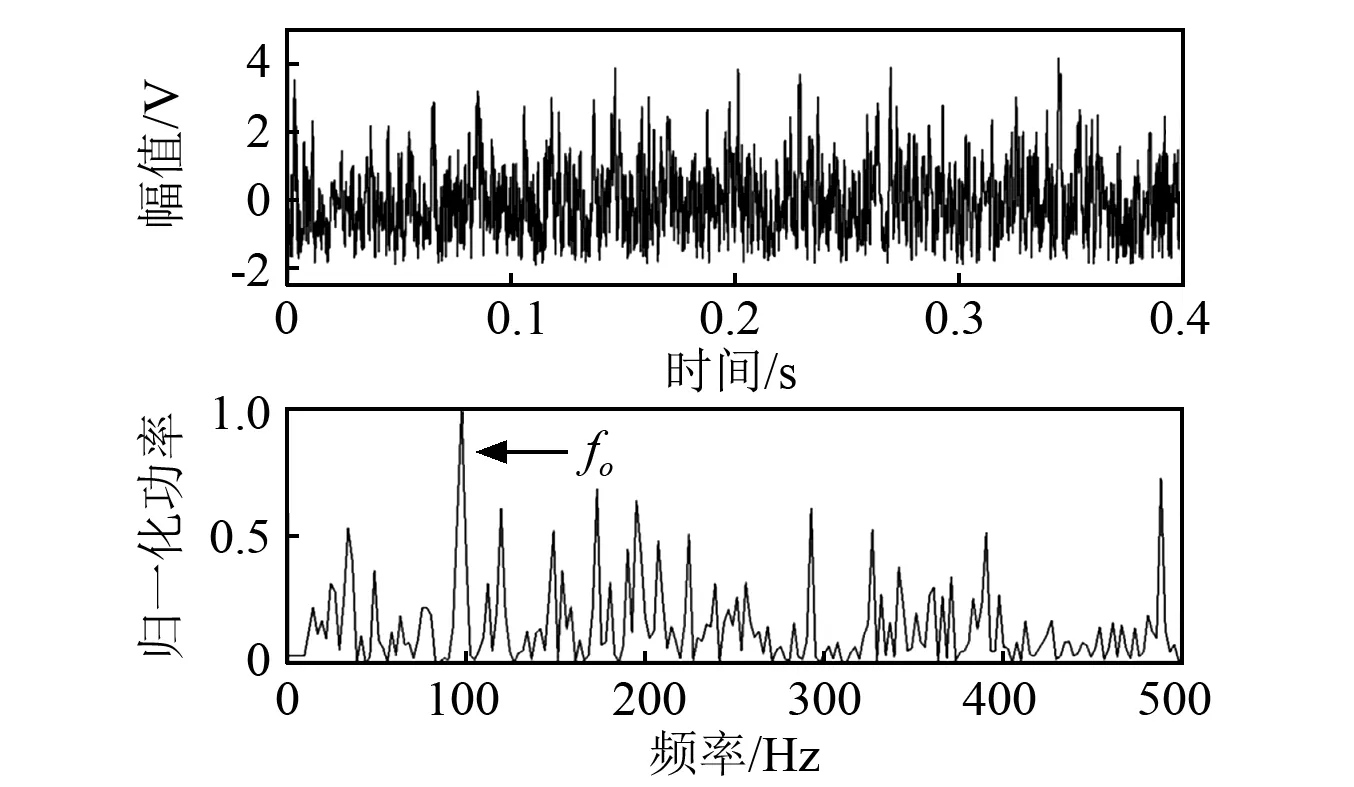
图9 轴承外圈故障包络信号及其功率谱Fig. 9 Bearing outer raceway fault envelope signal and its power spectrum

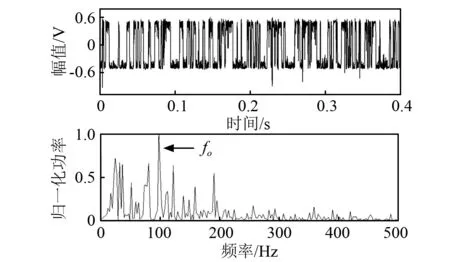
图10 1DSR最优输出信号及其功率谱(外圈故障信号)Fig. 10 1DSR optimal output signal and its power spectrum (outer raceway fault signal)

图11 2DCSR最优输出信号及其功率谱(外圈故障信号)Fig. 11 2DCSR optimal output signal and its power spectrum (outer raceway fault signal)

3.3 定量分析

从3.1和3.2节的定性分析可见，2DCSR方法比1DSR具有更好的滤波效果。这两种方法都采用WPSK指标自适应地调整参数以达到最优滤波效果。WPSK的值越高表示信号的噪声干扰越小，也即输出信号越干净。以上两个案例采用不同方法得到的最大WPSK值如表2所示。可见，2DCSR方法处理轴承内圈和外圈故障信号的WPSK值明显都高于1DSR方法，因此该定量分析结果再次验证了本文提出方法的优越性。

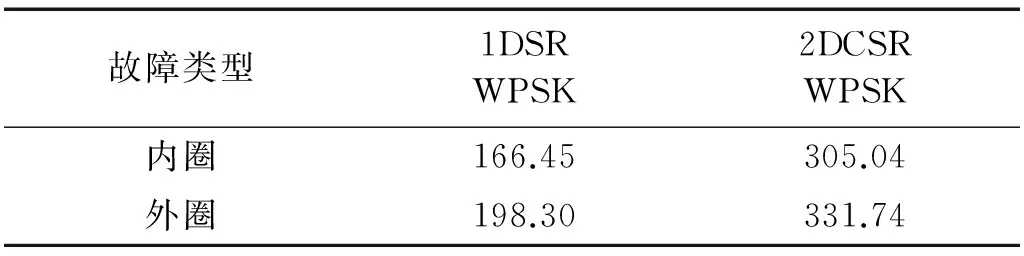
表2 输出信号的WPSK值

3.4 讨论

考虑到本文主要研究2DCSR系统的信号增强效果，因此采用简单的网格划分和遍历搜索方法来获得2DCSR的6维最优参数。为了提高参数的搜索效率，可以考虑在2DCSR方法中引入人工鱼群算法、遗传算法[15]等智能优化方法，这方面工作将在后续研究中开展。

4 结 论

针对工程中的微弱信号检测问题，本文提出一种2DCSR方法并将其应用于轴承微弱信号的增强和故障诊断。2DCSR方法基于2DSR模型，通过将信号对半拆分成两个频率相同，噪声和相位不同的子信号并输入系统的x和y两个通道，采用自适应指标WPSK指引系统参数的调整，使得x通道的信号在y通道的不同相位的微弱周期信号和噪声协助下得到增强，从而实现x通道的微弱信号增强检测。仿真含噪信号和实际轴承微弱故障信号的实验结果验证了本文提出的2DCSR比传统的1DSR具有更明显的微弱信号检测效果，尤其是在强背景噪声的情形下，2DCSR具有更优越的高频和低频噪声抑制能力。因此，2DCSR方法有望应用于机械故障微弱信号的增强诊断和其它涉及到微弱周期信号检测的领域。

[ 1 ] 项巍巍, 蔡改改, 樊薇, 等. 基于双调Q小波变换的瞬态成分提取及轴承故障诊断应用研究 [J]. 振动与冲击, 2015, 34 (10): 34-39.

XIANG Weiwei, CAI Gaigai, FAN Wei, et al. Transient feature extraction based on double-TQWT and its application in bearing fault diagnosis [J]. Journal of Vibration and Shock, 2015, 34(10): 34-39.

[ 2 ] 严如强, 钱宇宁, 胡世杰, 等. 基于小波域平稳子空间分析的风力发电机齿轮箱故障诊断 [J]. 机械工程学报, 2014, 50 (11): 9-16.

YAN Ruqiang, QIAN Yuning, HU Shijie, et al. Wind turbine gearbox fault diagnosis based on wavelet domain stationary subspace analysis[J]. Journal of Mechanical Engineering, 2014, 50 (11): 9-16.

[ 3 ] YAN R Q, GAO R X, CHEN X F. Wavelets for fault diagnosis of rotary machines: A review with applications [J]. Signal Processing, 2014, 96: 1-15.

[ 4 ] 郑近德, 程军圣, 杨宇. 改进的 EEMD 算法及其应用研究 [J]. 振动与冲击, 2013, 32 (21): 21-26.

ZHENG Jinde， CHENG Junsheng， YANG Yu, Modified EEMD algorithm and its applications [J]. Journal of Vibration and Shock, 2013, 32 (21): 21-26.

[ 5 ] LEI Yaguo, LIN Jing, HE Zhengjia, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery [J]. Mechanical Systems and Signal Processing, 2013, 35 (1/2): 108-126.

[ 6 ] 朱维娜, 林敏. 基于人工鱼群算法的轴承故障随机共振自适应检测方法 [J]. 振动与冲击, 2014, 33 (6): 143-147.

ZHU Weina，LIN Min. Method of adaptive stochastic resonance for bearing fault detection based on artificial fish swarm algorithm [J]. Journal of Vibration and Shock, 2014, 33 (6): 143-147.

[ 7 ] 冷永刚, 田祥友. 一阶线性系统随机共振在转子轴故障诊断中的应用研究 [J]. 振动与冲击, 2014, 33 (17): 1-5.

LENG Yonggang, TIAN Xiangyou. Application of a first-order linear system's stochastic resonance in fault diagnosis of rotor shaft [J]. Journal of Vibration and Shock, 2014, 33 (17): 1-5.

[ 8 ] BARBINI L, COLE M O T, HILLIS A J, et al. Weak signal detection based on two dimensional stochastic resonance [C]. IEEE 23rd European Signal Processing Conference (EUSIPCO), 2015: 2147-2151.

[ 9 ] BARBINI L, BORDI I, FRAEDRICH K, et al. The stochastic resonance in a system of gradient type [J]. The European Physical Journal Plus, 2013, 128 (2): 1-12.

[10] WANG Jun, HE Qingbo, KONG Fanrang. Adaptive multiscale noise tuning stochastic resonance for health diagnosis of rolling element bearings [J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64 (2): 564-577.

[11] LU Siliang, HE Qingbo, KONG Fanrang. Effects of underdamped step-varying second-order stochastic resonance for weak signal detection [J]. Digital Signal Processing, 2015, 36: 93-103.

[12] CWRU. http:∥csegroups.case.edu/bearingdatacenter/pages/download-data-file.

[13] LU Siliang, HE Qingbo, KONG Fanrang. Stochastic resonance with Woods-Saxon potential for rolling element bearing fault diagnosis [J]. Mechanical Systems and Signal Processing, 2014, 45 (2): 488-503.

[14] LU Siliang, HE Qingbo, ZHANG Haibin, et al. Enhanced rotating machine fault diagnosis based on time-delayed feedback stochastic resonance [J]. Journal of Vibration and Acoustics-Transactions of the ASME, 2015, 137: 051008.

[15] HE Qingbo, WANG Jun, HU Fei, et al. Wayside acoustic diagnosis of defective train bearings based on signal resampling and information enhancement [J]. Journal of Sound and Vibration, 2013, 332: 5635-5649.