基于频谱包络曲线的稀疏自编码算法及在齿轮箱故障诊断的应用

张绍辉， 罗洁思

(厦门理工学院 机械与汽车工程学院，福建 厦门 361024)

齿轮箱作为旋转机械中必不可少的连接和传递动力的重要零部件，在机床、航空、农业机械、运输机械等现代工业设备中得到了广泛的应用。由于齿轮箱结构复杂，工作环境恶劣，非常容易出现故障，其运行状态将直接影响到整个设备传动组的工作性能、加工精度和生产效率。因此，齿轮箱故障识别及分类是理论界和工业界共同关注的热门课题[1]。

机械设备故障识别及分类方法可以分为：基于解析模型、基于信号处理和基于知识处理等三大类方法。其中前两种方法在很大程度上依赖于专家经验的指导，而基于知识处理的方法属于智能诊断技术，从故障信息的检测到特征提取、从状态识别到故障分析和干预决策等都实现知识的引导，使诊断技术不仅为少数专业人员所掌握，而且也成为一般人员也能使用的工具。传统的智能诊断方式如，主成分分析(Principal Component Analysis，PCA)、局部保持投影映射(Locality Preserving Projections，LPP)等已应用于机械设备的状态识别并取得了一定的成果[2-3]。然而，从算法的结构分析，这些智能处理技术的结构均被认为是属于“浅层模式”，该模式的主要缺点在于：①不能完整的描述输入信息的真实情况，揭示复杂输入的内在规律；②这些算法针对的是经过特征计算之后的数据结构，需要通过专家经验对时域信号预先进行时域、频域及时频域特征计算，才能较好的区分不同状态类型。

由于传统智能诊断技术的以上局限性，限制了算法的推广，泛化性能差。针对该问题，Hinton提出的深度学习算法(Deep Learning, DL)等[4-5]能够有效的揭示复杂输入的内在规律，具备提取样本数据集本质特征的强大能力，引起了理论界与商业界关于深度学习算法研究的热潮。Bengio等[6-7]提出了受限玻尔兹曼机，贪婪逐层深度网络结构等用于机器视觉，图像处理；百度在2013年成立了深度学习研究院[8]，致力于研究深度学习技术在图像语音处理方面的应用；微软发起的Adam项目[9]证明大规模商用分布式系统能有效训练巨型深层神经网络。

从现有的检索资料显示，已经有学者将深度学习理论应用于机械故障诊断中。如Tamilselvan等[10]利用深度置信网络融合多传感器信息，用于航空发动机及电力变压器的故障分类；Tran等[11]则利用深度置信网络融合振动、压力与电流等三种信号对往复式压缩机阀门的故障进行分类识别；Fu等[12]将深度置信网络用于切削设备的状态监测；Hu等[13]将降噪稀疏自编码用于风机转速预测；Gan等[14]构建基于深度置信网络的分层故障诊断模型用于轴承状态识别；王宪保等[15]将深度置信网络方法应用于太阳能电池片表面缺陷检测；黄海波等[16]将深度置信网络用于车辆悬架减震器异响的分类；赵旻昊[17]将深度置信网络用于浮式储油卸油装置的状态监测；雷亚国等[18]将深度学习算法用于行星齿轮箱健康监测；谢吉朋[19]将深度置信网络用于列车走行部件的故障诊断。从现有的文献中发现，大部分的方法直接将时域信号或者频域信号作为低层数据集输入到深度学习模型当中以减弱专家的经验影响，提高算法的泛化能力。

然而，对于时域信号的截取需要考虑不同样本之间信号的一致性，即同类样本的时域信号需要具有一定的相似度，否则，将导致异类样本之间的混叠，而频域信号可以描述样本的频域特征，不同样本的频域特性存在差异，因此，采用频域输入能够有效保证同类样本之间的相似度。但是，为了获得较好的频域分辨率以取得良好的识别效果，频域信号的样本长度较大，导致深度学习模型输入层的计算量较大，影响学习算法在设备状态诊断的效率。针对该问题，对采集到的时域信号进行频谱转化，使得同类样本之间具有一定的相似度，同时为了提高计算效率，对频谱成分提取包络线信息，获得频域信号的主要变化形态，得到的包络线成分的数据长度远小于频域信号的长度，由此实现提高深度学习计算效率的同时，保证识别效果。将该方法与稀疏自编码结合用于齿轮箱状态诊断，实验证明该方法能够有效的提高深度学习算法的计算效率及识别效果。

1 稀疏自编码算法原理

稀疏自编码是一种无监督算法，通过对输入数据的编码(encode)和解码(decode)过程，使得输出与输入最大程度的相似，即得到表征输入数据的隐含层特征，从而达到降维及提升数据分类效果的目的，模型示例如图1所示。

假设第i层的输入为Bi，相应的输出为Bi+1(即为第i+1层的输入)，则有如下公式：

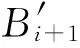
(1)

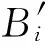
(2)

式中第一项和第二项为编码过程，第三项为解码过程，当i=0时，B0=A，λ用于控制稀疏惩罚项的相对重要性，|Bi+1|1为L1范数，用于控制输出的稀疏程度，防止对输入数据的过度拟合，σ为Sigmoid函数，公式如下：

(4)

稀疏自动编码通过迫使隐含层节点的稀疏化，使得隐含层中只有少量的点处于激活状态，减弱了隐层节点特征同质化问题，具有较好的鲁棒性。

稀疏编码的无监督过程只能保证高层输出与低层输入尽可能的一致，高层输出还不具备相应的识别分类能力，因此，为了引导稀疏算法实现自动的分类过程，在高层输出与样本的标签之间构建映射转换关系，并根据标签转换误差实现整个流程的微调，即为后向微调过程。

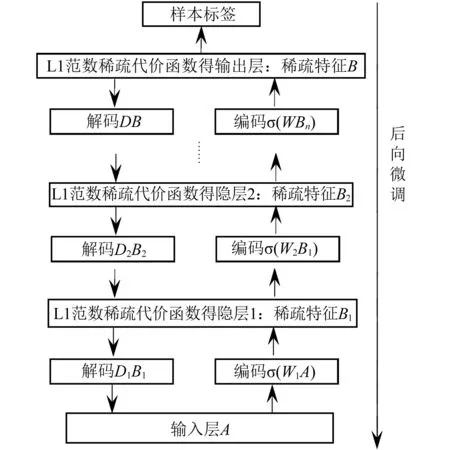
图1 稀疏自动编码器算法原理流程Fig.1 The flow chart of sparse autoencoder

2 所提方法的实现原理

对频域做包络线的实质就是将频域信号分为若干子模块，将每个子模块的峰值点相连，获得该频域信号的变化态势，此时，包络线的数据长度为子模块的个数，远小于频域点数。对于同类样本，其故障主要频率成分相同，频域的包络线应有良好的一致性，而异类样本的包络线存在一定的差别。因此，对频域信号取包络线可以从一定程度上提高后续诊断模型的识别及聚类效果。

假设采集到的原始数据集X={x1,x2,…,xn}为n×m的矩阵，其中n为样本数，m为原始数据频域长度，稀疏自编码第一隐含层的特征数为d，循环次数为k，为了提高计算效率且保证样本类别信息的一致性，对每个样本的频域数据取包络线，具体做法如下，

(1)将原始数据集的每个样本xi(i=1,2,…,n)长度m均分为h个子模块，即xi={xi1,xi2,…,xih}；

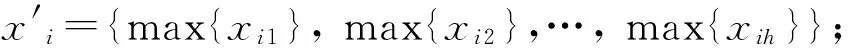
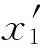
对于原始数据集X在第一隐含层需要构建的编码权重和解码权重矩阵分别为：m×d和d×m，因此，原始数据集在第一隐含层的计算复杂度为：2×n×k×m×d，而对于所提包络特征预处理方法所需要的计算复杂度为：2×n×k×m×h，远小于原始数据处理方法，第一隐含层特征数越大，这种区别越明显(第一隐含层之后两者的计算复杂度相同，与隐含层的特征数相关)。具体实现流程如图2所示。

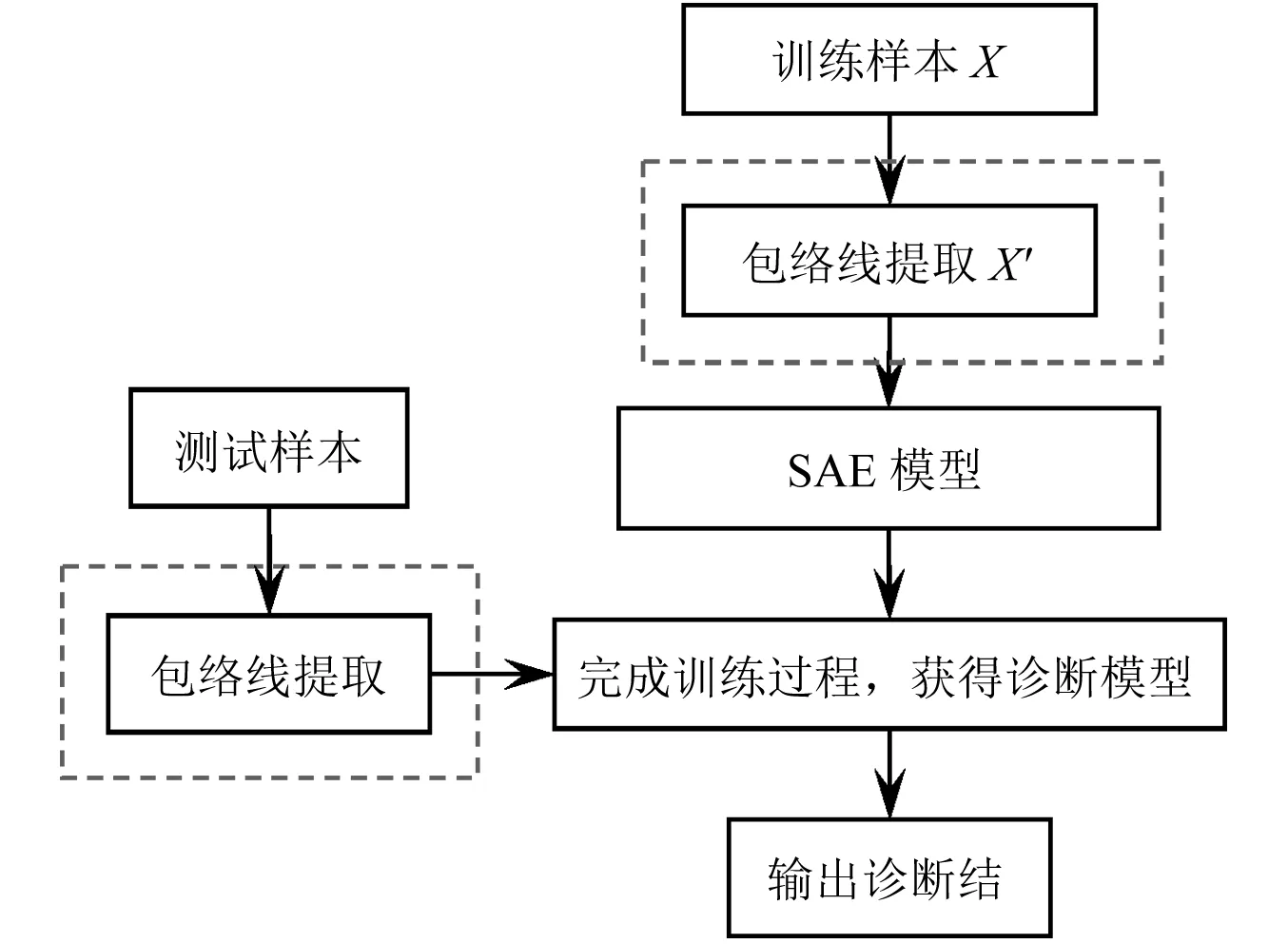
图2 基于包络特征的稀疏自编码诊断流程Fig.2 The process of sparse autoencoder diagnosis based on envelope characteristic

3 仿真与实验分析

3.1 仿真数据

实际机械设备的状态信号受到各种噪声的干扰，增加故障诊断的难度，为了研究所提方法在噪声干扰下的识别效果，设置轴承仿真信号如公式(5)所示[20]，在仿真信号中添加0 db的高斯白噪声(图3为时域信号，图4为相应的频谱)，对比所提方法在噪声干扰下的识别效果。从时域及频域图可以看出，在噪声的干扰下，冲击幅值0.5与正常状态信号及其相似，冲击幅值为1时的频谱亦被噪声所干扰，频率特征不明显，很难从时域或者频域中区分。

y(t)=yd(t)yq(t)yr(t)ye(t)+yn(t)

(5)

式中：yd为故障的冲击信号；yq为载荷分布信号；yr为轴承共振处的频率信号；ye阻尼衰减信号；yn为噪声。设定轴承的转速为1 100 r/min，采样频率为8 kHz。每类轴承状态的样本数为120，数据长度为8 192。对该数据集按照以下两种方式输入稀疏自编码模型，方式 1：对每个频谱信号分为256个子模块，连接每个子模块的峰值点，获得包络线，以该包络线为新的数据集：480×256，将其输入诊断模型；方式 2：频域数据直接输入模型：480×8192。选取12.5%、25%、37.5%、50%、62.5%的样本用于训练SAE模型，全体数据集作为测试样本。对比方式1和方式2构建的诊断模型对测试样本的识别正确率、聚类效果Jb[21]及F系数(识别正确率和聚类效果Jb的平均，是对系统整体性能的评价)，验证所提方法的有效性。设置4种深度层数及相应的隐含层特征数分别为：空隐含层、单隐含层：80、双隐含层：80-50、三隐含层：80-50-20。为了实现低维聚类的可视化，设定高层输出维数为3。

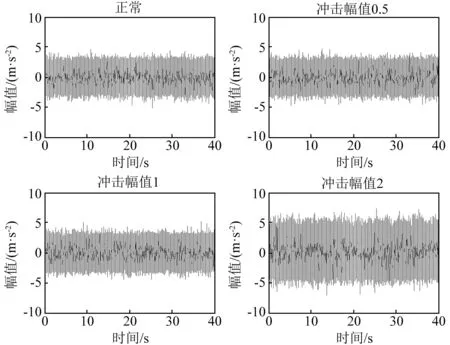
图3 添加0 db高斯白噪声的时域波形Fig.3 The time signal wave by add 0 db white gaussian noise

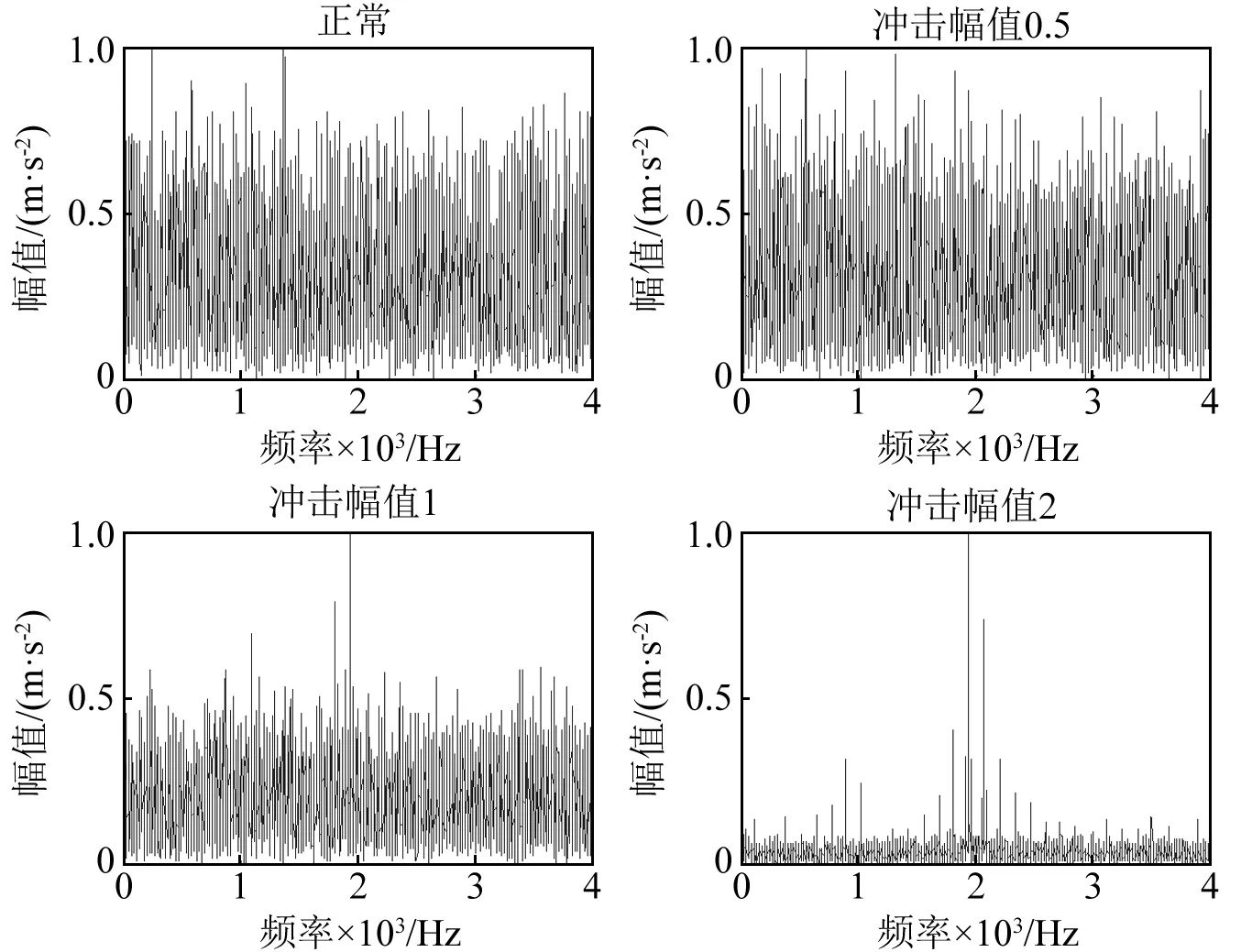
图4 添加0 db高斯白噪声的频域波形Fig.4 The demodulation spectrum by add 0 db white gaussian noise

对比图5、图6、图7的识别正确率、聚类指标Jb及综合指标F可见，在强噪声的干扰下，所提包络线方法在0隐含层、1隐含层、2隐含层和3隐含层下的识别正确率可以达到0.8以上(隐含层数为1，训练样本数为25%时为0.81；隐含层数为2，训练样本数为62.5%时为0.85；隐含层数为3，训练样本数为25%时为0.83)，优于原始无包络线方法。聚类指标Jb值采用原始方式能取得较优结果。

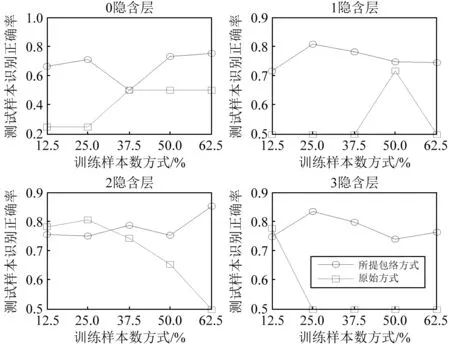
图5 两种方式在不同深度层数的识别正确率Fig.5 The recognition accuracy of two algorithms under different deep levels

图6 两种方式在不同深度层数的聚类评价指标Jb值Fig.6 The Jb value of two algorithms under different deep levels

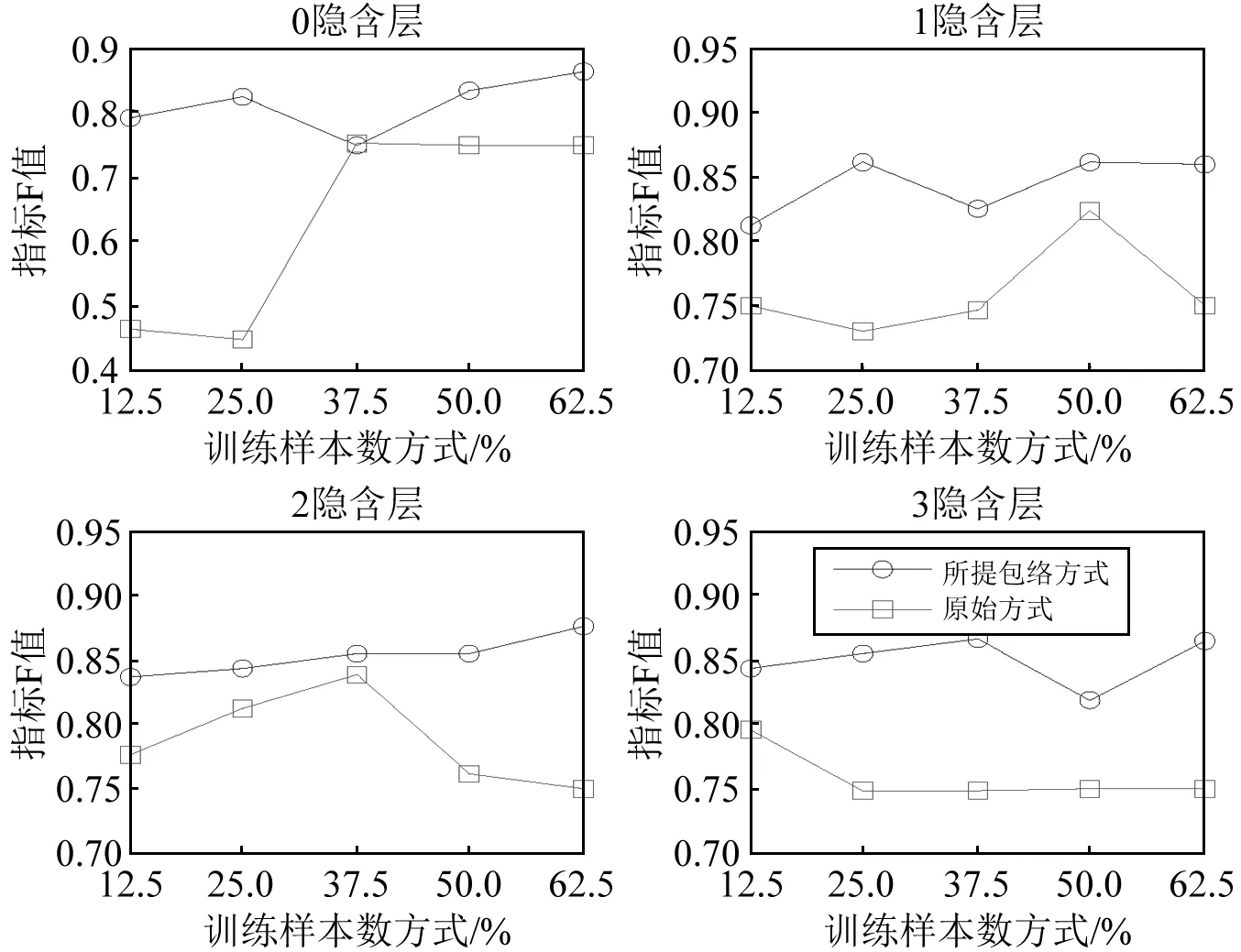
图7 两种方式在不同深度层数的指标F值Fig.7 The F value of two case under different deep levels

由图7的综合评价指标F值可见，所提包络线方式在4种隐含层模式及5种测试样本数下均明显大于原始方式，取得较好识别效果，而且此时所提方法的维数仅为原始方式的1/32，具有较好的计算效率。

3.2 实验数据

齿轮箱故障诊断传动试验台、传感器布置及齿轮箱传递路线如图8所示，二挡传递路线为：输入轴-齿轮26—齿轮38—齿轮20—齿轮41—输出轴；五挡传递路线为：输入轴-齿轮26—齿轮38—齿轮42—齿轮22—输出轴，故障轴承均放在输出轴位置。图9为具体故障轴承和齿轮，分别为：轴承内圈线切割故障、齿轮断齿，其中内圈故障程度为线切割宽度为0.2 mm，深度为0.5 mm。实验齿轮箱运行状态设置分为：①正常状态；②单一故障状态：内圈故障、二挡剥落、五档断齿；③复合故障状态：内圈故障+二挡剥落、内圈故障+五档断齿，共6种齿轮箱状态，即数据样本的类别数为6。通过振动加速度传感器采集这些状态在转速为1 000 r/min和1 250 r/min，载荷为0 Nm和50 Nm四个工况下的时域信号，采样频率为24 kHz，采样时间为0.5 s，采集每种工况120次，并做快速傅里叶变换，则每类齿轮箱状态的样本数为480。因此，共得到齿轮箱状态样本数据矩阵为2 880×6 140，其中2 880为样本数，6 140为样本维数。

对该数据集按照以下两种方式输入稀疏自编码模型，方式 1：对每个频谱信号分为307个子模块，连接每个子模块的峰值点，获得包络线，以该包络线为新的数据集：2 880×307，将其输入诊断模型；方式 2：频域数据直接输入模型。图10为6种样本的频域曲线及相应的包络线，由图10可见，包络线可以很好的描述频域曲线的变化态势，不同类别样本之间的包络线区分明显。选取12.5%、25%、37.5%、50%、62.5%的样本用于训练SAE模型，全体数据集作为测试样本，对比方式1和方式2构建的诊断模型对测试样本的识别正确率、聚类效果Jb及F系数，验证所提方法的有效性。设置4种深度层数及相应的隐含层特征数分别为：空隐含层、单隐含层：80、双隐含层：80-50、三隐含层：80-50-20。为了实现低维聚类的可视化，设定高层输出维数为3。

图8 齿轮箱传动试验台、传感器布置及传递路线结构Fig.8 Transmission test-bed of gearbox, sensors arrangement and the structure of gearbox

图9 齿轮箱故障轴承及齿轮实物Fig.9 The fault bearing and gear

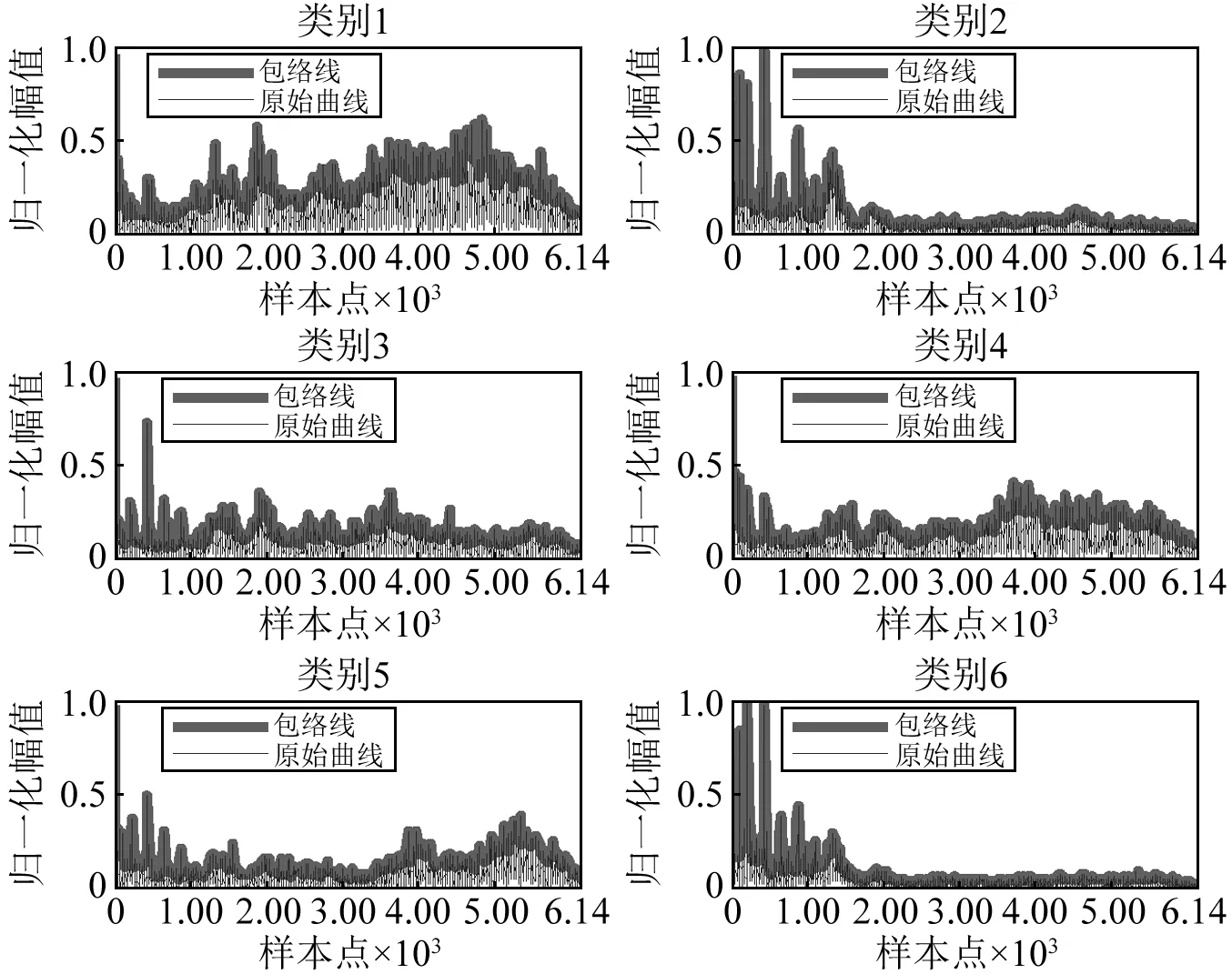
图10 6种类别样本的频域曲线及相应包络线Fig.10 The frequency domain curves and corresponding envelope of 6 classes

3.3 计算效率分析

表1为两种方式构建第一隐含层所需要的计算时间，由于方式1在第一隐含层所需要构建的权重矩阵为2×6 140×80，而方式2所需要构建的权重矩阵仅为2×307×80，两者相差20倍，因此计算效率也相差在12倍～20倍之间，而且由表可见，这种效果随着测试样本数的增加而区分越明显。

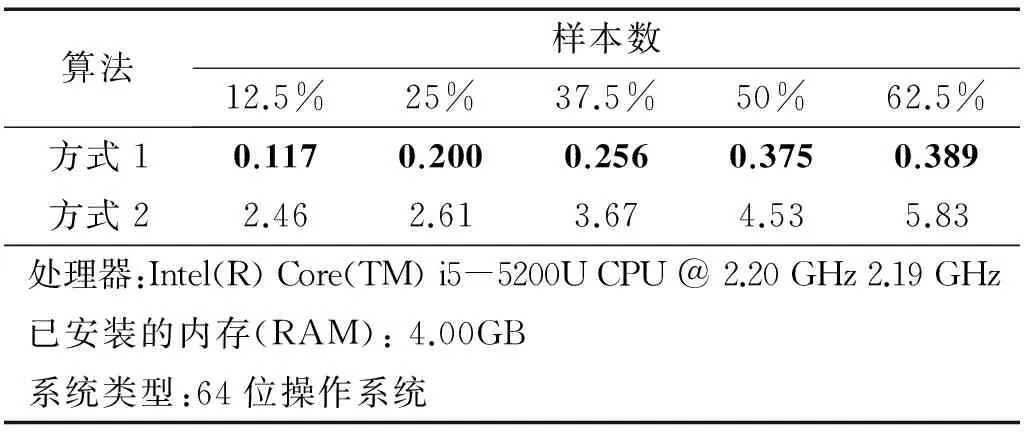
表1 两种数据处理方式所需计算时间

3.4 识别效果分析

对比图11的识别正确率曲线可见，包络特征的SAE诊断模型在5种训练样本数下得到的测试识别正确率均在94%以上，且在隐含层数大于0时，得到的测试识别正确率在99%以上(隐含层数为1和3，训练样本占比37.5%和50%，此时的识别正确率分别为：97.2%和98.2%)，取得较好的识别效果。而原始频域作为输入构建的SAE诊断模型在深度层数为0时，得到的识别正确率仅为16.7%，这是由于此时构建的是浅层SAE模型，无法很好的描述复杂频域成分。在深度层数大于0的情况下，原始频域构建的SAE诊断模型取得较好的识别正确率，但与方式1相差不大，表明方式1能够得到足够好的识别正确率。

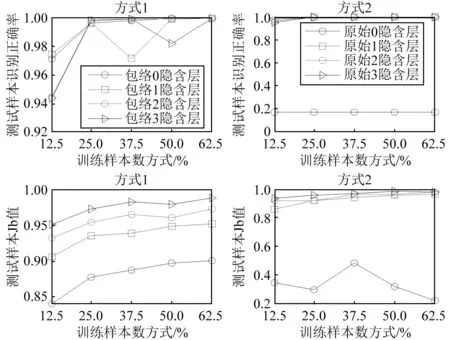
图11 两种方式的识别正确率及聚类效果Fig.11 Performance comparisons of two algorithms:case 1 and case 2

对比图11的聚类评价指标Jb值可见，方式1的聚类Jb值随着训练样本数的增加而增大，且随着深度层数的增加而增大，在隐含层数为0时，其Jb值在0.84～0.90之间，而在隐含层数大于0时，Jb值均在0.9以上，最优值为0.988 2，此时深度层数为3，训练样本数占比62.5%。方式2在隐含层数为0时，由于此时浅层结构的局限性，其Jb值在0.48以下，表明聚类效果较差，随深度层数增加，其聚类值亦增大，最优值为0.986 9，此时的深度层数为3，训练样本数占比50%。

对比图12的F系数指标可见，方式1在3种深度层数下的F系数值区间分别为：[0.905 7 0.95]、[0.940 2 0.976 4]、[0.938 6 0.986 4]和[0.947 8 0.994 1]，而方式2在3种深度层数下的F系数值区间分别为：[0.230 5 0.323 8]、[0.911 5 0.981 5]、[0.947 9 0.988 7]和[0.943 4 0.993 1]。在深度层数为0时的浅层结构下，方式1得到的F系数值远大于方式2，而当深度层数大于0时，方式1和方式2的F系数值相差不大，两者最大差值为2.87%和-1.65%(负号表示方式1小于方式2)。由此表明方式1构建的SAE诊断模型在浅层结构模型下能够获得比方式2更好的识别及聚类效果，而当构建的模型为深度结构时，得到的识别及聚类效果与方式2相当，在部分条件下优于方式2，而且此时方式1所需要的计算时间明显小于方式2，体现出频谱包络线处理降低计算复杂度的优点。

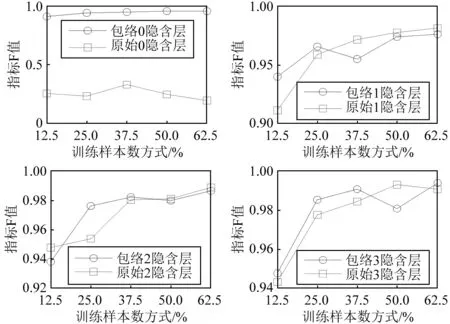
图12 不同深度层数下方式1和方式2的F系数Fig.12 Performance comparisons of two case under different deep levels

从上面的分析可见，随着隐含层数的增加，SAE诊断模型的聚类评价指标Jb和F系数增大。为了对比SAE诊断模型与浅层结构算法的识别及聚类效果，将包络处理后的数据集输入LPP及PCA算法中，此时SAE模型的隐含层数设置为0，即为SAE浅层结构模式，如果浅层SAE模型的识别及聚类效果优于PCA和LPP方法，则由上面的分析可知，深层SAE模型的识别及聚类效果亦优于浅层模式。识别正确率、聚类指标Jb及F系数指标分别如表2，表3及表4所示。

对比表2，表3，表4可见，由于原始数据包含的信息量较大，即输入数据的模式较为复杂，浅层SAE结构无法提取完整描述样本的状态信息，因此，此时算法的识别正确率、聚类效果及F系数均较差。经过包络处理后得到的数据集从一定程度上衰减干扰信息，强化样本的类别信息，因此，经过包络处理后的数据输入浅层SAE、PCA及LPP算法中能得到更好的效果。由于浅层SAE的权重参数经过后向微调过程的优化，因此，包络处理SAE方法得到的识别正确率(0.97以上)、聚类效果(0.84以上)及F系数(0.90以上)均明显大于其它算法，取得更好的识别及聚类效果。

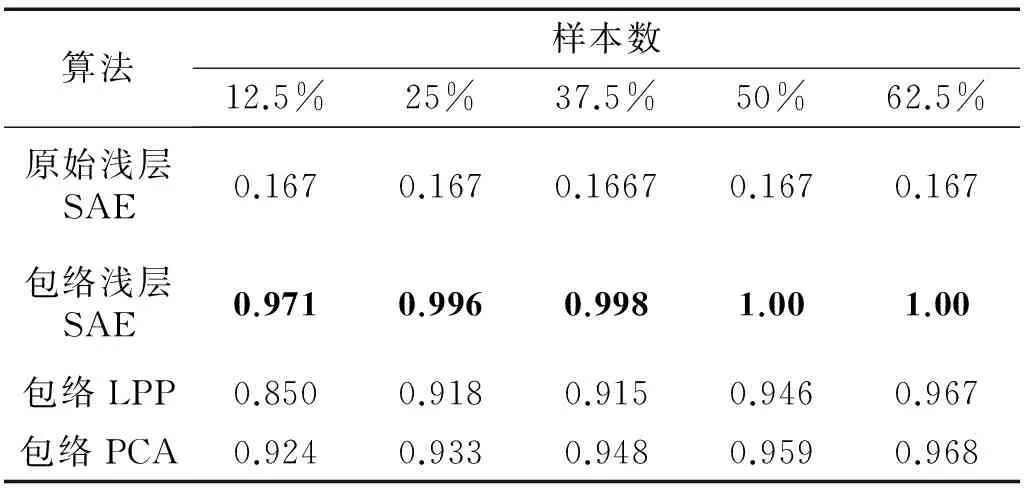
表2 浅层诊断模型的识别正确率

表3 浅层诊断模型的可分性指标jb

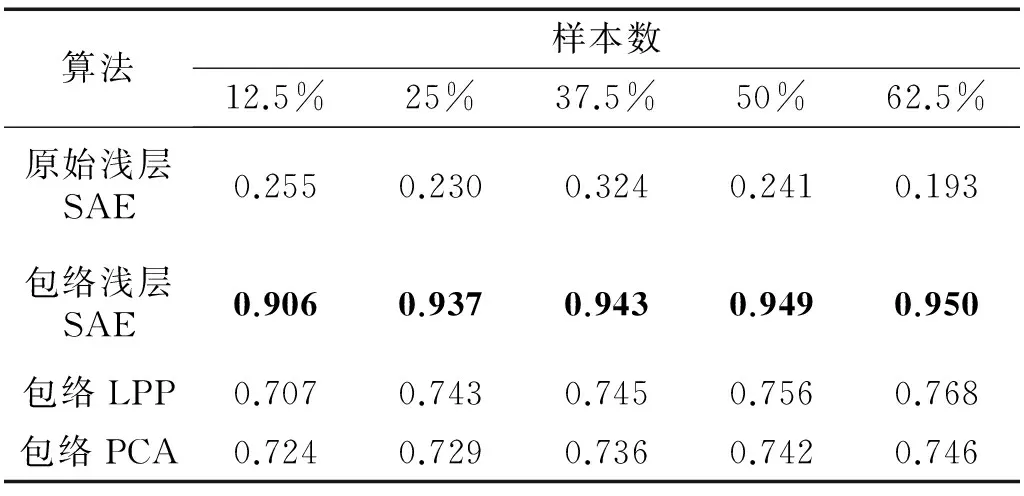
表4 浅层诊断模型的F系数

3.5 聚类效果分析

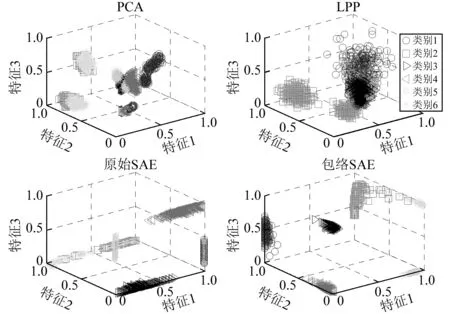
图13 4种方法的聚类效果三维图Fig.13 Clustering effect comparisons of different algorithms

图13 为在训练样本数占比为12.5%，所有样本作为测试样本下，4种方法的聚类效果三维图，其中SAE模型的深度层数为3，对比4个图可以看出，由于PCA、LPP均为浅层结构模型，所以聚类效果较差，同类样本分离明显，而异类样本之间存在严重混叠，除此之外，这两种算法依据工况的不同，出现同类样本的明显分离，无法消除工况信息，融合同类故障类型样本。由于原始SAE和包络SAE为深层结构模型，取得较好的聚类效果，可以消除工况信息的干扰，使得同类样本聚集，异类样本明显分离。对比原始SAE和包络SAE可见，原始SAE存在类别2、类别5和类别6的混叠，而包络SAE仅在类别2和类别6存在轻微混叠，且同类样本的聚集程度及异类样本的分离程度均明显优于原始SAE，取得更好的聚类效果。

3.6 包络块数分析

为了对比不同包络块数对识别效果的影响，对实验信号的频谱进行不同模块数的划分，对比在每个划分下的识别正确率，聚类指标Jb以及评价系数F值，具体效果如下图所示。

图14 不同包络块数的识别正确率Fig.14 The recognition accuracy of different envelope blocks

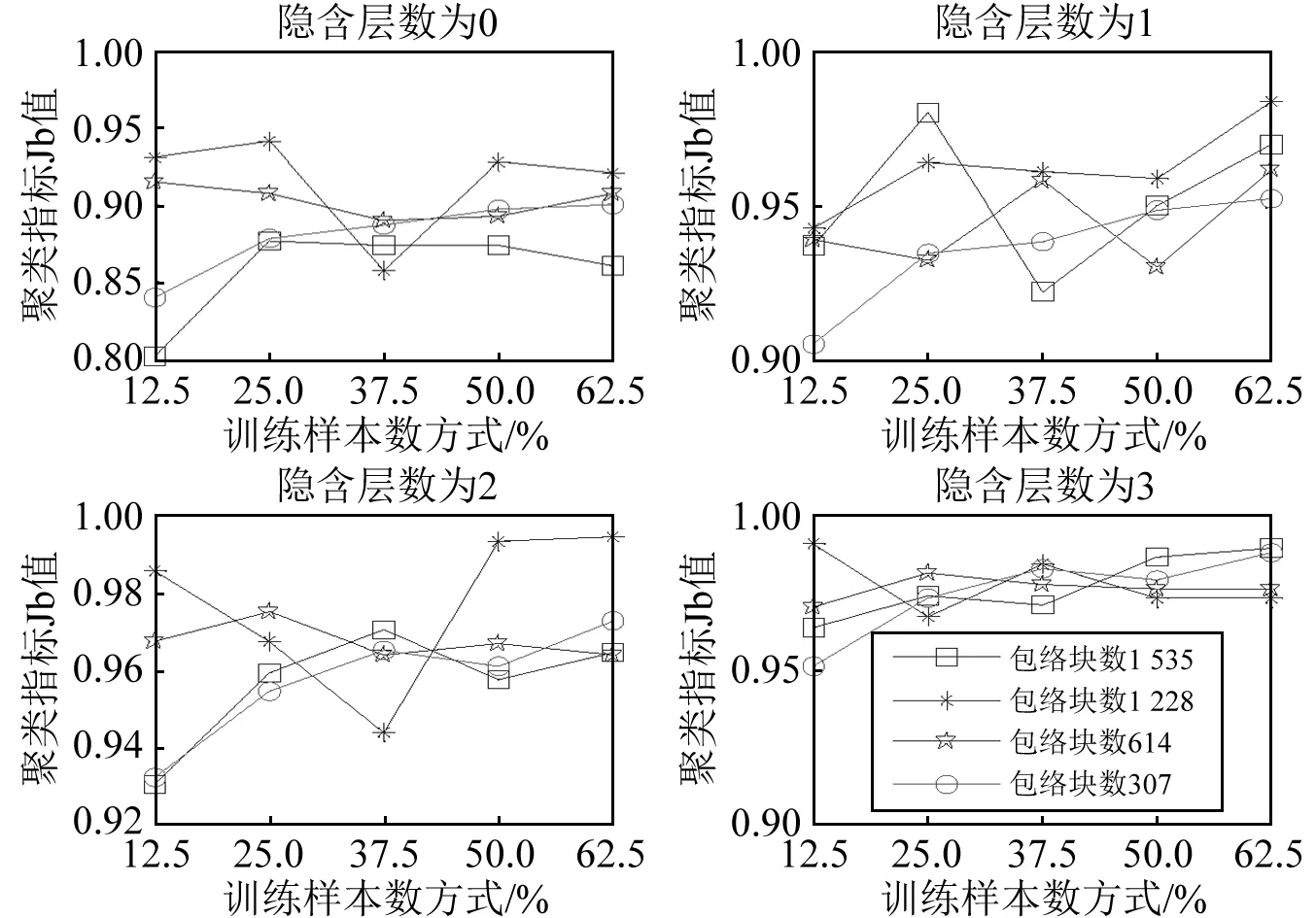
图15 不同包络块数的聚类指标Jb值Fig.15 The Jb value of different envelope blocks

图16 不同包络块数的综合评价指标F系数Fig.16 The F value of different envelope blocks

图14～16为实际测试信号在不同包络块数下的识别正确率、聚类指标Jb值及综合评价系数F值。从识别正确率曲线可见(图14)，包络块数为307时，得到的识别正确率较为稳定，其值在4种隐含层数及5种训练样本方式下均大于0.94，且此时的计算效率相比于原始6 140，第一隐含层的计算效率将提高20倍，从识别正确率及计算效率方面分析，该包络块数能取得更优的效果。

对比聚类评价指标Jb值可见(图15)，除隐含层数为0外，其余情况下不同包络块数得到的Jb值均在0.9以上，包络块数为614和1 228时，得到的识别正确率较为稳定，包络块数为307时得到的Jb值次之。由图16的综合评价指标F值可见，相比于其它包络块数，包络块数为307和1 228得到的F值在不同隐含层数及训练样本数下总体较好，两者的F值根据不同训练样本数及隐含层数各有优势，但选择包络块数为307得到的计算效率在第一隐含层处将提高20倍，而包络块数为1 228仅提高5倍。

4 结 论

(1)分析提高深度学习诊断模型识别效果的前期数据预处理方式，提出一种对采集到的时域信号经频域处理之后，再提取频域的包络线数据，在保证诊断模型识别效果的同时，降低算法的计算复杂度，提高诊断模型的适用性。

(2)通过仿真及6类齿轮箱状态样本数据，对比方式1(对频域数据提取包络线)和方式2(原始频域数据)的识别正确率、聚类效果、F系数及3维聚类效果，结果表明，深层结构能够取得较浅层结构更好的识别效果和聚类效果，在不同深度层数下，方式1能够在保证识别效果的同时，提高计算效率。

[ 1 ] 林近山, 陈前. 基于非平稳时间序列双标度指数特征的齿轮箱故障诊断[J]. 机械工程学报, 2012, 48(13): 108-114.

LIN Jinshan, CHEN Qian. Fault diagnosis of gearboxes based on the double-scaling-exponent characteristic of nonstationary time series[J]. Journal of Mechanical Engineering, 2012, 48(13): 108-114.

[ 2 ] 王健, 冯健, 韩志艳. 基于流形学习的局部保持PCA算法在故障检测中的应用[J]. 控制与决策,2013,28(5):683-687.

WANG Jian, FENG Jian, HAN Zhiyan. Locally preserving PCA method based on manifold learning and its application in fault detection[J].Control and Decision,2013,28(5):683-687.

[ 3 ] YU Jianbo. A nonlinear probabilistic method and contribution analysis for machine condition monitoring[J]. Mechanical Systems and Signal Processing, 2013(37): 293-314.

[ 4 ] HINTON G E, SALAKHUTDINOV R. Reducing the dimensionality of data with neural networks [J]. Science, 2006, 313: 504-507.

[ 5 ] HINTON G E, OSINDERO S,TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554.

[ 6 ] BENGIO Y. Learning deep architectures for AI[J]. Foundations and Trends in Machine Learning, 2009, 2(1):1-127.

[ 7 ] BENGIO Y, LAMBLIN P, POPOVICI D, et al. Greedy layer-wise training of deep networks[C]∥ Advances in Neural Information Processing Systems 19(NIPS’06), 2007, pages 153-160.

[ 8 ] 深度学习：推进人工智能的梦想[EB/OL].http://www.csdn.net/article/2013-05-29/2815479, 2013.

[ 9 ] Adam项目展示微软研究院人工智能领域新突破[EB/OL].http://blog.sina.com.cn/s/blog_4caedc7a0102uxma.html, 2014.

[10] TAMILSELVAN P, WANG P. Failure diagnosis using deep belief learning based health state classification[J]. Reliability Engineering and System Safety, 2013, 115: 124-135.

[11] TRAN V T, THOBIANI F A, BALL A. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaiser energy operator and deep belief networks[J]. Expert Systems with Applications, 2014, 41: 4113-4122.

[12] FU Yang, ZHANG Yun, QIAO Haiyu, et al. Analysis of feature extracting ability for cutting state monitoring using deep belief networks[J]. 15th CIRP Conference on Modelling of Machining Operations, 2015, 31: 29-34.

[13] HU Qinghua, ZHANG Rujia, ZHOU Yucan. Transfer learning for short-term wind speed prediction with deep neural networks[J]. Renewable Energy, 2016, 85: 83-95.

[14] GAN Meng, WANG Cong, ZHU Changan. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2016 (72/73): 92-104.

[15] 王宪保, 李洁, 姚明海, 等. 基于深度学习的太阳能电池片表面缺陷检测方法[J]. 模式识别与人工智能, 2014, 27(6): 517-523.

WANG Xianbao, LI Jie, YAO Minghai, et al. Solar cells surface defects detection based on deep learning[J]. Pattern Recognition and Artificial Intelligence, 2014, 27(6): 517-523.

[16] 黄海波, 李人宪, 杨琪, 等. 基于DBNs的车辆悬架减振器异响鉴别方法[J]. 西南交通大学学报, 2015, 50(5): 776-782.

HUANG Haibo, LI Renxian, YANG Qi, et al. Identifying abnormal noise of vehicle suspension shock absorber based on deep belief networks[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 776-782.

[17] 赵旻昊. 基于深度学习的数据融合在FPSO监测预警系统上的应用[D]. 天津：天津大学, 2013.

[18] 雷亚国, 贾峰, 周昕, 等. 基于深度学习理论的机械装备大数据健康监测方法[J]. 机械工程学报, 2015, 51(21): 49-56.

LEI Yaguo, JIA Feng, ZHOU Xin, et al. A Deep learning-based method for machinery health monitoring with big data[J]. Chinese Journal of Mechanical Engineering, 2015, 51(21): 49-56.

[19] 谢吉朋. 云平台下基于深度学习的高速列车走行部故障诊断技术研究[D]. 成都：西南交通大学, 2015.

[20] WANG Y F. KOOTSOOKOS P J. Modeling of low shaft speed bearing faults for condition monitoring[J]. Mechanical Systems and Signal Processing, 1998, 12(3): 415-426.

[21] 张绍辉, 李巍华. 可变近邻参数的局部线性嵌入算法及其在轴承状态识别中的应用[J]. 机械工程学报, 2013, 49(1): 81-87.

ZHANG Shaohui, LI Weihua. Variable nearest neighbor locally linear embedding and applications in bearing condition recognition [J]. Chinese Journal of Mechanical Engineering, 2013, 49(1): 81-87.