填筑层数对土石坝应力变形的影响研究

曾丽娇

（德兴市水利局，江西 上饶 334200）

0 引言

合理地获取土石坝施工过程中的应力变形至关重要。随着数值模拟技术日趋成熟，采用数值模拟方法已成为计算填筑体竣工期应力变形的重要手段。对于土石坝而言，通常是分层填筑，数值模拟结果随计算分析师人为控制的分层层数所控制。因此，在土石坝的应力变形分析计算中，合理地选择模拟填筑层数是十分必要的。

前人研究成果：唐岷等[1]对300 m 级高土石坝进行应力应变分析，建议模拟层数达到25～30 层。江德军等[2]对100 m 级土石坝进行了不同填筑层数的施工过程模拟，以探究不同填筑层数对大坝最终位移场的影响，结果表明，当模拟过程中分层过粗时会导致结果失真，当分层数达10 层左右时，可满足计算精度要求。周爱红等[3]对模拟填筑层数进行了研究，结果表明，相对坝体沉降来说，水平位移和稳定系数对填筑层数的敏感性较小，并提出了坝体分层从坝底到坝顶分3个区域，按疏-中-密的原则选择填筑层数。然而，前人通常是针对特定坝高，采用不同填筑层数进行模拟，得到的结果并不一定适用于其他高度的大坝。因为不同高度的土石坝，最适宜的填筑层数可能不一致；虽然说，工程中每层填筑厚度是在一定范围之内，但是在数值模拟中，尤其是针对百米级坝高，若按照实际施工过程中的填筑厚度进行分层填筑模拟，则严重影响计算效率。

鉴于此，本文考虑30 m 级均质坝、70 m 级均质坝、100 m 级均质坝及100 m 级沥青混凝土心墙坝，采用有限元软件MADIS GTS NX 计算坝体的应力变形，分析分层层数对土石坝应力变形的影响，研究结果可为土石坝填筑模拟提供一定参考依据。

1 有限元模型建立及计算方案

1.1 计算模型及方案

分别以30，70，100 m均质坝和100 m心墙坝为研究对象，上游坡比取1∶2.5，下游坡比取1∶2.2，建立土石坝二维模型，其模型简图见图1，其中H代表坝高。

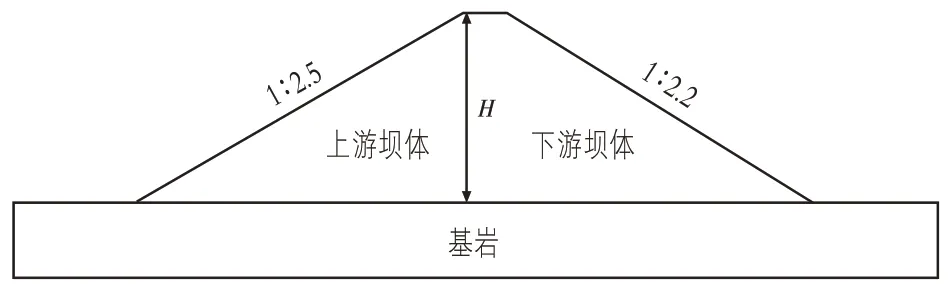
图1 土石坝模型简图

填筑体采用分层填筑，分别进行了1 层、4 层、8 层、16 层和32 层（共20 种工况）的模拟计算，在此基础上研究填筑层数对模型最终变形量的影响，具体计算方案见表1。

表1 计算方案表

1.2 材料参数取值

采用MADIS GTS NX 岩土工程软件中的E-B模型对上述算例进行施工过程的模拟计算，大坝、心墙及过渡层的各层材料E-B材料参数见表2。

表2 坝体材料物理学指标

鉴于基岩、基座和帷幕的变形较小，故对其采用线弹性模型。其中基岩的弹性模量为30 GPa，泊松比为0.20；基座的弹性模量为30 GPa，泊松比为0.167；帷幕的弹性模量为30 GPa，泊松比为0.200。此外，均质坝的坝体和基岩材料参数取值同心墙坝，心墙坝与均质坝的上下游坝体材料参数取值均为同一参数。

1.3 边界条件

为模拟大坝施工过程，假定坝料填筑重力荷载为一次性施加，施工前认为坝基已经沉降完成，以坝基自重产生的天然应力作为初始应力场，坝基上下游设置为无限区域并施加水平约束，坝基底面各方向均为完全约束，即坝基只能发生竖向沉降，坝体部分均不设置约束[4]。

2 计算结果及分析

2.1 填筑层数对坝体变形趋势的影响

由于计算工况较多，每组工况计算结果云图较为相似，因此，本文仅给出工况4-1，4-2，4-3，4-4 和4-5 的竖向变形云图（横向变形云图的变化相对较小，限于文章篇幅，此处不再列举），见图2。结果中，变形以竖直向上为正，向下为负。

由图2可以看出，当填筑层数为1时，坝体最大变形位置出现在坝顶处，竖向变形云图等值线光滑连续；当填筑层数为4时，竖向变形云图的层间界限变得非常明显，由于填筑层的厚度较厚，每一填筑层都出现一个相对最大的竖向变形晕圈，各层晕圈之间连续性极差，最大竖向变形位置出现在坝顶偏下处；当填筑层数为8时，竖向变形云图的层间界限依旧明显，各层晕圈逐渐融合成为一个整体，云图等值线连续性较差，最大竖向变形位置出现在坝体中部偏上处；当填筑层数达到16 时，各层晕圈融合成为一个整体，竖向变形云图等值线呈锯齿状，最大竖向变形位置出现在坝体中部处；当填筑层数为32 时，云图等值线为光滑的连续曲线，变形量最大的位置出现在坝体中部约1/2坝高处。

图2 100 m 心墙坝分层填筑竖向变形云图

2.2 填筑层数对坝体最大变形的影响

2.2.1 最大水平变形

选取不同高度的均质坝及沥青混凝土心墙坝进行有限元建模分析，计算得到坝体施工期最大水平位移值，见表3。为分析坝体水平变形量随填筑层数的变化规律，根据计算中各监控点水平最大正（负）位移值绘制水平最大正（负）位移变化对填筑层数的变化曲线，见图3、图4。

表3 大坝不同填筑层数与水平位移统计表

如图3、图4 所示，随着填筑层数N的增加，不同坝高的土石坝最大水平位移逐渐增大，当N到达一定值时，最大水平位移趋于平稳。当坝高为30 m时，坝体水平位移受填筑层数的影响较小，其水平最大正（负）位移变化对填筑层数的变化曲线近乎一条平行于横轴的直线；当坝高为70 m 和100 m时，N在4 时土石坝最大水平位移值趋于不变；填筑层数对100 m 坝高的沥青混凝土心墙坝与均质坝的最大水平正（负）位移影响比较相似。

图3 大坝水平最大正位移图

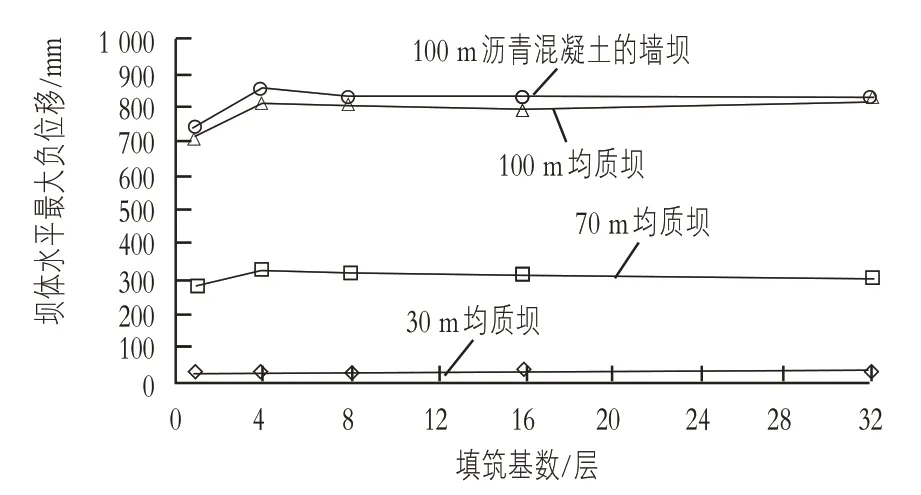
图4 大坝水平最大负位移图

2.2.2 最大竖向变形

选取不同高度的均质坝及沥青混凝土心墙坝进行有限元建模分析，计算得到坝体施工期最大竖向沉降值，见表4。为分析坝体竖向变形量随填筑层数的变化规律，根据计算中各监控点沉降位移值绘制沉降位移变化对填筑层数的变化曲线，见图5。

表4 大坝不同填筑层数与最大竖向

如图5 所示，随着填筑层数N的增加，不同坝高的土石坝最大沉降变形逐渐减小，当N到达一定值时，最大沉降趋于平稳。当坝高为30 m时，N在4时土石坝最大沉降即趋于不变；当坝高为70 m 和100 m 时，N在8 时土石坝最大沉降即趋于不变；其中，填筑层数对100 m 坝高的心墙坝和均质坝的最大竖向变形量的影响非常相似，两者的沉降位移变化对填筑层数的变化曲线几乎重合。

图5 大坝最大竖向变形图

2.3 填筑层数对坝体应力的影响

由于均质坝与沥青混凝土心墙坝内部结构有所不同，其应力差别较大，可比性较小，故本文只对3 种坝高的均质坝进行应力分析计算，计算得到坝体施工期最大竖向应力及最大水平应力值，见表5。为分析坝体最大应力随填筑层数变化规律，根据计算中各监控点绘制最大应力变化对填筑层数的变化曲线，见图6、图7。

表5 不同填筑层数与坝体最大应力统计表 kPa

根据上述表格和图6、图7 可以看出：坝体最大竖向应力和最大水平应力对填筑层数的敏感性均较小，随着填筑层数的增加，最大竖向、水平应力对填筑层数的变化曲线近似水平；相同填筑层数下，最大竖向、水平应力随着坝高的增大而增大。

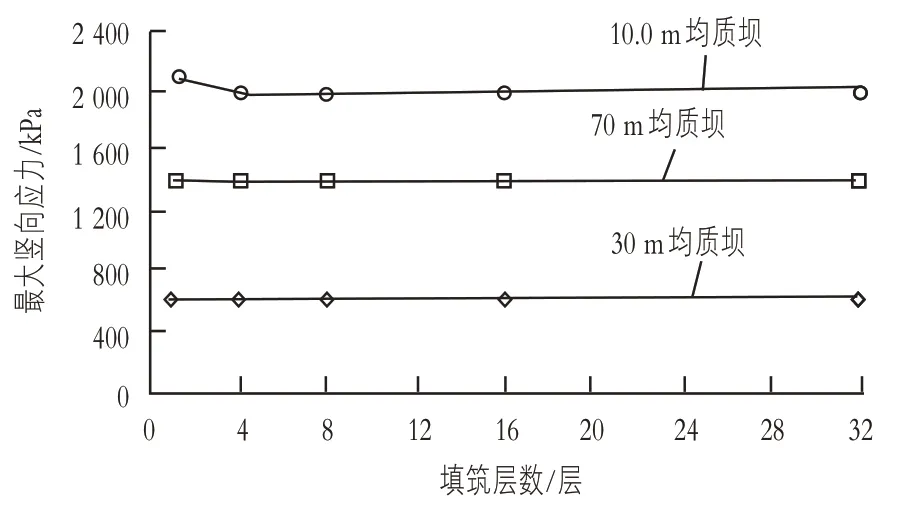
图6 最大竖向应力随填筑层数变化图

图7 最大水平应力随填筑层数变化图

3 结论

通过模拟土石坝分层填筑下，不同填筑层数对坝体竖向与水平变形的影响，得出以下结论：

1）填筑层数对坝体变化趋势和沉降云图的光滑连续性具有一定影响。当填筑层数较少时，模拟得到的沉降云图会呈现出层与层之间的相对独立性，且相对最大沉降量出现在各层中部偏上的位置，随着填筑层数的增加，这种层间相对独立性逐渐消失，呈现出各相对最大沉降晕圈逐渐融合，沉降云图等值线整体上逐渐光滑，愈加接近真实情况。

2）填筑层数与坝体最大沉降的关系，总体趋势是坝体最大沉降量随着填筑层数的增加呈非线性递减，在填筑层数达到一定层数以后，最大沉降量随填筑层数的变化趋于稳定。对于30 m 级的均质土石坝，在进行沉降量数值模拟计算时，建议其填筑层数至少达到8～16 层；对于70 m 级的均质土石坝、100 m 级的均质土石坝和100 m 级的沥青混凝土心墙土石坝在进行沉降量数值模拟计算时，建议其填筑层数至少达到16～32 层。模拟填筑层数对坝体水平位移影响较小，对不同坝高的土石坝，当模拟填筑层数达到4 层时，其水平位移随填筑层数的变化趋于稳定。

3）坝体最大竖向、水平应力值随坝高的增大而增大，但几乎不受填筑层数的影响。数值模拟中，相同坝高的均质土石坝和沥青混凝土心墙坝受填筑层数的影响差别较小，两者计算结果非常相近。