利用提示语培养学生提出问题的策略

南京航空航天大学附属高级中学 晋 杰 孔德鹏

一、问题

爱因斯坦说：“提出一个问题往往比解决一个问题更为重要，因为解决一个问题也许只是一个数学上或实验上的技巧问题。而提出新的问题、新的可能性，从新的角度看旧问题，却需要创造性的想象力，而且标志着科学的真正进步。”可见，培养学生提出问题的能力是教师开展教学实现育人价值的追求。新课程标准在“四基”上发展“四能”——发现和提出问题的能力、分析和解决问题的能力，首要的更是发现和提出问题的能力培养。“现实教学中特别是在高考主导的学习模式下，学生学习的方式方法略显单一，还有被动学习、疯狂刷题、频繁考试强刺激练习现象存在，这样导致学生缺乏自主学主动学，对提升学生的核心素养极为不利”。可见，也不利于学生提出问题的意识或者上升能力的培养。不能提出问题实质就是缺乏想象力。

数学是思维的体操，思维的发生首先要发现问题、提出问题。基于学生学习的现实，提出问题的教学必应引起教师的重视。通过培养学生提出问题帮助学生获取思考的方式、研究问题的一般方法，也是对培养学生的问题意识、好奇心理和数学关键能力具有积极意义。

二、突破

看重学生提出问题的教学，教师要善于运用“启发性提示语”，这是南师大涂荣豹教授提出的提问策略，实质就是启发思维。启发思维要基于平等的师生关系，课堂上营造开放、活泼、民主的氛围，鼓励学生大胆设想、踊跃发言，积极激励学生。古语有云：“学贵有疑，小疑则小进，大疑则大进。”鼓励学生质疑、提出问题的过程在方法上要有一些教学策略。

1．利用元认知提示语启发引导

元认知就是个人对于自己认知活动的认知，包括三个方面：元认知知识、元认知体验、元认知监控，其实质是人对认识或认知活动的自我意识和自我控制。“元认知提示语”是涂教授提出的一种教学启发方法[2]，是教师对学生元认知活动的提问与监控，目的是“激发学生的自我意识，关注自身认知活动的进程，促使其选择认知活动的策略，分析当前遇到的困难并决定是否作出调整以及如何调整”。启发性提示语“从用隐蔽性强的弱暗示提示语进行启发，到用隐蔽性逐步减弱的强暗示提示语进行启发，用这样的‘分级提问’来达到对不同层次学生的引导”。在教师引导下，学生的认知逐渐趋于清晰、规范、准确，有利于学生提出问题、解决问题能力的发展。

【教学案例一】双曲线的几何性质

学生能够提出有价值的问题，离不开教师的启发。在学习了椭圆的概念、方程与几何性质基础上，引导学生回顾反思、提出问题，构建“前后一致、逻辑连贯”的数学系统，教学中可以这样启发学生：

我们当前学习了什么内容？——双曲线的定义；

你想进一步研究什么问题？——类比椭圆，提出要研究双曲线的几何性质问题；

你打算怎样研究呢？——遇到新问题，就要回顾联想旧问题的解决方法，寻找借鉴之法；

我们是怎样研究椭圆的几何性质的？——用椭圆的方程；

对我们这个问题有借鉴意义吗？——学生要尝试、思考，否定；

方程的本质是什么？——代数方法，解析几何的本质；

获得双曲线的几何性质从哪里入手？——回到双曲线的方程与定义上；

那么，怎样得到性质呢？——学生观察方程结构，从特殊到一般归纳、说理；类比椭圆的几何性质：范围、定点、焦点、准线、离心率，引导学生探究。

通过教师的启发，引导学生思考。通过双曲线几何性质的学习让学生经历提出问题、解决问题的过程，是培养学生数学核心素养的必要手段。在此过程中，通过元认知提示语的强化与运用，帮助学生的思维走向深入，由表及里，获得有意义思考的经验。

2．看重提升分析能力，学会自我提问

波利亚在著作《怎样解题》中讨论了发现和发明的一般方法与规律，对进行怎样思维如何思考具有明显的指导意义，归纳出著名的“解题表”——弄清题意、拟定计划、实施计划、回顾反思。解题的过程就是不断探索的过程，就是分析转化的过程，这其中伴随着自我提问。自我提问也是利用元认知提示语。解决问题的关键是理解题意，理解题意的过程就是分析问题的过程。而在实际教学中，学生对题目的理解上存在着严重的问题。这就需要教师教给学生理解题意的方法，学习自我提问之术，发展提出问题的能力。

【教学案例二】习题教学

已知△ABC三个内角A，B，C的对应边分别为a，b，c，且C当取得最大值时，求的值。

学生的“心路历程”：

这是一个什么问题？——解三角形，向量数量积；

解三角形有哪些工具可以用？——正弦定理或余弦定理。

视角二：利用余弦定理，4=a2+b2-ab，

这样就把原来的问题转为“4=a2+b2-ab，a，b＞0，求b2-a2的最大值”。

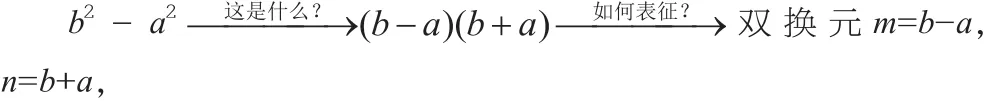
转化为：3m2+n2=16，求mn的最大值。

波利亚有言：“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找找，很可能附近就有好几个。”要培养学生开阔的数学视野，从不同视角分析问题、解决问题的能力，就要引导学生自主思考、自发提问。

数学的育人功能不只是体现在“传道解惑”——教给学生基本知识基本技能，更应该体现在培养学生的思维能力——思考的习惯、思考的方法——发现问题、提出问题、分析问题、解决问题的能力。教学中不只要顾及眼前的“苟且”——抓成绩，更要胸怀“诗与远方”——立德树人，发展人的潜能。提出问题应是一个良师关注的教学问题，并在教学中勇于尝试，不断发展，站在学生长远利益的高度理解学生、理解数学、理解教学。