浅析高中数学解题的思维策略

江苏省启东市吕四中学 朱晓燕

数学问题解决的思维策略是发现和应用数学知识的方法。在解决数学问题的过程中采用的思想，它将从未知变为简单，从而快速准确地解决问题。用解题的思维策略去启发学生“不要只埋头走路，还要抬头看路”，下面作者讨论了解决实际问题的一些经验。

一、认真审题，紧扣概念，快速分辨

解决数学问题的第一步是检验问题。弄清已知条件的等价说法，实施相应的问题解决策略。数学中的定理、公式、性质和定律都来自定义和公式。定义是一种逻辑方法，揭示了概念的内涵。在解决问题时，我们应该首先回到概念和定义，看看我们是否可以通过概念或定义来解决问题。

例1 已知点P（x，y）满足方程x+y-1 =0，求点P（x，y）的轨迹。

问题解决策略分析：简化等式。用xy项对二元二次方程的相应曲线进行讨论，只需要判断曲线的形状，并选择圆形、抛物线、椭圆和双曲线中的一种，并回到四者的概念或定义，然后问题得到解决。

分析将原始方程变形为x+y=1，即y=x-1，因为它表示原点O（0，0）到点P（x，y）的距离，以及从点P（x，y）到直线x+y-1=0的距离，因此该等式的几何意义是移动点P（x，y）从固定点O（0，0）到固定直线x+y-1=0的距离是1，所以P点的轨迹是双曲线。

解决后的思考1：曲线和方程是“形式”和“数字”的具体表现形式。找到曲线方程，用已知方程来研究曲线。

思考2：椭圆、双曲线和抛物线是解析几何中的主要内容。在解决具体问题时，尽可能回到定义和概念，以便出现意外的惊喜和解决问题的经验。

二、找准题眼，把握特色，明确思路

数学问题不断变化。善于根据相关专业知识制定灵活的想法和解决问题的解决方案。教师必须注意观察能力的培养，使学生不仅可以用常规方式解决问题，还可以根据课题的具体特点，使用特殊方法解决问题，从而达到正确解决问题的目的。

例2 已知a，b，c，d都是实数，求证：

问题解决策略分析：证明不平等的三种最常见的方法是比较方法、综合方法和分析方法。结论的右端与平面上的两个点之间的距离的公式非常相似，左端可以被视为从点到原点的距离公式。

这个问题可用于以下聪明和简单的证明。证明：不妨设A（a，b），B（c，d），如图1所示，则在△OAB中，由三角形三边之间的关系知OA+OB≥AB，当且仅当O在AB上时，等号成立，因此

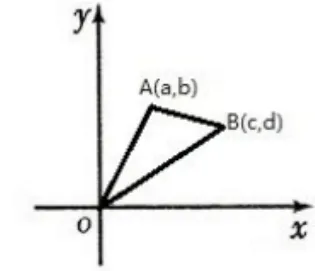
图1

在解决方案之后重新思考在证明这种不平等的过程中，我们对问题的解决方案通常是使用一些基本方法来证明不平等。我立刻想到了使用分析方法，综合方法等。使用这些方法这个问题非常麻烦，它不熟悉这个公式，而且进一步说，对基础知识的掌握并不牢固。

三、联想方法，思考纠正，总结反思

著名的荷兰数学家弗赖登塔尔曾指出过这一点：“反思是数学思维活动的核心和动力”“通过反思才能使现实世界数学化”。著名的数学家波利亚也说过“如果没有反思，他们将错过理解问题的重要而有效的方面”。通过反思，我们可以加深对问题的理解，优化思维过程，揭示问题的本质，探索一般规律；通过反思，我们可以传达知识之间的相互关系，从而促进知识的同化和迁移，并产生新的发现。

它通常只是一个解决任务的问题，在你完成之后抛出一个问题，或者立即做另一个问题，仅限于解决问题的基本水平。每次我们提出问题时，都要注意思考和总结。特别是，如果你已经完成了问题，你应该掌握解决问题的方法，并将其与你当时的想法进行比较，查看你自己的想法或想法的问题，然后再做一次，看看是否有更好的想法和解决问题的方法，实现多种解题方法的贯通。

例3 已知a，b，c，d均为正数，求证：（ab+cd）·（ac+bd）≥4abcd。

问题解决策略分析：这个问题很容易让学生使用基本的不平等证明，但在评论之后，我们引导学生观察和反思，并发现问题的本质是“几何平均值不大于算术平均值”。

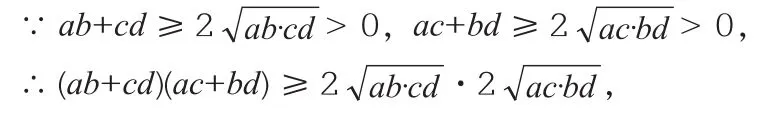
即（ab+cd）·（ac+bd）≥4abcd。

解决方案后的反思指导学生反思可以通过以下方面来完成：（1）思考过程的得失。这些障碍是怎样克服的？在解题策略上有何启示？（2）思维问题解决模式。如果标题的条件和结论得到适当改变，问题将如何改变？有什么规律？解决这个问题是否还有更佳的方法？对于典型问题，学习分析问题并掌握一类问题。以不同的方式，提高解决问题的能力。灵活运用一些数学思维方法，这是一个战略层面，在解决具体问题方面具有指导作用。不要用特定的方法来解决问题，还要运用相应的数学思想来统一思想，引导思维。

“知识”是基础，“方法”是手段，“思想”是本质。在不断学习和反复使用知识、方法和思想的过程中，提取了理解数学和解决问题的基本思想。学生必须练习，自我探索和合作，并获得特定问题解决活动的经验。提炼想法，形成自己的方法。