着眼学科素养的小学数学复习课范式探究——以“圆柱的体积”知识复习为例

江苏省南通市通州区英雄小学 徐红兵

在实际教学中，我们不仅要关注基础知识与基本技能的教学，而且更要关注数学的基本思想和基本活动经验。我们在教学中理应顺应时代潮流，着眼学科素养提升。下面以苏教版六年级下册“圆柱的体积”知识复习为例谈谈如何上好复习课。

一、抓住常规、破除定势

“能够运用体积公式准确求出圆柱的体积”是我们的教学目标之一。那么要求圆柱的体积，要知道什么条件呢？复习时可以按照这样的几个层次练习：（单位不统一，需要换算的除外）

基础层次 S底、h 直接运用公式巩固层次 r、h或者d、h 先求S底，再运用公式提升层次1 C底、h 先求r，再求S底，再运用公式提升层次2 S侧、h 先求C底，再求r，再求S底，再运用公式

上面四个层次中，h这个条件始终不变，体现了一个延续性，学生通过这样的复习可以很好地掌握圆柱的体积公式。

以上的复习可以看作变式了的常规回顾，学生只要环环相扣，基本上能解决，难度也不大。但是，总是重复训练，学生容易产生厌烦情绪和思维定式，因此需要求变。比如我在复习课上出示了这样一道题：

圆柱的侧面积是25.12平方厘米，底面半径是2厘米，圆柱的体积是多少平方厘米？

这一道题乍一看比较难，因为在一般学生的眼中，要计算圆柱的体积，还缺少圆柱的高，于是绞尽脑汁这样解答：先由侧面积逆推出高：25.12÷（2×2×3.14）=2（厘米）；再利用圆柱体积公式计算出体积：2×2×3.14×2=25.12（立方厘米）。其实，这一道题可以这样来解答：25.12÷2×2=25.12（立方厘米）。理由是将切拼好的长方体躺过来放：

这里我们可以看出，我们的学生太习惯于解决基本图形，思维定势，比如脑海里的线段一般是水平方向的，直角三角形的直角一般不会在上面等等。由此可见，培养学生的空间观念，提升学生的学科素养需要大量的实践活动，学生要有大量的时间和机会去观察、去操作，从而对事物产生直觉感知。有了上一题的经验，学生就能解释下面这个问题：

将一张长方形的纸卷成圆柱形的纸筒，接头处不计，怎样卷空间最大？

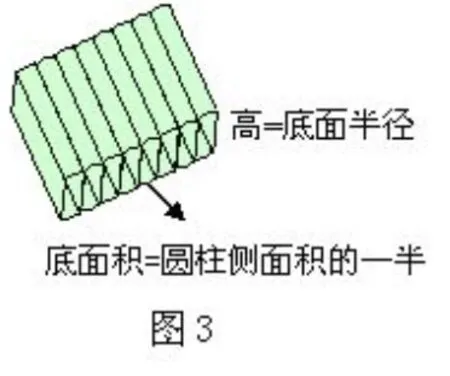
答案显而易见，把纸的长边作为底面周长，卷成的圆柱纸筒空间大，因为“体积＝侧面积÷2×半径”，卷法虽不同，但侧面积不变，所以底面周长大的空间大。

二、重视思想、感悟方法

苏教版“圆柱的体积”这一内容，教材是这样安排的：

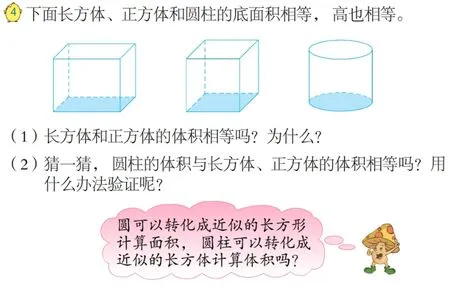
教材旨在考虑学生现实的认知水平，激发已有的知识和经验，让学生在比较底面积相等高也相等的长方体、正方体和圆柱体积之间关系的过程中，初步建立有关圆柱体积计算方法的猜想，启发学生利用以前学习探索圆的面积公式的方法验证建立的猜想。要让学生体验到数学家们在遇到新问题时，往往想方设法与已知问题建立某种联系。在随后的练习中有这样一道题：

学生在计算“大棚内空间有多大”时，大多数用“圆柱的体积÷2”来解决，这本无可厚非。然而回顾圆柱体积公式的推导过程，我们是不是真正把“转化”思想落到实处。联系到图形面积的转化，在复习课上我补充了以下内容：

经过这样的学习探索，学生在解决第14题时，自觉运用柱体体积计算公式“底面积×高”，也就是“半圆面积×大棚长”，这样既丰盈了转化的数学思想，又拓展了知识的深度。

三、善于沟通、形成网络

数学是一门逻辑性很强、前后知识联系很紧密的学科，我们在教学中要善于把握新旧知识的联系，让学生在已有的知识基础上学习新知。因此，我们在复习时要注重进行综合练习，例如：

为了更好地解决其中第二个问题，我们需要把推导体积公式的模型拿出来，让学生比较一下，切拼之后什么变化了，什么没有变。

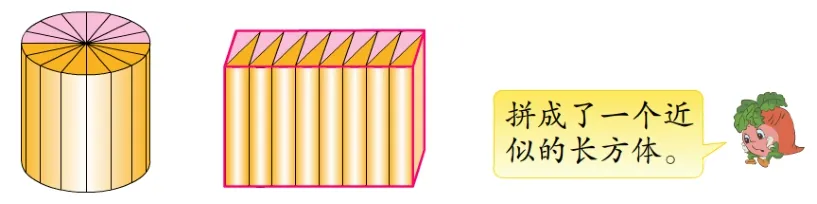
使学生在操作中意识到体积不变，表面积增加2个长方形，可以用“2×rh”来计算。

此外，我们要意识到现实世界是丰富多彩的，为避免形成强烈反差，因此培养学生空间观念不能仅仅停留在静态的层面，要适当融合关于位置、方向、运动、变化的元素，以达到更好的效果。如：

四、有效拓展、促进提升

在复习课上适当补充数学故事、数学名题等不仅能激发兴趣，更主要从另一个角度深化对知识的理解，比如：

要理解古人的算法，就是学生对圆柱体积公式以及运算性质的一次检验。在复习“圆柱的体积”时，要多给学生一点时间和空间，转移教学重心，从只关注计算体积变革为关注观念、能力、计算并重，适度拓展学习的内容，以“活动”贯穿学习始终，让“表象”存于学生头脑，“体验”积累于学生心中，更好地发展学生空间观念。

总之，无论复习课采用何种教学方式，都要认真把握复习课的功能，充分发挥学生的主体地位，让学生积极主动参与复习的全过程，重点关注三维目标的达成，促进学生素质的提升。