例谈插空法解不相邻问题
2018-02-14赵碧波
赵碧波
【摘要】 排列组合问题是高考的热点,也是高中数学教学的难点.本文针对插空法解决排列组合中的不相邻问题进行了深入而细致的研究.让学生体会数学核心概念,数学思想方法,特殊技巧是相辅相成的,才能从本质上理解“插空法”.
【关键词】 插空法;树形图;数学本质
不相邻问题是排列组合中常见的一种题型.但常见的问题,不见得就简单.下面,通过具体的例题,体会从数学本质上把握插空法精髓的重要性.
例1 电影院某排有7个座位连成一排,3人就座,若3人顺序一定,且互不相邻,则不同的坐法共有______种.
分析 这个具体的生活场景,学生(包括初学者)还是很好理解的.把7个座位,理解成7个相同的元素.由插空法可知:3人就座,需要占用3个座位,因此,还剩下4个座位形成5个空位,再将3个座位放入5个空位中的任意3个空位上,人再按序入座,即可.由于3人顺序一定,由计数原理共有N=C3 5·1=10种.
下面看,一个类似地,但相对抽象的不相邻问题:
例2 从1,2,3,…,20这20个正整数中,取出3个互不相邻的正整数,共有多少种不同的取法?
分析 这是一个不相邻问题,但不少学生不知所措.因为他们对“不相邻问题,插空法”这句话的理解存在偏差.常停留在这句话的表面,认为“放入”不相邻元素是插空法,而没有利用“一一对应”的思维模式,“取出”不相邻的元素,其实也是一种典型的插空法.为了使学生能够形象地理解这个比较抽象的问题.我们可以类比创造出形如例题1的具体情境.例如,将“1~20这20个正整数”理解成“电影院某排有20个座位连成一排”,“取出3个互不相邻的元素”理解成“有3人按序且互不相邻入座”,这种“一一对应”的想法,对问题进行了合理的转化,就豁然开朗.因此,剩下的17个座位就有18个空位,选择3个空位放入3个元素即可.因此,共有N=C3 18 =816种.
例3 集合A={1,2,3,…,2018}的12元子集B={a 1,a 2,…,a 12 }中,任取两个元素的差的绝对值不为1,这样的12元子集B的个数为多少(用公式表达)?
分析 “任取两个元素的差的绝对值不为1”等价于“任意两个元素互不相邻”,问题就转化成例题2的模式:从1,2,…,2018这2018个正整数中,取出12个互不相邻的正整数,共有多少种不同的取法?
因此,共有N=C 12 2018-12+1 =C 12 2007 种.
例4 某次文艺汇演中有5个指定节目,其中歌曲2个,小品2个,舞蹈1个,规定表演时同一类型的节目都不连续演出,则这5个节目演出顺序共有______种.
这是一道相邻与不相邻问题的综合题,属于中档题.许多中等偏下的学生,考虑不全,甚至无处下手.殊不知,画树形图也是解决排列组合最基本、最有效的方法之一(但不少同学认为这种方法不入眼,觉得是一种笨方法).可事实并非如此.曾记否,以前文科的学生,解決排列组合的问题都是“画”出来的.
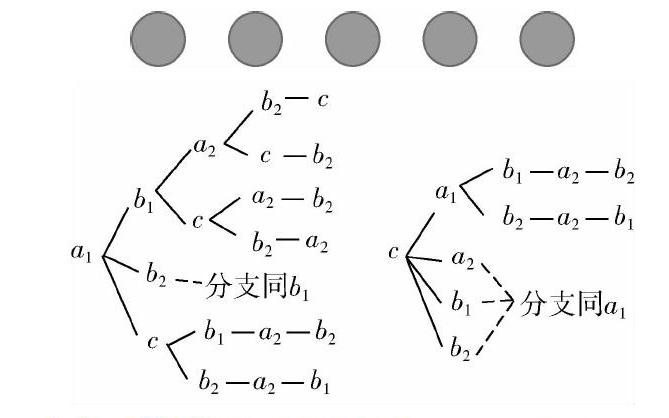
画树形图前(追求简洁性),我们首先要进行数学抽象:分别把2个歌曲,2个小品,1个舞蹈用数学符号语言表达,如分别用a 1,a 2;b 1,b 2;c表示.再放手让学生去画,发现不少学生“画”出了正确结果.但花的时间比较长,究其原因,本质上,学生还是没有掌握“画”的技巧.不少学生画的面面俱到,有的甚至画错.有如下5个位置,我们按照要求把5个节目“画”好就行.
第一个位置的节目可以“画”:a 1,a 2,b 1,b 2,c,这5个元素中的任意一个,但我们仔细分析发现放入a 1,a 2,b 1,b 2,中的每一个元素,后面画的分支的总数,从数量上看是完全一样的.因此,我们只需画出a 1与c开始的树形图即可.
如图1所示,有(4×2+2)×4+4×2=48种.
方法2 直接法.
当2个歌曲不相邻时(此时,2个小品可以相邻也可以不相邻),有A3 3·A2 4=72种,而歌曲和小品都相邻时,有 A2 2· A2 2·A2 3=24.因此,符合条件的有N=72-24=48种.
方法3 间接法.
“正难或正繁,则反”.用间接法处理,5个节目的全排列,减去歌曲、小品都相邻的时候和歌曲、小品只有一类相邻,另一类不相邻的时候.则符合条件的有N=A5 5-A2 2· A2 2· A3 3-C1 2·A2 2·A2 2·A2 3=120-24-48=48种.
总结:通过上述4个例题的设置与分析,要使学生理解“插空法解决不相邻问题”的应用方法,作为一线教师,就需要精心设计出具体而形象的问题,通过具体问题的解决,抽象问题的转化与迁移,再结合具体的这类问题的练习,使学生从数学本质上理解插空法的精髓.
【参考文献】
[1]刘胜林.例谈排列组合中的“不相邻”问题[J].数理化学习(高一二版),2014(4):35-37.
[2]樊友年.“插空法”应用系列[J].数学通报,1995(1):18-21.
