一类由欧氏度量和1形式定义的对偶平坦Finsler度量

桂然然, 刘 凤, 宋卫东

(安徽师范大学 数学计算机科学学院, 安徽 芜湖 241003)

1 引言与主要结果

对偶平坦[1]的Finsler度量在信息几何、 超弦理论及相对论等领域应用广泛. 沈忠民[2]将对偶平坦的概念推广到Finsler空间上, 并用一组偏微分方程刻画局部对偶平坦的Finsler度量, 即F=F(x,y)是U ⊂n上的Finsler度量, 则F是对偶平坦的当且仅当

[F2]xkylyk-2[F2]xl=0.

因此, 研究和构造对偶平坦的Finsler度量是Finsler几何中的一个重要问题. 目前, 已涌现许多对偶平坦Finsler度量[3-12], 例如: 单位球Bn⊂n上的Funk度量[3-4]

(1)

李本伶[5]根据Berwald度量[13-14]构造的对偶平坦Finsler度量

(2)

研究表明, Finsler度量(1),(2)均可视为欧氏度量|y|>、 内积〈x,y〉以及欧氏范数|x|>构成的度量. 周林峰[15]证明了任何球对称Finsler度量都可表示为|y|>,〈x,y〉和|x|>构成的度量. 本文考虑更一般的情形, 即由|y|>,〈x,y〉,|x|>,〈a,y〉和〈a,x〉构成的对偶平坦Finsler度量. 李本伶[5]构造了该类对偶平坦的Finsler度量:

(3)

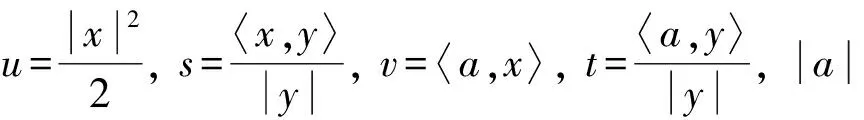
本文研究是否存在更多的由|y|>,〈x,y〉,|x|>,〈a,y〉和〈a,x〉构成的对偶平坦Finsler度量. 因此, 考虑下列Finsler度量：

(4)

其中:x∈n;y∈Txn;a为n上的任一常量;f为光滑函数. 本文给出Finsler度量(4)为对偶平坦的等价条件：

sfu s+tfv s+fs s-2fu=0,

(5)

sfu s+tfv t+fs t-2fv=0,

(6)

其中:

为找到更明确的度量, 本文考虑一种特殊情形下的解. 大多数例子如式(1)～(3)都满足ftt=0, 在该条件下, 可得以下结论:

定理2如果ftt=0, 则下列函数为方程(5)-(6)的解:

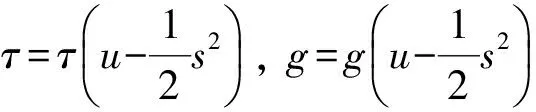
(7)

显然, 式(7)中f满足ftt=0. 根据定理1和定理2可得以下推论:

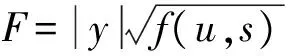
sfus+fss-2fu=0.

(8)

且对任意光滑函数g和θ, 方程(8)的解可表示为

2 预备知识

设M是一个n维的光滑实流形,TxM是x∈M处的切空间, 则TM∶=∪TxM={(x,y)|x∈M,y∈TxM}是M的切丛. 流形TM{0}称为带孔切丛, 其中{0}表示零截面.

设M是一个n维的光滑流形, 如果函数F∶=TM→[0,+∞)满足:

1) 正则性:F在TM{0}上是光滑函数;

2) 正齐性:F(x,λy)=λF(x,y), ∀λ>0;

3) 强凸性: 在TM{0}的任意局部坐标系(xi,yi)中,n×n矩阵(gij)是正定的, 其中

(9)

则称F是流形M上的Finsler度量. 具有Finsler度量的流形称为Finsler流形, 记作(M,F). 张量

g∶=gij(x,y)dxi⊗dxj

是切丛TM上的二阶正定对称协变张量, 称为F的基本张量.

在Finsler几何中, 测地系数

(10)

其中:

如果流形M上的Finsler度量F称为对偶平坦的, 则其在TM上任一点都存在局部坐标系(xi), 使得

其中H=H(x,y)是切丛TM上的一个标量函数.

引理1[2]设F(x,y)是开集U ⊂n上的一个Finsler度量, 则F是对偶平坦的当且仅当

[F2]xkylyk-2[F2]xl=0,

(11)

3 定理的证明

3.1 定理1的证明

直接计算可得

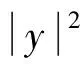
(12)

(13)

将式(12),(13)代入式(11), 可得

整理可得

(14)

令

A=sfus+tfvs+fss-2fu,B=sfut+tfvt+fst-2fv,

则式(14)可写为

(|y|>xl-syl)|y|>A+(|y|>al-tyl)|y|>B=0.

(15)

式(15)对任意的x,y都成立, 故可得A=0,B=0.

3.2 定理2的证明

由定理1可知

(sfu+tfv+fs)s-2fu=0,

(16)

(sfu+tfv+fs)t-2fv=0.

(17)

将式(16),(17)分别求关于t和s的微分, 可得

由式(18),(19), 可得

fut=fvs.

(20)

假设ftt=0, 令

f∶=φ(u,s,v)t+ψ(u,s,v).

(21)

将式(21)代入式(20), 可得

φu=φsvt+ψsv.

(22)

又φ,ψ与变量t无关, 故由式(22)可得

φsv=0,

(23)

φu=ψsv.

(24)

将式(21)代入式(16), 有

t2φsv+t(sφus+φss+ψsv-2φu)+sψus+ψss-2ψu=0.

(25)

再由式(23),(24), 可将式(25)化简为

t(sφus+φss-φu)+sψus+ψss-2ψu=0.

(26)

式(26)对任意的t都成立, 则式(26)等价于

sφus+φss-φu=0,

(27)

sψus+ψss-2ψu=0.

(28)

再将式(21)代入式(17), 有

(sφu+φs-2ψv)-tφv=0.

同理, 有

φv=0,

(29)

sφu+φs-2ψv=0.

(30)

根据式(29), 可将φ定义为

φ=φ(u,s).

(31)

考虑如下的变量替换：

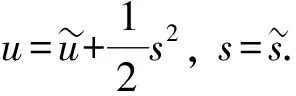
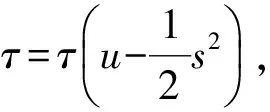
(32)

其中h=h(u)是关于u的光滑函数. 对式(30)求关于u和s的微分, 分别为

将式(33),(34)代入式(18), 可得

(35)

因此存在一个光滑函数ω=ω(u,x), 使得

(36)

下面确定ω=ω(u,x), 对式(36)直接计算可得

将式(37)～(39)代入式(28)中, 有

sωus+ωss-2ωu=0.

(40)

求方程(40)关于s的微分, 得

sωuss+ωsss-ωus=0.

(41)

令ξ∶=ωs, 则式(41)可写为

sξus+ξss-ξu=0.

(42)

显然ξ满足

(43)

其中ρ=ρ(u)是关于u的光滑函数. 故由ξ=ωs可知, 存在光滑函数θ=θ(u), 使得

(44)

对式(44)直接计算, 有

再将式(45)～(47)代入式(40), 可得

ρ(u)=2θ′(u).

则ω可写为

(48)

根据式(48), 有

(49)

将式(32),(49)代入式(21), 可得

证毕.

[1] Amari S, Nagaoka H. Methods of Information Geometry [M]. Providence, RI: American Mathematical Society, 2007.

[2] SHEN Zhongmin. Riemann-Finsler Geometry with Applications to Information Geometry [J]. Chinese Annals of Mathematics (Series B), 2006, 27(1): 73-94.

[3] Funk P. Über Geometrien bei Denen die Geraden die Kürtzesten Sind [J]. Mathematische Annalen, 1929, 101(1): 226-237.

[4] Funk P. Über Zweidimensionable Finslersche Räume, Insbesondere Über Solche Mit Geradlinlgen Extremalen und Positiver Konstanter Krümmung [J]. Mathematische Zeitschrift, 1936, 40(1): 86-93.

[5] LI Benling. On Dually Flat Finsler Metrics [J]. Differential Geometry and Its Applications, 2013, 31(6): 718-724.

[6] XIA Qiaoling. On Locally Dually Flat (α,β)-Metrics [J]. Differential Geometry and Its Applications, 2011, 29(2): 233-243.

[7] YU Changtao. On Dually Flat General (α,β)-Metrics [J]. Differential Geometry and Its Applications, 2015, 40: 111-122.

[8] HUANG Libing, MO Xiaohuan. On Some Explicit Constructions of Dually Flat Finsler Metrics [J]. Journal of Mathematical Analysis and Applications, 2013, 405(2): 565-573.

[9] CHENG Xinyue, SHEN Zhongmin, ZHOU Yusheng. On Locally Dually Flat Finsler Metrics [J]. International Journal of Mathematics, 2010, 21(11): 1531-1543.

[10] CHENG Xinyue, TIAN Yanfang. Locally Dually Flat Finsler Metrics with Special Curvature Properties [J]. Differential Geometry and Its Applications, 2011, 29(1): 98-106.

[11] XIA Qiaoling. On a Class of Locally Dually Flat Finsler Metrics of Scalar Flag Curvature [J]. Publicationes Mathematicae Debrecen, 2011, 78(1): 169-190.

[12] YU Changtao. On Dually Flat Randers Metrics [J]. Nonlinear Analysis: Theory, Methods & Applications, 2014, 95: 146-155.

[13] Berwald L. Über dien-Dimensionalen Geometrien Konstanter Krümmung, in Denen die Geraden die Kürzesten Sind [J]. Mathematische Zeitschrift, 1929, 30(1): 449-469.

[14] Berwald L. Über Eine Charakteristiche Eigenschaft der Allgemeinen Räume Konstanter Krümmung Mit Geradlinigen Extremalen [J]. Monatshefte für Mathematik und Physik, 1929, 36(1): 315-330.

[15] ZHOU Linfeng. Spherically Symmetric Finsler Metric inn[J]. Publicationes Mathematicae Debrecen, 2012, 80(1/2): 67-77.