基于粒子群协同优化算法的供应链金融信用风险评价模型

刘 颖, 张丽娟, 韩亚男, 庞丽艳, 王 帅,

(1. 吉林财经大学 管理科学与信息工程学院, 长春 130117; 2. 吉林省物流产业经济与智能物流重点实验室, 长春 130117;3. 吉林财经大学 互联网金融重点实验室, 长春 130117; 4. 长春工业大学 计算机科学与工程学院, 长春 130012； 5. 长春工业大学 马克思主义学院， 长春 130012)

供应链金融是大数据、 云计算、 互联网技术与传统金融业高度融合的金融产物[1]. 与传统融资模式相比, 供应链融资包含的资金关系错综复杂, 评估指标动态多样, 使得供应链融资的风险及风险评价有其自身的特征及难度[2].

目前, 金融风险评价方法主要包括Logistic模型[3]、 决策树方法[4]和神经网络方法[5]等. 支持向量机(support vector machines, SVM)是机器学习的一种经典方法, 具有结构简单, 泛化能力强, 易解决具有高维特征、 小样本与不确定性等问题的优势[6]. 目前已将支持向量机技术应用于信用风险度量[7-9]. 支持向量机分类器能克服人工神经网络局部极值的不足, 解决了传统统计方法所要求的向量服从正态分布的问题. 支持向量机分类模型中核函数和惩罚参数是决定分类器泛化能力的主要因素. 针对SVM参数优化问题, 利用网格法[10]和智能优化算法对SVM参数进行优化[11]取得了较好的分类效果. 此外, 供应链融资企业评估特征的相关性强、 冗余度高等特点使特征提取成为风险评估的重要前提, 其直接影响风险度量的速度与精度. Liang等[12]利用特征选择方法解决财务预警问题; 朱颢东等[13]提出了利用并行二进制免疫量子粒子群优化算法, 可较快获得具有代表性的特征子集； 陈仕涛等[14]在邻域粗糙集基础上构造粒子群算法的适应度函数, 提出了基于邻域粗糙集模型和粒子群优化的特征选择算法.

本文以传统融资模式下的信用风险评价指标为基础, 通过剖析供应链金融模式下信用风险度量指标, 构建群协同优化SVM信用风险评估模型, 利用二进制粒子群算法实现特征属性的选择和SVM关键参数的同步优化, 克服了高维特征属性和分类器参数对分类模型的影响, 获得了分类性能较高的SVM评估方法.

1 模型算法

1.1 SVM算法

SVM是一种基于结构风险最小化原理的模式识别方法, 它将样本点映射到高维特征空间, 使得正例和反例之间边缘最大化, 以获得最优化分类超平面, 分类超平面可表示为

f(x)=(w·x+b),

(1)

其中：w表示可调的权值向量;b表示偏置. 归一化后, 使得对线性可分样本集合(xi,yi),xi∈n,n是样本数量,yi∈{+1,-1}(i=1,2,…,n), 满足：

yi(〈w·xi〉+b)≥1, 1≤i≤n.

(2)

非线性情况下, 分类超平面w·φ(x)+b=0,φ(x)是非线性映射函数, 增加松弛变量ξi,ξi≥0表示为

yi(〈w,φ(xi)〉+b)≥1-ξi, 1≤i≤n.

(3)

求最优分类超平面表示为

(4)

其中c为惩罚系数, 其取值与错误分类样本惩罚程度成正比, 主要控制对错误判别样本的惩罚程度.

下面利用Lagrange优化方法把最优分类面问题转化为不等式约束下的二次函数寻优问题, 公式如下：

(5)

(6)

SVM引入核函数K(xi,xj)代替高维空间中的内积, 公式如下：

(7)

1.2 粒子群优化算法

粒子群优化(particle swarm optimization, PSO)算法是模拟鸟群捕食行为提出的一种智能算法. PSO算法的工作原理： 首先, 初始化为一组随机解, 通过迭代跟踪两个极值完成自我更新, 包括局部极值点(用Pid表示其位置)和全局极值点(用Pgd表示其位置); 然后在每轮迭代中, 粒子通过

更新自己的速度和位置. 其中：Xi=(Xi1,Xi2,…,Xid)表示粒子集;Vi=(Vi1,Vi2,…,Vid)表示在空间的飞行速度;d=1,2,…,D;ω表示惯性系数；c1和c2表示加速系数, 也称学习因子；r1,r2表示[0,1]的随机数. 迭代终止条件可设置为最大迭代次数或最小错误阈值.

传统PSO算法可解决连续优化问题, 为了使传统PSO算法更好地解决离散优化问题, Eberhart等[15]提出了离散PSO算法, 也称二进制PSO算法. 该算法在所提模型中将每一维Xid和Pid限制为1或0, 速度不作限制. 用速度更新位置, 如果Vid较高, 则粒子Xid选择1, 若Vid较低则Xid选0, 阈值在[0,1]之间. 供应链金融特征子集采用离散型PSO算法, 利用Sigmoid函数

(10)

2 特征选择与分类器参数协同优化模型

2.1 供应链金融风险评价指标体系

供应链金融模式是物流演变至供应链时期的一种物流金融形态, 供应链各方保持契约合作关系. 相对于传统的授信方式, 其融资模式强调互利性, 以对物流和资金流的动态控制代替对财务报表的静态分析, 淡化财务分析和准入控制, 从而规避了融资障碍. 银行对供应链成员评估综合宏观环境、 融资主体的中小企业、 业务往来的供应链核心企业、 供应链状况等一系列因素. 本文根据供应链融资模式的特点构建评价指标体系, 分为3个一级指标(F1～F3), 14个二级指标(S1～S14)和41个三级指标(T1～T41), 分别如图1～图3所示, 其中融资企业自身财务状况(T1～T21)作为传统信用风险评估指标, 融资企业、 核心企业、 供应链状况(T1～T41)作为供应链金融信用风险评估指标.

1) 供应链融资企业信用风险特征指标集如图1所示.

图1 供应链融资企业评价特征子集Fig.1 Feature subset of evaluation of supply chain financing enterprises

2) 供应链核心企业信用风险特征指标集如图2所示.

3) 融资企业产品供应链绩效评价特征指标集如图3所示.

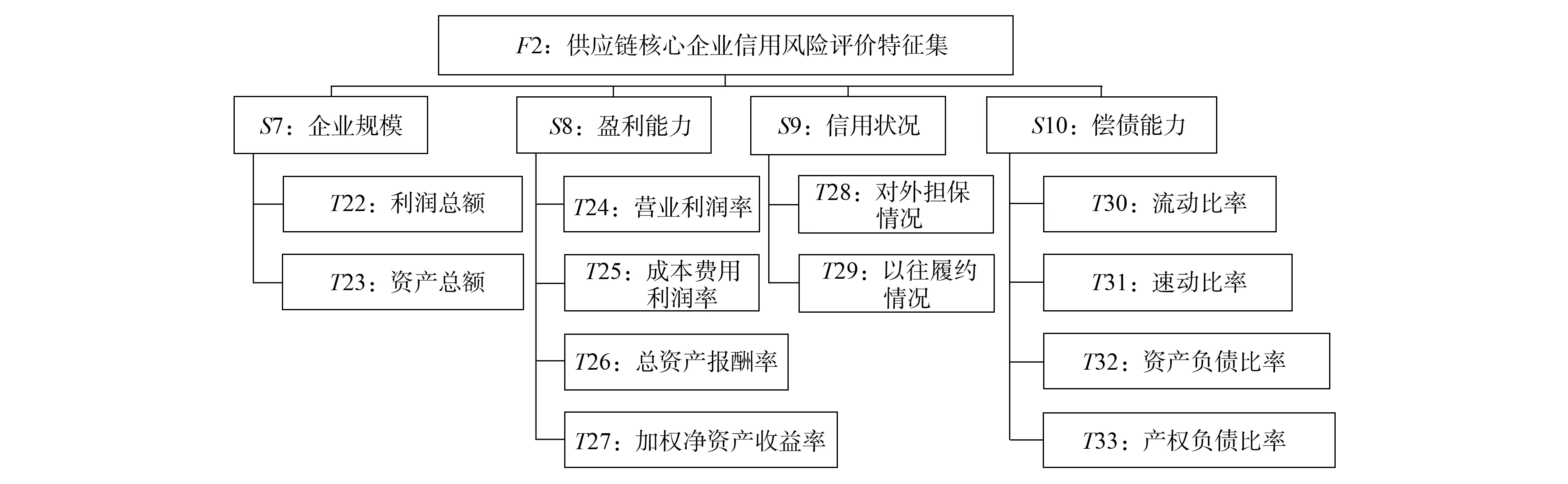
图2 供应链核心企业评价特征子集Fig.2 Feature subset of evaluation of supply chain core enterprises

图3 供应链绩效评价特征子集Fig.3 Feature subset of supply chain performance evaluation

2.2 算法描述

基于上述研究可见, 供应链金融模式下参与风险评价指标既包含定量指标也包含定性指标, 数量较多, 且属性之间相关性强, 冗余度高, 这些必然会降低评价模型的分类精度和速度. 评价模型必须尽可能保留信息含量大的指标, 剔除冗余的、 有噪声的属性值, 以降低分类的计算复杂度, 进而提高模型分类精度. 本节利用二进制PSO算法进行评价指标选择和SVM参数协同优化, 构建供应链金融风险评价模型(BPSO-SVM).

2.2.1 适应度函数的确定 通过SVM分类器的分类性能评价所选指标的有效性, 即以分类器的分类精度作为评价标准. 利用二进制PSO算法协同优化评价指标集合和SVM参数, 以评价函数估算评价指标集合和SVM参数的质量, 将最优的评价指标集合和SVM参数作为寻优结果输出.

图4 特征子集和SVM参数的粒子表示Fig.4 Feature subset and particle representation of SVM parameters

2.2.2 粒子编码方案 粒子涵盖两部分, 分别是特征向量和SVM参数值. 特征选择核心是从A个属性中选取B个属性值构成属性的子集合(B≤A). 因此, 粒子第一部分编码采用离散二进制变量,A个属性分别对应A维二进制空间. 对于每个粒子, 如果第i位为1, 则表示第i个属性被选中； 如果为0, 则表示该属性未被选中. 例如粒子K=(1100010001)表示10个属性中, 被选中的属性为1,2,6,10, 其余属性未被选中. 粒子第二部分为SVM的核参数, 本文选用径向基核函数, 参数包括核函数参数g, 惩罚参数c, 利用连续PSO算法优化得到. 在迭代过程中, 离散PSO算法和连续PSO算法产生不同的信用特征子集和参数值, 算法以SVM分类精度为评价准则, 当精度最高时所得的特征子集和SVM参数即为所求, 粒子编码方案如图4所示.

2.2.3 算法实现过程

1) 初始化粒子群, 每个粒子由信用特征子集、 惩罚参数c和核函数参数g三部分组成, 初始化粒子群参数, 包括设置学习因子、 粒子长度、 最大循环次数等；

2) 初始化粒子群速度；

3) 根据粒子编码方案将每个粒子各部分的值转化为对应选择的信用特征子集掩码, 并获取参数值, 根据所选特征子集和参数值计算每个粒子的适应度；

4) 根据粒子适应度的值更新Pi和Pg；

5) 根据式(8),(9)更新粒子的速度Vi和位置Xi；

6) 若迭代达到最大迭代次数, 则转7)； 否则, 返回3)继续迭代；

7) 输出当前最优的特征子集、 参数c,g及分类精度.

3 实验结果与比较

3.1 样本集描述

目前, 供应链金融业务主要集中在能源、 通信、 钢铁和汽车领域, 其中以汽车行业为典型供应链组织结构. 因此, 本文选择汽车制造业作为研究对象, 其结构分为上游(汽车零部件生产)、 中游(汽车制造)和下游(汽车销售)三部分. 以汽车制造企业为核心企业, 并选择汽车软件业、 五金、 发动机制造为上游企业及汽车销售与售后为下游企业, 经分析筛查认定“信用良好”和“信用不良”共计60家企业, 296个样本, 其中以某些因财务状况异常而被“特殊处理”(special treatment, ST)企业作为信用不良样本, 训练样本的类别和数量列于表1.

表1 训练样本的类别和数量

3.2 参数设置

实验参数设置如下： 学习因子c1=2,c2=2; 数据维数为43, 其中前41维用二进制表示信用特征向量, 后2维分别用十进制表示参数c和g的值； 迭代次数dmax=300, 即迭代300次算法停止运行； 粒子数目group=20.

3.3 SVM不同核函数对分类精度的影响

由SVM理论可知, SVM通过引入核函数实现高维空间的内积运算, 进而解决非线性分类. 核函数的选择通常包括核函数类型的选择与核函数相关参数的选择. SVM分类模型通常包含以下几种常用的核函数：

1) 径向基核函数(RBF)：K(xi,x)=exp{-γ‖xi-x‖2}；

2) 线性核函数(linear)：K(xi,x)=(xi·x)；

3) Sigmoid核函数：K(xi,x)=tanh(v(xi·x)+c)；

4) 多项式核函数(polynomial):K(xi,x)=(xi·x+1)d.

本文利用样本集对比SVM的4种核函数分类精度差异, 其对应的核函数参数选择默认值, 结果列于表2.

表2 SVM的4种核函数精度比较

由表2可见, 使用SVM-RBF方法分类的精度明显高于其他3种核函数方法, 其中SVM-polynomial 分类精度(66.10%)最低, SVM-RBF方法得到的分类精度比SVM-Sigmoid和SVM-linear方法分别高出3.39%和13.56%.

3.4 特征选择和参数优化前后的评价比较

为了验证所给模型的性能, 本文进行如下实验：

1) 比较传统径向基SVM(SVM-RBF), 利用主成分分析(PCA)特征提取(PCA-SVM-RBF)和二进制PSO特征提取及参数协同优化(BPSO-SVM-RBF)3个分类模型的分类性能；

2) 为说明供应链金融模式下特征属性对模型影响的程度, 实验分别将传统信用风险评估指标体系与供应链金融信用风险评估指标体系进行分类比较.

KMO和Bartlett检验结果列于表3. 由表3可见, KMO检测结果为0.796, 大于适合因子分析最低值0.6; 同时, Bartlett球形检验显著性水平值为0(<0.01), 以上结果均显示该组数据适合主成份提取. 根据解释的总方差, 选取特征值大于1作为主成分, 对于传统信用风险评估指标体系有6个主成分, 针对供应链金融信用风险评估指标体系, 包括11个主成分. 3种评价模型在不同评估指标体系中的比较结果列于表4. 由表4可见： 所得PCA-SVM-RBF模型相比于SVM-RBF模型在分类器参数默认情况下(c=1,g=0.5), 分类精度有所提升, 由84.75%提高至86.94%. 而BPSO-SVM-RBF利用二进制PSO进行特征选择, 得到二进制掩码为“1”的个数是9, 优选后特征数从原来的41个减少为9个. 特征选择的同时利用BPSO-SVM对SVM参数c和g的值进行优化, 分别得到惩罚参数54.42和核函数参数值0.1, 所得分类精度从PCA-SVM-RBF的86.94%, SVM-RBF的84.57%提高至91.43%, 表明SVM分类器参数的取值对分类精度有很大影响. 此外, 冗余特征在一定程度上干扰分类器性能, 采用二进制PSO算法选取特征值优于传统的PCA降维方法.

表3 KMO和Bartlett检验

表4 3种评价模型在不同评估指标体系中的比较

对3个模型分别对供应链金融信用风险评估指标体系与传统信用风险评估指标体系进行评估实验. 传统信用风险评估指标体系所讨论的供应链融资企业自身信用风险特征指标集, 共21个特征属性(T1～T21). 对比可见, BPSO-SVM-RBF使用传统信用风险评估指标体系分类精度为81.71%, 而BPSO-SVM-RBF使用供应链金融信用风险评估指标体系分类精度为91.43%, 精度提高9.72%. 同时, SVM-RBF与PCA-SVM-RBF模型分类精度均有提升, 分别提高6.32%和6.78%. 实验结果表明, 供应链金融信用风险评估指标体系有助于提高分类器的整体性能.

综上所述, 本文一方面从供应链融资企业本身、 供应链核心企业和融资企业产品供应链绩效3个角度提出了评价指标体系； 另一方面提出了种群协同优化信用风险评价模型(BPSO-SVM), 利用二进制粒子群算法实现特征属性的选择和SVM关键参数同步优化, 有效解决了高维、 冗余的特征属性和不准确分类器参数对分类模型的影响. 实验结果表明, 本文提出的基于群协同优化算法的风险评估模型在解决供应链金融信用风险评价问题中具有较好的性能.

[1] 熊熊, 马佳, 赵文杰, 等. 供应链金融模式下的信用风险评价 [J]. 南开管理评论, 2009, 12(4): 92-98. (XIONG Xiong, MA Jia, ZHAO Wenjie, et al. Credit Risk Analysis of Supply Chain Finance [J]. Nankai Business Review, 2009, 12(4): 92-98.)

[2] 于辉, 王亚文. 供应链金融视角下利率市场化的鲁棒分析模型 [J]. 中国管理科学, 2016(2): 19-26. (YU Hui, WANG Yawen. The Robust Model of Interest Rates Iberalization from Supply Chain Finance Perspective [J]. Chinese Journal of Management Science, 2016(2): 19-26.)

[3] You J S, Ando T. A Statistical Modeling Methodology for the Analysis of Term Structure of Credit Risk and Its Dependency [J]. Expert Systems with Applications, 2013, 40(12): 4897-4905.

[4] Mandala G N N, Nawangpalupi C B, Praktikto F R. Assessing Credit Risk: An Application of Data Mining in a Rural Bank [J]. Procedia Economics and Finance, 2012, 4: 406-412.

[5] Erdal H, Ekinci A. A Comparison of Various Artificial Intelligence Methods in the Prediction of Bank Failures [J]. Computational Economics, 2013, 42(2): 199-215.

[6] ZHONG Haoming, MIAO Chunyan, SHEN Zhiqi, et al. Comparing the Learning Effectiveness of BP, ELM, I-ELM, and SVM for Corporate Credit Ratings [J]. Neurocomputing, 2014, 128: 285-295.

[7] Danenas P, Garsva G. Selection of Support Vector Machines Based Classifiers for Credit Risk Domain [J]. Expert System with Application, 2015, 42(6): 3194-3204.

[8] Harris T. Credit Scoring Using the Clustered Support Vector Machine [J]. Expert Systems with Applications, 2015, 42(2): 741-750.

[9] 薛飞, 鲁利民, 王磊. 新型光滑正则半监督SVM方法及其在信用评级中的应用 [J]. 计算机科学, 2013, 40(10): 239-242. (XUE Fei, LU Limin, WANG Lei. Novel Smooth Regularization Based Semi-supervised SVM Approach and Its Application in Credit Evaluation [J]. Computer Science, 2013, 40(10): 239-242.)

[10] LaValle S M, Branicky M S. On the Relationship between Classical Grid Search and Probabilistic Roadmaps [J]. International Journal of Robotics Research, 2002, 23(8): 673-692.

[11] LIU Ying, ZHANG Bai, HUANG Lihua, et al. A Novel Optimization Parameters of Support Vector Machines Model for the Land Use/Cover Classification [J]. International Journal of Food, Agriculture & Environment, 2012, 10(2): 1098-1104.

[12] Liang D, Tsai C F, Wu H T. The Effect of Feature Selection on Financial Distress Prediction [J]. Knowledge-Based Systems, 2015, 73: 289-297.

[13] 朱颢东, 钟勇. 基于并行二进制免疫量子粒子群优化的特征选择方法 [J]. 控制与决策, 2010, 25(1): 53-58. (ZHU Haodong, ZHONG Yong. Feature Selection Method Based on PBIQPSO [J]. Control and Decision, 2010, 25(1): 53-58.)

[14] 陈仕涛, 陈国龙, 郭文忠, 等. 基于粒子群优化和邻域约简的入侵检测日志数据特征选择 [J]. 计算机研究与发展, 2010, 47(7): 1261-1267. (CHEN Shitao, CHEN Guolong, GUO Wenzhong, et al. Feature Selection of the Intrusion Detection Data Based on Particle Swarm Optimization and Neighborhood Reduction [J]. Journal of Computer Research and Development, 2010, 47(7): 1261-1267.)

[15] Eberhart R, Kennedy J. A New Optimizer Using Particle Swarm Theory [C]//Proceedings of IEEE the Sixth International Symposium on Micro Machine and Human Science. Piscataway, NJ: IEEE, 1995: 39-43.