三模系统二阶非线性诱导的非传统光子阻塞

辛春雨, 马宏源, 孟书生, 王 野

(1. 白城师范学院 物理与电子信息学院, 吉林 白城 137000； 2. 郑州科技学院 基础部, 郑州 450064)

单光子在量子信息和量子通讯等领域应用广泛[1-2]. 当可实现单光子源的系统被经典场驱动时, 在原子腔系统中产生子Poisson光, 即光子阻塞效应[3-8]. 在光子阻塞现象中, 仅当腔中的光子离开腔后下一个光子才会产生. 为实现光子阻塞效应, 要求系统中的非线性要远大于系统的衰减率. 通过三阶非线性(Kerr非线性)系统可实现光子阻塞. 光子阻塞可应用于单光子晶体管[9]、 干涉仪[10]和量子光学二极管[11]中. 文献[12]提出了一种新的机制实现光子阻塞, 在该机制下, 实现强光子反聚束仅要求系统的非线性强度远小于系统的衰减率, 其机制为不同驱动耗散路径间的量子干涉[13-19].

文献[20-23]研究了三模二阶非线性系统中的非传统光子阻塞, 当3个模式a,b,c的频率关系为2ωa=2ωb=ωc时, 该系统中可发生非传统光子阻塞. 本文通过假设3个模式a,b,c的频率关系为ωa=ωb=2ωc, 推导一个新的Hamilton量, 并解析和数值研究该系统的非传统光子阻塞.

1 模 型

根据文献[22]推导一个Hamilton量. 由介电材料对电场的非线性反馈可得

(1)

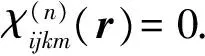
(2)

且

进行归一化. 能量密度的经典表达式为

(3)

其中:

(4)

系统总的Hamilton量为

(5)

其中：Fb(Fc)和φb(φc)分别表示对模b(模c)的驱动场强度和相位；ωL为驱动频率.

为方便, 对系统进行框架旋转. 定义算符

则相应的旋转操作为

在该操作下可得

(6)

其中Δi=2ωi-2ωL(i=a,b),Δc=ωc-ωL分别表示模a,b,c与驱动激光间的失谐. 由于ωa=ωb=2ωc, 因此失谐间的关系满足Δa=Δb=2Δc. 系统密度矩阵的演化由主方程支配, 主方程的形式为

其中κa,κb,κc分别表示模a,b,c的衰减率. 超算符定义为

不失一般性, 假设3个模式的衰减率相等, 即κa=κb=κc=κ. 光子的统计性质由稳态下的零时二阶关联函数描述, 定义为

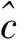
2 物理机制

本文考虑模c的光子阻塞, 其机制为不同路径间光的量子干涉. 系统的能级结构及跃迁路径[14]如图1所示. 由图1可见, 模c的双光子激发共有3条跃迁路径：

图1 系统的能级结构及跃迁路径Fig.1 Energy level structures and transition paths of system

1) 直接输入两光子至模c,

2) 在模b上激发一个光子, 且该光子通过二阶非线性交换至模c, 即

；

3) 模b中产生一个光子, 该光子先线性交换至模a, 再通过二阶非线性交换至模c, 即

当满足阻塞条件时, 3条路径上的光子到达模c时干涉相消, 干涉的结果为光子不能占据态|002〉. 当J=0时, 干涉路径变为两条, 当J≠0时,J的变化可改变φ的定义域.

3 解析和数值结果

[14]方法求解系统发生非传统光子阻塞的最佳条件. 设计系统的态被截断为

|ψ〉=C000|000〉+C100|100〉+C010|010〉+C001|001〉+C002|002〉,

(7)

其中|mnp〉表示系统的Fock态基,m,n,p分别表示模a,b,c上的光子数.

模损失可用非厄米Hamilton方法进行处理

可得一组系数耦合方程. 在弱驱动条件下F≪κ, 有|C000|>≫|C100|>,|C010|>,|C001|>≫|C002|>成立, 系统的稳态解Cmnp可通过解耦合方程得到. 若假设g1=g2=g, 则

(8)

考虑模c上发生强的光子反聚束, 令系数C002=0, 则可得发生光子反聚束的最佳条件为

(9)

(10)

当式(9)和式(10)同时满足时, 光子阻塞才会发生. 在Kerr非线性系统中, 两个驱动强度的相位差包含于阻塞条件中, 由于非线性形式不同, 因此阻塞条件仅与对模b的驱动相位φb有关. 为方便, 令φb=φ, 将式(9)和式(10)分别变为

(11)

(12)

当满足式(11)和式(12)时, 光子不能占据态|002〉.

为描述非传统光子阻塞效应, 在一个截断的Hilbert空间中求解主方程, 当J/κ取不同值时, 二阶关联函数g(2)(0)随二阶非线性系数g/κ和驱动φ的变化如图2所示, 其中Hilbert空间截断为模a3维、 模b3维和模c6维, 其参数为Fb/κ=Fc/κ=0.1,Δ值由方程组(11)和(12)的第一个方程决定. 图2中虚线表示由方程组(11)和(12)中第二个方程计算的解析解, 白色虚线表示发生阻塞的解析解, 与白色虚线对应的深色区域表示由数值解主方程得到的精确数值解. 由图2可见, 解析解和数值解相符. 由方程组(11)和(12)可见, 当满足

κ2cos2(φ)+4(J2-2κ2)sin2(φ)+6Jκsin(2φ)≥0

(13)

时, 将发生光子阻塞. 由解析解和数值解可见, 阻塞区域的周期为2π. 当参数J/κ=4时, 对应的阻塞区域类似多个封闭三角形, 且φ的取值在某些范围内阻塞不会发生. 当J/κ=20时, 阻塞区域类似正弦曲线, 阻塞区域变大, 即J/κ发生变化可引起阻塞区域的变化, 当J/κ足够大时,φ趋于连续.

综上, 本文研究了三模二阶非线性系统中由弱二阶非线性引起的非传统光子阻塞. 通过计算主方程的稳态解及二阶关联函数可见, 强光子反聚束可被驱动场的相位和线性耦合强度控制, 且用非厄米Hamilton方法求得最佳光子阻塞条件与精确的数值模拟结果相符.

参考文献

[2] 查嫽, 曹怀信, 王晓霞. 量子信道对纠缠鲁棒性的影响 [J]. 吉林大学学报(理学版), 2016, 54(4): 871-877. (ZHA Liao, CAO Huaixin, WANG Xiaoxia. Influences of Quantum Channels on Robustness of Entanglement [J]. Journal of Jilin University (Science Edition), 2016, 54(4): 871-877.)

[3] Imamoglu A, Schmidt H, Woods G, et al. Strongly Interacting Photons in a Nonlinear Cavity [J]. Phys Rev Lett, 1997, 79(8): 1467-1470.

[4] Miranowicz A, Paprzycka M, LIU Yuxi, et al. Two-Photon and Three-Photon Blockades in Driven Nonlinear Systems [J]. Phys Rev A, 2013, 87(2): 023809.

[5] Birnbaum K M, Boca A, Miller R, et al. Photon Blockade in an Optical Cavity with One Trapped Atom [J]. Nature, 2005, 436: 87-90.

[6] Faraon A, Fushman I, Englund D, et al. Coherent Generation of Non-classical Light on a Chip via Photon-Induced Tunnelling and Blockade [J]. Nat Phys, 2008, 4(11): 859-863.

[7] Hoffman A J, Srinivasan S J, Schmidt S, et al. Dispersive Photon Blockade in a Superconducting Circuit [J]. Phys Rev Lett, 2011, 107(5): 053602.

[8] LIU Yuxi, XU Xunwei, Miranowicz A, et al. From Blockade to Transparency: Controllable Photon Transmission through a Circuit-QED System [J]. Phys Rev A, 2014, 89(4): 043818.

[9] Chang D E, Sørensen A S, Demler E A, et al. A Single-Photon Transistor Using Nanoscale Surface Plasmons [J]. Nat Phys, 2007, 3(11): 807-812.

[11] Shen H Z, Zhou Y H, Yi X X. Quantum Optical Diode with Semiconductor Microcavities [J]. Phys Rev A, 2014, 90(2): 023849.

[12] Liew T C H, Savona V. Single Photons from Coupled Quantum Modes [J]. Phys Rev Lett, 2010, 104(18): 183601.

[13] Carmichael H J. Photon Antibunching and Squeezing for a Single Atom in a Resonant Cavity [J]. Phys Rev Lett, 1985, 55(25): 2790-2793.

[15] XU Xunwei, LI Yong. Tunable Photon Statistics in Weakly Nonlinear Photonic Molecules [J]. Phys Rev A, 2014, 90(4): 043822.

[16] XU Xunwei, LI Yong. Strong Photon Antibunching of Symmetric and Antisymmetric Modes in Weakly Nonlinear Photonic Molecules [J]. Phys Rev A, 2014, 90(3): 033809.

[17] Ferretti S, Savona V, Gerace D. Optimal Antibunching in Passive Photonic Devices Based on Coupled Nonlinear Resonators [J]. New J Phys, 2013, 15(2): 025012.

[18] XU Xunwei, LI Yuanjie. Antibunching Photons in a Cavity Coupled to an Optomechanical System [J]. J Phys B: At Mol Opt Phys, 2013, 46(3): 035502.

[19] Majumdar A, Bajcsy M, Rundquist A, et al. Loss-Enabled Sub-Poissonian Light Generation in a Bimodal Nanocavity [J]. Phys Rev Lett, 2012, 108(18): 183601.

[20] Shen H Z, Zhou Y H, Yi X X. Tunable Photon Blockade in Coupled Semiconductor Cavities [J]. Phys Rev A, 2015, 91(6): 063808.

[21] Zhou Y H, Shen H Z, Yi X X. Unconventional Photon Blockade with Second-Order Nonlinearity [J]. Phys Rev A, 2015, 92(2): 023838.

[22] Gerace D, Savona V. Unconventional Photon Blockade in Doubly Resonant Microcavities with Second-Order Nonlinearity [J]. Phys Rev A, 2014, 89(3): 031803.

[23] Zhou Y H, Shen H Z, Shao X Q, et al. Strong Photon Antibunching with Weak Second-Order Nonlinearity under Dissipation and Coherent Driving [J]. Opt Express, 2016, 24(15): 17332-17344.